3.1.1 一元一次方程课件
文档属性
| 名称 | 3.1.1 一元一次方程课件 |  | |
| 格式 | zip | ||
| 文件大小 | 581.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-23 13:49:27 | ||
图片预览






文档简介
课件17张PPT。3.1.1 一元一次方程3.1 从算式到方程
(第1课时) 3.1.1 一元一次方程教学目标:1. 理解方程、一元一次方程的定义。2. 能够找出等量关系,列出方程。教学重点:
一元一次方程的判断3.1.1 一元一次方程——教学流程问题:1.你能回想出方程定义吗? 先设字母表示未知数,然后根据问题中的相等关系,写出含有未知数的等式——方程. 方程是含有未知数的等式
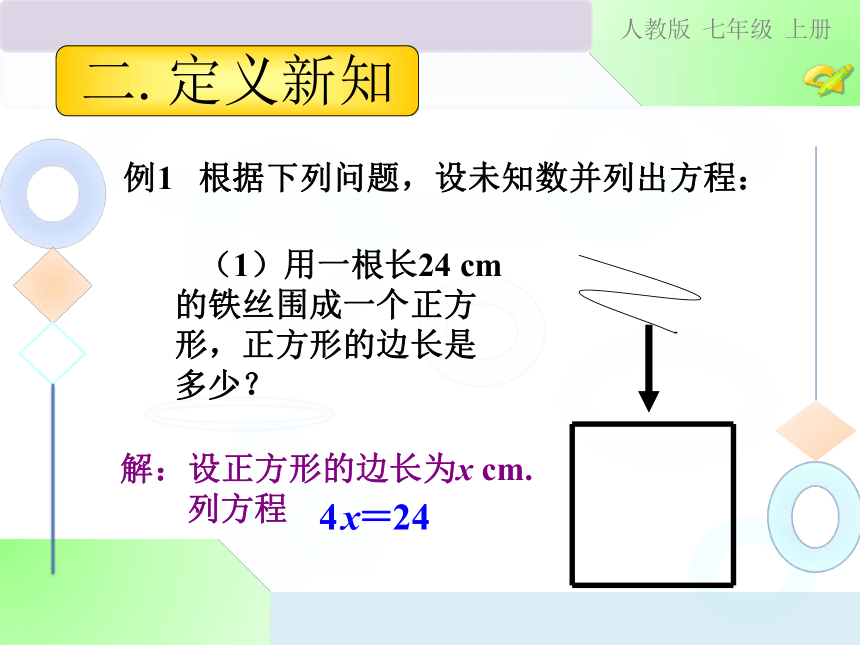
例如:2x=5 , 3x+1=4 , 5x-7=8 2.列方程的步骤:一.回顾旧知例1 根据下列问题,设未知数并列出方程: (1)用一根长24 cm的铁丝围成一个正方形,正方形的边长是多少? 解:设正方形的边长为x cm.
列方程 二.定义新知例1 根据下列问题,设未知数并列出方程: (2)一台计算机已使用1700 h,预计每月再使用150 h,经过多少月这台计算机的使用时间达到规定
的检修时间2450 h? 解: 设x月后这台计算机的使用时间达到2450 h,
那么在x月里这台计算机使用了150x h.
列方程例1 根据下列问题,设未知数并列出方程: (3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生? 解:设这个学校的学生数为x,那么女生数为0.52x,男生数为(1-0.52)x.
列方程问题:观察上面例题列出的三个方程有什么特征?(1)只含有一个未知数 x;(2)未知数x的指数都是1;(3)等号两边都是整式。 一元一次方程:
只含有一个未知数(元),未知数的次数都是1,等号两边都是整式 ,这样的方程叫做一元一次方程.1.下列式子哪些是方程,哪些是一元一次方程?
(1) ;(2) ;
(3) ;(4) ;
(5) ;(6) .解:(2)(3)(4)(5)是方程.(2)(3)是一元一次方程.三.练习巩固2. 归纳小结 巩固发展 请同学们回想例1中的三个小题,并回答下列问题:
(1)怎样将一个实际问题转化为方程问题?
(2)列方程的依据是什么? 实际问题设未知数列方程一元一次方程 (2)列方程的依据:分析实际问题中的数量关系,利用其中的相等关系列出方程。解:(1) 1.下列各式中,是方程的是( )
① ; ② ; ③ ;
④ ; ⑤ .
(A)①②③④⑤ (B)①③④⑤
(C)②③④⑤ (D)③④⑤
2.下列各式中,是一元一次方程的是( ).
(A) (B)
(C) (D)
DC四.目标检测3.根据下列问题,设未知数,列出方程,并指出是否为一元一次方程:
(1)环形跑道一周长400 m,沿跑道跑多少周,可以跑3 000 m?
(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
(3)一个梯形的下底比上底多2 cm,高是5 cm,面积是40 cm2,求上底.
(4)用买10 个大水杯的钱,可以买15 个小水杯,大水杯比小水杯的单价多5 元,两种水杯的单价各是多少元?3.根据下列问题,设未知数,列出方程,并指出是否为一元一次方程:
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3 000 m?
(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
解:(1)设沿跑道跑x周,(2)设甲种铅笔买了x支,乙种铅笔买了(20 - x)支,
是一元一次方程.是一元一次方程3.根据下列问题,设未知数,列出方程,并指出否为一元一次方程:
(3)一个梯形的下底比上底多2 cm,高是5 cm,面积是40 cm2,求上底.
(4)用买10个大水杯的钱,可以买15个小水杯,大水杯比小水杯的单价多5元,两种水杯的单价各是多少元?解:(3)设上底为x cm,
(4)设小水杯的单价是x 元,大水杯的单价是(x+5) 元,
是一元一次方程是一元一次方程(1)本节课学习了哪些主要内容?(2)一元一次方程的三个特征各指什么?(3)从实际问题中列出方程的关键是什么?五.课堂小结六.课后练习??谢谢!
(第1课时) 3.1.1 一元一次方程教学目标:1. 理解方程、一元一次方程的定义。2. 能够找出等量关系,列出方程。教学重点:
一元一次方程的判断3.1.1 一元一次方程——教学流程问题:1.你能回想出方程定义吗? 先设字母表示未知数,然后根据问题中的相等关系,写出含有未知数的等式——方程. 方程是含有未知数的等式
例如:2x=5 , 3x+1=4 , 5x-7=8 2.列方程的步骤:一.回顾旧知例1 根据下列问题,设未知数并列出方程: (1)用一根长24 cm的铁丝围成一个正方形,正方形的边长是多少? 解:设正方形的边长为x cm.
列方程 二.定义新知例1 根据下列问题,设未知数并列出方程: (2)一台计算机已使用1700 h,预计每月再使用150 h,经过多少月这台计算机的使用时间达到规定
的检修时间2450 h? 解: 设x月后这台计算机的使用时间达到2450 h,
那么在x月里这台计算机使用了150x h.
列方程例1 根据下列问题,设未知数并列出方程: (3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生? 解:设这个学校的学生数为x,那么女生数为0.52x,男生数为(1-0.52)x.
列方程问题:观察上面例题列出的三个方程有什么特征?(1)只含有一个未知数 x;(2)未知数x的指数都是1;(3)等号两边都是整式。 一元一次方程:
只含有一个未知数(元),未知数的次数都是1,等号两边都是整式 ,这样的方程叫做一元一次方程.1.下列式子哪些是方程,哪些是一元一次方程?
(1) ;(2) ;
(3) ;(4) ;
(5) ;(6) .解:(2)(3)(4)(5)是方程.(2)(3)是一元一次方程.三.练习巩固2. 归纳小结 巩固发展 请同学们回想例1中的三个小题,并回答下列问题:
(1)怎样将一个实际问题转化为方程问题?
(2)列方程的依据是什么? 实际问题设未知数列方程一元一次方程 (2)列方程的依据:分析实际问题中的数量关系,利用其中的相等关系列出方程。解:(1) 1.下列各式中,是方程的是( )
① ; ② ; ③ ;
④ ; ⑤ .
(A)①②③④⑤ (B)①③④⑤
(C)②③④⑤ (D)③④⑤
2.下列各式中,是一元一次方程的是( ).
(A) (B)
(C) (D)
DC四.目标检测3.根据下列问题,设未知数,列出方程,并指出是否为一元一次方程:
(1)环形跑道一周长400 m,沿跑道跑多少周,可以跑3 000 m?
(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
(3)一个梯形的下底比上底多2 cm,高是5 cm,面积是40 cm2,求上底.
(4)用买10 个大水杯的钱,可以买15 个小水杯,大水杯比小水杯的单价多5 元,两种水杯的单价各是多少元?3.根据下列问题,设未知数,列出方程,并指出是否为一元一次方程:
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3 000 m?
(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
解:(1)设沿跑道跑x周,(2)设甲种铅笔买了x支,乙种铅笔买了(20 - x)支,
是一元一次方程.是一元一次方程3.根据下列问题,设未知数,列出方程,并指出否为一元一次方程:
(3)一个梯形的下底比上底多2 cm,高是5 cm,面积是40 cm2,求上底.
(4)用买10个大水杯的钱,可以买15个小水杯,大水杯比小水杯的单价多5元,两种水杯的单价各是多少元?解:(3)设上底为x cm,
(4)设小水杯的单价是x 元,大水杯的单价是(x+5) 元,
是一元一次方程是一元一次方程(1)本节课学习了哪些主要内容?(2)一元一次方程的三个特征各指什么?(3)从实际问题中列出方程的关键是什么?五.课堂小结六.课后练习??谢谢!
