选择必修 第一章 1.1.2 空间向量的数量积运算 课件(共27张PPT)
文档属性
| 名称 | 选择必修 第一章 1.1.2 空间向量的数量积运算 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-18 10:34:49 | ||
图片预览








文档简介
(共27张PPT)
选择必修 第一章
1.1.2 空间向量的数量积运算
人教A版(2019)
教学目标
学习目标 数学素养
1.理解空间向量的夹角的概念. 1.空间抽象素养.
2.掌握空间向量数量积的概念、性质、计算方法及运算规律. 2.空间抽象素养和数学运算素养.
3.会用两个向量数量积解决立体几何中的一些简单的问题. 3.逻辑推理素养和数学运算素养.
温故知新
1.平面向量的夹角
2.平面向量的垂直
已知两个非零向量是平面是上的任意一点,作,则叫做向量与 的夹角.记作.
如果与的夹角是,我们就说与垂直,记作.
3.向量的投影向量
已知两个非零向量,它们的夹角为,我们把数量积叫做
向量与 的数量积(或内积),记作,即 .
规定:零向量与任一向量的数量积为0.
4.平面向量的数量积
如图,设是两个非零向量, 过的起点A和终点B,分别作所在直线的垂线,垂足分别为得到我们称上述变换为向量投影, 叫做向量上的投影向量.
新知探究
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以象平面向量那样来定义.
如图,已知两个非零向量a,b,在空间任取一点O、作=a,=b,则∠AOB叫做向量a,b的夹角,记作.
如果=,那么向量a,b互相垂直,记作a⊥b.
通常规定,
0≤≤π.这样,两个向量的夹角是唯一确定的,且=.
新知探究
已知两个非零向量a,b,则|a||b|cos叫做a,b的数量积(inner product),记作a·b.即
a·b=|a||b|cos.
结果为数值
特别地,零向量与任意向量的数量积为0.
由向量的数量积定义,可以得到:
a⊥b a b=0;
a·a= |a||a|cos=|a|2.
证明垂直
求长度
a·a也记作a2.
知新探究
在平面向量的学习中,我们学习了向量的投影,类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
如图, 在空间,向量a向向量b投影,由于它们是自由向量,因此可以将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,
.
向量c称为向量a在向量b上的投影向量.
知新探究
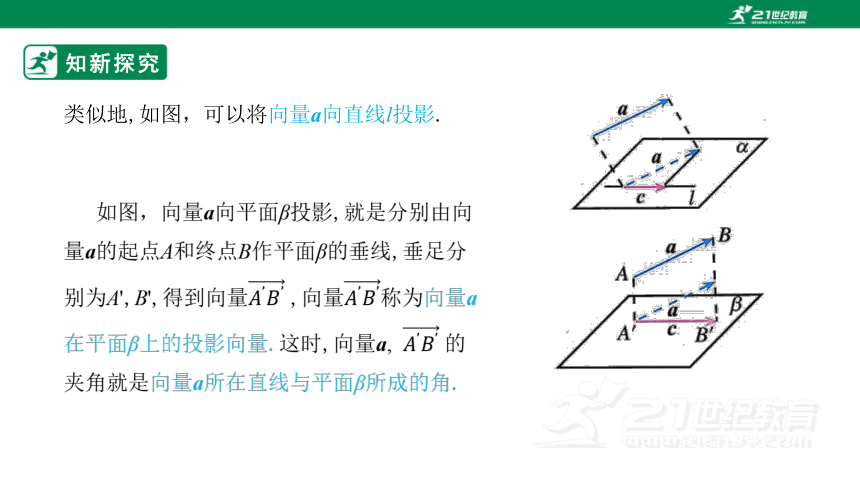
类似地,如图,可以将向量a向直线l投影.
如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量 ,向量称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
知新探究
空间向量数量积的运算律
(λa) b=λ(a b),λ∈R
a b=b a(交换律)
a (b+c)=a b+a c(分配律)
注意:数量积不满足结合律.
即(a b) c≠a (b c)
知新探究
1.对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量a,b,c,由a b=a c能得到b=c吗 如果不能,请举出反例.
2.对于三个均不为0的数a,b,c,若ab=c,则(或).对于向量a,b,若a·b=k,能否写成(或 )的形式
3.对于三个均不为0的数a,b,c,有(ab)c=a(bc).对于向量a,b,c,(a b)c=a(b c)成立吗 也就是说,向量的数量积满足结合律吗
1.对于三个向量,由 =不能得到=c.例如:如图所示,在长方体ABCD-中,向量与向量都垂
直,因此=0,显然, 不相等.
事实上,由 =得- =,进而得
,即向量与c垂直,但不一定有另外,当=0时,有 ==0,此时也不一定有.
知新探究
2.由,不能写成或的形式,即向量没有除法运算.向量有加法、减法、数乘和数量积运算,没有实数除以向量和向量除以向量的运算.
3.对于向量,c,()c= (b不成立,也就是说,向量数量积运算不满足结合律.
例如:任意取三个不共面的向量,c,其中,c不共线,(b是一个数与向量做数乘运算,()c是一个数与向量做数乘运算,而向量,c不共线,所以()c与(b不相等.
数量积的运算只满足交换律,分配律及数乘结合律,但不满足乘法结合律,即(a b)c不一定等于a(b c).这是由于(a b)c表示一个与c共线的向量,而
a(b c)表示一个与a共线的向量,而c与a不一定共线.
新知探究
【例1】如图,在正方体ABCD-A1B1C1D1中,求向量的夹角的大小.
解:
方法1:∵,
∵△D1AC为等边三角形,
∴,即,
分析:求两个向量的夹角,可以把其中一个向量平移到与另一个向量的起点重合,从而转化为求平面角的大小;也可以用两个向量的数量积定义a·b=|a||b|cos,求出cos =的值,然后确定的大小.
∴即为向量的夹角,
则向量的夹角为.
新知探究
【例1】如图,在正方体ABCD-A1B1C1D1中,求向量的夹角的大小.
解:
方法2:设正方体的棱长为1,则
又,,
=0+1+0+0=1
∴,
∵,
∴,
则向量的夹角为.
新知探究
两个非零向量夹角求法的两个途径:
1.转化求角:把向量夹角转化为平面几何中的对应角,利用解三角形的知识求解.
2.利用数量积求夹角:
⑴求向量数量积及向量的模;
⑵运用公式cos=利用数量积求向量夹角的余弦值;
⑶利用向量的夹角求分弦值,继而求角的大小.
注意:可以用非零向量夹角的求法,求异面直线所成的角.
①根据题设条件在所求的异面直线上取两个向量;
②异面直线所成角的问题转化为向量夹角问题.
初试身手
1.在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,AA1= ,求异面直线BA1与AC所成角的余弦值.
解:
∵,,
且0,AB=1
∴=-1
又,,
∴,
∵异面直线所成角的范围是(0,],
∴异面直线BA1与AC所成角的余弦值为.
新知探究
【例2】如图,在平行六面体ABCD-A'B'C'D中,AB=5,AD=3,AA'=7,∠BAD=60°,
∠BAA'=∠DAA'=45°.求:
⑴ ; ⑵AC'的长(精确到0.1).
解:
⑴
=7.5.
⑵
.
所以AC'≈13.3.
新知探究
利用空间向量求线段的长度或两点的距离:
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以向量的线性运算及数量积运算表示出来,因此立体几何中的许多问题可以用向量运算的方法加以解决.
⑴结合图形将所求线段用向量表示;
⑵用已知模和夹角的向量表示该向量;
⑶利用,通过计算求出,即得所求线段的长度或两点间的距离.
初试身手
2.如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又AB=4,AC=6,BD=8,求CD的长.
解:
∵CA AB,BD AB,
∴,
∵,且0,0,
∴
=68.
∴,即CD的长为.
新知探究
【例3】如图,m,n是平面α内的两条相交直线,直线l与α的交点为B,且l⊥m,l⊥n,求证:l⊥α.
分析:要证明l⊥α,就是要证明l垂直于α内的任意内的任意一条直线g(直线与平面垂直的定义).如果我们能在g和m,
n之间建立某种联系,并由l⊥m,l⊥n,得到l⊥g,那么就能解决此问题.
新知探究
【例3】如图,m,n是平面α内的两条相交直线,直线l与α的交点为B,且l⊥m,l⊥n,求证:l⊥α.
证明:
在平面α内作任意一条直线g,分别在直线l,m,n,g上取非零向量l,m,n,g.
由向量共面的充要条件可知,
存在唯一的有序买数对(x,y),使
将上式两边分别与向量l作数量积运算,得
因为l·m=0,l·n=0,所以l · g=0.
g=xm+yn.
所以l⊥g.
这就证明了直线l垂直于平面α内的任意一条直线,所以l⊥α.
因为直线m与n相交,所以向量m,n不平行.
l · g=xl·m+yl·n.
例3即为直线与平面垂直的判定定理的证明过程.尝试用综合几何证明这个定理,并比较两种方法,你能从中体会到向量方法的优越性吗?
初试身手
3.如图所示,在三棱锥中A-BCD,DA,DB,DC两两垂直,且DB=DC=DA=2,E为BC的中点.
⑴证明:AE⊥BC;
⑵求直线AE与DC所成角的余弦值.
⑴证明:∵DA,DB,DC两两垂直,
∴
=
==0.
又∵
,
∴,
则AE⊥BC.
初试身手
3.如图所示,在三棱锥中A-BCD,DA,DB,DC两两垂直,且DB=DC=DA=2,E为BC的中点.
⑴证明:AE⊥BC;
⑵求直线AE与DC所成角的余弦值.
⑵∵
解:
∴.
==2.
而.
=
则直线AE与DC所成角的余弦值为.
课堂小结
1.空间向量的夹角、数量积、投影向量
已知两个非零向量a,b,在空间任取一点O、作=a,=b,则∠AOB叫做向量a,b的夹角,记作
已知两个非零向量a,b,则|a||b|cos叫做a,b的数量积.即a·b=|a||b|cos.
.
如图,向量c称为向量a在向量b上的投影向量.
如图,可以将向量a向直线l投影.
如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量 ,向量称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
课堂小结
2.空间向量数量积的运算律
(λa) b=λ(a b),λ∈R
a b=b a(交换律)
a (b+c)=a b+a c(分配律)
3.利用空间向量的数量积解的三类问题:长度、夹角、位置关系.
作业布置
作业: P9-10 习题1.1 第4,7,8,9题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修 第一章
1.1.2 空间向量的数量积运算
人教A版(2019)
教学目标
学习目标 数学素养
1.理解空间向量的夹角的概念. 1.空间抽象素养.
2.掌握空间向量数量积的概念、性质、计算方法及运算规律. 2.空间抽象素养和数学运算素养.
3.会用两个向量数量积解决立体几何中的一些简单的问题. 3.逻辑推理素养和数学运算素养.
温故知新
1.平面向量的夹角
2.平面向量的垂直
已知两个非零向量是平面是上的任意一点,作,则叫做向量与 的夹角.记作
如果与的夹角是,我们就说与垂直,记作.
3.向量的投影向量
已知两个非零向量,它们的夹角为,我们把数量积叫做
向量与 的数量积(或内积),记作,即 .
规定:零向量与任一向量的数量积为0.
4.平面向量的数量积
如图,设是两个非零向量, 过的起点A和终点B,分别作所在直线的垂线,垂足分别为得到我们称上述变换为向量投影, 叫做向量上的投影向量.
新知探究
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以象平面向量那样来定义.
如图,已知两个非零向量a,b,在空间任取一点O、作=a,=b,则∠AOB叫做向量a,b的夹角,记作
如果
通常规定,
0≤
新知探究
已知两个非零向量a,b,则|a||b|cos
a·b=|a||b|cos
结果为数值
特别地,零向量与任意向量的数量积为0.
由向量的数量积定义,可以得到:
a⊥b a b=0;
a·a= |a||a|cos
证明垂直
求长度
a·a也记作a2.
知新探究
在平面向量的学习中,我们学习了向量的投影,类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
如图, 在空间,向量a向向量b投影,由于它们是自由向量,因此可以将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,
.
向量c称为向量a在向量b上的投影向量.
知新探究
类似地,如图,可以将向量a向直线l投影.
如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量 ,向量称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
知新探究
空间向量数量积的运算律
(λa) b=λ(a b),λ∈R
a b=b a(交换律)
a (b+c)=a b+a c(分配律)
注意:数量积不满足结合律.
即(a b) c≠a (b c)
知新探究
1.对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量a,b,c,由a b=a c能得到b=c吗 如果不能,请举出反例.
2.对于三个均不为0的数a,b,c,若ab=c,则(或).对于向量a,b,若a·b=k,能否写成(或 )的形式
3.对于三个均不为0的数a,b,c,有(ab)c=a(bc).对于向量a,b,c,(a b)c=a(b c)成立吗 也就是说,向量的数量积满足结合律吗
1.对于三个向量,由 =不能得到=c.例如:如图所示,在长方体ABCD-中,向量与向量都垂
直,因此=0,显然, 不相等.
事实上,由 =得- =,进而得
,即向量与c垂直,但不一定有另外,当=0时,有 ==0,此时也不一定有.
知新探究
2.由,不能写成或的形式,即向量没有除法运算.向量有加法、减法、数乘和数量积运算,没有实数除以向量和向量除以向量的运算.
3.对于向量,c,()c= (b不成立,也就是说,向量数量积运算不满足结合律.
例如:任意取三个不共面的向量,c,其中,c不共线,(b是一个数与向量做数乘运算,()c是一个数与向量做数乘运算,而向量,c不共线,所以()c与(b不相等.
数量积的运算只满足交换律,分配律及数乘结合律,但不满足乘法结合律,即(a b)c不一定等于a(b c).这是由于(a b)c表示一个与c共线的向量,而
a(b c)表示一个与a共线的向量,而c与a不一定共线.
新知探究
【例1】如图,在正方体ABCD-A1B1C1D1中,求向量的夹角的大小.
解:
方法1:∵,
∵△D1AC为等边三角形,
∴,即,
分析:求两个向量的夹角,可以把其中一个向量平移到与另一个向量的起点重合,从而转化为求平面角的大小;也可以用两个向量的数量积定义a·b=|a||b|cos
∴即为向量的夹角,
则向量的夹角为.
新知探究
【例1】如图,在正方体ABCD-A1B1C1D1中,求向量的夹角的大小.
解:
方法2:设正方体的棱长为1,则
又,,
=0+1+0+0=1
∴,
∵,
∴,
则向量的夹角为.
新知探究
两个非零向量夹角求法的两个途径:
1.转化求角:把向量夹角转化为平面几何中的对应角,利用解三角形的知识求解.
2.利用数量积求夹角:
⑴求向量数量积及向量的模;
⑵运用公式cos
⑶利用向量的夹角求分弦值,继而求角的大小.
注意:可以用非零向量夹角的求法,求异面直线所成的角.
①根据题设条件在所求的异面直线上取两个向量;
②异面直线所成角的问题转化为向量夹角问题.
初试身手
1.在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,AA1= ,求异面直线BA1与AC所成角的余弦值.
解:
∵,,
且0,AB=1
∴=-1
又,,
∴,
∵异面直线所成角的范围是(0,],
∴异面直线BA1与AC所成角的余弦值为.
新知探究
【例2】如图,在平行六面体ABCD-A'B'C'D中,AB=5,AD=3,AA'=7,∠BAD=60°,
∠BAA'=∠DAA'=45°.求:
⑴ ; ⑵AC'的长(精确到0.1).
解:
⑴
=7.5.
⑵
.
所以AC'≈13.3.
新知探究
利用空间向量求线段的长度或两点的距离:
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以向量的线性运算及数量积运算表示出来,因此立体几何中的许多问题可以用向量运算的方法加以解决.
⑴结合图形将所求线段用向量表示;
⑵用已知模和夹角的向量表示该向量;
⑶利用,通过计算求出,即得所求线段的长度或两点间的距离.
初试身手
2.如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又AB=4,AC=6,BD=8,求CD的长.
解:
∵CA AB,BD AB,
∴,
∵,且0,0,
∴
=68.
∴,即CD的长为.
新知探究
【例3】如图,m,n是平面α内的两条相交直线,直线l与α的交点为B,且l⊥m,l⊥n,求证:l⊥α.
分析:要证明l⊥α,就是要证明l垂直于α内的任意内的任意一条直线g(直线与平面垂直的定义).如果我们能在g和m,
n之间建立某种联系,并由l⊥m,l⊥n,得到l⊥g,那么就能解决此问题.
新知探究
【例3】如图,m,n是平面α内的两条相交直线,直线l与α的交点为B,且l⊥m,l⊥n,求证:l⊥α.
证明:
在平面α内作任意一条直线g,分别在直线l,m,n,g上取非零向量l,m,n,g.
由向量共面的充要条件可知,
存在唯一的有序买数对(x,y),使
将上式两边分别与向量l作数量积运算,得
因为l·m=0,l·n=0,所以l · g=0.
g=xm+yn.
所以l⊥g.
这就证明了直线l垂直于平面α内的任意一条直线,所以l⊥α.
因为直线m与n相交,所以向量m,n不平行.
l · g=xl·m+yl·n.
例3即为直线与平面垂直的判定定理的证明过程.尝试用综合几何证明这个定理,并比较两种方法,你能从中体会到向量方法的优越性吗?
初试身手
3.如图所示,在三棱锥中A-BCD,DA,DB,DC两两垂直,且DB=DC=DA=2,E为BC的中点.
⑴证明:AE⊥BC;
⑵求直线AE与DC所成角的余弦值.
⑴证明:∵DA,DB,DC两两垂直,
∴
=
==0.
又∵
,
∴,
则AE⊥BC.
初试身手
3.如图所示,在三棱锥中A-BCD,DA,DB,DC两两垂直,且DB=DC=DA=2,E为BC的中点.
⑴证明:AE⊥BC;
⑵求直线AE与DC所成角的余弦值.
⑵∵
解:
∴.
==2.
而.
=
则直线AE与DC所成角的余弦值为.
课堂小结
1.空间向量的夹角、数量积、投影向量
已知两个非零向量a,b,在空间任取一点O、作=a,=b,则∠AOB叫做向量a,b的夹角,记作
已知两个非零向量a,b,则|a||b|cos
.
如图,向量c称为向量a在向量b上的投影向量.
如图,可以将向量a向直线l投影.
如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量 ,向量称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
课堂小结
2.空间向量数量积的运算律
(λa) b=λ(a b),λ∈R
a b=b a(交换律)
a (b+c)=a b+a c(分配律)
3.利用空间向量的数量积解的三类问题:长度、夹角、位置关系.
作业布置
作业: P9-10 习题1.1 第4,7,8,9题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
