选择必修 第一章 1.3.1 空间间直角坐标系 课件(共24张PPT)
文档属性
| 名称 | 选择必修 第一章 1.3.1 空间间直角坐标系 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-18 10:34:49 | ||
图片预览








文档简介
(共24张PPT)
选择必修 第一章
1.3.1 空间直角坐标系
人教A版(2019)
教学目标
学习目标 数学素养
1.了解空间直角坐标系,并掌握空间直角坐标系的画法,感受建立空间直角坐标系的必要性. 1.数学类比素养和空间想象素养.
2.会在空间直角坐标系中写出所给定点、向量的坐标. 2.数学抽象素养和数学运算素养.
温故知新
1.空间向量基本定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z).使得
p=xa+yb+zc.
把三个不共面的向量{a,b,c}叫做空间的一个基底,
a,b,c都叫做基向量.
空间任意三个不共面的向量都可以构成空间的一个基底.
温故知新
2.平面向量的正交分解及坐标表示
如图,在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量作为基底.单位正交基底:.
∟
把一个向量分解为两个互相垂直的向量,叫作把向量作正交分解.
特殊情形:,称为单位正交基底 .
对平面内任一向量,由平面向量基本定理知,有且只有一对实数,使得
这样,平面内任一向量都可以由唯一确定,我们把有序数对叫做向量的坐标,记作
新知探究
学习了空间向量基本定理,建立了“空间基底”的概念,我们就可以利用基底表示任意一个空间向量,进而把空间向量的运算转化为基向量的运算. 所以,基底概念的引入为几何问题代数化奠定了基础.
在平面向量中,我们以平面直角坐标系中与x轴、y轴方向相同的两个单位向量i,j为基底,建立了向量的坐标与点的坐标的一一对应关系,从而把平面向量的运算化归为数的运算.
类似地,为了把空间向量的运算化归为数的运算,能否利用空间向量基本定理和空间的单位正交基底,建立空间直角坐标系,进而建立空间向量的坐标与空间点的坐标的一一对应呢?
平面向量
空间向量
新知探究
我们知道,平面直角坐标系由平面内两条互相垂直、原点重合的数轴组成.利用单位正交基底概念,我们还可以这样理解平面直角坐标系.
如图,在平面内选取一点O和一个单位正交基底{i,j},以O为原点,分别以i,j 的方向为正方向,以它们的长度为单位长度两条数轴:x轴、y轴,那么就建立了平面直角坐标系Oxy.
x
y
z
i
j
k
O
类似地,在空间选定一点O和一个单位正交基底{i,j,k }(如图).以点О为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz.
在空间直角坐标系中O叫做原点,i,j,k都叫做坐标向量,
通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.
新知探究
空间直角坐标系画法.
在空间中,在x、y轴的基础上添加与x、y轴都垂直的z轴.
借鉴斜二测画法,在画空间直角坐标系Oxy时,让x轴与y轴所成的角为135°(或45°),即∠xOy=135°(或45°),画z轴和y轴垂直,即∠yOz=90°.如图所示,
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
y
x
z
新知探究
在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?
z
如图,在空间直角坐标系Oxyz中,,,为坐标向量,对空间任意一点A,对应一个向量,且点A的位置由向量唯一确定,由空间向量基本定理,存在唯一的有序实数组(,,),使
=++.
在单位正交基底{i,j,k}下与向量对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z).其中x叫做横坐标,y叫做纵坐标,z叫做竖坐标.
横坐标
竖坐标
纵坐标
记作A(x, y, z).
知新探究
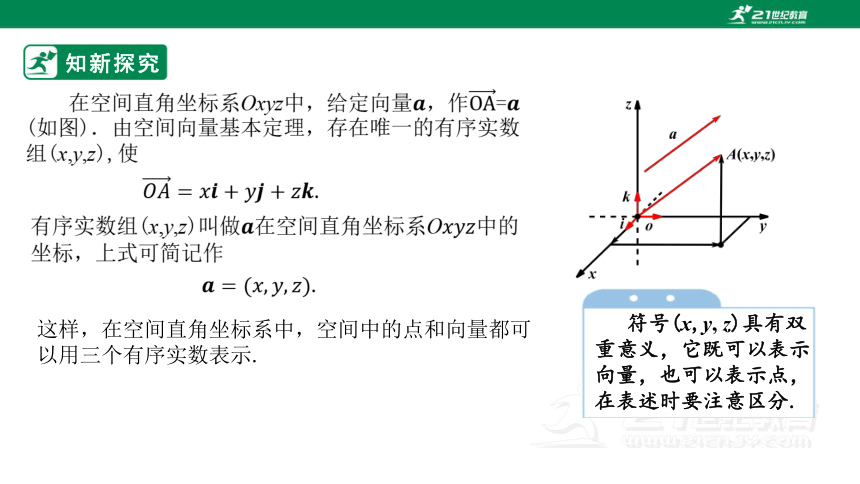
在空间直角坐标系Oxyz中,给定向量,作=
(如图).由空间向量基本定理,存在唯一的有序实数组(x,y,z),使
.
有序实数组(x,y,z)叫做在空间直角坐标系O中的坐标,上式可简记作
.
符号(x,y, z)具有双重意义,它既可以表示向量,也可以表示点,在表述时要注意区分.
这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
知新探究
在空间直角坐标系Oxyz中,对空间任意一点A,或任意一个向量,你能借助几何直观确定它们的坐标(x,y, z)吗?
事实上,如图,过点A分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点B,C和D.
可以证明在x轴、y轴、z轴上的投影向量分别为,,,且 =++.
E
你能给出证明吗?
,
.
设点B,C和D在x轴、y轴和z轴上的坐标分别是x,y和z,那么点A(向量)的坐标为(x,y,z).
这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
知新探究
确定空间中一个点A或任意一个向量a的坐标的方法:
点A的坐标
给定的向量 的坐标
的坐标
应用空间向量基本定理确定坐标
根据几何直观确定 在各坐标轴上的投影向量,从而求得坐标
新知探究
【例1】如图,在长方体OABC-D A B C 中,OA=3,OC=4,OD =2,以{, }为单位正交基底,建立如图所示的空间直角坐标系Oxyz.
⑴写出D ,C ,A ,B 四点的坐标;
⑵写出向量, , , 坐标.
解:
⑴因为点D'在z轴上,且OD'=2,所以.
所以点D'的坐标是(0,0,2).
同理点C的坐标是(0,4,0).
点A'在x轴、y轴、z轴上的射影分别为A,O,D',它们在坐标轴上的坐标分别为3,0,2,所以点A'的坐标是(3,0,2).
点B'在x轴、y轴、z轴上的射影分别为A,C,D,它们在坐标轴上的坐标分别为3,4,2,所以点B'的坐标是(3,4,2).
新知探究
【例1】如图,在长方体OABC-D A B C 中,OA=3,OC=4,OD =2,以{, }为单位正交基底,建立如图所示的空间直角坐标系Oxyz.
⑴写出D ,C ,A ,B 四点的坐标;
⑵写出向量, , , 坐标.
解:
⑵=0i+4j+0k=(0,4,0);
=0i+0j-2k=(0,0,-2);
=-3i+4j+0k=(-3,4,0);
=-3i+4j+2k=(-3,4,2).
知新探究
特殊位置的点的坐标
O
x
y
z
1
1
1
A
D
C
B
E
F
点P的位置 原点O x轴上A y轴上B z轴上C
坐标形式
点P的位置 xOy面内D yOz面内E zOx面内F
坐标形式
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
坐标轴上的点至少有两个坐标等于0;
坐标面上的点至少有一个坐标等于0.
初试身手
1.如图,在直三棱柱ABC A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点,以为单位正交基底,建立如图所示的空间直角坐标系C xyz.
⑴写出B,C1,B1,M,N五点的坐标;
解:
点B在y轴上,且CB=1,所以=0i+j+0k,
所以点B的坐标是(0,1,0).
同理,点C1的坐标为(0,0,2).
点B1在x轴、y轴、z轴上的射影分别为C,B,C1,它们在坐标轴上的坐标分别为0,1,2,所以点B1的坐标是(0,1,2).
同理,点M的坐标为(,2),点N的坐标为(1,0,1).
初试身手
1.如图,在直三棱柱ABC A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点,以为单位正交基底,建立如图所示的空间直角坐标系C xyz.
⑵写出向量,, 的坐标.
解:
=i-j+k=(1,-1,1),
1=i-j+2k=(1,-1,2).
=(-1,1,-2).
新知探究
【例2】在空间直角坐标系中给定点M(1,-2,3).
⑴求它分别关于xOy平面和xOz平面的对称点;
⑵关于z轴和原点的对称点的坐标.
解:
⑴M(1,-2,3)关于坐标平面xOy对称的点是(1,-2,-3),
M(1,-2,3)关于xOz面对称的点是(1,2,3).
⑵M(1,-2,3)关于z轴对称点的坐标是(-1,2,3),
M(1,-2,3)关于坐标原点对称点的坐标是(-1,2,-3).
新知探究
对称性
点P(x,y,z)
关于坐标平面xOy的对称点为______________;
关于坐标平面yOz的对称点为______________;
关于坐标平面xOz的对称点为______________;
关于x轴的对称点为______________;
关于y轴的对称点为______________;
关于z轴的对称点为______________.
P1(x,y,-z)
P2(-x,y,z)
P3(x,-y,z)
P4(x,-y,-z)
P5(-x,y,-z)
P6(-x,-y,z)
初试身手
2.在空间坐标系Oxyz中,点M(2,-3,-4)在坐标平面xOy,xOz,yOz内的投影的坐标分别为 , , ,关于原点的对称点为 ,关于x轴的对称点为 .
(2,-3,0)
(2,0,-4)
(0,-3,-4)
(-2,3,4)
(2,3,4)
课堂小结
1.空间直角坐标系
2.空间坐标系内点或向量的坐标表示
在空间选定一点O和一个单位正交基底{i,j,k }.以点О为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz.
x
y
z
i
j
k
O
在空间直角坐标系中O叫做原点,i,j,k都叫做坐标向量.
在空间直角坐标系Oxyz中,给定向量,作=,
.即.
在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
作业布置
作业: P18 练习 第3题 P22 习题1.3 第2,3题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修 第一章
1.3.1 空间直角坐标系
人教A版(2019)
教学目标
学习目标 数学素养
1.了解空间直角坐标系,并掌握空间直角坐标系的画法,感受建立空间直角坐标系的必要性. 1.数学类比素养和空间想象素养.
2.会在空间直角坐标系中写出所给定点、向量的坐标. 2.数学抽象素养和数学运算素养.
温故知新
1.空间向量基本定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z).使得
p=xa+yb+zc.
把三个不共面的向量{a,b,c}叫做空间的一个基底,
a,b,c都叫做基向量.
空间任意三个不共面的向量都可以构成空间的一个基底.
温故知新
2.平面向量的正交分解及坐标表示
如图,在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量作为基底.单位正交基底:.
∟
把一个向量分解为两个互相垂直的向量,叫作把向量作正交分解.
特殊情形:,称为单位正交基底 .
对平面内任一向量,由平面向量基本定理知,有且只有一对实数,使得
这样,平面内任一向量都可以由唯一确定,我们把有序数对叫做向量的坐标,记作
新知探究
学习了空间向量基本定理,建立了“空间基底”的概念,我们就可以利用基底表示任意一个空间向量,进而把空间向量的运算转化为基向量的运算. 所以,基底概念的引入为几何问题代数化奠定了基础.
在平面向量中,我们以平面直角坐标系中与x轴、y轴方向相同的两个单位向量i,j为基底,建立了向量的坐标与点的坐标的一一对应关系,从而把平面向量的运算化归为数的运算.
类似地,为了把空间向量的运算化归为数的运算,能否利用空间向量基本定理和空间的单位正交基底,建立空间直角坐标系,进而建立空间向量的坐标与空间点的坐标的一一对应呢?
平面向量
空间向量
新知探究
我们知道,平面直角坐标系由平面内两条互相垂直、原点重合的数轴组成.利用单位正交基底概念,我们还可以这样理解平面直角坐标系.
如图,在平面内选取一点O和一个单位正交基底{i,j},以O为原点,分别以i,j 的方向为正方向,以它们的长度为单位长度两条数轴:x轴、y轴,那么就建立了平面直角坐标系Oxy.
x
y
z
i
j
k
O
类似地,在空间选定一点O和一个单位正交基底{i,j,k }(如图).以点О为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz.
在空间直角坐标系中O叫做原点,i,j,k都叫做坐标向量,
通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.
新知探究
空间直角坐标系画法.
在空间中,在x、y轴的基础上添加与x、y轴都垂直的z轴.
借鉴斜二测画法,在画空间直角坐标系Oxy时,让x轴与y轴所成的角为135°(或45°),即∠xOy=135°(或45°),画z轴和y轴垂直,即∠yOz=90°.如图所示,
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
y
x
z
新知探究
在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?
z
如图,在空间直角坐标系Oxyz中,,,为坐标向量,对空间任意一点A,对应一个向量,且点A的位置由向量唯一确定,由空间向量基本定理,存在唯一的有序实数组(,,),使
=++.
在单位正交基底{i,j,k}下与向量对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z).其中x叫做横坐标,y叫做纵坐标,z叫做竖坐标.
横坐标
竖坐标
纵坐标
记作A(x, y, z).
知新探究
在空间直角坐标系Oxyz中,给定向量,作=
(如图).由空间向量基本定理,存在唯一的有序实数组(x,y,z),使
.
有序实数组(x,y,z)叫做在空间直角坐标系O中的坐标,上式可简记作
.
符号(x,y, z)具有双重意义,它既可以表示向量,也可以表示点,在表述时要注意区分.
这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
知新探究
在空间直角坐标系Oxyz中,对空间任意一点A,或任意一个向量,你能借助几何直观确定它们的坐标(x,y, z)吗?
事实上,如图,过点A分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点B,C和D.
可以证明在x轴、y轴、z轴上的投影向量分别为,,,且 =++.
E
你能给出证明吗?
,
.
设点B,C和D在x轴、y轴和z轴上的坐标分别是x,y和z,那么点A(向量)的坐标为(x,y,z).
这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
知新探究
确定空间中一个点A或任意一个向量a的坐标的方法:
点A的坐标
给定的向量 的坐标
的坐标
应用空间向量基本定理确定坐标
根据几何直观确定 在各坐标轴上的投影向量,从而求得坐标
新知探究
【例1】如图,在长方体OABC-D A B C 中,OA=3,OC=4,OD =2,以{, }为单位正交基底,建立如图所示的空间直角坐标系Oxyz.
⑴写出D ,C ,A ,B 四点的坐标;
⑵写出向量, , , 坐标.
解:
⑴因为点D'在z轴上,且OD'=2,所以.
所以点D'的坐标是(0,0,2).
同理点C的坐标是(0,4,0).
点A'在x轴、y轴、z轴上的射影分别为A,O,D',它们在坐标轴上的坐标分别为3,0,2,所以点A'的坐标是(3,0,2).
点B'在x轴、y轴、z轴上的射影分别为A,C,D,它们在坐标轴上的坐标分别为3,4,2,所以点B'的坐标是(3,4,2).
新知探究
【例1】如图,在长方体OABC-D A B C 中,OA=3,OC=4,OD =2,以{, }为单位正交基底,建立如图所示的空间直角坐标系Oxyz.
⑴写出D ,C ,A ,B 四点的坐标;
⑵写出向量, , , 坐标.
解:
⑵=0i+4j+0k=(0,4,0);
=0i+0j-2k=(0,0,-2);
=-3i+4j+0k=(-3,4,0);
=-3i+4j+2k=(-3,4,2).
知新探究
特殊位置的点的坐标
O
x
y
z
1
1
1
A
D
C
B
E
F
点P的位置 原点O x轴上A y轴上B z轴上C
坐标形式
点P的位置 xOy面内D yOz面内E zOx面内F
坐标形式
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
坐标轴上的点至少有两个坐标等于0;
坐标面上的点至少有一个坐标等于0.
初试身手
1.如图,在直三棱柱ABC A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点,以为单位正交基底,建立如图所示的空间直角坐标系C xyz.
⑴写出B,C1,B1,M,N五点的坐标;
解:
点B在y轴上,且CB=1,所以=0i+j+0k,
所以点B的坐标是(0,1,0).
同理,点C1的坐标为(0,0,2).
点B1在x轴、y轴、z轴上的射影分别为C,B,C1,它们在坐标轴上的坐标分别为0,1,2,所以点B1的坐标是(0,1,2).
同理,点M的坐标为(,2),点N的坐标为(1,0,1).
初试身手
1.如图,在直三棱柱ABC A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点,以为单位正交基底,建立如图所示的空间直角坐标系C xyz.
⑵写出向量,, 的坐标.
解:
=i-j+k=(1,-1,1),
1=i-j+2k=(1,-1,2).
=(-1,1,-2).
新知探究
【例2】在空间直角坐标系中给定点M(1,-2,3).
⑴求它分别关于xOy平面和xOz平面的对称点;
⑵关于z轴和原点的对称点的坐标.
解:
⑴M(1,-2,3)关于坐标平面xOy对称的点是(1,-2,-3),
M(1,-2,3)关于xOz面对称的点是(1,2,3).
⑵M(1,-2,3)关于z轴对称点的坐标是(-1,2,3),
M(1,-2,3)关于坐标原点对称点的坐标是(-1,2,-3).
新知探究
对称性
点P(x,y,z)
关于坐标平面xOy的对称点为______________;
关于坐标平面yOz的对称点为______________;
关于坐标平面xOz的对称点为______________;
关于x轴的对称点为______________;
关于y轴的对称点为______________;
关于z轴的对称点为______________.
P1(x,y,-z)
P2(-x,y,z)
P3(x,-y,z)
P4(x,-y,-z)
P5(-x,y,-z)
P6(-x,-y,z)
初试身手
2.在空间坐标系Oxyz中,点M(2,-3,-4)在坐标平面xOy,xOz,yOz内的投影的坐标分别为 , , ,关于原点的对称点为 ,关于x轴的对称点为 .
(2,-3,0)
(2,0,-4)
(0,-3,-4)
(-2,3,4)
(2,3,4)
课堂小结
1.空间直角坐标系
2.空间坐标系内点或向量的坐标表示
在空间选定一点O和一个单位正交基底{i,j,k }.以点О为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz.
x
y
z
i
j
k
O
在空间直角坐标系中O叫做原点,i,j,k都叫做坐标向量.
在空间直角坐标系Oxyz中,给定向量,作=,
.即.
在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
作业布置
作业: P18 练习 第3题 P22 习题1.3 第2,3题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
