人教版2023-2024学年度下学期七年级期末模拟预测数学卷(含答案)
文档属性
| 名称 | 人教版2023-2024学年度下学期七年级期末模拟预测数学卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 579.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 14:50:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟预测卷2023-2024学年数学七年级下册人教版
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,数轴上点A表示的数可能是( )
A. B. C. D.
2.如图,在中,是角平分线,,,的度数为( )
A. B. C. D.
3.把变形成用x表示y的形式为( )
A. B. C. D.
4.若关于、的二元一次方程组的解满足,则的取值范围是( )
A. B. C. D.
5.如图,要在一条主路旁建一座自来水中转站,向点处的小区引自来水,在什么地方建造,才能使输水管道最短?并说明理由.下列说法正确的是( )
A.点,两点之间线段最短 B.点,垂线段最短
C.点,两点确定一条直线 D.点,垂线段最短
6.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为 ,棋子“炮”的点的坐标为 ,则表示棋子“馬”的点的坐标为( )
A. B. C. D.
7.某校团员代表在“学雷锋”活动中购买点心与水果去敬老院慰问15名孤寡老人,其中要求给每位老人50元的慰问金,此次活动经费不超过990元,问最多可以给每位老人准备用于买点心与水果的费用为( )
A.20元 B.18元 C.17元 D.16元
8.绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中AB、CD都与地面平行,AM与BC平行,若,则的度数为( )
A. B. C. D.
9.某校七年级学生到校方式情况的统计图如图所示.若骑自行车到校的学生有100人,则乘公共汽车到校的学生有( )
A.60人 B.80人 C.160人 D.400人
10.在平面直角坐标系中,对于点,我们把叫做点P的伴随点,已知的伴随点为,点的伴随点为,点的伴随点为,这样依次得到,若点的坐标为,则点的坐标为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分.
11.“x与6的和小于17”用不等式表示为 .
12.已知x,y为二元一次方程组 的解, 则 .
13.如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.若∠ABE=150°,∠CDF=160°,则∠EPF的度数是 .
14.在平面直角坐标系中,若有两点,,利用平移知识可得到线段AB中点的坐标为.
请利用以上结论解决问题:若点,,线段EF的中点M恰好位于y轴上,且到x轴的距离是3,则点E的坐标为 .
15.商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.现有27元钱,最多可以购买该商品的件数是 .
16.已知一个样本有40个数据,把它分成5组,第一组到第四组的频数分别是10、4、、,第五组的频率是0.1,则的值为 .
三、解答题:本题共8小题,共72分,解答应写出文字说明、证明过程或演算步骤.
17.计算:.
18.解方程组:
19. 解不等式:并求它的所有整数解的和.
20.已知:EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB.
21.某校准备组织七年级400名学生参加夏令营,已知满员时,用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)若学校计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
①请你设计出所有的租车方案;
②若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的租车方案,并求出最少租金.
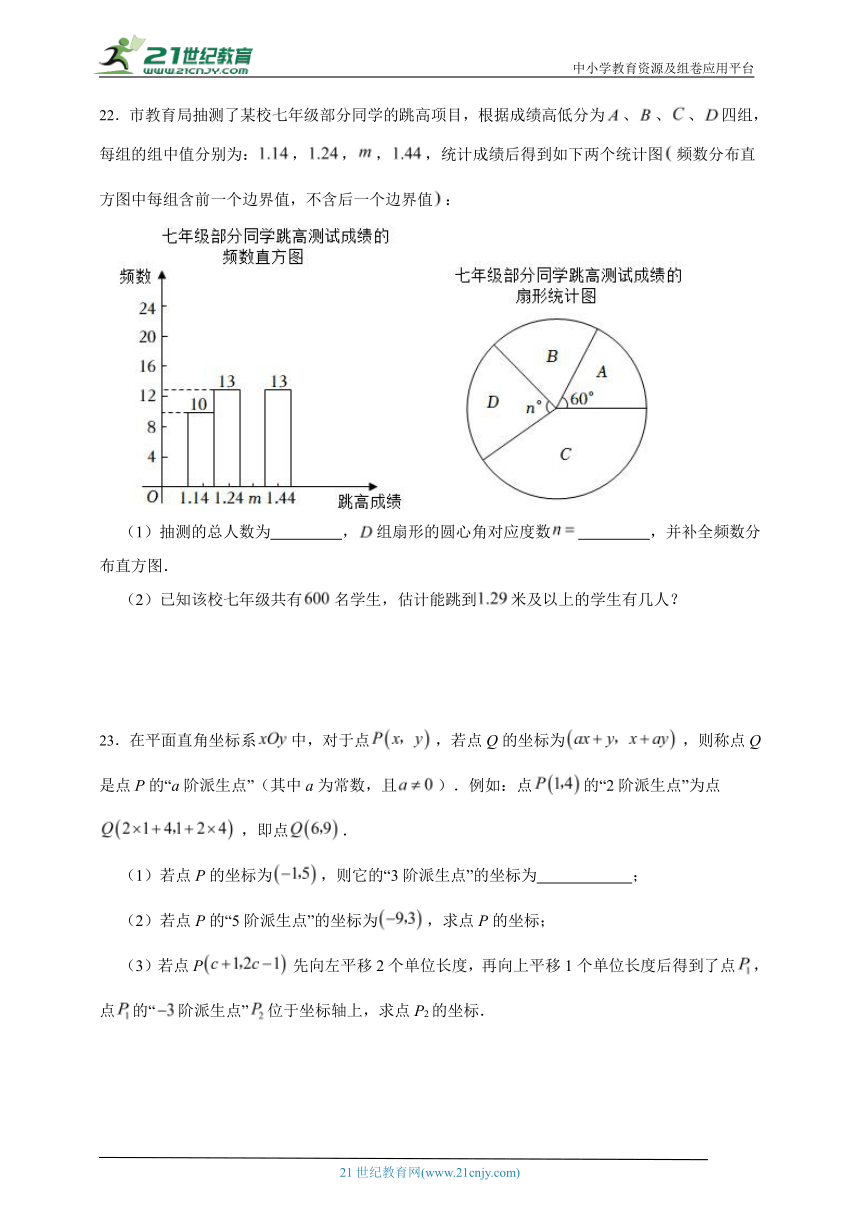
22.市教育局抽测了某校七年级部分同学的跳高项目,根据成绩高低分为、、、四组,每组的组中值分别为:,,,,统计成绩后得到如下两个统计图频数分布直方图中每组含前一个边界值,不含后一个边界值:
(1)抽测的总人数为 ,组扇形的圆心角对应度数 ,并补全频数分布直方图.
(2)已知该校七年级共有名学生,估计能跳到米及以上的学生有几人?
23.在平面直角坐标系中,对于点,若点Q的坐标为,则称点Q是点P的“a阶派生点”(其中a为常数,且).例如:点的“2阶派生点”为点,即点.
(1)若点P的坐标为,则它的“3阶派生点”的坐标为 ;
(2)若点P的“5阶派生点”的坐标为,求点P的坐标;
(3)若点P先向左平移2个单位长度,再向上平移1个单位长度后得到了点,点的“阶派生点”位于坐标轴上,求点P2的坐标.
24.我们定义:使方程(组)与不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“梦想解”.
例:已知方程与不等式,方程的解为,使得不等式也成立,则称“”为方程和不等式的“梦想解”
(1)已知①,②,③,试判断方程解是否为它与它们中某个不等式的“梦想解”;
(2)若关于x,y的二元一次方程组的解是不等式组的梦想解,且m为整数,求m的值.
(3)若关于x的方程的解是关于x的不等式组的“梦想解”,且此时不等式组有7个整数解,试求m的取值范围.
答案
1.C
2.C
3.A
4.A
5.B
6.D
7.D
8.D
9.C
10.C
11.
12.1
13.50°
14.或
15.10件
16.6
17.解:
18.解法1:由①,得:③
把③代入②,得
解得:.
把代入③,解得:.
所以,方程组的解是.
解法2:①×2,得:③
③-②,得:.
把代入③,解得:.
所以,方程组的解是.
19.解:,
解①得:,
解②得:.
则不等式组的解集是:.
∴它的所有整数解为:,0,1,
∴它的所有整数解的和.
20.证明:∵EF⊥AB,CD⊥AB,
∴,
∴∠EFB=∠DCF,
∵∠EFB=∠GDC,
∴∠DCF=∠GDC,
∴,
∴∠AGD=∠ACB.
21.(1)1辆小客车和1辆大客车都坐满后一次可送65名学生;(2)①方案一:小客车20车、大客车0辆;方案二:小客车11辆,大客车4辆;方案三:小客车2辆,大客车8辆;②方案三租金最少,最少租金为3440元.
22.(1)60;78
(2)解:人.
答:能跳到米及以上的学生有人.
23.(1)
(2)解:由题意,得:,
解得:,
∴点P的坐标为;
(3)解:∵点先向左平移2个单位长度,再向上平移1个单位长度后得到了点
∴点
∴的“阶派生点”为:
即
当点在x轴上
,
解得:;
此时;
当点在y轴上
,
解得:;
此时;
∴点的坐标或.
24.(1)解:解方程得,
解①得:,故方程不是①的“梦想解”;
解②得:,故方程不是②“梦想解”;
解③得:,故方程是③的“梦想解”;
故答案为:③
(2)解:解方程
得:
∴
∵解是不等式组的梦想解
∴
∴
m为整数,
∴m为14或15;
(3)解:解不等式组得:,
不等式组的整数解有7个,
令整数的值为,,,,,,
则有:,.
故,
且,
,
,
,
,
解方程得:,
方程是关于的不等式组的“梦想解”,
,
解得,
综上的取值范围是.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟预测卷2023-2024学年数学七年级下册人教版
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,数轴上点A表示的数可能是( )
A. B. C. D.
2.如图,在中,是角平分线,,,的度数为( )
A. B. C. D.
3.把变形成用x表示y的形式为( )
A. B. C. D.
4.若关于、的二元一次方程组的解满足,则的取值范围是( )
A. B. C. D.
5.如图,要在一条主路旁建一座自来水中转站,向点处的小区引自来水,在什么地方建造,才能使输水管道最短?并说明理由.下列说法正确的是( )
A.点,两点之间线段最短 B.点,垂线段最短
C.点,两点确定一条直线 D.点,垂线段最短
6.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为 ,棋子“炮”的点的坐标为 ,则表示棋子“馬”的点的坐标为( )
A. B. C. D.
7.某校团员代表在“学雷锋”活动中购买点心与水果去敬老院慰问15名孤寡老人,其中要求给每位老人50元的慰问金,此次活动经费不超过990元,问最多可以给每位老人准备用于买点心与水果的费用为( )
A.20元 B.18元 C.17元 D.16元
8.绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中AB、CD都与地面平行,AM与BC平行,若,则的度数为( )
A. B. C. D.
9.某校七年级学生到校方式情况的统计图如图所示.若骑自行车到校的学生有100人,则乘公共汽车到校的学生有( )
A.60人 B.80人 C.160人 D.400人
10.在平面直角坐标系中,对于点,我们把叫做点P的伴随点,已知的伴随点为,点的伴随点为,点的伴随点为,这样依次得到,若点的坐标为,则点的坐标为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分.
11.“x与6的和小于17”用不等式表示为 .
12.已知x,y为二元一次方程组 的解, 则 .
13.如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.若∠ABE=150°,∠CDF=160°,则∠EPF的度数是 .
14.在平面直角坐标系中,若有两点,,利用平移知识可得到线段AB中点的坐标为.
请利用以上结论解决问题:若点,,线段EF的中点M恰好位于y轴上,且到x轴的距离是3,则点E的坐标为 .
15.商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.现有27元钱,最多可以购买该商品的件数是 .
16.已知一个样本有40个数据,把它分成5组,第一组到第四组的频数分别是10、4、、,第五组的频率是0.1,则的值为 .
三、解答题:本题共8小题,共72分,解答应写出文字说明、证明过程或演算步骤.
17.计算:.
18.解方程组:
19. 解不等式:并求它的所有整数解的和.
20.已知:EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB.
21.某校准备组织七年级400名学生参加夏令营,已知满员时,用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)若学校计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
①请你设计出所有的租车方案;
②若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的租车方案,并求出最少租金.
22.市教育局抽测了某校七年级部分同学的跳高项目,根据成绩高低分为、、、四组,每组的组中值分别为:,,,,统计成绩后得到如下两个统计图频数分布直方图中每组含前一个边界值,不含后一个边界值:
(1)抽测的总人数为 ,组扇形的圆心角对应度数 ,并补全频数分布直方图.
(2)已知该校七年级共有名学生,估计能跳到米及以上的学生有几人?
23.在平面直角坐标系中,对于点,若点Q的坐标为,则称点Q是点P的“a阶派生点”(其中a为常数,且).例如:点的“2阶派生点”为点,即点.
(1)若点P的坐标为,则它的“3阶派生点”的坐标为 ;
(2)若点P的“5阶派生点”的坐标为,求点P的坐标;
(3)若点P先向左平移2个单位长度,再向上平移1个单位长度后得到了点,点的“阶派生点”位于坐标轴上,求点P2的坐标.
24.我们定义:使方程(组)与不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“梦想解”.
例:已知方程与不等式,方程的解为,使得不等式也成立,则称“”为方程和不等式的“梦想解”
(1)已知①,②,③,试判断方程解是否为它与它们中某个不等式的“梦想解”;
(2)若关于x,y的二元一次方程组的解是不等式组的梦想解,且m为整数,求m的值.
(3)若关于x的方程的解是关于x的不等式组的“梦想解”,且此时不等式组有7个整数解,试求m的取值范围.
答案
1.C
2.C
3.A
4.A
5.B
6.D
7.D
8.D
9.C
10.C
11.
12.1
13.50°
14.或
15.10件
16.6
17.解:
18.解法1:由①,得:③
把③代入②,得
解得:.
把代入③,解得:.
所以,方程组的解是.
解法2:①×2,得:③
③-②,得:.
把代入③,解得:.
所以,方程组的解是.
19.解:,
解①得:,
解②得:.
则不等式组的解集是:.
∴它的所有整数解为:,0,1,
∴它的所有整数解的和.
20.证明:∵EF⊥AB,CD⊥AB,
∴,
∴∠EFB=∠DCF,
∵∠EFB=∠GDC,
∴∠DCF=∠GDC,
∴,
∴∠AGD=∠ACB.
21.(1)1辆小客车和1辆大客车都坐满后一次可送65名学生;(2)①方案一:小客车20车、大客车0辆;方案二:小客车11辆,大客车4辆;方案三:小客车2辆,大客车8辆;②方案三租金最少,最少租金为3440元.
22.(1)60;78
(2)解:人.
答:能跳到米及以上的学生有人.
23.(1)
(2)解:由题意,得:,
解得:,
∴点P的坐标为;
(3)解:∵点先向左平移2个单位长度,再向上平移1个单位长度后得到了点
∴点
∴的“阶派生点”为:
即
当点在x轴上
,
解得:;
此时;
当点在y轴上
,
解得:;
此时;
∴点的坐标或.
24.(1)解:解方程得,
解①得:,故方程不是①的“梦想解”;
解②得:,故方程不是②“梦想解”;
解③得:,故方程是③的“梦想解”;
故答案为:③
(2)解:解方程
得:
∴
∵解是不等式组的梦想解
∴
∴
m为整数,
∴m为14或15;
(3)解:解不等式组得:,
不等式组的整数解有7个,
令整数的值为,,,,,,
则有:,.
故,
且,
,
,
,
,
解方程得:,
方程是关于的不等式组的“梦想解”,
,
解得,
综上的取值范围是.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
