期末模拟卷(含答案)-2023-2024学年高中数学人教A版2019选择性必修第三册
文档属性
| 名称 | 期末模拟卷(含答案)-2023-2024学年高中数学人教A版2019选择性必修第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 532.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 10:28:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟卷-2023-2024学年高中数学人教A版2019选择性必修第三册
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.的展开式的常数项为( )
A.210 B.252 C. D.
2.已知,则( )。
A.5 B.2 C.5或2 D.2或6
3.篮球运动员在比赛中每次罚球得分的规则是:命中得1分,不命中得0分.已知某篮球运动员罚球命中的概率为0.8,设其罚球一次的得分为X,则( )
A., B.,
C., D.,
4.用红、黄、蓝三种不同颜色给如图所示的4块区域A、B、C、D涂色,要求同一区域用同一种颜色,有共公边的区域使用不同颜色,则共有涂色方法( )
A.14种 B.16种 C.20种 D.18种
5.袋子中有n个大小质地完全相同的球,其中4个为红球,其余均为黄球,从中不放回地依次随机摸出2个球,已知摸出的2个球都是红球的概率为,则两次摸到的球颜色不相同的概率为( )
A. B. C. D.
6.下列说法正确的是( )
A.线性回归分析中决定系数用来刻画回归的效果,若值越小,则模型的拟合效果越好
B.残差平方和越小的模型,拟合的效果越好
C.正态分布的图象越瘦高,越大
D.两个随机变量的线性相关性越强,则相关系数r的值越接近于1
7.学校决定于月日月日举行为期天的“数学节”活动,现安排,,,,五位同学担任本次活动的志愿者已知五位志愿者要全部安排且每天只安排位志愿者,要求月日、月日做志愿者的同学每人安排一天,月日到月日做志愿者的同学每人安排两天,则不同的安排方法一共有( )
A.种 B.种 C.种 D.种
8.如图,由观测数据的散点图可知,与的关系可以用模型拟合,设,利用最小二乘法求得关于的回归方程.已知,
,则( )
A. B. C.1 D..
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.设,则下列说法正确的是( )
A. B.
C. D.
10. 为了解推动出口后的亩收入情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值,样本方差,已知该种植区以往的亩收入服从正态分布,假设推动出口后的亩收入服从正态分布,则( )(参考:若随机变量Z服从正态分布,)
A. B.
C. D.
11.下列命题中正确的是( )
A.设随机变量X~N(0,1),若P(X>1)=p,则
B.一个袋子中有大小相同的3个红球、2个白球,从中一次随机摸出3个球,记摸出红球的个数为X,则
C.已知随机变量X~B(n,p),若E(X)=30,D(X)=20,则
D.若随机变量X~B(10,0.9),则当X=9时概率最大
三、填空题:本题共3小题,每小题5分,共15分.
12.已知的展开式中第5项与第8项的二项式系数相等,则 .
13.已知随机变量服从正态分布,且,则 .
14.泊松分布的概率分布列为,其中e为自然对数的底数,是泊松分布的均值.若随机变量X服从二项分布,当n很大且p很小时,二项分布近似于泊松分布,其中,即.现已知某种元件的次品率为0.01,抽检100个该种元件,则次品率小于的概率约为 .
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.已知二项式的展开式中,所有项的二项式系数之和为,各项的系数之和为,.
(1)求的值:
(2)求展开式中的系数.
16.某学校开展社会实践进社区活动,高二某班有六名男生和四名女生报名参加活动,从中随机一次性抽取5人参加社区活动,其余5人参加社区活动.
(1)求参加社区活动的同学中包含且不包含的概率;
(2)用表示参加社区活动的女生人数,求的分布列和数学期望.
17.从6名男生和5名女生中选出4人去参加某活动的志愿者.
(1)若4人中必须既有男生又有女生,则有多少种选法?
(2)先选出4人,再将这4人分配到两个不同的活动场地(每个场地均要有人去,1人只能去一个场地),则有多少种安排方法?
(3)若男 女生各需要2人,4人选出后安排与2名组织者合影留念(站一排),2名女生要求相邻,则有多少种不同的合影方法?
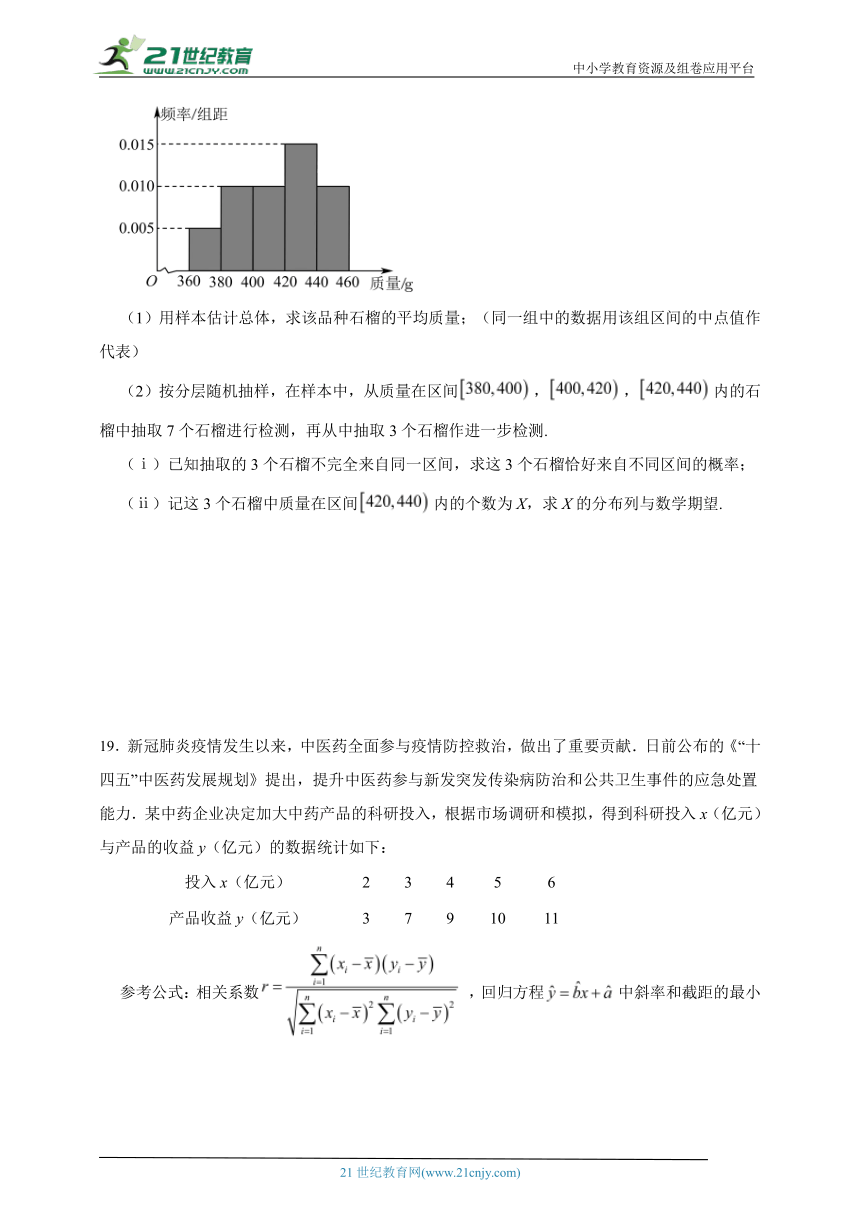
18.已知某种业公司培育了新品种的软籽石榴,从收获的果实中随机抽取了50个软籽石榴,按质量(单位:g)将它们分成5组:,,,,得到如下频率分布直方图.
(1)用样本估计总体,求该品种石榴的平均质量;(同一组中的数据用该组区间的中点值作代表)
(2)按分层随机抽样,在样本中,从质量在区间,,内的石榴中抽取7个石榴进行检测,再从中抽取3个石榴作进一步检测.
(ⅰ)已知抽取的3个石榴不完全来自同一区间,求这3个石榴恰好来自不同区间的概率;
(ⅱ)记这3个石榴中质量在区间内的个数为X,求X的分布列与数学期望.
19.新冠肺炎疫情发生以来,中医药全面参与疫情防控救治,做出了重要贡献.日前公布的《“十四五”中医药发展规划》提出,提升中医药参与新发突发传染病防治和公共卫生事件的应急处置能力.某中药企业决定加大中药产品的科研投入,根据市场调研和模拟,得到科研投入x(亿元)与产品的收益y(亿元)的数据统计如下:
投入x(亿元) 2 3 4 5 6
产品收益y(亿元) 3 7 9 10 11
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为:.
本题相关数据:.
(1)是否可用线性回归模型拟合y与x的关系?请用相关系数r加以说明(当时,变量x,y有较强的线性相关关系);
(2)利用最小二乘法求出y关于x的线性回归方程,并预测当科研投入为10亿元时产品的收益.
答案解析部分
1.C
2.C
3.D
4.D
5.C
6.B
7.C
8.C
9.B,D
10.B,C
11.A,B,D
12.11
13.0.2
14.
15.(1)因为,,
所以,解得;
(2)由通项公式,
令,可得,
所以展开式中的系数为.
16.(1)解:表示社区活动的同学中包含且不包含,
(2)解:随机变量的可能取值为:0,1,2,3,4,
用表格表示的分布列,如下表所示:
0 1 2 3 4
17.(1)从这11人中任选4人的选法有种,
其中只有男生的选法有种,
只有女生的选法有种,
故4人中必须既有男生又有女生的选法有种.
(2)从这11人中任选4人的选法有种,
若人数按1,3分配,则安排方法有种,
若人数按2,2分配,则安排方法有种,
所以共有种安排方法.
(3)因为男 女生各需要2人,所以选出4人的方法有种.
先排2名男生与2名组织者,有种排法,
再将2名女生“捆绑”在一起,放入5个空档中,有种方法,
所以共有种不同的合影方法.
18.(1)该品种石榴的平均质量为,
所以该品种石榴的平均质量为.
(2)由题可知,这7个石榴中,质量在,,上的频率比为,
所以抽取质量在,,上的石榴个数分别为2,2,3.
(ⅰ)记“抽取的3个石榴不完全来自同一区间”,“这3个石榴恰好来自不同区间”,
则,,
所以,
即这3个石榴恰好来自不同区间的概率为.
(ⅱ)由题意X的所有可能取值为0,1,2,3,
则,,
,,
所以X的分布列为
X 0 1 2 3
P
所以.
19.(1)解:由表中数据可得,,
,,,
,
变量x、y有较强的线性相关关系,可用线性回归模型拟合y与x的关系.
(2)解:由(1)知,所以,
故y关于x的回归方程为,
将代入回归方程可得,,
故预测投入10(亿元)时产品的收益为19.4(亿元).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟卷-2023-2024学年高中数学人教A版2019选择性必修第三册
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.的展开式的常数项为( )
A.210 B.252 C. D.
2.已知,则( )。
A.5 B.2 C.5或2 D.2或6
3.篮球运动员在比赛中每次罚球得分的规则是:命中得1分,不命中得0分.已知某篮球运动员罚球命中的概率为0.8,设其罚球一次的得分为X,则( )
A., B.,
C., D.,
4.用红、黄、蓝三种不同颜色给如图所示的4块区域A、B、C、D涂色,要求同一区域用同一种颜色,有共公边的区域使用不同颜色,则共有涂色方法( )
A.14种 B.16种 C.20种 D.18种
5.袋子中有n个大小质地完全相同的球,其中4个为红球,其余均为黄球,从中不放回地依次随机摸出2个球,已知摸出的2个球都是红球的概率为,则两次摸到的球颜色不相同的概率为( )
A. B. C. D.
6.下列说法正确的是( )
A.线性回归分析中决定系数用来刻画回归的效果,若值越小,则模型的拟合效果越好
B.残差平方和越小的模型,拟合的效果越好
C.正态分布的图象越瘦高,越大
D.两个随机变量的线性相关性越强,则相关系数r的值越接近于1
7.学校决定于月日月日举行为期天的“数学节”活动,现安排,,,,五位同学担任本次活动的志愿者已知五位志愿者要全部安排且每天只安排位志愿者,要求月日、月日做志愿者的同学每人安排一天,月日到月日做志愿者的同学每人安排两天,则不同的安排方法一共有( )
A.种 B.种 C.种 D.种
8.如图,由观测数据的散点图可知,与的关系可以用模型拟合,设,利用最小二乘法求得关于的回归方程.已知,
,则( )
A. B. C.1 D..
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.设,则下列说法正确的是( )
A. B.
C. D.
10. 为了解推动出口后的亩收入情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值,样本方差,已知该种植区以往的亩收入服从正态分布,假设推动出口后的亩收入服从正态分布,则( )(参考:若随机变量Z服从正态分布,)
A. B.
C. D.
11.下列命题中正确的是( )
A.设随机变量X~N(0,1),若P(X>1)=p,则
B.一个袋子中有大小相同的3个红球、2个白球,从中一次随机摸出3个球,记摸出红球的个数为X,则
C.已知随机变量X~B(n,p),若E(X)=30,D(X)=20,则
D.若随机变量X~B(10,0.9),则当X=9时概率最大
三、填空题:本题共3小题,每小题5分,共15分.
12.已知的展开式中第5项与第8项的二项式系数相等,则 .
13.已知随机变量服从正态分布,且,则 .
14.泊松分布的概率分布列为,其中e为自然对数的底数,是泊松分布的均值.若随机变量X服从二项分布,当n很大且p很小时,二项分布近似于泊松分布,其中,即.现已知某种元件的次品率为0.01,抽检100个该种元件,则次品率小于的概率约为 .
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.已知二项式的展开式中,所有项的二项式系数之和为,各项的系数之和为,.
(1)求的值:
(2)求展开式中的系数.
16.某学校开展社会实践进社区活动,高二某班有六名男生和四名女生报名参加活动,从中随机一次性抽取5人参加社区活动,其余5人参加社区活动.
(1)求参加社区活动的同学中包含且不包含的概率;
(2)用表示参加社区活动的女生人数,求的分布列和数学期望.
17.从6名男生和5名女生中选出4人去参加某活动的志愿者.
(1)若4人中必须既有男生又有女生,则有多少种选法?
(2)先选出4人,再将这4人分配到两个不同的活动场地(每个场地均要有人去,1人只能去一个场地),则有多少种安排方法?
(3)若男 女生各需要2人,4人选出后安排与2名组织者合影留念(站一排),2名女生要求相邻,则有多少种不同的合影方法?
18.已知某种业公司培育了新品种的软籽石榴,从收获的果实中随机抽取了50个软籽石榴,按质量(单位:g)将它们分成5组:,,,,得到如下频率分布直方图.
(1)用样本估计总体,求该品种石榴的平均质量;(同一组中的数据用该组区间的中点值作代表)
(2)按分层随机抽样,在样本中,从质量在区间,,内的石榴中抽取7个石榴进行检测,再从中抽取3个石榴作进一步检测.
(ⅰ)已知抽取的3个石榴不完全来自同一区间,求这3个石榴恰好来自不同区间的概率;
(ⅱ)记这3个石榴中质量在区间内的个数为X,求X的分布列与数学期望.
19.新冠肺炎疫情发生以来,中医药全面参与疫情防控救治,做出了重要贡献.日前公布的《“十四五”中医药发展规划》提出,提升中医药参与新发突发传染病防治和公共卫生事件的应急处置能力.某中药企业决定加大中药产品的科研投入,根据市场调研和模拟,得到科研投入x(亿元)与产品的收益y(亿元)的数据统计如下:
投入x(亿元) 2 3 4 5 6
产品收益y(亿元) 3 7 9 10 11
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为:.
本题相关数据:.
(1)是否可用线性回归模型拟合y与x的关系?请用相关系数r加以说明(当时,变量x,y有较强的线性相关关系);
(2)利用最小二乘法求出y关于x的线性回归方程,并预测当科研投入为10亿元时产品的收益.
答案解析部分
1.C
2.C
3.D
4.D
5.C
6.B
7.C
8.C
9.B,D
10.B,C
11.A,B,D
12.11
13.0.2
14.
15.(1)因为,,
所以,解得;
(2)由通项公式,
令,可得,
所以展开式中的系数为.
16.(1)解:表示社区活动的同学中包含且不包含,
(2)解:随机变量的可能取值为:0,1,2,3,4,
用表格表示的分布列,如下表所示:
0 1 2 3 4
17.(1)从这11人中任选4人的选法有种,
其中只有男生的选法有种,
只有女生的选法有种,
故4人中必须既有男生又有女生的选法有种.
(2)从这11人中任选4人的选法有种,
若人数按1,3分配,则安排方法有种,
若人数按2,2分配,则安排方法有种,
所以共有种安排方法.
(3)因为男 女生各需要2人,所以选出4人的方法有种.
先排2名男生与2名组织者,有种排法,
再将2名女生“捆绑”在一起,放入5个空档中,有种方法,
所以共有种不同的合影方法.
18.(1)该品种石榴的平均质量为,
所以该品种石榴的平均质量为.
(2)由题可知,这7个石榴中,质量在,,上的频率比为,
所以抽取质量在,,上的石榴个数分别为2,2,3.
(ⅰ)记“抽取的3个石榴不完全来自同一区间”,“这3个石榴恰好来自不同区间”,
则,,
所以,
即这3个石榴恰好来自不同区间的概率为.
(ⅱ)由题意X的所有可能取值为0,1,2,3,
则,,
,,
所以X的分布列为
X 0 1 2 3
P
所以.
19.(1)解:由表中数据可得,,
,,,
,
变量x、y有较强的线性相关关系,可用线性回归模型拟合y与x的关系.
(2)解:由(1)知,所以,
故y关于x的回归方程为,
将代入回归方程可得,,
故预测投入10(亿元)时产品的收益为19.4(亿元).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
