《立体图形的体积》整理与复习(课件)-2023-2024学年六年级上册数学人教版
文档属性
| 名称 | 《立体图形的体积》整理与复习(课件)-2023-2024学年六年级上册数学人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 14:10:52 | ||
图片预览



文档简介
(共39张PPT)
立体图形的体积
——整理与复习
义务教育人教版六年级下册
知识梳理
回忆一下,小学阶段我们学过的立体图形有哪些?
你能说一说吗?
复习导入
立体图形 表面积 计算公式
S=2(ab+ah+bh)
S=a×a× 6 = 6a2
S=2πrh+2πr2
复习回顾:
1、立体图形的表面积和体积有什么区别呢?
2、什么是表面积? 什么是体积?
知识梳理
同桌讨论,总结汇报。
知识梳理
一个立体图形所有面的面积总和,叫做它的表面积。
一个立体图形所占空间的大小,叫做它的体积。
复习回顾:
1、立体图形的表面积和体积有什么区别呢?
2、什么是表面积? 什么是体积?
1
2
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
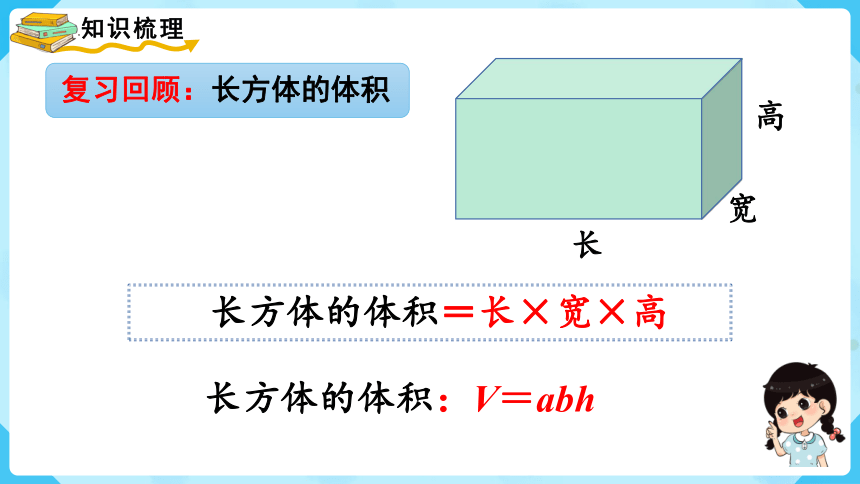
复习回顾:长方体的体积
知识梳理
长方体的体积=长×宽×高
长
高
宽
长方体的体积:V=abh
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
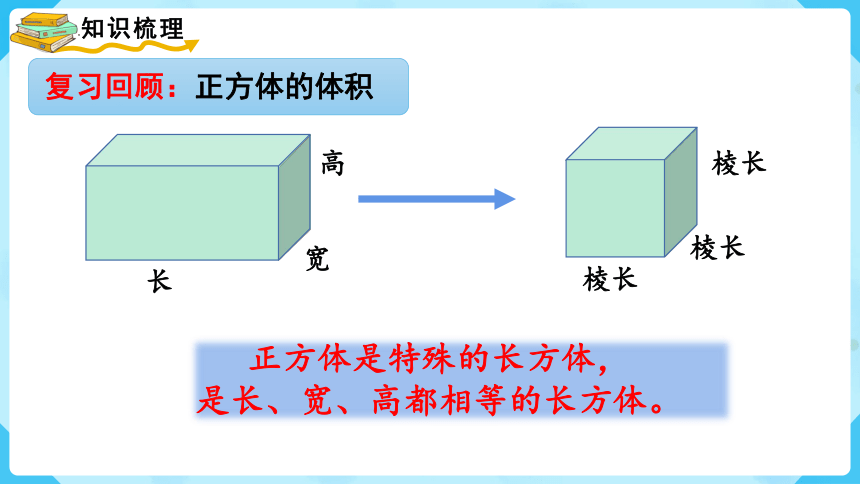
复习回顾:正方体的体积
知识梳理
棱长
棱长
棱长
长
高
宽
正方体是特殊的长方体,
是长、宽、高都相等的长方体。
复习回顾:正方体的体积
知识梳理
正方体的体积=棱长×棱长×棱长
棱长
棱长
棱长
长
高
宽
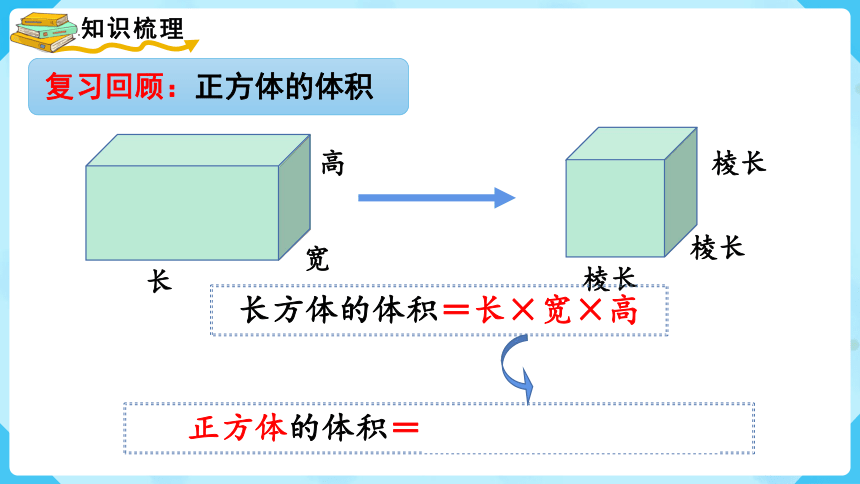
长方体的体积=长×宽×高
复习回顾:正方体的体积
知识梳理
正方体的体积=棱长×棱长×棱长
棱长
棱长
棱长
长
高
宽
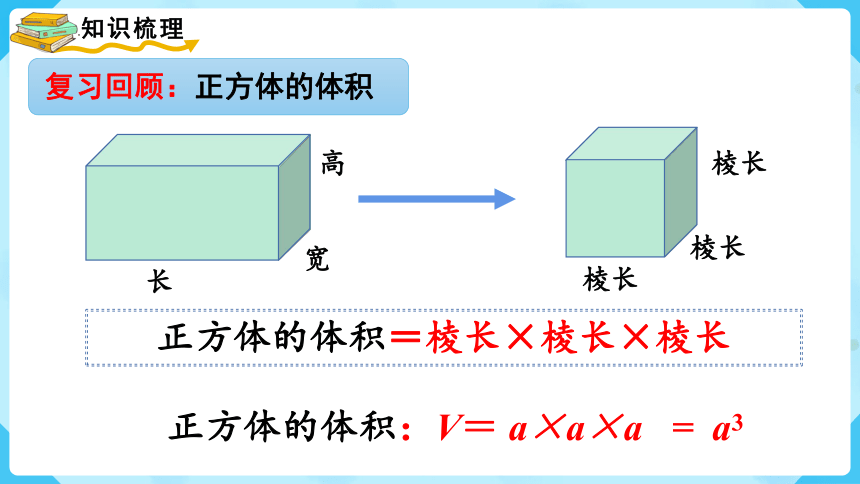
正方体的体积:V= a×a×a = a3
知识梳理
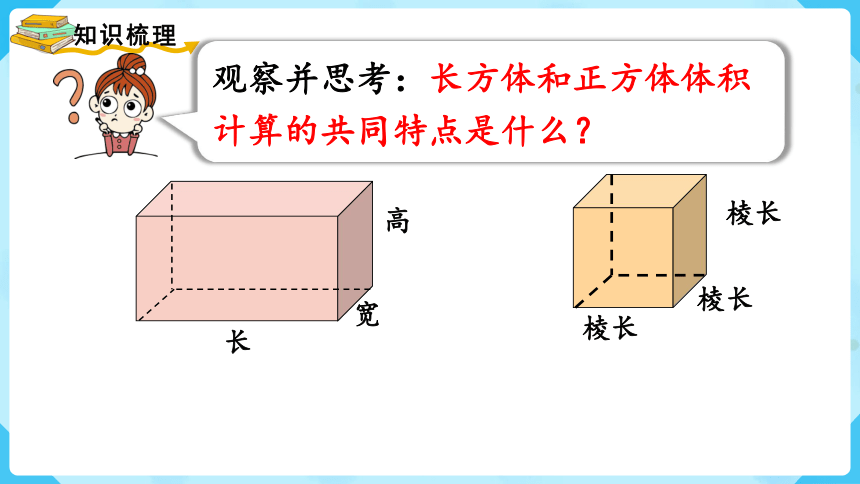
观察并思考:长方体和正方体体积计算的共同特点是什么?
棱长
棱长
棱长
长
高
宽
知识梳理
棱长
棱长
棱长
长
高
宽
正方体的体积=棱长×棱长×棱长
长方体的体积=长×宽×高
底面积
底面积
知识梳理
棱长
棱长
棱长
长
高
宽
如果用字母S表示底面积,上面的公式可以写成:
V = S h
长方体(或正方体)的体积=底面积×高
一根长方体木料,长5米,横截面的面积是0.06平方米,这根木料的体积是多少立方分米?
0.06平方米
5米
长方体(或正方体)的体积=底面积×高
0.06×5=0.3(立方米)
答:这根木料的体积是300立方分米。
典例精析
0.3立方米=300立方分米
拓展运用
一根长20dm的长方体木料,将它截成3段后,表面积增加36dm2,原来这根木料的体积是多少立方分米?
横截面积:36÷4=9 (dm2)
答:原来这根木料的体积是180 dm3。
木料体积:9×20=180 (dm3)
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
复习回顾:圆柱的体积
知识梳理
你还记得圆柱的体积公式是如何推导的吗?
学生展示
长方体的体积
圆柱的体积
= 底面积 × 高
= 底面积 × 高
圆柱的体积公式
原来是这样推导的
复习回顾:圆柱的体积
知识梳理
圆柱的体积=底面积×高
圆柱的体积:V=πr2h
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
复习回顾:圆锥的体积
知识梳理
把圆锥形容器里的水倒入与它等底、等高的圆柱形容器内,( )次才能倒满。
复习回顾:圆锥的体积
知识梳理
把圆锥形容器里的水倒入与它等底、等高的圆柱形容器内,( )次才能倒满。
3
复习回顾:圆锥的体积
知识梳理
圆锥的体积=-×底面积×高
13
V=-Sh=-πr2h
13
13
=- ×
13
圆锥的体积:
体积=-×底面积×高
13
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
典例精析
计算下面这个立体图形的体积是多少?
(单位:cm3)
4÷2 = 2 (cm)
3.14×22×7= 87.92(cm3)
87.92 + 12.56 =100.48(cm3)
×3.14×22×3= 12.56(cm3)
圆柱:
圆锥:
拓展运用
如下图,这个三角形以 4 cm 的直角边所在直线为轴快速旋转一周,得到的圆锥的体积是( )cm3。
B
A、12.56 B、37.68
C、50.24 D、113.04
体积=-×底面积×高
13
立体图形的
体积
长方体
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
立体图形的体积
——整理与复习
拓展运用
1、(1)把一个长10厘米,宽8厘米,高是6厘米的长方体木块,加工成一个最大的正方体,削掉的体积是多少立方厘米
6×6×6=216(cm3)
10×8×6=480(cm3)
480-216=264(cm3)
答:削掉的体积是264 cm3。
1、(2)把这个棱长是6厘米的正方体木块,加工成一个最大圆柱体,圆柱的体积是多少立方厘米
3.14×(6÷2)2=28.26(cm2)
28.26×6 =169.56(cm3)
拓展运用
答:圆柱的体积是169.56立方厘米。
1、(3)把这个圆柱体木块,加工成一个最大圆锥体,削掉的体积是多少立方厘米
169.56× =113.04(cm3)
23
拓展运用
答:削掉的体积是113.04 cm3。
2、如图,将乙水缸中的水全部倒入甲水缸中,这时甲水缸中的水深多少厘米?
628÷78.5 =8(cm)
=
圆柱形水缸中水的体积
长方体水缸中水的体积
10×10×6.28 = 628(cm3)
3.14×5 = 78.5(cm2)
答:这时甲水缸中的水深8cm。
拓展运用
课堂小结
通过这节课的学习,
你有什么收获
体积=-×底面积×高
13
立体图形的
体积
长方体
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
课堂总结
立体图形的体积
——整理与复习
课堂小结
通过这节课的学习,
你有什么收获
2.怎样测量出一块拳头大的鹅卵石的体积?
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
还记得求不规则物体体积的方法吗?
教材第87页“做一做”第1题
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
50× 30 ×10.4 - 15000 =600(cm3)
答:鱼的体积是 600 cm3。
15 L = 15000 cm3
一个圆柱形水槽,从里面量得底面直径是40 cm,高是30 cm。水槽中盛有一些水,把一个底面半径为 10 cm的圆锥浸没在水槽中,水面上升了 2 cm且水未溢出。求这个圆锥的高?
拓展运用
答:这个圆锥的高是 24 cm。
3.14×(40÷2)2×2=2512(cm3)
2512÷( ×3.14×102 ) =24(cm)
3、一个正方体铁块,棱长是4分米。把它熔铸成一个长为8分米,宽为2分米的长方体,问这个长方体的高是多少分米?
拓展运用
捏橡皮泥、钢铁铸造
体积不变
4×4×4=64(立方分米)
64÷8÷2=4(分米)
答:这个长方体的高是 4 分米。
立体图形的体积
——整理与复习
义务教育人教版六年级下册
知识梳理
回忆一下,小学阶段我们学过的立体图形有哪些?
你能说一说吗?
复习导入
立体图形 表面积 计算公式
S=2(ab+ah+bh)
S=a×a× 6 = 6a2
S=2πrh+2πr2
复习回顾:
1、立体图形的表面积和体积有什么区别呢?
2、什么是表面积? 什么是体积?
知识梳理
同桌讨论,总结汇报。
知识梳理
一个立体图形所有面的面积总和,叫做它的表面积。
一个立体图形所占空间的大小,叫做它的体积。
复习回顾:
1、立体图形的表面积和体积有什么区别呢?
2、什么是表面积? 什么是体积?
1
2
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
复习回顾:长方体的体积
知识梳理
长方体的体积=长×宽×高
长
高
宽
长方体的体积:V=abh
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
复习回顾:正方体的体积
知识梳理
棱长
棱长
棱长
长
高
宽
正方体是特殊的长方体,
是长、宽、高都相等的长方体。
复习回顾:正方体的体积
知识梳理
正方体的体积=棱长×棱长×棱长
棱长
棱长
棱长
长
高
宽
长方体的体积=长×宽×高
复习回顾:正方体的体积
知识梳理
正方体的体积=棱长×棱长×棱长
棱长
棱长
棱长
长
高
宽
正方体的体积:V= a×a×a = a3
知识梳理
观察并思考:长方体和正方体体积计算的共同特点是什么?
棱长
棱长
棱长
长
高
宽
知识梳理
棱长
棱长
棱长
长
高
宽
正方体的体积=棱长×棱长×棱长
长方体的体积=长×宽×高
底面积
底面积
知识梳理
棱长
棱长
棱长
长
高
宽
如果用字母S表示底面积,上面的公式可以写成:
V = S h
长方体(或正方体)的体积=底面积×高
一根长方体木料,长5米,横截面的面积是0.06平方米,这根木料的体积是多少立方分米?
0.06平方米
5米
长方体(或正方体)的体积=底面积×高
0.06×5=0.3(立方米)
答:这根木料的体积是300立方分米。
典例精析
0.3立方米=300立方分米
拓展运用
一根长20dm的长方体木料,将它截成3段后,表面积增加36dm2,原来这根木料的体积是多少立方分米?
横截面积:36÷4=9 (dm2)
答:原来这根木料的体积是180 dm3。
木料体积:9×20=180 (dm3)
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
复习回顾:圆柱的体积
知识梳理
你还记得圆柱的体积公式是如何推导的吗?
学生展示
长方体的体积
圆柱的体积
= 底面积 × 高
= 底面积 × 高
圆柱的体积公式
原来是这样推导的
复习回顾:圆柱的体积
知识梳理
圆柱的体积=底面积×高
圆柱的体积:V=πr2h
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
复习回顾:圆锥的体积
知识梳理
把圆锥形容器里的水倒入与它等底、等高的圆柱形容器内,( )次才能倒满。
复习回顾:圆锥的体积
知识梳理
把圆锥形容器里的水倒入与它等底、等高的圆柱形容器内,( )次才能倒满。
3
复习回顾:圆锥的体积
知识梳理
圆锥的体积=-×底面积×高
13
V=-Sh=-πr2h
13
13
=- ×
13
圆锥的体积:
体积=-×底面积×高
13
立体图形的
体积
长方体
知识梳理
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
典例精析
计算下面这个立体图形的体积是多少?
(单位:cm3)
4÷2 = 2 (cm)
3.14×22×7= 87.92(cm3)
87.92 + 12.56 =100.48(cm3)
×3.14×22×3= 12.56(cm3)
圆柱:
圆锥:
拓展运用
如下图,这个三角形以 4 cm 的直角边所在直线为轴快速旋转一周,得到的圆锥的体积是( )cm3。
B
A、12.56 B、37.68
C、50.24 D、113.04
体积=-×底面积×高
13
立体图形的
体积
长方体
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
立体图形的体积
——整理与复习
拓展运用
1、(1)把一个长10厘米,宽8厘米,高是6厘米的长方体木块,加工成一个最大的正方体,削掉的体积是多少立方厘米
6×6×6=216(cm3)
10×8×6=480(cm3)
480-216=264(cm3)
答:削掉的体积是264 cm3。
1、(2)把这个棱长是6厘米的正方体木块,加工成一个最大圆柱体,圆柱的体积是多少立方厘米
3.14×(6÷2)2=28.26(cm2)
28.26×6 =169.56(cm3)
拓展运用
答:圆柱的体积是169.56立方厘米。
1、(3)把这个圆柱体木块,加工成一个最大圆锥体,削掉的体积是多少立方厘米
169.56× =113.04(cm3)
23
拓展运用
答:削掉的体积是113.04 cm3。
2、如图,将乙水缸中的水全部倒入甲水缸中,这时甲水缸中的水深多少厘米?
628÷78.5 =8(cm)
=
圆柱形水缸中水的体积
长方体水缸中水的体积
10×10×6.28 = 628(cm3)
3.14×5 = 78.5(cm2)
答:这时甲水缸中的水深8cm。
拓展运用
课堂小结
通过这节课的学习,
你有什么收获
体积=-×底面积×高
13
立体图形的
体积
长方体
1、
2、
3、
4、
正方体
圆 柱
圆 锥
体积=长×宽×高
体积=棱长×棱长×棱长
体积=底面积×高
课堂总结
立体图形的体积
——整理与复习
课堂小结
通过这节课的学习,
你有什么收获
2.怎样测量出一块拳头大的鹅卵石的体积?
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
还记得求不规则物体体积的方法吗?
教材第87页“做一做”第1题
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
50× 30 ×10.4 - 15000 =600(cm3)
答:鱼的体积是 600 cm3。
15 L = 15000 cm3
一个圆柱形水槽,从里面量得底面直径是40 cm,高是30 cm。水槽中盛有一些水,把一个底面半径为 10 cm的圆锥浸没在水槽中,水面上升了 2 cm且水未溢出。求这个圆锥的高?
拓展运用
答:这个圆锥的高是 24 cm。
3.14×(40÷2)2×2=2512(cm3)
2512÷( ×3.14×102 ) =24(cm)
3、一个正方体铁块,棱长是4分米。把它熔铸成一个长为8分米,宽为2分米的长方体,问这个长方体的高是多少分米?
拓展运用
捏橡皮泥、钢铁铸造
体积不变
4×4×4=64(立方分米)
64÷8÷2=4(分米)
答:这个长方体的高是 4 分米。
同课章节目录
