五年级下册数学人教版《总复习——长方体和正方体》课件(共28张PPT)
文档属性
| 名称 | 五年级下册数学人教版《总复习——长方体和正方体》课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
总复习——图形与几何
长方体和正方体
这学期我们学了哪些和“图形与几何”有关的内容?在哪个单元学的呢?
1.由 ______ 个长方形(特殊情况有两个相对的面是______)围成的立体图形叫做长方体。2.两个面相交的边叫做 ______ 。三条棱相交的点叫做 ______。3.相交于一个顶点的三条棱的长度分别叫做长方体的 。4.判断:长方体的三条棱分别叫做长方体的长宽高。( )
回顾旧知(长方体相关知识)
6
正方形
棱
顶点
长、宽、高
×
●长方体特点:5.有_____个面 (6个面都是______或者4个面是______,2个面是______),______个顶点,______条棱,相对的面的______,相对的棱的______。6.一个长方体(不含正方体)最多有______个面是长方形,最少有______个面是长方形,最多有______个面是正方形。最多有______个面完全相同。7.长方体12条棱可以分成3组,分别有______。
回顾旧知(长方体相关知识)
6
长方形
长方形
正方形
8
12
面积相等
长度相等
6
4
2
4
4条长、4条宽、4条高
回顾旧知(正方体相关知识)
●正方体特点:
8.正方体有______条棱,它们的长度都______。有______个顶点。
9.正方体可以说是长、宽、高都______的长方体,它是一种特殊的______。
12
相等
8
相等
长方体
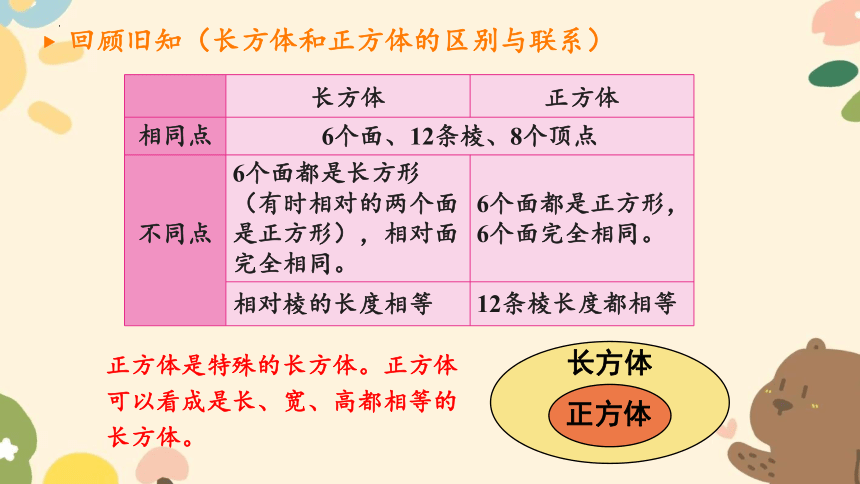
回顾旧知(长方体和正方体的区别与联系)
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同。
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。正方体可以看成是长、宽、高都相等的长方体。
长方体
正方体
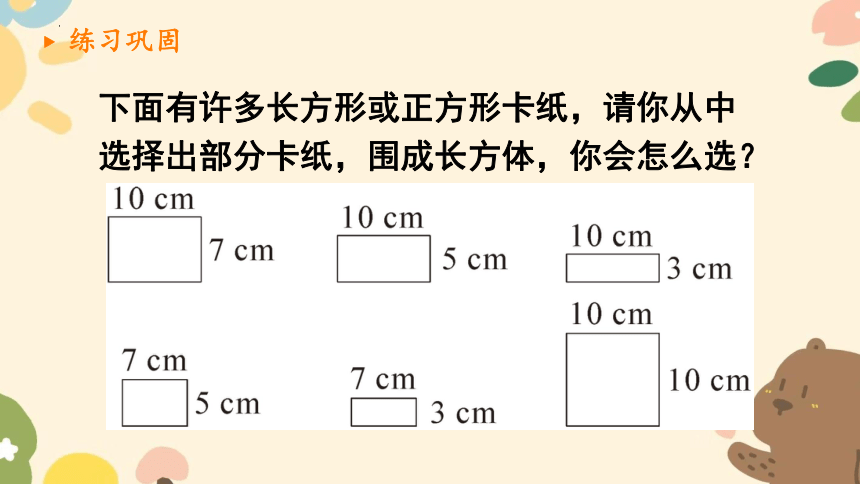
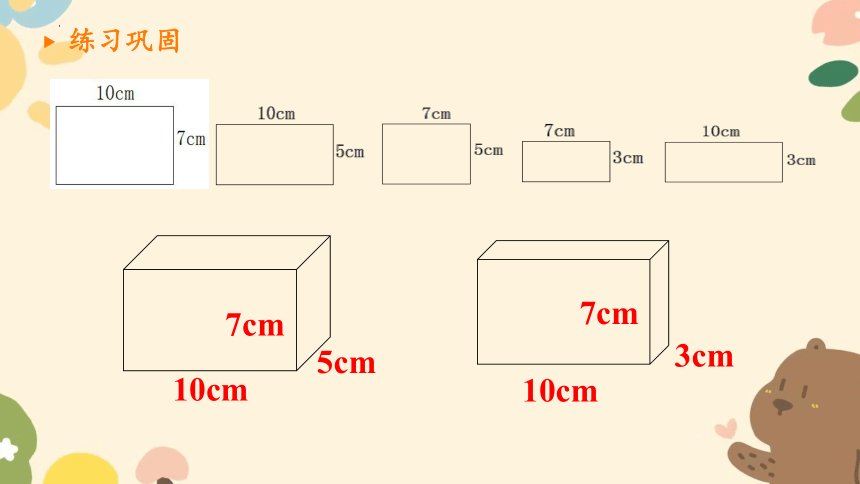
练习巩固
下面有许多长方形或正方形卡纸,请你从中选择出部分卡纸,围成长方体,你会怎么选?
10cm
7cm
5cm
10cm
7cm
3cm
练习巩固
●长方体、正方体有关棱长计算公式:
10.长方体的棱长总和= 。
11.已知长方体的棱长之和,求长方体的长= ;宽= ;高= 。
12.正方体的棱长总和= ;正方体的棱长= ;(用字母表示)
回顾旧知(长方体和正方体的棱长)
(a+b+h)×4
L÷4-b-h
L÷4-a-h
L÷4-a-b
a×12
L÷12
回顾旧知(长方体和正方体的表面积)
●表面积的计算方法:
13.长方体表面积= ;(用字母表示)
14.无底(或无盖)长方体表面积= ;(用字母表示)
15.无底又无盖长方体表面积= ;(用字母表示)
16.正方体的表面积= ;(用字母表示)
2(ab+ah+bh)
2(ah+bh)+ab
2(ah+bh)
a×a×6 或 6a
17.油箱、罐头盒等都是______个面;游泳池、鱼缸等都只有______个面;水管、烟囱等都只有______个面。
18.用刀分开物体时,每分一次增加______个面,表面积= (用字母表示)。
19.一根长方体木料,长1.5米,宽和厚都是2分米,把它锯成4段,表面积最少增加______平方分米。
36.把长方体或正方体截成若干个小长方体(或正方体)后,______增加了,______不变。
拓展巩固
6
5
4
2
相应增加
24
表面积
体积
拓展巩固
20.长方体或正方体的长、宽、高同时扩大(或缩小)几倍,表面积会扩大(或缩小)倍数的_____。体积会扩大(或缩小)倍数的_____。
21.长、宽、高各扩大3倍,表面积就会扩大到原来的___倍,体积就会扩大到原来的____倍。
22.长、宽、高各缩小3倍,表面积就会缩小到原来的____,体积就会扩大到原来的______。
平方倍
立方倍
9
27
回顾旧知(长方体和正方体的体积)
●长方体和正方体的体积:
(1)体积的意义: ________________________叫做物体的体积。
(2)体积单位: ______、______、______;用字母表示为______、______、______。
体积相邻单位间的进率是: ______。
物体所占空间的大小
立方米
立方分米
立方厘米
m
dm
cm
1000
回顾旧知(长方体和正方体的体积)
23.长方体的体积= ;(用字母表示)
24.知道体积,长方体的长= ;宽= ;高= 。(用字母表示)
25.正方体的体积= ______;表示3个a ______。
26.长方体或正方体底面的面积叫做______。(横截面积相当于______,长相当于 ______ )。
abh
V÷b÷h
V÷a÷h
V÷a÷b
a×a×a=a
相乘
底面积
底面积
高
回顾旧知(长方体和正方体的容积)
27.箱子、油桶、仓库等(容器)所能容纳物体的 ______ ,通常叫做他们的容积。
28.计量容积,一般就用单位。计量液体的体积,如水、油等,单位升或毫升,常用的容积单位有____和______,也可以写成____和______。
29.1升= ______ 立方分米;1毫升= ______ 立方厘米;1升= ______ 毫升。
30.长方体或正方体容器容积的计算方法,跟体积的计算方法相同。但要从量长、宽、高。所以,对于同一个物体,体积______ 容积。(填“>”或“<”)
体积
升
毫升
L
mL
1
1
1000
>
综合应用
1. 说一说,下面的问题与哪些知识有关?
①给房间的地面铺瓷砖。
②仓库所占的空间有多大。
③运动场上的沙坑占地面积是多少。
④做一个纸盒需要多大的纸板。
⑤运动会上明明参加400米赛跑的距离。
⑥冰箱里面能装东西的多少。
⑦铺一个沙坑需要多少沙。
面积
体积
面积
表面积
长度
容积
容积或体积
练习巩固(书119页第11题)
11. (1)举例说明1cm 、1dm 、1m 各有多
大,1L、1mL的水大约有多少。
1cm
1dm
1m
1L
大约20滴水
回顾旧知(进率)
31.长度单位:1米=______分米=______厘米=______毫米;(长度相邻单位进率______)
1千米= ______ 米
32.面积单位:1平方米= ______平方分米= ______平方厘米;(面积相邻单位进率是______)
1平方千米= ______公顷= ______平方米
33.体积单位:1立方米= ______立方分米= ______立方厘米;(体积相邻单位进率是______)
34.容积单位:1立方分米= ______立方厘米;1立方厘米= ______毫升;1升= ______毫升;
35.质量单位:1吨= ______千克1千克= ______克
10
100
1000
10
1000
100
10000
100
100
1000000
1000
1000000
1000
1000
1
1000
1000
1000
练习巩固(书119页第11题)
11. (2)
1m =____dm
700dm =____m
81cm =____mL
1L=____dm
2.3dm =____cm
560mL=____L
练习巩固(填上合适的单位)
米
立方米
平方米
毫升
立方厘米
立方米
毫升
立方分米
毫升
立方分米
立方米
升
立方米
平方米
升
厘米
平方米
平方分米
平方厘米
升
立方厘米
综合应用(书120页第13题)
13. 一块长方形铁皮(如右图),
从四个角各切掉一个边长
5cm的正方形,然后做成无盖盒子。这个盒子用了多少铁皮?它的容积有多大?
综合应用(书120页第14题)
7. 一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果竖直放入一块棱长为4dm的正方体铁块,缸里的水会溢出多少升?
如何利用排水法计算物体体积?
回顾旧知(排水法)
V物=V总-V水
知道总体积和原来水的体积:
知道水缸的长宽高和水上升的高度:
V物=水上升的高×长×宽
V物=水上升的高×底面积
回顾旧知(排水法)
水满:
溢出水的体积=物品体积
水未满:
溢出水的体积=物品体积-缸中剩余体积
综合应用(书120页第14题)
7. 一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果竖直放入一块棱长为4dm的正方体铁块,缸里的水会溢出多少升?
综合应用(书120页第17题)
17.北京2022年冬奥会和冬残奥会上,国家游泳中心“水立方”完美化身为“冰立方”,成为世界首座完成“水冰转换”的奥运场馆。作为冰壶比赛的场馆,“冰立方”改造出4条达到国际最高标准的冰壶赛道,每条赛道长44.5 m,宽4.32 m。由于冰壶比赛对冰面的要求非常高,所以必须经过多次细致的洒水,赛道上厚度约为80 mm的冰层才能完美地呈现出来。你知道大约需要洒多少升水吗 (0.9L水可以转化为1L的冰。用计算器计算。)
44.5m=445dm 4.32m=43.2dm 80mm=0.8dm
55365.12 dm3=55365.12 L
答:要洒55365.12 L水。
综合应用(书120页第17题)
课堂小结
总复习——图形与几何
长方体和正方体
这学期我们学了哪些和“图形与几何”有关的内容?在哪个单元学的呢?
1.由 ______ 个长方形(特殊情况有两个相对的面是______)围成的立体图形叫做长方体。2.两个面相交的边叫做 ______ 。三条棱相交的点叫做 ______。3.相交于一个顶点的三条棱的长度分别叫做长方体的 。4.判断:长方体的三条棱分别叫做长方体的长宽高。( )
回顾旧知(长方体相关知识)
6
正方形
棱
顶点
长、宽、高
×
●长方体特点:5.有_____个面 (6个面都是______或者4个面是______,2个面是______),______个顶点,______条棱,相对的面的______,相对的棱的______。6.一个长方体(不含正方体)最多有______个面是长方形,最少有______个面是长方形,最多有______个面是正方形。最多有______个面完全相同。7.长方体12条棱可以分成3组,分别有______。
回顾旧知(长方体相关知识)
6
长方形
长方形
正方形
8
12
面积相等
长度相等
6
4
2
4
4条长、4条宽、4条高
回顾旧知(正方体相关知识)
●正方体特点:
8.正方体有______条棱,它们的长度都______。有______个顶点。
9.正方体可以说是长、宽、高都______的长方体,它是一种特殊的______。
12
相等
8
相等
长方体
回顾旧知(长方体和正方体的区别与联系)
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同。
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。正方体可以看成是长、宽、高都相等的长方体。
长方体
正方体
练习巩固
下面有许多长方形或正方形卡纸,请你从中选择出部分卡纸,围成长方体,你会怎么选?
10cm
7cm
5cm
10cm
7cm
3cm
练习巩固
●长方体、正方体有关棱长计算公式:
10.长方体的棱长总和= 。
11.已知长方体的棱长之和,求长方体的长= ;宽= ;高= 。
12.正方体的棱长总和= ;正方体的棱长= ;(用字母表示)
回顾旧知(长方体和正方体的棱长)
(a+b+h)×4
L÷4-b-h
L÷4-a-h
L÷4-a-b
a×12
L÷12
回顾旧知(长方体和正方体的表面积)
●表面积的计算方法:
13.长方体表面积= ;(用字母表示)
14.无底(或无盖)长方体表面积= ;(用字母表示)
15.无底又无盖长方体表面积= ;(用字母表示)
16.正方体的表面积= ;(用字母表示)
2(ab+ah+bh)
2(ah+bh)+ab
2(ah+bh)
a×a×6 或 6a
17.油箱、罐头盒等都是______个面;游泳池、鱼缸等都只有______个面;水管、烟囱等都只有______个面。
18.用刀分开物体时,每分一次增加______个面,表面积= (用字母表示)。
19.一根长方体木料,长1.5米,宽和厚都是2分米,把它锯成4段,表面积最少增加______平方分米。
36.把长方体或正方体截成若干个小长方体(或正方体)后,______增加了,______不变。
拓展巩固
6
5
4
2
相应增加
24
表面积
体积
拓展巩固
20.长方体或正方体的长、宽、高同时扩大(或缩小)几倍,表面积会扩大(或缩小)倍数的_____。体积会扩大(或缩小)倍数的_____。
21.长、宽、高各扩大3倍,表面积就会扩大到原来的___倍,体积就会扩大到原来的____倍。
22.长、宽、高各缩小3倍,表面积就会缩小到原来的____,体积就会扩大到原来的______。
平方倍
立方倍
9
27
回顾旧知(长方体和正方体的体积)
●长方体和正方体的体积:
(1)体积的意义: ________________________叫做物体的体积。
(2)体积单位: ______、______、______;用字母表示为______、______、______。
体积相邻单位间的进率是: ______。
物体所占空间的大小
立方米
立方分米
立方厘米
m
dm
cm
1000
回顾旧知(长方体和正方体的体积)
23.长方体的体积= ;(用字母表示)
24.知道体积,长方体的长= ;宽= ;高= 。(用字母表示)
25.正方体的体积= ______;表示3个a ______。
26.长方体或正方体底面的面积叫做______。(横截面积相当于______,长相当于 ______ )。
abh
V÷b÷h
V÷a÷h
V÷a÷b
a×a×a=a
相乘
底面积
底面积
高
回顾旧知(长方体和正方体的容积)
27.箱子、油桶、仓库等(容器)所能容纳物体的 ______ ,通常叫做他们的容积。
28.计量容积,一般就用单位。计量液体的体积,如水、油等,单位升或毫升,常用的容积单位有____和______,也可以写成____和______。
29.1升= ______ 立方分米;1毫升= ______ 立方厘米;1升= ______ 毫升。
30.长方体或正方体容器容积的计算方法,跟体积的计算方法相同。但要从量长、宽、高。所以,对于同一个物体,体积______ 容积。(填“>”或“<”)
体积
升
毫升
L
mL
1
1
1000
>
综合应用
1. 说一说,下面的问题与哪些知识有关?
①给房间的地面铺瓷砖。
②仓库所占的空间有多大。
③运动场上的沙坑占地面积是多少。
④做一个纸盒需要多大的纸板。
⑤运动会上明明参加400米赛跑的距离。
⑥冰箱里面能装东西的多少。
⑦铺一个沙坑需要多少沙。
面积
体积
面积
表面积
长度
容积
容积或体积
练习巩固(书119页第11题)
11. (1)举例说明1cm 、1dm 、1m 各有多
大,1L、1mL的水大约有多少。
1cm
1dm
1m
1L
大约20滴水
回顾旧知(进率)
31.长度单位:1米=______分米=______厘米=______毫米;(长度相邻单位进率______)
1千米= ______ 米
32.面积单位:1平方米= ______平方分米= ______平方厘米;(面积相邻单位进率是______)
1平方千米= ______公顷= ______平方米
33.体积单位:1立方米= ______立方分米= ______立方厘米;(体积相邻单位进率是______)
34.容积单位:1立方分米= ______立方厘米;1立方厘米= ______毫升;1升= ______毫升;
35.质量单位:1吨= ______千克1千克= ______克
10
100
1000
10
1000
100
10000
100
100
1000000
1000
1000000
1000
1000
1
1000
1000
1000
练习巩固(书119页第11题)
11. (2)
1m =____dm
700dm =____m
81cm =____mL
1L=____dm
2.3dm =____cm
560mL=____L
练习巩固(填上合适的单位)
米
立方米
平方米
毫升
立方厘米
立方米
毫升
立方分米
毫升
立方分米
立方米
升
立方米
平方米
升
厘米
平方米
平方分米
平方厘米
升
立方厘米
综合应用(书120页第13题)
13. 一块长方形铁皮(如右图),
从四个角各切掉一个边长
5cm的正方形,然后做成无盖盒子。这个盒子用了多少铁皮?它的容积有多大?
综合应用(书120页第14题)
7. 一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果竖直放入一块棱长为4dm的正方体铁块,缸里的水会溢出多少升?
如何利用排水法计算物体体积?
回顾旧知(排水法)
V物=V总-V水
知道总体积和原来水的体积:
知道水缸的长宽高和水上升的高度:
V物=水上升的高×长×宽
V物=水上升的高×底面积
回顾旧知(排水法)
水满:
溢出水的体积=物品体积
水未满:
溢出水的体积=物品体积-缸中剩余体积
综合应用(书120页第14题)
7. 一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果竖直放入一块棱长为4dm的正方体铁块,缸里的水会溢出多少升?
综合应用(书120页第17题)
17.北京2022年冬奥会和冬残奥会上,国家游泳中心“水立方”完美化身为“冰立方”,成为世界首座完成“水冰转换”的奥运场馆。作为冰壶比赛的场馆,“冰立方”改造出4条达到国际最高标准的冰壶赛道,每条赛道长44.5 m,宽4.32 m。由于冰壶比赛对冰面的要求非常高,所以必须经过多次细致的洒水,赛道上厚度约为80 mm的冰层才能完美地呈现出来。你知道大约需要洒多少升水吗 (0.9L水可以转化为1L的冰。用计算器计算。)
44.5m=445dm 4.32m=43.2dm 80mm=0.8dm
55365.12 dm3=55365.12 L
答:要洒55365.12 L水。
综合应用(书120页第17题)
课堂小结
