人教版数学九年级下册 26.1.2反比例函数的图象与性质 课件(共25张PPT)
文档属性
| 名称 | 人教版数学九年级下册 26.1.2反比例函数的图象与性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 613.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 08:00:39 | ||
图片预览







文档简介
(共25张PPT)
第2课 反比例函数的图象与性质(1)
学习目标:
1.会用描点法画出反比例函数的图象,归纳得到反比例函数的图象特征和性质.
2.在类比探究中,体会“分类讨论”“数形结合”“从特殊到一般”的数学思想.
学习重点:
由反比例函数的图象,并结合解析式,探究反比例函数的性质.
回顾旧知
1.上节课我们学的反比例函数解析式是什么?
3.反比例函数的三种常见形式是什么?
2.其中自变量x的取值范围是什么?函数y的取值范围是什么?
问题:
1.一次函数y=kx+b(k≠0)的图象是一条___________,
2.二次函数 的图象是一条________,
直线
抛物线
3.反比例函数 的图象是什么样呢?
我们用什么方法画反比例函数的图象呢?
根据k的正负不同,应该如何分类讨论呢?
问题引入
如何探究正比例函数的图象和性质?
?
探究方法:
O
O
分类讨论
O
k>0
k<0
k>0
k<0
例 画出反比例函数 与 的图象.
函数图象画法
列
表
描
点
连
线
描点法
新知探究1:反比例函数 的图象
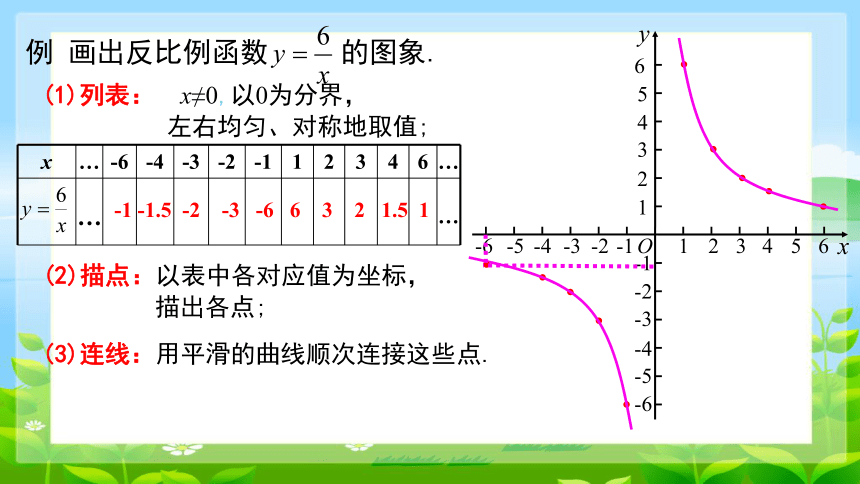
例 画出反比例函数 的图象.
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
… …
-1 -1.5 -2 -3 -6 6 3 2 1.5 1
(3)连线:用平滑的曲线顺次连接这些点.
(1)列表: x≠0,以0为分界,
左右均匀、对称地取值;
(2)描点:以表中各对应值为坐标,
描出各点;
y
-1
O
-2
5
6
x
4
3
2
1
1
2
3
4
5
6
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
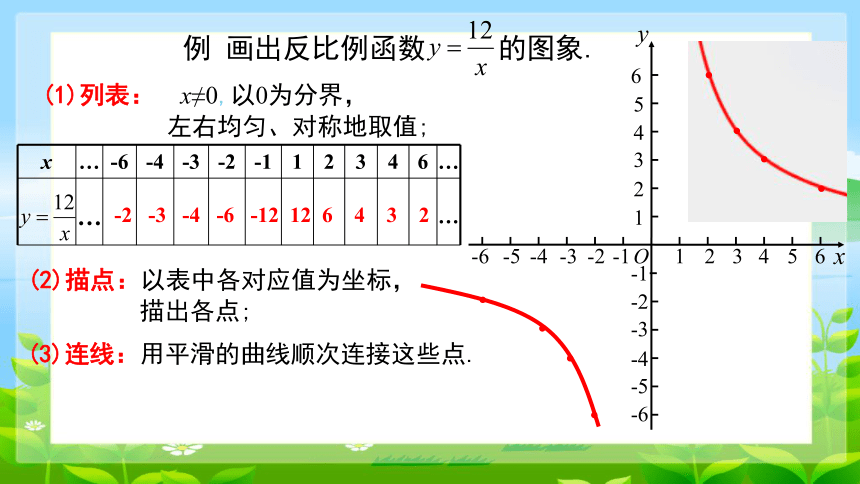
-2 -3 -4 -6 -12 12 6 4 3 2
(3)连线:用平滑的曲线顺次连接这些点.
(2)描点:以表中各对应值为坐标,
描出各点;
-1
O
-2
5
6
x
4
3
2
1
1
2
3
4
5
6
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
y
(1)列表: x≠0,以0为分界,
左右均匀、对称地取值;
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
… …
例 画出反比例函数 的图象.
https://www./calculator/6jrc1fqea1
函数关系式 k 图象 形状 位置 变化趋势
k > 0
第一、
第三象限
双曲线
k < 0
在每一个象限内,
y随x的增大而减小.
k的正负决定反比例函数所在的象限和变化趋势.
双曲线
第二、
第四象限
在每一个象限内,
y随x的增大而增大.
归纳:
课堂练习
1.下列图象中可能是反比例函数图象的是( ).
(A) (B) (C) (D)
C
双曲线
直线
抛物线
直线
2.如图所示的图象对应的函数解析式可能为( ).
C
课堂练习
双曲线
第一、第三象限
k>0
(A) y=5x (B) y=2x+3 (C) (D)
反比例函数
3.填空:
(1)反比例函数 的图象在___________象限.
第一、第三
>0
课堂练习
<
增大
课堂练习
3.填空:
(2) 已知反比例函数的图象如图所示,则k 0,且 在图象的每一支上, 随 的增大而 .
4.已知反比例函数 的图象过点A(2,1),则它的图象位于___________象限,且k______0.
第一、第三
>
课堂练习
第一象限
3. (1)反比例函数y= 的图象在________象限,在每一个象限内,y随x的增大而______;
(2)反比例函数y=- 的图象在________象限,在每个象限内,y随x的增大而________.
第一、三
反比例函数的图象与性质
减小
第二、四
增大
4. (1)函数y= 的图象在第一、三象限内,则k的取值范围是_______;
(2)双曲线y= 的图象有一支在第四象限,则k的取值范围是_________.
k>1
k<-3
5.若点A(x1,y1),B(x2,y2)在反比例函数 的图象上,
且x1(A) y1y2
(C) y1=y2 (D) 不能确定
A
图象 变化趋势
6.反比例函数y= 的图象是_____线,图象在_________象限,在每一支上,y随x的增大而_____.
7.已知点P(1,-3)在反比例函数y= (k≠0)的图象上,则k的值是 ( )
A.3 B.-3
C. D.
双曲
第一、三
减小
B
课堂练习
8. 反比例函数y= ,当x>0时,y随x的增大而增大,则k的取值范围是______.
9. 写出一个反比例函数,使得它的图象在第二、四象限:___________________________.
方法一:
画出反比例函数 的图象,找到横坐标分别为-1,4的两个点,比较其纵坐标的大小.(位置高低)
数形结合
10. 已知点A(-1,y1),B(4,y2)都在反比例函数 的图象上,
则y1与y2的大小关系(从大到小)为 .
y2>y1
解:将x=-1,4分别代数函数解析式,求出
y1=-4,y2=1, 进而比较出y2>y1.
方法二:
11.【原创题】在同一直角坐标系中,直线y=x+1与双曲线y= 的交点个数为 ( )
A.0个
B.1个
C.2个
D.3个
C
12.【易错题】在同一平面直角坐标系中,函数y=kx-k与y= (k<0)的大致图象是 ( ) ( ) ( )
B
13.【原创题】如图,⊙A和⊙B都与x轴和y轴相切,⊙A与⊙B都在反比例函数y=- 的图象上,则图中阴影部分的面积为_____.
π
本节课你学到了什么?
1.画反比例函数 的图象.
2.反比例函数的图象特征和性质.
数学思想方法
分类讨论
数形结合
从特殊到一般
①形状
②位置
③变化趋势
课堂小结
第2课 反比例函数的图象与性质(1)
学习目标:
1.会用描点法画出反比例函数的图象,归纳得到反比例函数的图象特征和性质.
2.在类比探究中,体会“分类讨论”“数形结合”“从特殊到一般”的数学思想.
学习重点:
由反比例函数的图象,并结合解析式,探究反比例函数的性质.
回顾旧知
1.上节课我们学的反比例函数解析式是什么?
3.反比例函数的三种常见形式是什么?
2.其中自变量x的取值范围是什么?函数y的取值范围是什么?
问题:
1.一次函数y=kx+b(k≠0)的图象是一条___________,
2.二次函数 的图象是一条________,
直线
抛物线
3.反比例函数 的图象是什么样呢?
我们用什么方法画反比例函数的图象呢?
根据k的正负不同,应该如何分类讨论呢?
问题引入
如何探究正比例函数的图象和性质?
?
探究方法:
O
O
分类讨论
O
k>0
k<0
k>0
k<0
例 画出反比例函数 与 的图象.
函数图象画法
列
表
描
点
连
线
描点法
新知探究1:反比例函数 的图象
例 画出反比例函数 的图象.
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
… …
-1 -1.5 -2 -3 -6 6 3 2 1.5 1
(3)连线:用平滑的曲线顺次连接这些点.
(1)列表: x≠0,以0为分界,
左右均匀、对称地取值;
(2)描点:以表中各对应值为坐标,
描出各点;
y
-1
O
-2
5
6
x
4
3
2
1
1
2
3
4
5
6
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
-2 -3 -4 -6 -12 12 6 4 3 2
(3)连线:用平滑的曲线顺次连接这些点.
(2)描点:以表中各对应值为坐标,
描出各点;
-1
O
-2
5
6
x
4
3
2
1
1
2
3
4
5
6
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
y
(1)列表: x≠0,以0为分界,
左右均匀、对称地取值;
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
… …
例 画出反比例函数 的图象.
https://www./calculator/6jrc1fqea1
函数关系式 k 图象 形状 位置 变化趋势
k > 0
第一、
第三象限
双曲线
k < 0
在每一个象限内,
y随x的增大而减小.
k的正负决定反比例函数所在的象限和变化趋势.
双曲线
第二、
第四象限
在每一个象限内,
y随x的增大而增大.
归纳:
课堂练习
1.下列图象中可能是反比例函数图象的是( ).
(A) (B) (C) (D)
C
双曲线
直线
抛物线
直线
2.如图所示的图象对应的函数解析式可能为( ).
C
课堂练习
双曲线
第一、第三象限
k>0
(A) y=5x (B) y=2x+3 (C) (D)
反比例函数
3.填空:
(1)反比例函数 的图象在___________象限.
第一、第三
>0
课堂练习
<
增大
课堂练习
3.填空:
(2) 已知反比例函数的图象如图所示,则k 0,且 在图象的每一支上, 随 的增大而 .
4.已知反比例函数 的图象过点A(2,1),则它的图象位于___________象限,且k______0.
第一、第三
>
课堂练习
第一象限
3. (1)反比例函数y= 的图象在________象限,在每一个象限内,y随x的增大而______;
(2)反比例函数y=- 的图象在________象限,在每个象限内,y随x的增大而________.
第一、三
反比例函数的图象与性质
减小
第二、四
增大
4. (1)函数y= 的图象在第一、三象限内,则k的取值范围是_______;
(2)双曲线y= 的图象有一支在第四象限,则k的取值范围是_________.
k>1
k<-3
5.若点A(x1,y1),B(x2,y2)在反比例函数 的图象上,
且x1
(C) y1=y2 (D) 不能确定
A
图象 变化趋势
6.反比例函数y= 的图象是_____线,图象在_________象限,在每一支上,y随x的增大而_____.
7.已知点P(1,-3)在反比例函数y= (k≠0)的图象上,则k的值是 ( )
A.3 B.-3
C. D.
双曲
第一、三
减小
B
课堂练习
8. 反比例函数y= ,当x>0时,y随x的增大而增大,则k的取值范围是______.
9. 写出一个反比例函数,使得它的图象在第二、四象限:___________________________.
方法一:
画出反比例函数 的图象,找到横坐标分别为-1,4的两个点,比较其纵坐标的大小.(位置高低)
数形结合
10. 已知点A(-1,y1),B(4,y2)都在反比例函数 的图象上,
则y1与y2的大小关系(从大到小)为 .
y2>y1
解:将x=-1,4分别代数函数解析式,求出
y1=-4,y2=1, 进而比较出y2>y1.
方法二:
11.【原创题】在同一直角坐标系中,直线y=x+1与双曲线y= 的交点个数为 ( )
A.0个
B.1个
C.2个
D.3个
C
12.【易错题】在同一平面直角坐标系中,函数y=kx-k与y= (k<0)的大致图象是 ( ) ( ) ( )
B
13.【原创题】如图,⊙A和⊙B都与x轴和y轴相切,⊙A与⊙B都在反比例函数y=- 的图象上,则图中阴影部分的面积为_____.
π
本节课你学到了什么?
1.画反比例函数 的图象.
2.反比例函数的图象特征和性质.
数学思想方法
分类讨论
数形结合
从特殊到一般
①形状
②位置
③变化趋势
课堂小结
