1.1探索勾股定理(证明)
图片预览

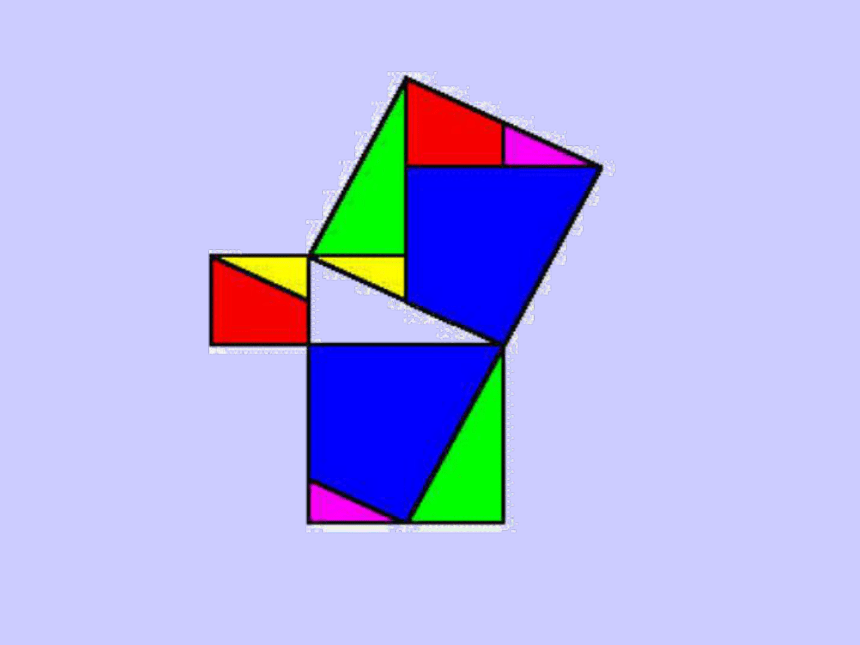

文档简介
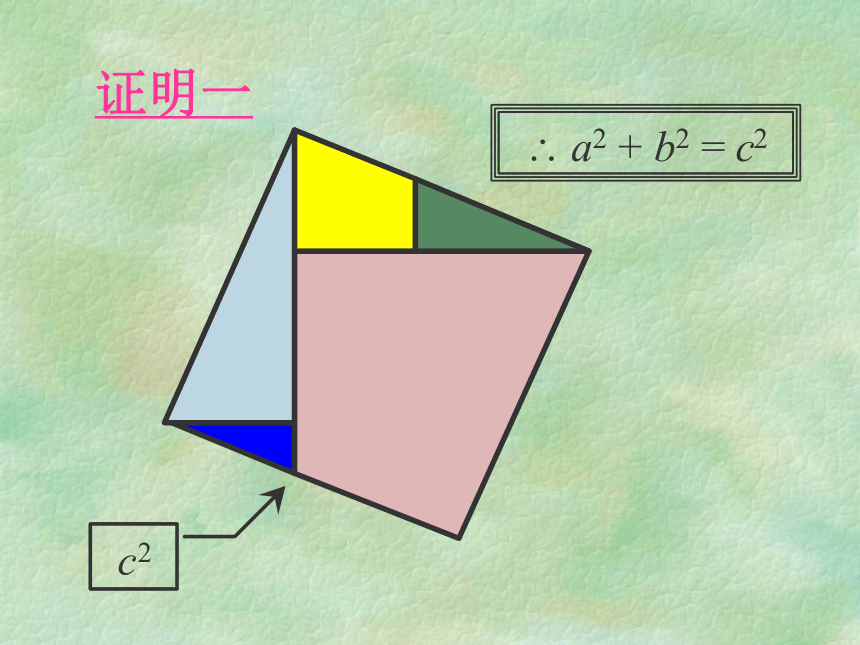
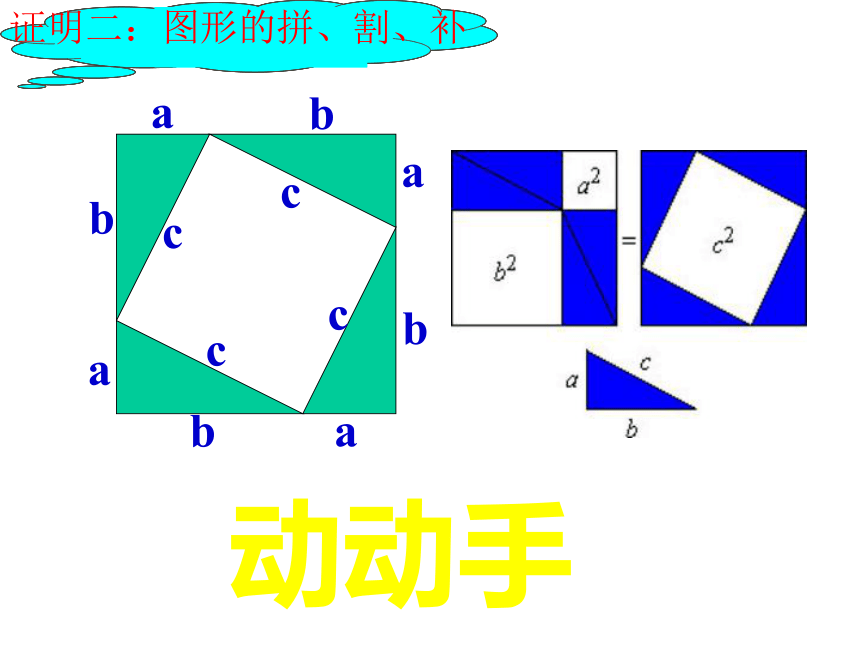
课件17张PPT。勾股定理 证明一证明二:图形的拼、割、补动动手
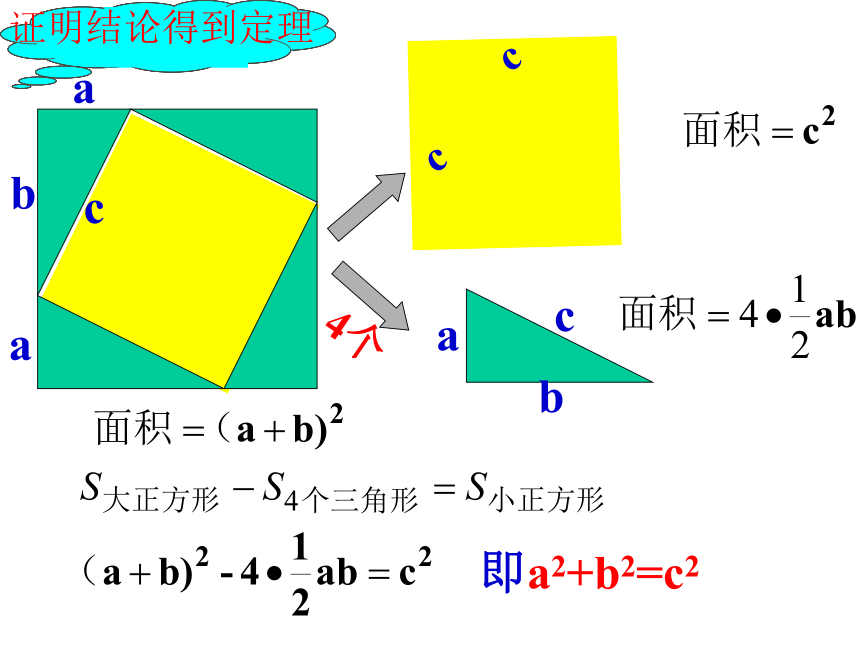
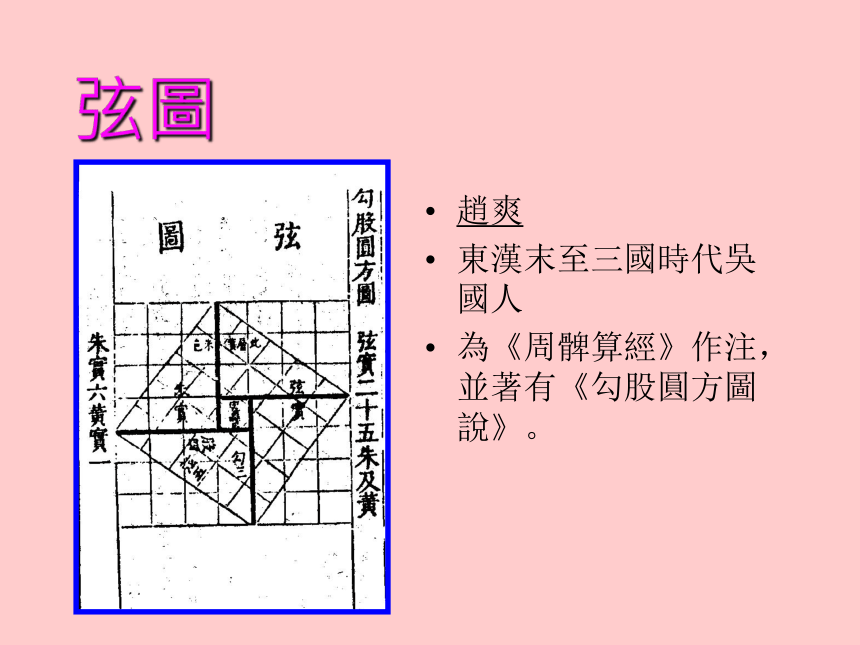
即a2+b2=c2证明结论得到定理弦圖趙爽
東漢末至三國時代吳國人
為《周髀算經》作注,並著有《勾股圓方圖說》。 公元三世纪,三国时代的东吴数学家赵爽用非常优美
的 方法-弦图证明了勾股定理,该图不仅代表了古代中国
曾经为世界数学的发展作出过重要贡献,同时该图也了数学的简洁之美,因此被二十四届(北京)国际数学大会组委会确定为大会的徽标。
美國總統的證明加菲(James A. Garfield; 1831 ? 1881)1881 年成為美國第 20 任總統
1876 年提出有關證明美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法证明三勾股定理的应用例1 我方侦察员小王在距离东西向公路
400米处侦察,发现一辆敌方汽车在公路
上疾驶。他赶紧拿出红外测距仪,测得
汽车与他相距400米,10秒后,汽车与他
相距500米,你能帮小王计算敌方汽车的
速度吗?出入相補劉徽(生於公元三世紀)三國魏晉時代人。
魏景元四年(即 263 年)為古籍《九章算術》作注釋。
在注作中,提出以「出入相補」的原理來證明「勾股定理」。後人稱該圖為「青朱入出圖」。
青朱出入图幾何原本歐幾里得(Euclid of Alexandria; 約 325 B.C. ? 約 265 B.C.)歐幾里得的《幾何原本》是用公理方法建立演繹數學體系的最早典範。
「證明一」就是取材自《幾何原本》第一卷的第 47 命題。無字證明sin(a + b) = sin a cos b + sin b cos a印度婆什迦羅的證明? c2 = b2 + a2作业:P11习题1.2 1,2随堂练习
P10 1
即a2+b2=c2证明结论得到定理弦圖趙爽
東漢末至三國時代吳國人
為《周髀算經》作注,並著有《勾股圓方圖說》。 公元三世纪,三国时代的东吴数学家赵爽用非常优美
的 方法-弦图证明了勾股定理,该图不仅代表了古代中国
曾经为世界数学的发展作出过重要贡献,同时该图也了数学的简洁之美,因此被二十四届(北京)国际数学大会组委会确定为大会的徽标。
美國總統的證明加菲(James A. Garfield; 1831 ? 1881)1881 年成為美國第 20 任總統
1876 年提出有關證明美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法证明三勾股定理的应用例1 我方侦察员小王在距离东西向公路
400米处侦察,发现一辆敌方汽车在公路
上疾驶。他赶紧拿出红外测距仪,测得
汽车与他相距400米,10秒后,汽车与他
相距500米,你能帮小王计算敌方汽车的
速度吗?出入相補劉徽(生於公元三世紀)三國魏晉時代人。
魏景元四年(即 263 年)為古籍《九章算術》作注釋。
在注作中,提出以「出入相補」的原理來證明「勾股定理」。後人稱該圖為「青朱入出圖」。
青朱出入图幾何原本歐幾里得(Euclid of Alexandria; 約 325 B.C. ? 約 265 B.C.)歐幾里得的《幾何原本》是用公理方法建立演繹數學體系的最早典範。
「證明一」就是取材自《幾何原本》第一卷的第 47 命題。無字證明sin(a + b) = sin a cos b + sin b cos a印度婆什迦羅的證明? c2 = b2 + a2作业:P11习题1.2 1,2随堂练习
P10 1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
