浙江省温州市瓯海区三溪中学高中数学人教版必修一3-1-2用二分法求方程的近似解课件(共14张PPT)
文档属性
| 名称 | 浙江省温州市瓯海区三溪中学高中数学人教版必修一3-1-2用二分法求方程的近似解课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 71.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-24 09:49:49 | ||
图片预览






文档简介
课件14张PPT。 用二分法求方程的近似解复习思考:1.函数的零点2.零点存在的判定3.零点个数的求法 使f(x)=0的实数x叫做函数y=f(x)的零点 ①代数法 ②图像法有12个球,其中有一个比别的球重,你用天平称几次可以找出这个球?次数越少越好 ?第一次,两端各放6个,低的那端有重球.
第二次,两端各放3个,低的那端有重球.
第三次,两端各放1个,如果平了,剩下的那个就是,否则低的那端那个就是!问题1:CCTV2“幸运52”片段 :
主持人李咏说道:猜一猜这架家用型数码相机的价格.观众甲:2000!李咏:高了! 观众乙:1000! 李咏:低了! 观众丙:1500! 李咏:还是低了!·······
问题1:你知道这件商品的价格在什么范围内吗?
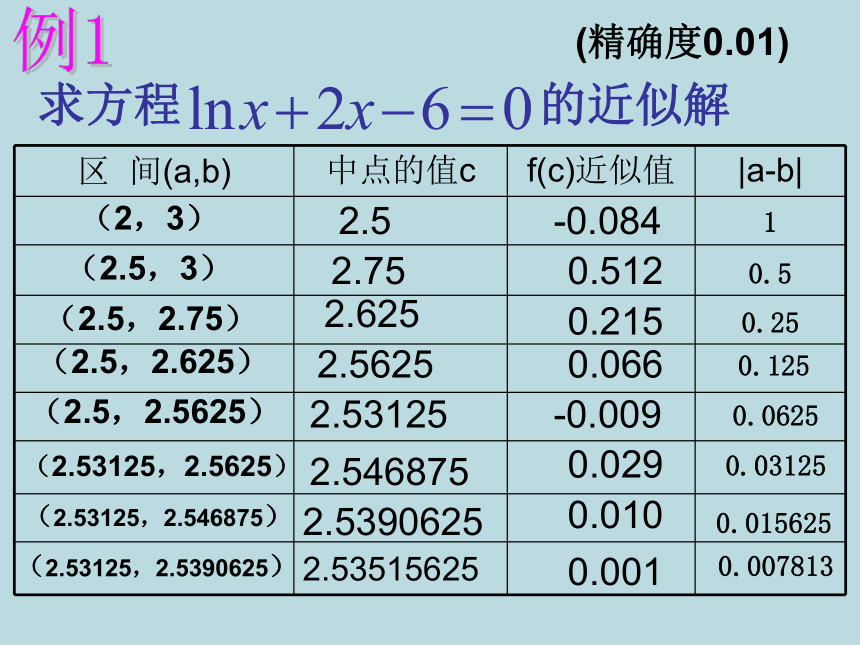
问题2:若接下来让你猜的话,你会猜多少价格比较合理呢?答案:1500至2000之间问题2:f(2)·f(3)<02.52.752.6252.56252.531252.5468752.53906252.53515625-0.0840.5120.2150.066-0.0090.029 0.0100.001(精确度0.01)(2,3)求方程的近似解
(2.5,3)(2.5,2.75)(2.5,2.625)(2.5,2.5625)(2.53125,2.5625) (2.53125,2.546875) (2.53125,2.5390625)例110.50.250.1250.06250.031250.0156250.007813二分法:对于在区间[a,b]上连续不断且f(a) f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。一、定义思考1:求函数f(x)的零点近似值第一步应做什么? 思考2:为了缩小零点所在区间的范围,接下来应做什么? 确定区间[a,b],使 f(a)f(b)<0 求区间的中点c,并计算f(c)的值 思考3:若f(c)=0说明什么?
若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么? 若f(c)=0 ,则c就是函数的零点; 若f(a)·f(c)<0 ,则零点x0∈(a,c);若f(c)·f(b)<0 ,则零点x0∈(c,b).思考4:若给定精确度ε,如何选取近似值? 当|a—b|<ε时,区间[a,b]内的任意一个值都是函数零点的近似值. 二、给定精确度 ,用二分法求函数f(x)零点近似值的步骤如下:1、确定区间[a,b],验证f(a) f(b)<0,给定精确度 ;
2、求区间(a,b)的中点c;
3、计算 f(c);
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a) f(c)<0,则令b=c(此时零点 );
(3)若f(c) f(b)<0,则令a=c(此时零点 )。
4、判断是否达到精确度 :即若 ,
则得到零点近似值a(或b);否则重复2~4。借助计算器或计算机用二分法求方程
的近似解(精确度为0.1)-6-2310214075142273例2 因为 f(1)·f(2)<0 所以 f(x)= 2x+3x-7在
(1,2)内有零点x0,取(1,2)的中点 x1=1.5, f(1.5)= 0.33,
因为f(1)·f(1.5)<0所以x0 ∈(1,1.5)
取(1,1.5)的中点x2=1.25 ,f(1.25)= -0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5)同理可得, x0∈(1.375,1.5),
x0∈(1.375,1.4375),由于
|1.375-1.4375|=0.0625<0.1
所以,原方程的近似解可取为1.4375课堂小结1、二分法定义
2、给定精确度 ,用二分法求函数f(x)零点近似值的步骤.再 见!
第二次,两端各放3个,低的那端有重球.
第三次,两端各放1个,如果平了,剩下的那个就是,否则低的那端那个就是!问题1:CCTV2“幸运52”片段 :
主持人李咏说道:猜一猜这架家用型数码相机的价格.观众甲:2000!李咏:高了! 观众乙:1000! 李咏:低了! 观众丙:1500! 李咏:还是低了!·······
问题1:你知道这件商品的价格在什么范围内吗?
问题2:若接下来让你猜的话,你会猜多少价格比较合理呢?答案:1500至2000之间问题2:f(2)·f(3)<02.52.752.6252.56252.531252.5468752.53906252.53515625-0.0840.5120.2150.066-0.0090.029 0.0100.001(精确度0.01)(2,3)求方程的近似解
(2.5,3)(2.5,2.75)(2.5,2.625)(2.5,2.5625)(2.53125,2.5625) (2.53125,2.546875) (2.53125,2.5390625)例110.50.250.1250.06250.031250.0156250.007813二分法:对于在区间[a,b]上连续不断且f(a) f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。一、定义思考1:求函数f(x)的零点近似值第一步应做什么? 思考2:为了缩小零点所在区间的范围,接下来应做什么? 确定区间[a,b],使 f(a)f(b)<0 求区间的中点c,并计算f(c)的值 思考3:若f(c)=0说明什么?
若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么? 若f(c)=0 ,则c就是函数的零点; 若f(a)·f(c)<0 ,则零点x0∈(a,c);若f(c)·f(b)<0 ,则零点x0∈(c,b).思考4:若给定精确度ε,如何选取近似值? 当|a—b|<ε时,区间[a,b]内的任意一个值都是函数零点的近似值. 二、给定精确度 ,用二分法求函数f(x)零点近似值的步骤如下:1、确定区间[a,b],验证f(a) f(b)<0,给定精确度 ;
2、求区间(a,b)的中点c;
3、计算 f(c);
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a) f(c)<0,则令b=c(此时零点 );
(3)若f(c) f(b)<0,则令a=c(此时零点 )。
4、判断是否达到精确度 :即若 ,
则得到零点近似值a(或b);否则重复2~4。借助计算器或计算机用二分法求方程
的近似解(精确度为0.1)-6-2310214075142273例2 因为 f(1)·f(2)<0 所以 f(x)= 2x+3x-7在
(1,2)内有零点x0,取(1,2)的中点 x1=1.5, f(1.5)= 0.33,
因为f(1)·f(1.5)<0所以x0 ∈(1,1.5)
取(1,1.5)的中点x2=1.25 ,f(1.25)= -0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5)同理可得, x0∈(1.375,1.5),
x0∈(1.375,1.4375),由于
|1.375-1.4375|=0.0625<0.1
所以,原方程的近似解可取为1.4375课堂小结1、二分法定义
2、给定精确度 ,用二分法求函数f(x)零点近似值的步骤.再 见!
