八年级数学下册(北师大版)课件:2.2不等式的基本性质(共25张PPT)
文档属性
| 名称 | 八年级数学下册(北师大版)课件:2.2不等式的基本性质(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 492.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-23 00:00:00 | ||
图片预览






文档简介
课件25张PPT。2.2 不等式的基本性质
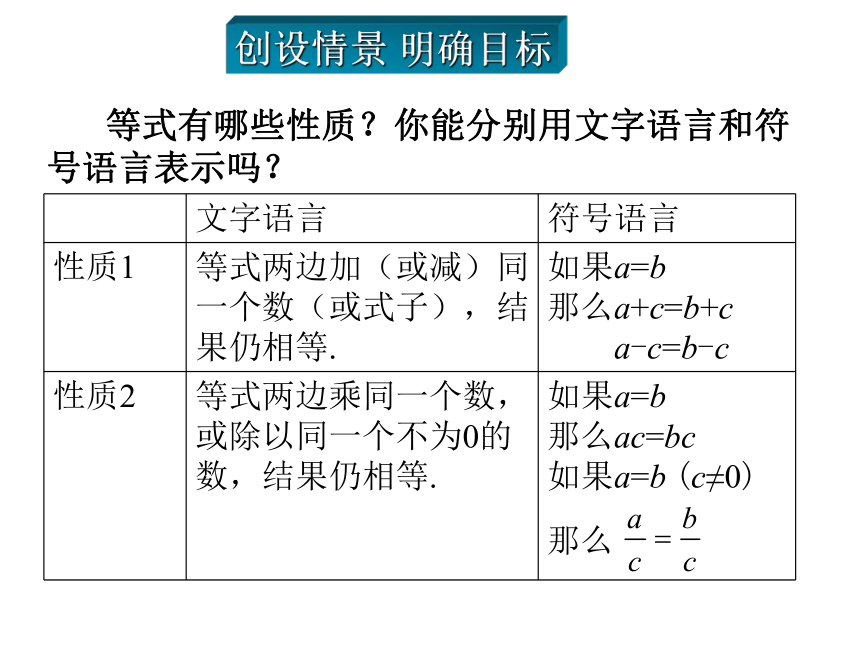
等式有哪些性质?你能分别用文字语言和符号语言表示吗?创设情景 明确目标某地庆典活动需燃放某种礼花弹.为确保人身安全,要求燃放者在点燃导火索后于燃放前转移到10米以外的地方.已知导火索的燃烧速度为0.02 m/s,人离开的速度是4 m/s,导火索的长x(m)应满足怎样的关系式?你会解这个不等式吗?1.探索并理解不等式的性质.
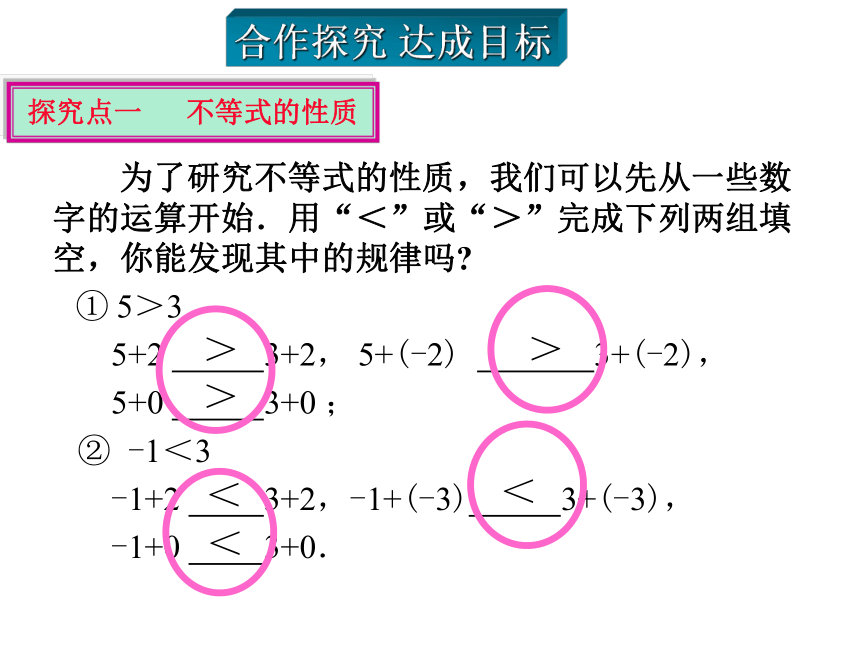
2.体会探索过程中所应用的归纳和类比的方法.学习目标 为了研究不等式的性质,我们可以先从一些数字的运算开始.用“<”或“>”完成下列两组填空,你能发现其中的规律吗?
① 5>3
5+2 3+2, 5+(-2) 3+(-2),
5+0 3+0 ;
② -1<3
-1+2 3+2,-1+(-3) 3+(-3),
-1+0 3+0.>>><<<合作探究 达成目标探究点一 不等式的性质观察不等号的变化,发现并归纳其中的规律,
获得以下猜想.猜想1 当不等式两边加(或减)同一个数
(或式子)时,不等号的方向不变.追问 猜想1是否正确?如何验证? 性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变. 类似等式性质的符号语言表示,你能把不等式的性质1用符号语言表示吗?用“<”或“>”填空,并总结其中的规律:
① 6>2,
6×5 ___2×5,
6×(-5)___ 2 ×(-5);
② -2<3 ,
(-2)×6___ 3×6,
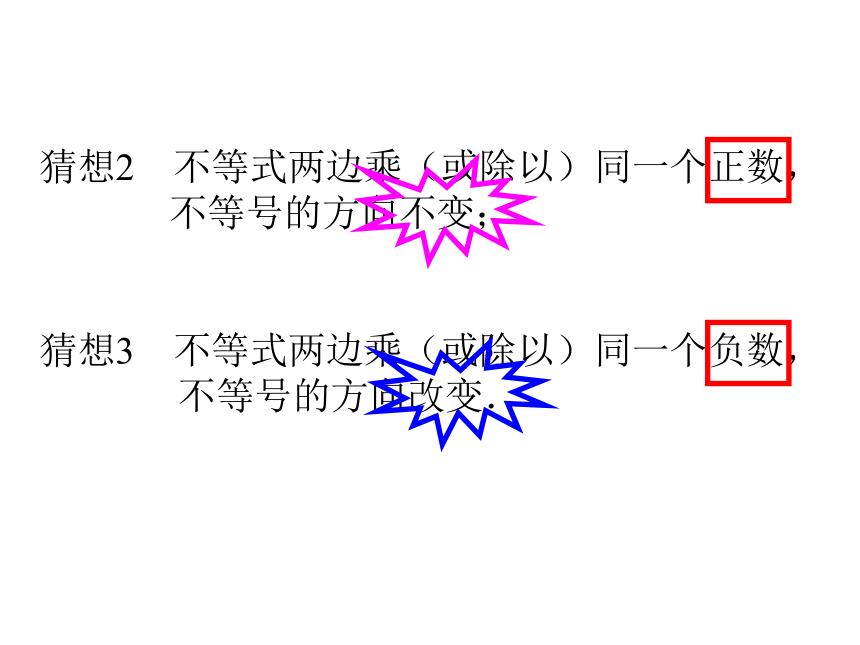
(-2)×(-6)___ 3 ×(-6).<>><猜想2 不等式两边乘(或除以)同一个正数,
不等号的方向不变;
猜想3 不等式两边乘(或除以)同一个负数,
不等号的方向改变. 性质2:不等式两边乘(或除以)同一个正数,
不等号的方向不变.
性质3:不等式两边乘(或除以)同一个负数,
不等号的方向改变. 探究点二 利用不等式的性质解不等式例1 利用不等式的性质解下列不等式:
(1) ; (2) ;
(3) ; (4) .(1) ; 分析:解未知数为x的不等式,就是要使不等式逐步化为 或 的形式.
解:根据不等式的性质1,
不等式两边都加7,不等号的方向不变,
得
(2) ; 解:根据不等式的性质1,
不等式两边都减 ,不等号的方向不变,
得
(3) ; 解:根据不等式的性质2,
不等式两边都乘以 ,不等号的方向不变,
得
(4) ; 解:根据不等式的性质3,
不等式两边都乘以 ,不等号的方向改变,
得
请将例1中四个小题的解集用数轴表示出来:(1) ; (2) ;请将例1中四个小题的解集用数轴表示出来:(3) ; (4) .0750将不等式逐步转化为 或 ( 为常数)的形式的依据是不等式的性质.不等式的两边同乘或除同一个数时,要分清乘或除的是正数还是负数,若是正数不等号的方向不变,若是负数不等号方向要改变.把不等式逐步转化为 或 ( 为常数)的形式的依据是什么?应注意什么问题?探究点二 利用不等式的性质解不等式例2 某长方体形状的容器长5 cm,宽3cm,高10cm,容器内原有水的高度为3 cm,现准备向它继续注水。用V(单位:cm3)表示新注入水的体积,写出V的取值范围。
探究点三 不等式性质的实际运用分析:“不超过” 是什么意思?体积应满足怎样的关系式?新注入水的体积 能是负数吗?在表示0和105的点上画实心圆点,表示取值范围包括这两个数.V ≤1050≤ V ≤105在数轴上表示例2的解集与表示例1的解集有什么不同?探究点三 不等式性质的实际运用在数轴上表示不等式例1的解集不具有实际意义,因此不用考虑它的是否符合生活实际;而例2中未知数是具有实际意义,因此必须考虑它符合生活实际,且例2的解集用到的是“≤”、“≥”,它表示小于或等于、大于或等于,表示包含这个数,因此用实心点表示.总结梳理 内化目标达标检测 反思目标
1.上交作业:教材习题;
等式有哪些性质?你能分别用文字语言和符号语言表示吗?创设情景 明确目标某地庆典活动需燃放某种礼花弹.为确保人身安全,要求燃放者在点燃导火索后于燃放前转移到10米以外的地方.已知导火索的燃烧速度为0.02 m/s,人离开的速度是4 m/s,导火索的长x(m)应满足怎样的关系式?你会解这个不等式吗?1.探索并理解不等式的性质.
2.体会探索过程中所应用的归纳和类比的方法.学习目标 为了研究不等式的性质,我们可以先从一些数字的运算开始.用“<”或“>”完成下列两组填空,你能发现其中的规律吗?
① 5>3
5+2 3+2, 5+(-2) 3+(-2),
5+0 3+0 ;
② -1<3
-1+2 3+2,-1+(-3) 3+(-3),
-1+0 3+0.>>><<<合作探究 达成目标探究点一 不等式的性质观察不等号的变化,发现并归纳其中的规律,
获得以下猜想.猜想1 当不等式两边加(或减)同一个数
(或式子)时,不等号的方向不变.追问 猜想1是否正确?如何验证? 性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变. 类似等式性质的符号语言表示,你能把不等式的性质1用符号语言表示吗?用“<”或“>”填空,并总结其中的规律:
① 6>2,
6×5 ___2×5,
6×(-5)___ 2 ×(-5);
② -2<3 ,
(-2)×6___ 3×6,
(-2)×(-6)___ 3 ×(-6).<>><猜想2 不等式两边乘(或除以)同一个正数,
不等号的方向不变;
猜想3 不等式两边乘(或除以)同一个负数,
不等号的方向改变. 性质2:不等式两边乘(或除以)同一个正数,
不等号的方向不变.
性质3:不等式两边乘(或除以)同一个负数,
不等号的方向改变. 探究点二 利用不等式的性质解不等式例1 利用不等式的性质解下列不等式:
(1) ; (2) ;
(3) ; (4) .(1) ; 分析:解未知数为x的不等式,就是要使不等式逐步化为 或 的形式.
解:根据不等式的性质1,
不等式两边都加7,不等号的方向不变,
得
(2) ; 解:根据不等式的性质1,
不等式两边都减 ,不等号的方向不变,
得
(3) ; 解:根据不等式的性质2,
不等式两边都乘以 ,不等号的方向不变,
得
(4) ; 解:根据不等式的性质3,
不等式两边都乘以 ,不等号的方向改变,
得
请将例1中四个小题的解集用数轴表示出来:(1) ; (2) ;请将例1中四个小题的解集用数轴表示出来:(3) ; (4) .0750将不等式逐步转化为 或 ( 为常数)的形式的依据是不等式的性质.不等式的两边同乘或除同一个数时,要分清乘或除的是正数还是负数,若是正数不等号的方向不变,若是负数不等号方向要改变.把不等式逐步转化为 或 ( 为常数)的形式的依据是什么?应注意什么问题?探究点二 利用不等式的性质解不等式例2 某长方体形状的容器长5 cm,宽3cm,高10cm,容器内原有水的高度为3 cm,现准备向它继续注水。用V(单位:cm3)表示新注入水的体积,写出V的取值范围。
探究点三 不等式性质的实际运用分析:“不超过” 是什么意思?体积应满足怎样的关系式?新注入水的体积 能是负数吗?在表示0和105的点上画实心圆点,表示取值范围包括这两个数.V ≤1050≤ V ≤105在数轴上表示例2的解集与表示例1的解集有什么不同?探究点三 不等式性质的实际运用在数轴上表示不等式例1的解集不具有实际意义,因此不用考虑它的是否符合生活实际;而例2中未知数是具有实际意义,因此必须考虑它符合生活实际,且例2的解集用到的是“≤”、“≥”,它表示小于或等于、大于或等于,表示包含这个数,因此用实心点表示.总结梳理 内化目标达标检测 反思目标
1.上交作业:教材习题;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
