华师大版数学七年级下册9.3用正多边形铺设地面课件(共20张PPT)
文档属性
| 名称 | 华师大版数学七年级下册9.3用正多边形铺设地面课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-23 10:49:33 | ||
图片预览




文档简介
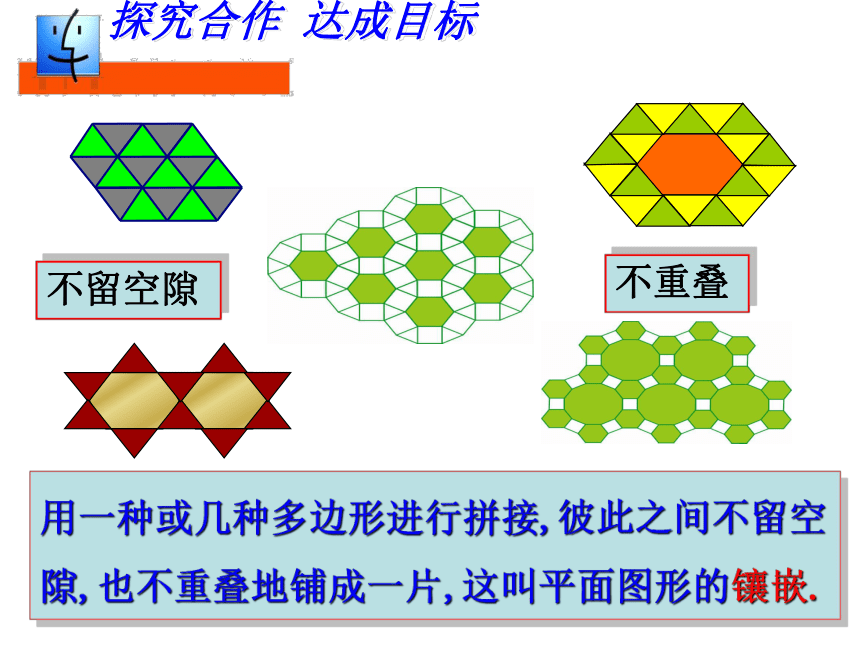
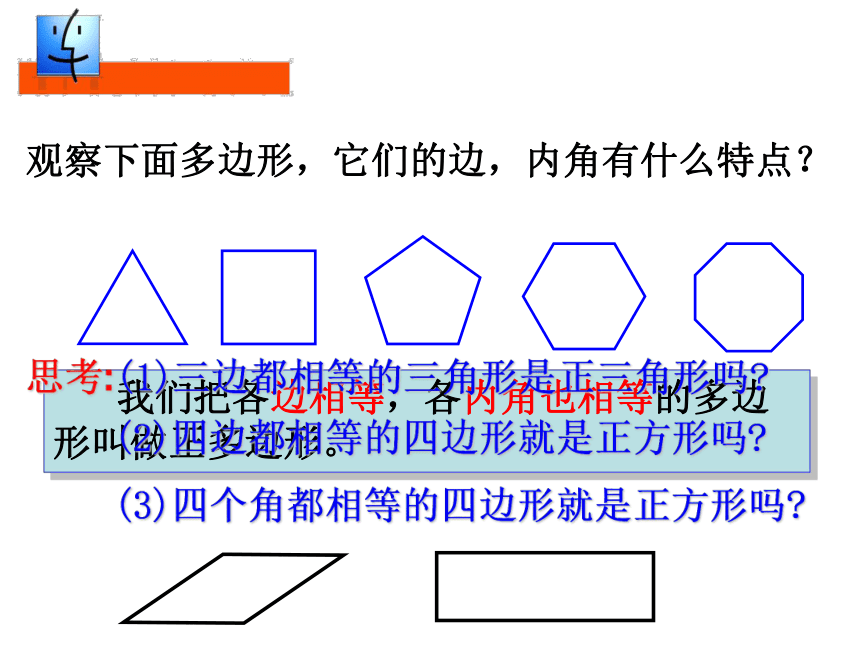
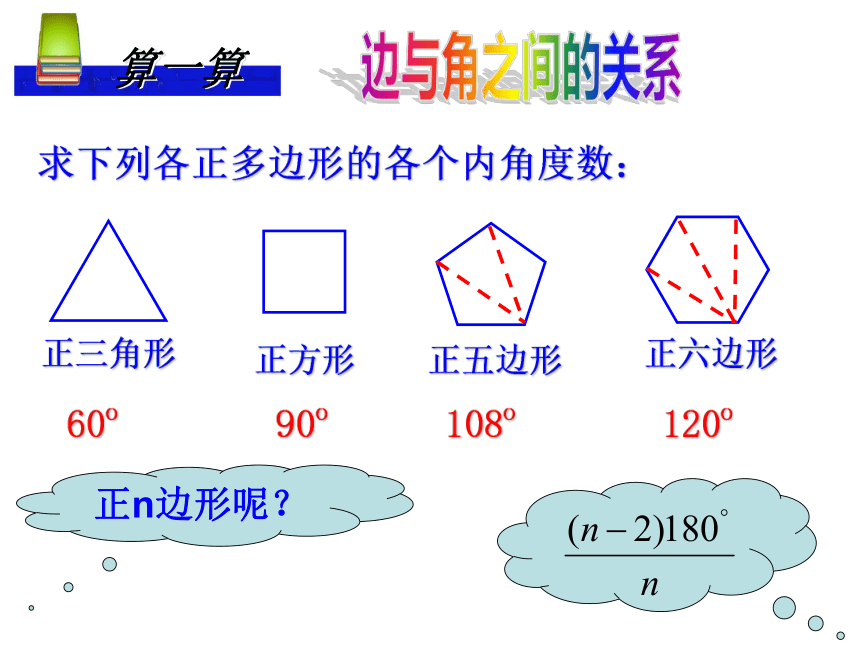
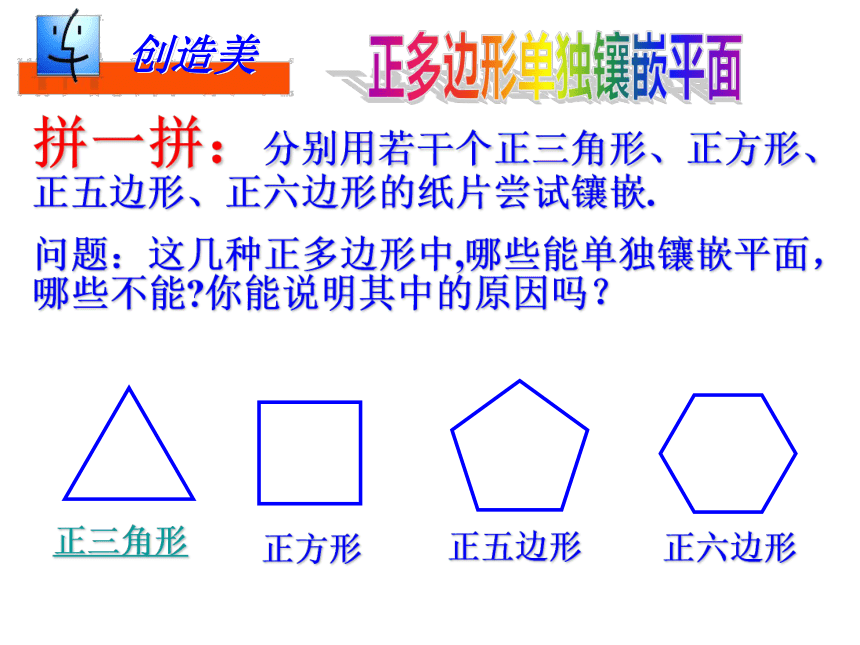
课件20张PPT。 9.3 用正多边形铺设地面有钱人与瓷砖店老板的故事创设情景 明确目标不留空隙不重叠探究合作 达成目标 用一种或几种多边形进行拼接,彼此之间不留空隙,也不重叠地铺成一片,这叫平面图形的镶嵌.观察下面多边形,它们的边,内角有什么特点? 我们把各边相等,各内角也相等的多边形叫做正多边形。(2)四边都相等的四边形就是正方形吗?(3)四个角都相等的四边形就是正方形吗?思考:(1)三边都相等的三角形是正三角形吗?求下列各正多边形的各个内角度数:60o90o108o120o正n边形呢? 算一算边与角之间的关系拼一拼:分别用若干个正三角形、正方形、正五边形、正六边形的纸片尝试镶嵌.
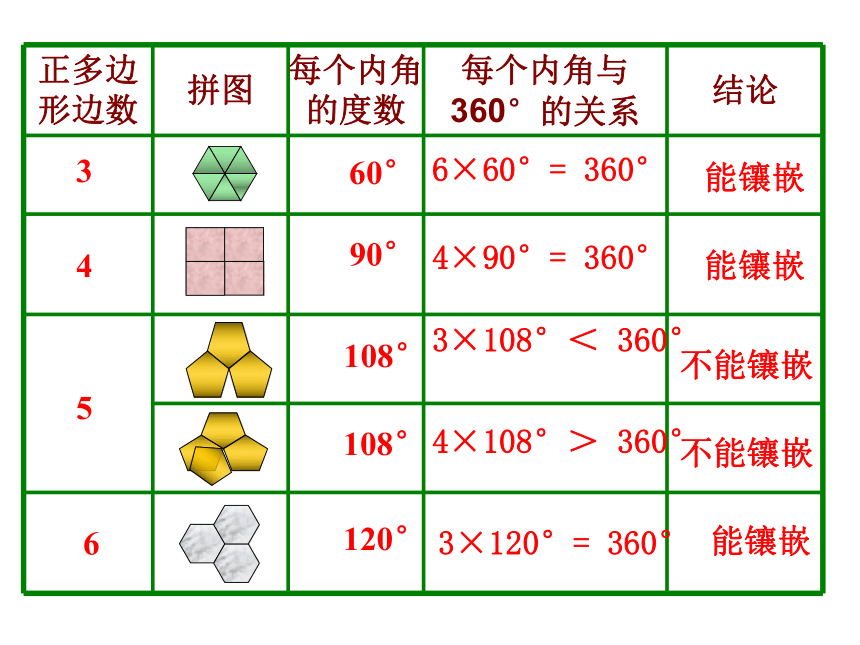
问题:这几种正多边形中,哪些能单独镶嵌平面,哪些不能?你能说明其中的原因吗?创造美正多边形单独镶嵌平面能镶嵌能镶嵌不能镶嵌不能镶嵌能镶嵌60°90°108°108°120°36456×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°规律小结: (1)如果正多边形能够镶嵌平面,那么共顶点的各个角的度数之和应等于360°.
(2)能单独用来镶嵌平面的正多边形的内角度数一定能整除360.总结梳理 内化目标能用下列正多边形单独镶嵌平面吗?结论:能单独镶嵌平面的正多边形只有3种,即正三角形、正方形、正六边形。试一试(1)正八边形;
(2)正十边形;
(3)正二十边形;用边长相等的正八边形和正方形能镶嵌平面吗?解:因为正八边形的内角为135o,正方形的内角为90o,由于135o×2+90o×1=360o,所以两个正八边形和一个正方形能拼成一幅镶嵌图。例题如果有钱人想用正三角形、正四边形、正六边形中的两种来镶嵌地面,他该如何选择材料?达标检测 反思目标3×60° + 2 ×90°= 360° 2×60°+2 ×120°=360°4×60°+1 ×120°=360°正三角形正四边形正三角形正六边形解:设共顶点的正三角形有x个,正六边形有y个,由题意得
60° x + 120°y= 360° x = 6 - 2y 当y=1时,x=4
当y=2时,x=2创造美选择边长相等的正多边形中的两种或两种以上进行镶嵌平面,使拼出的图案既符合要求又比较美观,比一比,哪一组同学最快展示作品?并说明其中的数学原理。 多种正多边形镶嵌平面探究:全等的三角形、全等的四边形能单独镶嵌平面吗?①②拓展任意相同多边形单独镶嵌平面形状、大小完全相同的任意三角形可以镶嵌平面.共顶点的各个角的度数之和等于360°拓展任意相同多边形单独镶嵌平面形状、大小完全相同的任意四边形可以镶嵌平面。共顶点的各个角的度数之和等于360°拓展任意相同多边形单独镶嵌平面拓展任意相同多边形单独镶嵌平面教材习题 课后作业
问题:这几种正多边形中,哪些能单独镶嵌平面,哪些不能?你能说明其中的原因吗?创造美正多边形单独镶嵌平面能镶嵌能镶嵌不能镶嵌不能镶嵌能镶嵌60°90°108°108°120°36456×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°规律小结: (1)如果正多边形能够镶嵌平面,那么共顶点的各个角的度数之和应等于360°.
(2)能单独用来镶嵌平面的正多边形的内角度数一定能整除360.总结梳理 内化目标能用下列正多边形单独镶嵌平面吗?结论:能单独镶嵌平面的正多边形只有3种,即正三角形、正方形、正六边形。试一试(1)正八边形;
(2)正十边形;
(3)正二十边形;用边长相等的正八边形和正方形能镶嵌平面吗?解:因为正八边形的内角为135o,正方形的内角为90o,由于135o×2+90o×1=360o,所以两个正八边形和一个正方形能拼成一幅镶嵌图。例题如果有钱人想用正三角形、正四边形、正六边形中的两种来镶嵌地面,他该如何选择材料?达标检测 反思目标3×60° + 2 ×90°= 360° 2×60°+2 ×120°=360°4×60°+1 ×120°=360°正三角形正四边形正三角形正六边形解:设共顶点的正三角形有x个,正六边形有y个,由题意得
60° x + 120°y= 360° x = 6 - 2y 当y=1时,x=4
当y=2时,x=2创造美选择边长相等的正多边形中的两种或两种以上进行镶嵌平面,使拼出的图案既符合要求又比较美观,比一比,哪一组同学最快展示作品?并说明其中的数学原理。 多种正多边形镶嵌平面探究:全等的三角形、全等的四边形能单独镶嵌平面吗?①②拓展任意相同多边形单独镶嵌平面形状、大小完全相同的任意三角形可以镶嵌平面.共顶点的各个角的度数之和等于360°拓展任意相同多边形单独镶嵌平面形状、大小完全相同的任意四边形可以镶嵌平面。共顶点的各个角的度数之和等于360°拓展任意相同多边形单独镶嵌平面拓展任意相同多边形单独镶嵌平面教材习题 课后作业
