重庆市长寿区七校联盟2023-2024学年高一下学期7月期末检测(B)数学试题(含答案)
文档属性
| 名称 | 重庆市长寿区七校联盟2023-2024学年高一下学期7月期末检测(B)数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 972.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 23:43:51 | ||
图片预览



文档简介
长寿区七校联盟2023-2024学年高一下学期7月期末检测(B)
数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数满足,则复数的虚部为( )
A. B. C. D.
2.已知向量,满足,且,则与的夹角为( )
A. B. C. D.
3.已知向量,,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.在中, 、 、 分别是内角 、 、 所对的边,若,,,则边 ( )
A. B. 或 C. 或 D.
5.科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号如图是中国科学院空天信息研究院自主研发的系留浮空器,年月,“极目一号”Ⅲ型浮空艇成功完成次升空大气科学观测,最高升空至米,超过珠穆朗玛峰,创造了浮空艇大气科学观测海拔最高的世界纪录,彰显了中国的实力,“极目一号”Ⅲ型浮空艇长米,高米,若将它近似看作一个半球,一个圆柱和一个圆台的组合体,轴截面图如图所示,则“极目一号”Ⅲ型浮空艇的体积约为( )
A. B. C. D.
6.如图,在长方体中,若,,,分别是棱,,,的中点,则下列结论一定成立的是( )
A. 四边形是矩形 B. 四边形是正方形
C. D. 平面平面
7.有一个样本量为的数据分组,各组的频数如下:
分组
频数
根据频数分布,估计小于的数据大约占总体的( )
A. B. C. D.
8.一个电路如图所示,为个开关,其闭合的概率均为,且是相互独立的,则灯亮的概率是( )
A. B. C. D.
二、多选题:本题共3小题,每题6分,共16分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在菱形中,,延长边至点,使得动点从点出发,沿菱形的边按逆时针方向运动一周回到点,若,则( )
A. 满足的点有且只有一个 B. 满足的点有两个
C. 存在最小值 D. 不存在最大值
10.如图,为圆锥底面圆的直径,点是圆上异于,的动点,,则下列结论正确的是( )
A. 圆锥 的侧面积为
B. 三棱锥体积的最大值为
C. 的取值范围是
D. 若,为线段上的动点,则的最小值为
11.一工厂将两盒产品送检,甲盒中有个一等品,个二等品和个三等品,乙盒中有个一等品,个二等品和个三等品.先从甲盒中随机取出一个产品放入乙盒,分别以,和表示由甲盒取出的产品是一等品,二等品和三等品的事件;再从乙盒中随机取出一产品,以表示由乙盒取出的产品是一等品的事件.则下列结论中正确的是( )
A. ; B. ;
C. 事件与事件相互独立; D. ,,是两两互斥的事件.
三、填空题:本题共3小题,每小题5分,共15分。
12.设复数,,满足,,则 .
13.若一组数据,,,的方差是,则数据,,,的方差是 .
14.已知平面向量,,满足,,,且,则的最大值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题13分在中国共产主义青年团成立周年之际,某校举办了“强国有我,挑战答题”的知识竞赛活动,已知甲、乙两队参加,每队人,每人回答且仅回答一个问题,答对者为本队赢得分,答错得分.假设甲队中人答对的概率分别为,,,乙队中每人答对的概率均为,且各人回答问题正确与否互不影响.
分别求甲队总得分为分和分的概率;
求活动结束后,甲、乙两队共得分的概率.
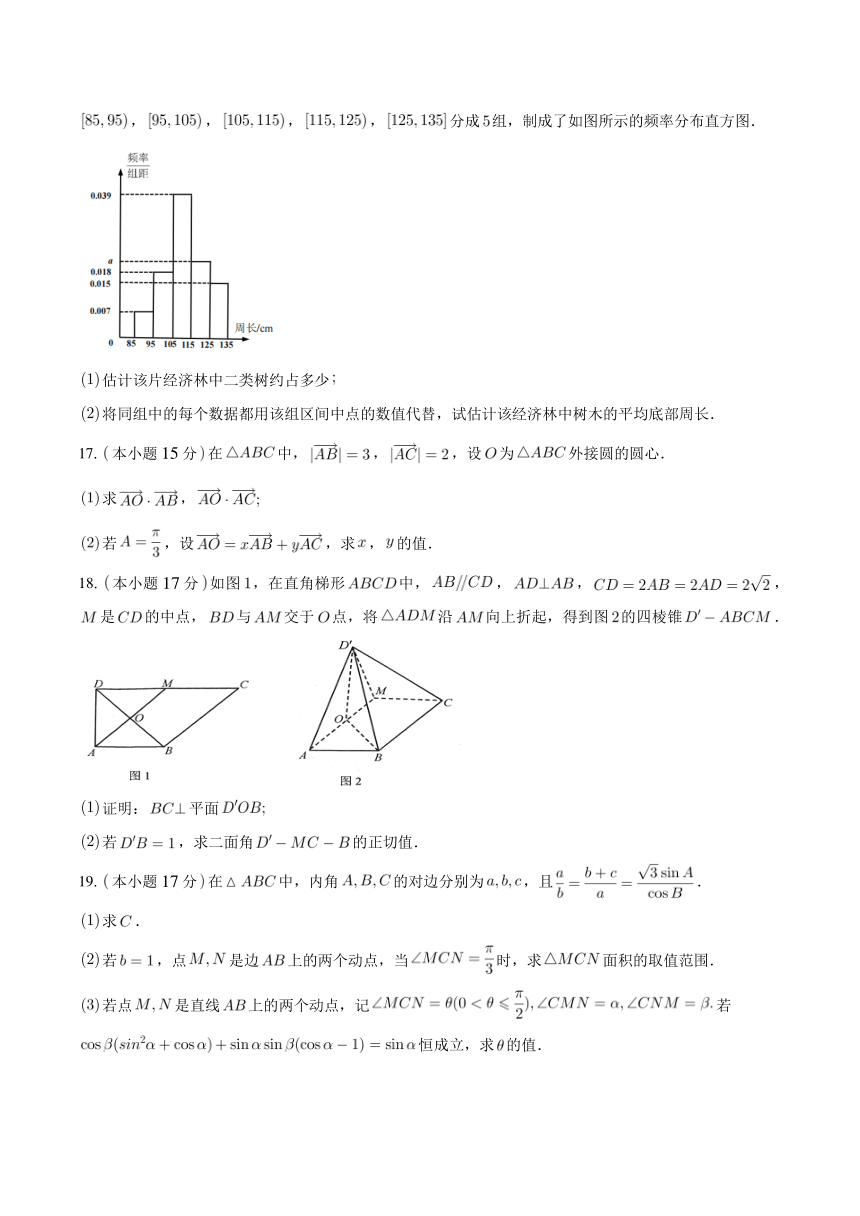
16.本小题15分某种经济树木根据其底部周长的不同售价有所差异,底部周长在为三类树,底部周长在为二类树,底部周长大于或等于为一类树为了解一大片该经济林的生长情况,随机测量其中株树木的底部周长单位:,数据均落在之间,按照,,,,分成组,制成了如图所示的频率分布直方图.
估计该片经济林中二类树约占多少
将同组中的每个数据都用该组区间中点的数值代替,试估计该经济林中树木的平均底部周长.
17.本小题15分在中,,,设为外接圆的圆心.
求,
若,设,求,的值.
18.本小题17分如图,在直角梯形中,,,,是的中点,与交于点,将沿向上折起,得到图的四棱锥.
证明:平面
若,求二面角的正切值.
19.本小题17分在中,内角的对边分别为,且.
求.
若,点是边上的两个动点,当时,求面积的取值范围.
若点是直线上的两个动点,记若恒成立,求的值.
数学参考答案
1-5.BCBCA 6-8.AAC
9. 10. 11.
12.; 13. ; 14.
15.解:设甲队总得分为分为事件,甲队总得分为分为事件,
则.
.
所以甲队总得分为分的概率为,分的概率为.
依题意甲队总得分为分,即道题全部错误的概率为
.
得分的概率为,得分的概率为,得分的概率为;
乙队总得分为分的概率为,得分的概率为,
得分的概率为,得分的概率为.
则活动结束后,甲、乙两队共得分的概率
.
16.解:由频率分布直方图可得,
,
所以,解得.
因为底部周长在为二类树,
所以由图可得,.
答:该片经济林中二类树木约占。
由题意可得,
答:估计该经济林中树木的平均底部周长为.
17.解:如图,由于为外接圆的圆心,所以.
设,的中点分别为,,连接,,则,.
故.
同理可得.
由可得
.
即解得,.
18.解:证明:在图中,连接,由已知得,,是的中点,
,,
四边形是平行四边形,,
同理可证四边形是平行四边形,,且,
四边形是正方形,,
在图中,,,
又,、平面,
平面,又,
平面.
,是等边三角形,
过作于点,则为中点,过作交延长线于点,连接.
平面,平面,
,又,,、平面,
平面,又平面,
,又,,、平面,
平面,平面,
,
即为二面角的平面角.
在等边中,,则,
在上图中,点为的中点,,,
可得,
在中,,
二面角的正切值为.
19.解:,由正弦定理得
,
因为,
所以,
因为,所以,
由,可得,即
,所以,
由正弦定理可得,
则,
得,
则或舍去,
所以;
因为,所以,,设,
当时,不存在即点与点重合,
此时,,,;
当时,不存在即点与点重合,
此时,为等边三角形,
;
当时,在中,由正弦定理得,
所以,
在中,由正弦定理得,
所以
,
的面积
,
因为,
所以,
则,
综上所述面积的取值范围为 ;
因为,
所以,
则,
即,
又是定值,所以是定值,
所以,因为为的内角,
所以,
故的值为.
数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数满足,则复数的虚部为( )
A. B. C. D.
2.已知向量,满足,且,则与的夹角为( )
A. B. C. D.
3.已知向量,,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.在中, 、 、 分别是内角 、 、 所对的边,若,,,则边 ( )
A. B. 或 C. 或 D.
5.科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号如图是中国科学院空天信息研究院自主研发的系留浮空器,年月,“极目一号”Ⅲ型浮空艇成功完成次升空大气科学观测,最高升空至米,超过珠穆朗玛峰,创造了浮空艇大气科学观测海拔最高的世界纪录,彰显了中国的实力,“极目一号”Ⅲ型浮空艇长米,高米,若将它近似看作一个半球,一个圆柱和一个圆台的组合体,轴截面图如图所示,则“极目一号”Ⅲ型浮空艇的体积约为( )
A. B. C. D.
6.如图,在长方体中,若,,,分别是棱,,,的中点,则下列结论一定成立的是( )
A. 四边形是矩形 B. 四边形是正方形
C. D. 平面平面
7.有一个样本量为的数据分组,各组的频数如下:
分组
频数
根据频数分布,估计小于的数据大约占总体的( )
A. B. C. D.
8.一个电路如图所示,为个开关,其闭合的概率均为,且是相互独立的,则灯亮的概率是( )
A. B. C. D.
二、多选题:本题共3小题,每题6分,共16分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在菱形中,,延长边至点,使得动点从点出发,沿菱形的边按逆时针方向运动一周回到点,若,则( )
A. 满足的点有且只有一个 B. 满足的点有两个
C. 存在最小值 D. 不存在最大值
10.如图,为圆锥底面圆的直径,点是圆上异于,的动点,,则下列结论正确的是( )
A. 圆锥 的侧面积为
B. 三棱锥体积的最大值为
C. 的取值范围是
D. 若,为线段上的动点,则的最小值为
11.一工厂将两盒产品送检,甲盒中有个一等品,个二等品和个三等品,乙盒中有个一等品,个二等品和个三等品.先从甲盒中随机取出一个产品放入乙盒,分别以,和表示由甲盒取出的产品是一等品,二等品和三等品的事件;再从乙盒中随机取出一产品,以表示由乙盒取出的产品是一等品的事件.则下列结论中正确的是( )
A. ; B. ;
C. 事件与事件相互独立; D. ,,是两两互斥的事件.
三、填空题:本题共3小题,每小题5分,共15分。
12.设复数,,满足,,则 .
13.若一组数据,,,的方差是,则数据,,,的方差是 .
14.已知平面向量,,满足,,,且,则的最大值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题13分在中国共产主义青年团成立周年之际,某校举办了“强国有我,挑战答题”的知识竞赛活动,已知甲、乙两队参加,每队人,每人回答且仅回答一个问题,答对者为本队赢得分,答错得分.假设甲队中人答对的概率分别为,,,乙队中每人答对的概率均为,且各人回答问题正确与否互不影响.
分别求甲队总得分为分和分的概率;
求活动结束后,甲、乙两队共得分的概率.
16.本小题15分某种经济树木根据其底部周长的不同售价有所差异,底部周长在为三类树,底部周长在为二类树,底部周长大于或等于为一类树为了解一大片该经济林的生长情况,随机测量其中株树木的底部周长单位:,数据均落在之间,按照,,,,分成组,制成了如图所示的频率分布直方图.
估计该片经济林中二类树约占多少
将同组中的每个数据都用该组区间中点的数值代替,试估计该经济林中树木的平均底部周长.
17.本小题15分在中,,,设为外接圆的圆心.
求,
若,设,求,的值.
18.本小题17分如图,在直角梯形中,,,,是的中点,与交于点,将沿向上折起,得到图的四棱锥.
证明:平面
若,求二面角的正切值.
19.本小题17分在中,内角的对边分别为,且.
求.
若,点是边上的两个动点,当时,求面积的取值范围.
若点是直线上的两个动点,记若恒成立,求的值.
数学参考答案
1-5.BCBCA 6-8.AAC
9. 10. 11.
12.; 13. ; 14.
15.解:设甲队总得分为分为事件,甲队总得分为分为事件,
则.
.
所以甲队总得分为分的概率为,分的概率为.
依题意甲队总得分为分,即道题全部错误的概率为
.
得分的概率为,得分的概率为,得分的概率为;
乙队总得分为分的概率为,得分的概率为,
得分的概率为,得分的概率为.
则活动结束后,甲、乙两队共得分的概率
.
16.解:由频率分布直方图可得,
,
所以,解得.
因为底部周长在为二类树,
所以由图可得,.
答:该片经济林中二类树木约占。
由题意可得,
答:估计该经济林中树木的平均底部周长为.
17.解:如图,由于为外接圆的圆心,所以.
设,的中点分别为,,连接,,则,.
故.
同理可得.
由可得
.
即解得,.
18.解:证明:在图中,连接,由已知得,,是的中点,
,,
四边形是平行四边形,,
同理可证四边形是平行四边形,,且,
四边形是正方形,,
在图中,,,
又,、平面,
平面,又,
平面.
,是等边三角形,
过作于点,则为中点,过作交延长线于点,连接.
平面,平面,
,又,,、平面,
平面,又平面,
,又,,、平面,
平面,平面,
,
即为二面角的平面角.
在等边中,,则,
在上图中,点为的中点,,,
可得,
在中,,
二面角的正切值为.
19.解:,由正弦定理得
,
因为,
所以,
因为,所以,
由,可得,即
,所以,
由正弦定理可得,
则,
得,
则或舍去,
所以;
因为,所以,,设,
当时,不存在即点与点重合,
此时,,,;
当时,不存在即点与点重合,
此时,为等边三角形,
;
当时,在中,由正弦定理得,
所以,
在中,由正弦定理得,
所以
,
的面积
,
因为,
所以,
则,
综上所述面积的取值范围为 ;
因为,
所以,
则,
即,
又是定值,所以是定值,
所以,因为为的内角,
所以,
故的值为.
同课章节目录
