广东省深圳市2023-2024学年南山区七年级下数学期末试卷(含手写答案)
文档属性
| 名称 | 广东省深圳市2023-2024学年南山区七年级下数学期末试卷(含手写答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 714.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 00:00:00 | ||
图片预览




文档简介
绝密★启用前 试卷类型: A
(
2024.07
)2023—2024学年第二学期期末教学质量监测 七年级数学试题
说明:1.答题前,请将学校、班级和姓名用规定的笔写在答题卷指定的位置上.
2.全卷分二部分,第一部分为选择题,第二部分为非选择题,共6页;考试时间90分钟,满分100
分 .
3. 本卷试题,考生必须在答题卡上作答;凡在试卷、草稿纸上作答的,其答案一律无效。答题 卡必须保持清洁,不能折叠.
4. 本卷选择题1~10,每小题选出答案后,用2B铅笔将答题卡选择题答题区内对应题目的答案标 号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案;非选择题11~22,答案(含作辅助
线)必须用规定的笔,按作答题目序号,写在答题卡非选择题答题区规定范围内. 5. 考试结束,请将答题卡交回.
第一部分选择题
一 、选择题(本题共有10小题,每小题3分,共30分.在每小题给出四个选项中,只有一项
是符合题目要求的,请将正确选项用2B铅笔填涂在答题卡上)
1. 我国新能源汽车发展势头迅猛,以下汽车车标融入了数学几何元素,其中是轴对称图形的是(▲)
A.
B.
C.
D.
2.红细胞是血液中数量最多的一种血细胞,它将氧气从肺送到身体各个组织,它的直径约为0.0000078m,
将0.0000078用科学记数法表示为(▲)
A.78×10·7 B.7.8×10·7 C.7.8×10·6 D.0.78×10·6
3. 下列计算正确的是(▲)
A.-m·(-m) =-m B.x ÷x =x4 C.(3x) =6x D.(-a ) =a
4.下列事件中,属于必然事件的是(▲)
A. 任意购买一张电影票,座位号是偶数
B. 梦到醒来会下雨,醒来后发现窗外在下雨
C. 解锁手机,提示微信收到了新消息
D. 随意掷一枚质地均匀的骰子,掷出的点数不超过6
2023-2024学年第二学期期末教学质量监测七年级数学第1页(共6页)
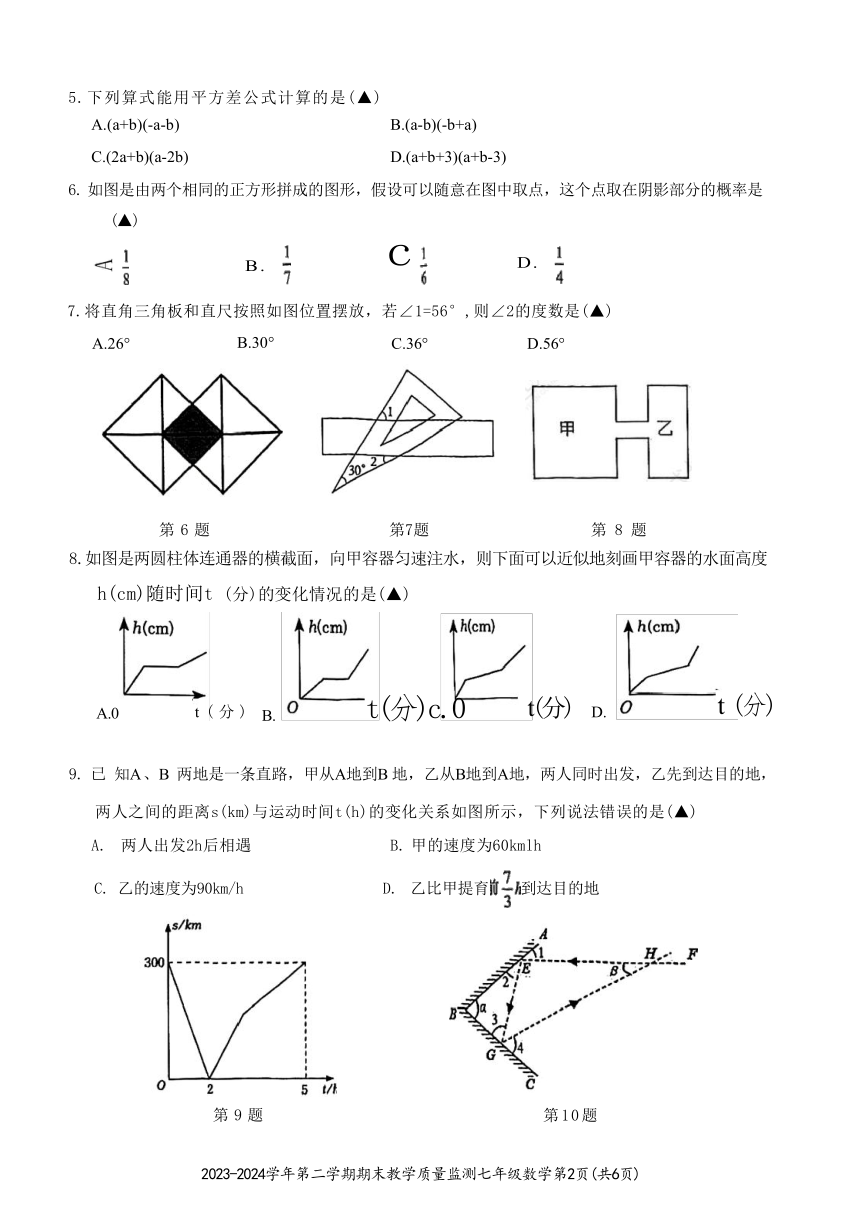
5.下列算式能用平方差公式计算的是(▲)
A.(a+b)(-a-b) B.(a-b)(-b+a)
C.(2a+b)(a-2b) D.(a+b+3)(a+b-3)
6. 如图是由两个相同的正方形拼成的图形,假设可以随意在图中取点,这个点取在阴影部分的概率是
(▲)
B. c D.
7.将直角三角板和直尺按照如图位置摆放,若∠1=56°,则∠2的度数是(▲)
A.26° B.30° C.36° D.56°
第 6 题 第7题 第 8 题
8.如图是两圆柱体连通器的横截面,向甲容器匀速注水,则下面可以近似地刻画甲容器的水面高度
h(cm)随时间t (分)的变化情况的是(▲)
A.0 t ( 分 ) B. t(分)c.0 t(分) D. t (分)
9. 已 知A 、B 两地是一条直路,甲从A地到B 地,乙从B地到A地,两人同时出发,乙先到达目的地,
两人之间的距离s(km)与运动时间t(h)的变化关系如图所示,下列说法错误的是(▲)
A. 两人出发2h后相遇 B. 甲的速度为60kmlh
C. 乙的速度为90km/h D. 乙比甲提育 到达目的地
第 9 题
第10题
2023-2024学年第二学期期末教学质量监测七年级数学第2页(共6页)
10.如图,两面镜子AB,BC 的夹角为∠α,当光线经过镜子后反射,∠1=∠2,∠3=∠4.若∠α=70°,
则∠β的度数是(▲)
A.30° B.35° C.40° D.45°
第二部分非选择题
二、填空题(本题共有5小题,每小题3分,共15分,请把答案填在答题卡上)
11.已知3”=2,3”=5,则3m-2n= ▲
12.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.聪聪每次摸球前先将袋子 里的球摇匀,任意摸出一个球记下颜色后再放回袋子,通过多次试验发现,摸出红球的频率稳定在
0.25的附近,则袋子中红球的个数可能是 ▲ 个.
13.如图,△ABC中,AD、AE 分别为角平分线和高,∠B=46°,∠C=64°,则∠DAE= ▲
14.如图,△ABC的周长为26,AC 的垂直平分线交BC于点D, 垂足为E,若AE=5, 则△ADB的周
长是
第 1 3 题
第14题
第15题
15.如图,在△ABC中,∠BAC=45°, 以BC为边向外作等腰直角三角形△BCD,连接AD,若AC=4,
则S△ACD ▲
三、解答题(第16题8分,第17题6分,第18题6分,第19题8分,第20题8分,第21题9分,
第22题10分,共55分)
16.(1)(π+2)0-3- +(-1)2024-|-2| (2)(-2xy) +(x y) ÷(-x y).
17.先化简,再求值:[(x+y) -(x+2y)(x-2y)]÷(-2y),其中x=1,y=-2.
2023-2024学年第二学期期末教学质量监测七年级数学第3页(共6页)
18.如图在6×5正方形网格中,每个小正方形的边长均为1,其顶点称为格点,点A 、B 、C 都在格点
上,请用无刻度直尺在给定的网格中作图.
图 1
( 1 ) 图 1 中S△ACB =
(2)在图1的格点中,作点B 关 于AC 的对称点B';
(3)在图2的格点中,作点D 使得△CAD≌△ACB.
图 2
19. 如图,在△ABC中,点D 在边BA的延长线上,过点D 作射线DM1/BC, 点 E 是射线DM 上 一 个定
点 .
(1)用尺规完成以下基本作图:在射线DM 上方作∠DEF=∠C, 与 BA 的延长线交于点F. (不写作法,
但保留作图痕迹)
(2)在(1)的条件下,若BD=AF, 求证: AC//FE, 请把以下的解题过程补充完整.
证明:∵DMI/BC ( 已 知 )
∴∠B=∠FDE( ① ),
∵BD=AF ( 已 知 ) ,
∴BD-AD= ② (等式的性质)
∴AB=FD,
在△ABC和△FDE 中 ,
∴.△ABC≌△FDE( ③ )
∴∠BAC= ④ (全等三角形的对应角相等),
∴AC//FE( ⑤ ).
2023-2024学年第二学期期末教学质量监测七年级数学第4页(共6页)
20.某港口某日从0时到12时的水深h(m)随时间t(1)变化的关系如图所示,船舶可以根据吃水深度选择 进出港口的时间,仔细观察图象,回答下列问题:
(1)当t= 时,该港口水深最浅;
(2)从 到 时,水深均在下降;
(3)当h=6时 ,t的值是
(4)某货船吃水深度为3m,它可以出入该港口的时间是
信息窗: ①吃水深度是指船舶的底部至船体与水 面相连处的垂直距离; ②该港口规定船舶进出港口时船底与港 口水底间的距离不能少于2m
21.阅读材料并回答下列问题:
材料一:我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.如图1可以得到
(a+b) ,(a-b) ,ab之间的等量关系是
材料二:换元法:是指引入一个或者几个新的变量代替原来的某些变量,通过引入新的变量将分散的条 件联系起来,变为熟悉的问题,其理论依据是等量代换。对于结构比较复杂的式子,可以把其 中某些部分看作整体,用新的字母代替(即整体换元),可以化繁为简从而找到解题的捷径, 请看以下例子:
若x满足(60-x)(x-40)=30,求(60-x) +(x-40) 的值.
解:设(60-x)=a,(x-40)=b, 则(60-x)(x-40)=ab=30,
a+b=(60-x)+(x-40)=
所以(60-x) +(x-40) =a +b =(a+b) -2ab=
问题:
(1)补全材料一、材料二中横线处;
(2)若x满足(2024-x) +(x-2023) =2025, 求(2024-x)(x-2023)的值;
(3)如图2,在长方形ABCD中 ,AB=14,BC=10, 点 E,F 分别是边AD,
AB上的点,且DE=BF=x, 分别以AE,AF 为边在长方形ABCD外侧
作正方形AEMN和正方形APQF, 若长方形AFGE的面积为60,求图中
两个正方形的面积之和,
(
a
)
图 1
图 2
2023-2024学年第二学期期末教学质量监测七年级数学第5页(共6页)
22. 【阅读理解】
中线是三角形中的重要线段之一.在利用中线解决几何问题时,当条件中出现“中点”、“中线” 等条件时,可以考虑做辅助线,即把中线延长一倍,通过构造全等三角形,把分散的已知条件和所要求 的结论集中到同一个三角形中,从而运用全等三角形的有关知识来解决问题,这种作辅助线的方法称为
“倍长中线法”
【初步感知】
(1)如图1,在△ABC 中 ,AB=6,AC=10,D 是 BC 的中点,求BC 边上的中线AD 的取值范围。小
明在组内经过合作交流,得到了如下的解决方法:
延长AD 到 点E, 使 DE=AD, 连 接BE. 可以判定△ADC丝△EDB, 从而得到AC=EB=10. 这样就
能把线段AB 、AC 、2AD 集中在△ABE中,利用三角形三边的关系,即可求出中线AD的取值范围是
(请直接写出答案)
【实践应用】
(2)为了测量学校旗杆AB 和教学楼CE 顶端之间的距离,学习小组设计了如图2所示的测量方案,他 们首先取地面BC 的中点D, 用测角仪测得此时∠ADE=90°, 测得旗杆高度AB=10.8m, 教学楼
高度CE=20.2m, 求 AE 的长 .
图 1
图 2
图 3
【拓展探究】
( 3 ) 如 图 3 , △ABD 和 △ACE 均为等腰直角三角形,连接DE,BC, 点 F 是 BC 的中点,连接FA 并
延长,与DE 相交于点G. 试探究: DE 和 AF 的数量关系和位置关系并说明理由.
2023-2024学年第二学期期末教学质量监测七年级数学第6页(共6页)
(
2024.07
)2023—2024学年第二学期期末教学质量监测 七年级数学试题
说明:1.答题前,请将学校、班级和姓名用规定的笔写在答题卷指定的位置上.
2.全卷分二部分,第一部分为选择题,第二部分为非选择题,共6页;考试时间90分钟,满分100
分 .
3. 本卷试题,考生必须在答题卡上作答;凡在试卷、草稿纸上作答的,其答案一律无效。答题 卡必须保持清洁,不能折叠.
4. 本卷选择题1~10,每小题选出答案后,用2B铅笔将答题卡选择题答题区内对应题目的答案标 号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案;非选择题11~22,答案(含作辅助
线)必须用规定的笔,按作答题目序号,写在答题卡非选择题答题区规定范围内. 5. 考试结束,请将答题卡交回.
第一部分选择题
一 、选择题(本题共有10小题,每小题3分,共30分.在每小题给出四个选项中,只有一项
是符合题目要求的,请将正确选项用2B铅笔填涂在答题卡上)
1. 我国新能源汽车发展势头迅猛,以下汽车车标融入了数学几何元素,其中是轴对称图形的是(▲)
A.
B.
C.
D.
2.红细胞是血液中数量最多的一种血细胞,它将氧气从肺送到身体各个组织,它的直径约为0.0000078m,
将0.0000078用科学记数法表示为(▲)
A.78×10·7 B.7.8×10·7 C.7.8×10·6 D.0.78×10·6
3. 下列计算正确的是(▲)
A.-m·(-m) =-m B.x ÷x =x4 C.(3x) =6x D.(-a ) =a
4.下列事件中,属于必然事件的是(▲)
A. 任意购买一张电影票,座位号是偶数
B. 梦到醒来会下雨,醒来后发现窗外在下雨
C. 解锁手机,提示微信收到了新消息
D. 随意掷一枚质地均匀的骰子,掷出的点数不超过6
2023-2024学年第二学期期末教学质量监测七年级数学第1页(共6页)
5.下列算式能用平方差公式计算的是(▲)
A.(a+b)(-a-b) B.(a-b)(-b+a)
C.(2a+b)(a-2b) D.(a+b+3)(a+b-3)
6. 如图是由两个相同的正方形拼成的图形,假设可以随意在图中取点,这个点取在阴影部分的概率是
(▲)
B. c D.
7.将直角三角板和直尺按照如图位置摆放,若∠1=56°,则∠2的度数是(▲)
A.26° B.30° C.36° D.56°
第 6 题 第7题 第 8 题
8.如图是两圆柱体连通器的横截面,向甲容器匀速注水,则下面可以近似地刻画甲容器的水面高度
h(cm)随时间t (分)的变化情况的是(▲)
A.0 t ( 分 ) B. t(分)c.0 t(分) D. t (分)
9. 已 知A 、B 两地是一条直路,甲从A地到B 地,乙从B地到A地,两人同时出发,乙先到达目的地,
两人之间的距离s(km)与运动时间t(h)的变化关系如图所示,下列说法错误的是(▲)
A. 两人出发2h后相遇 B. 甲的速度为60kmlh
C. 乙的速度为90km/h D. 乙比甲提育 到达目的地
第 9 题
第10题
2023-2024学年第二学期期末教学质量监测七年级数学第2页(共6页)
10.如图,两面镜子AB,BC 的夹角为∠α,当光线经过镜子后反射,∠1=∠2,∠3=∠4.若∠α=70°,
则∠β的度数是(▲)
A.30° B.35° C.40° D.45°
第二部分非选择题
二、填空题(本题共有5小题,每小题3分,共15分,请把答案填在答题卡上)
11.已知3”=2,3”=5,则3m-2n= ▲
12.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.聪聪每次摸球前先将袋子 里的球摇匀,任意摸出一个球记下颜色后再放回袋子,通过多次试验发现,摸出红球的频率稳定在
0.25的附近,则袋子中红球的个数可能是 ▲ 个.
13.如图,△ABC中,AD、AE 分别为角平分线和高,∠B=46°,∠C=64°,则∠DAE= ▲
14.如图,△ABC的周长为26,AC 的垂直平分线交BC于点D, 垂足为E,若AE=5, 则△ADB的周
长是
第 1 3 题
第14题
第15题
15.如图,在△ABC中,∠BAC=45°, 以BC为边向外作等腰直角三角形△BCD,连接AD,若AC=4,
则S△ACD ▲
三、解答题(第16题8分,第17题6分,第18题6分,第19题8分,第20题8分,第21题9分,
第22题10分,共55分)
16.(1)(π+2)0-3- +(-1)2024-|-2| (2)(-2xy) +(x y) ÷(-x y).
17.先化简,再求值:[(x+y) -(x+2y)(x-2y)]÷(-2y),其中x=1,y=-2.
2023-2024学年第二学期期末教学质量监测七年级数学第3页(共6页)
18.如图在6×5正方形网格中,每个小正方形的边长均为1,其顶点称为格点,点A 、B 、C 都在格点
上,请用无刻度直尺在给定的网格中作图.
图 1
( 1 ) 图 1 中S△ACB =
(2)在图1的格点中,作点B 关 于AC 的对称点B';
(3)在图2的格点中,作点D 使得△CAD≌△ACB.
图 2
19. 如图,在△ABC中,点D 在边BA的延长线上,过点D 作射线DM1/BC, 点 E 是射线DM 上 一 个定
点 .
(1)用尺规完成以下基本作图:在射线DM 上方作∠DEF=∠C, 与 BA 的延长线交于点F. (不写作法,
但保留作图痕迹)
(2)在(1)的条件下,若BD=AF, 求证: AC//FE, 请把以下的解题过程补充完整.
证明:∵DMI/BC ( 已 知 )
∴∠B=∠FDE( ① ),
∵BD=AF ( 已 知 ) ,
∴BD-AD= ② (等式的性质)
∴AB=FD,
在△ABC和△FDE 中 ,
∴.△ABC≌△FDE( ③ )
∴∠BAC= ④ (全等三角形的对应角相等),
∴AC//FE( ⑤ ).
2023-2024学年第二学期期末教学质量监测七年级数学第4页(共6页)
20.某港口某日从0时到12时的水深h(m)随时间t(1)变化的关系如图所示,船舶可以根据吃水深度选择 进出港口的时间,仔细观察图象,回答下列问题:
(1)当t= 时,该港口水深最浅;
(2)从 到 时,水深均在下降;
(3)当h=6时 ,t的值是
(4)某货船吃水深度为3m,它可以出入该港口的时间是
信息窗: ①吃水深度是指船舶的底部至船体与水 面相连处的垂直距离; ②该港口规定船舶进出港口时船底与港 口水底间的距离不能少于2m
21.阅读材料并回答下列问题:
材料一:我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.如图1可以得到
(a+b) ,(a-b) ,ab之间的等量关系是
材料二:换元法:是指引入一个或者几个新的变量代替原来的某些变量,通过引入新的变量将分散的条 件联系起来,变为熟悉的问题,其理论依据是等量代换。对于结构比较复杂的式子,可以把其 中某些部分看作整体,用新的字母代替(即整体换元),可以化繁为简从而找到解题的捷径, 请看以下例子:
若x满足(60-x)(x-40)=30,求(60-x) +(x-40) 的值.
解:设(60-x)=a,(x-40)=b, 则(60-x)(x-40)=ab=30,
a+b=(60-x)+(x-40)=
所以(60-x) +(x-40) =a +b =(a+b) -2ab=
问题:
(1)补全材料一、材料二中横线处;
(2)若x满足(2024-x) +(x-2023) =2025, 求(2024-x)(x-2023)的值;
(3)如图2,在长方形ABCD中 ,AB=14,BC=10, 点 E,F 分别是边AD,
AB上的点,且DE=BF=x, 分别以AE,AF 为边在长方形ABCD外侧
作正方形AEMN和正方形APQF, 若长方形AFGE的面积为60,求图中
两个正方形的面积之和,
(
a
)
图 1
图 2
2023-2024学年第二学期期末教学质量监测七年级数学第5页(共6页)
22. 【阅读理解】
中线是三角形中的重要线段之一.在利用中线解决几何问题时,当条件中出现“中点”、“中线” 等条件时,可以考虑做辅助线,即把中线延长一倍,通过构造全等三角形,把分散的已知条件和所要求 的结论集中到同一个三角形中,从而运用全等三角形的有关知识来解决问题,这种作辅助线的方法称为
“倍长中线法”
【初步感知】
(1)如图1,在△ABC 中 ,AB=6,AC=10,D 是 BC 的中点,求BC 边上的中线AD 的取值范围。小
明在组内经过合作交流,得到了如下的解决方法:
延长AD 到 点E, 使 DE=AD, 连 接BE. 可以判定△ADC丝△EDB, 从而得到AC=EB=10. 这样就
能把线段AB 、AC 、2AD 集中在△ABE中,利用三角形三边的关系,即可求出中线AD的取值范围是
(请直接写出答案)
【实践应用】
(2)为了测量学校旗杆AB 和教学楼CE 顶端之间的距离,学习小组设计了如图2所示的测量方案,他 们首先取地面BC 的中点D, 用测角仪测得此时∠ADE=90°, 测得旗杆高度AB=10.8m, 教学楼
高度CE=20.2m, 求 AE 的长 .
图 1
图 2
图 3
【拓展探究】
( 3 ) 如 图 3 , △ABD 和 △ACE 均为等腰直角三角形,连接DE,BC, 点 F 是 BC 的中点,连接FA 并
延长,与DE 相交于点G. 试探究: DE 和 AF 的数量关系和位置关系并说明理由.
2023-2024学年第二学期期末教学质量监测七年级数学第6页(共6页)
同课章节目录
