2024年四川省广元市中考数学真题试卷(含答案)
文档属性
| 名称 | 2024年四川省广元市中考数学真题试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 09:07:53 | ||
图片预览




文档简介
四川省广元市2024年中考数学真题试卷
说 明: 1. 全卷满分150分, 考试时间 120分钟.
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共三个大题26个小题.
3.考生必须在答题卡上答题,写在试卷上的答案无效.选择题必须使用2B铅笔填涂答案,非选择题必须使用0.5毫米黑色墨迹签字笔答题.
4.考试结束,将答题卡和试卷一并交回.
第Ⅰ卷 选择题 (共30分)
一、选择题(每小题给出的四个选项中,只有一个符合题意.每小题3分,共30分)
1.将-1在数轴上对应的点向右平移2个单位,则此时该点对应的数是
A. -1 B. 1
C. -3 D. 3
2.下列计算正确的是
3.一个几何体如图水平放置,它的俯视图是
4. 在“五·四”文艺晚会节目评选中, 某班选送的节目得分如下: 91, 96, 95, 92, 94,95,95,分析这组数据,下列说法错误的是
A. 中位数是95 B. 方差是3 C. 众数是95 D. 平均数是94
5. 如图, 已知四边形ABCD是⊙O的内接四边形, E为AD延长线上一点, ∠AOC=128°,则∠CDE等于
A. 64° B. 60°
C. 54° D. 52°
6.如果单项式 与单项式 的和仍是一个单项式,则在平面直角坐标系中点(m,n) 在
A. 第一象限 B.第二象限
C.第三象限 D.第四象限
7. 如图, 将△ABC绕点A顺时针旋转90°得到△ADE, 点B, C的对应点分别为点D, E,连接CE, 点D恰好落在线段CE上, 若 CD=3, BC=1, 则AD 的长为
A.
C. 2
8.我市把提升城市园林绿化水平作为推进城市更新行动的有效抓手,从 2023 年开始通过拆违建绿、见缝插绿等方式在全域打造多个小而美的“口袋公园”.现需要购买A、B两种绿植,已知A种绿植单价是B种绿植单价的3倍,用6750元购买的A种绿植比用3000元购买的B种绿植少50株.设B种绿植单价是x元,则可列方程是
9. 如图①, 在△ABC中, ∠ACB=90°, 点P从点A出发沿 A→C→B 以 Icm/s 的速度匀速运动至点 B, 图②是点 P运动时, △ABP的面积y(cm )随时间x(s)变化的函数图象,则该三角形的斜边AB的长为( )
A. 5 B. 7
10.如图,已知抛物线. 过点C(0,-2)与x轴交点的横坐标分别为x , x , 且-1①a-b+c<0; ②方程。 有两个不相等的实数根;③a+b>0;④a> ;⑤b -4ac>4a .其中正确的结论有
A. 1个 B. 2个
C. 3个 D. 4个
第Ⅱ卷 非选择题 (共120分)
二、填空题(把正确答案直接写在答题卡对应题目的横线上.每小题4分,共24分)
11. 分解因式:
12.2023年10月诺贝尔物理学奖授予三位“追光”科学家,以表彰他们“为研究物质中的电子动力学而产生阿秒光脉冲的实验方法”.什么是阿秒 1阿秒是10 秒,也就是十亿分之一秒的十亿分之一.目前世界上最短的单个阿秒光学脉冲是43阿秒.将43阿秒用科学记数法表示为 秒.
13. 点F是正五边形ABCDE边DE的中点, 连接BF 并延长与CD延长线交于点 G, 则∠BGC的度数为 .
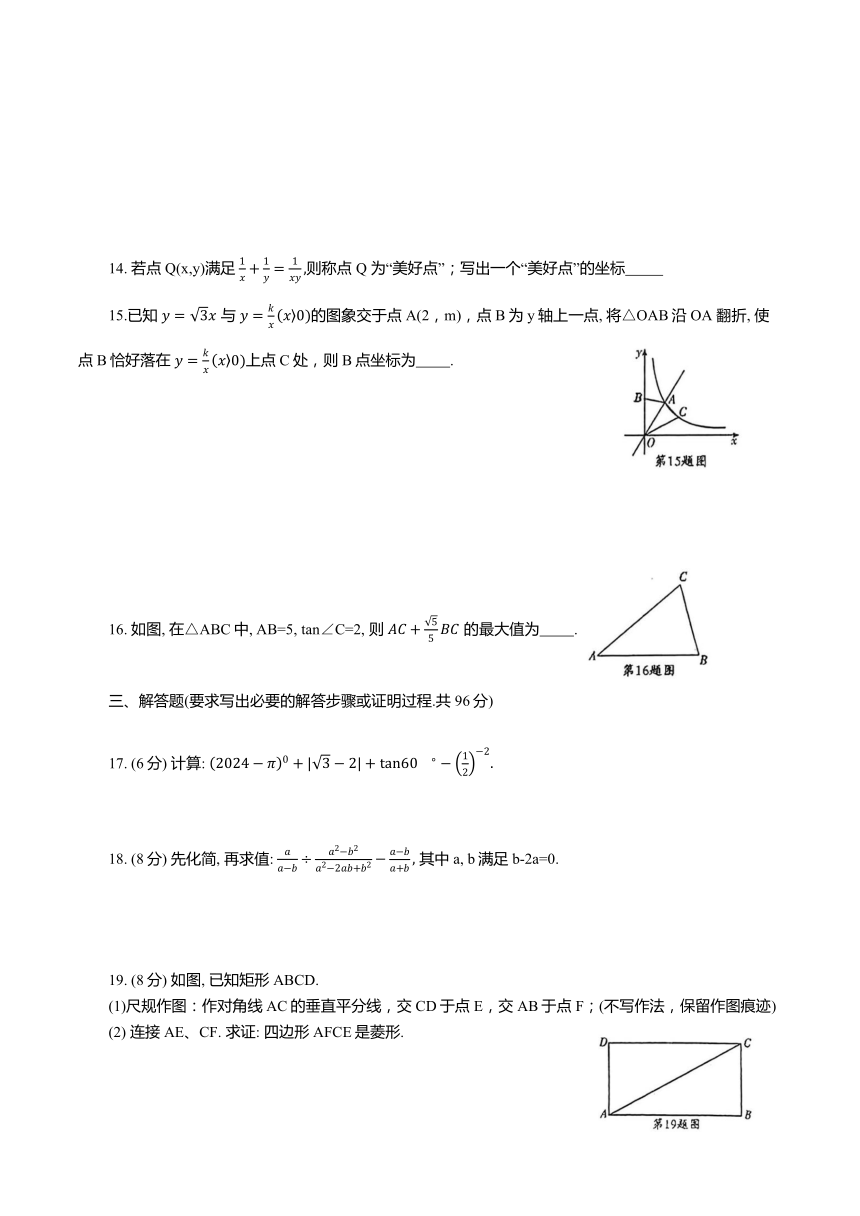
14. 若点Q(x,y)满足 则称点 Q 为“美好点”;写出一个“美好点”的坐标
15.已知 与 的图象交于点A(2,m),点B为y轴上一点, 将△OAB沿OA 翻折, 使点B恰好落在 上点C处,则B点坐标为 .
16. 如图, 在△ABC中, AB=5, tan∠C=2, 则 的最大值为 .
三、解答题(要求写出必要的解答步骤或证明过程.共96分)
17. (6分) 计算:
18. (8分) 先化简, 再求值: 其中a, b满足b-2a=0.
19. (8分) 如图, 已知矩形ABCD.
(1)尺规作图:作对角线AC的垂直平分线,交 CD于点 E,交AB于点 F;(不写作法,保留作图痕迹)
(2) 连接AE、CF. 求证: 四边形AFCE是菱形.
20.(9 分)广元市开展“蜀道少年”选拔活动,旨在让更多的青少年关注蜀道、了解蜀道、热爱蜀道、宣传蜀道,进一步挖掘和传承古蜀道文化、普及蜀道知识.为此某校开展了“蜀道文化知识竞赛”活动,并从全校学生中抽取了若干学生的竞赛成绩进行整理、描述和分析(竞赛成绩用x表示, 总分为100分, 共分成五个等级: A: 90≤x≤100; B: 80≤x<90; C: 70≤x<80; D: 60≤x<70; E: 50≤x<60). 并绘制了如下尚不完整的统计图.
抽取学生成绩等级人数统计表 抽取学生成绩等级扇形统计图
等级 A B C D E
人数 m 27 30 12 6
其中扇形图中C等级区域所对应的扇形的圆心角的度数是120°.
(1)样本容量为 ,m= ;
(2) 全校1200名学生中,请估计 A等级的人数;
(3)全校有5 名学生得满分,七年级1人,八年级2人,九年级2人,从这5名学生中任意选择两人在国旗下分享自己与蜀道的故事,请你用画树状图或列表的方法,求这两人来自同一个年级的概率.
21.(9 分)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值 叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为α,折射角为β,且 求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点 A,B,C,D 分别是长方体棱的中点,若光线经真空从矩形 A D D A 对角线交点 O 处射入,其折射光线恰好从点 C处射出. 如图②,已知α=60°, CD=10cm, 求截面ABCD 的面积.
22.(10分)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如下表:
价格/类别 短款 长款
进货价 (元/件) 80 90
销售价(元/件) 100 120
(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数:
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共 200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少
23.(10分)如图,已知反比例函数 和一次函数 的图象相交于点A(-3,a), 两点, O为坐标原点, 连接OA, OB.
(1) 求 与. 的解析式;
(2) 当. 时,请结合图象直接写出自变量x的取值范围;
(3) 求△AOB的面积.
24.(10分)如图, 在△ABC中, AC=BC, ∠ACB=90°, ⊙O经过A、C两点, 交AB于点D, CO的延长线交AB于点F, DE∥CF交BC于点E.
(1) 求证: DE为⊙O的切线;
(2) 若AC=4, tan∠CFD=2, 求⊙O的半径.
25.(12分)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.
在△ABC中, 点D为边AB上一点, 连接CD.
(1)初步探究
如图2, 若∠ACD=∠B, 求证:
(2)尝试应用
如图3, 在(1) 的条件下, 若点D为AB中点, BC=4, 求CD的长;
(3)创新提升
如图4,点E为CD中点,连接BE,若∠CDB=∠CBD=30°,∠ACD=∠EBD,AC=2 ,求 BE的长.
26. (14.分)在平面直角坐标系xOy中, 已知抛物线F: 经过点A(-3,-1),与y轴交于点B(0,2).
(1)求抛物线的函数表达式;
(2) 在直线AB上方抛物线上有一动点C,连接OC交AB于点D,求 的最大值及此时点 C的坐标;
(3)作抛物线 F 关于直线y=-1上一点的对称图象F',抛物线F与F'只有一个公共点E(点E在y轴右侧),G为直线AB上一点,H为抛物线F'对称轴上一点,若以B,E,G,H为顶点的四边形是平行四边形,求G点坐标.
参考答案及评分意见
说 明:1.解答题第17至26题中各步骤所标记分数为考生解答到这一步的累计分数。
2.参考答案都只给出一种解法,若考生的解答不同,请根据解答情况参考评分意见给分。
3.给分和扣分都以1分为基本单位。
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C B A D A C A C
二、填空题
11. (a-1) 12. 4.3×10 13. 18° 14. (2,-1)(答案不唯一)
15. (0,4) 16. 5
三、解答题
I7. 解: 原式 3分
=3-4
=-1 ’6分
18. 解: 原式
.. 5分
∵b-2a=0
∴b=2a
将其代入,原式 ’8分
19. 解: (1) 如图1所示: . ·3 分
(2) 证明: 如图2设EF与AC的交点为O, 由(1) 可知, 直线EF是线段AC的垂直平分线
∴EA=EC,FA=FC
∠COE=∠AOF=90°
OA=OC
又∵四边形ABCD是矩形
∴CD∥AB
∴∠ECO=∠FAO
∴△COE≌△AOF(ASA)
∴EC=FA
∴EA=EC=FA=FC
∴四边形AFCE是菱形……………………………………………`8分
20. 解: (1) 90 , 15 ;
(名) ……………… …4分
(3) 设七年级学生为A, 八年级学生为B ,B , 九年级学生为C ,C 答:全校1200名学生中,估计A等级的人数有200名……………………6分画树状图如下:
由树状图可知一共有20种等可能的结果,其中两人来自同一个年级的结果有4种,∴ P(选择的两人来自同一个年级)
21. 解: ·9分
∴如图,设 则c=4x, 由勾股定理得,
又∵β=30°,
∴折射率为:
(2) 由题意可得, α=60°, 折射率为, 4分
形ABCD是矩形, 点O是AD中点
又∵∠OCD=β
在Rt△ODC中, 设
由勾股定理得,
6分
又∵CD=10cm
∴截面ABCD的面积为: …9分
22.解:(1)设购进短款服装x件,购进长款服装y件,
由题意可得
解得
答:长款服装购进30件,短款服装购进20件………………………………4分
(2)设第二次购进m件短款服装,则购进(200-m)件长款服装,
由题意可得 80m+90(200-m)≤16800
解得:m≥120……………………………………………………………………6分
设利润为w元
则w=(100-80)m+(120-90)(200-m)=-10m+6000…………………………8分
∵-10<0
∴w随m的增大而减小,
∴当m=120时,
∴W最大=-10×120+6000=4800(元)………………………………………10分
答:当购进120件短款服装,80件长款服装时有最大利润,最大利润是4800元.
23. 解: (1) 由题知
∴a=3
.. ………………………………………………2分
把 代入 得
(2)由图象可知自变量x的取值范围为-3(3) 若AB与y轴相交于点C, ∴C (0, 1)
………………………………………10分
24. (1) 证明: 连接OD
∵AC=BC, ∠ACB=90°
∴△ACB为等腰直角三角形
∴∠CAB=45°
∵DE//CF
∴∠COD+∠EDO=180°
∴DE为⊙O的切线.………………………………………………………………4分
(2) 解: 过点C作CH⊥AB于点H
∵△ACB为等腰直角三角形, AC=4
∵tan∠CFD=2
7分
在Rt△FOD中,
设半径为r
……………… ………………………………10分
25. (1) 证明: ∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC
………………………………………………3分
(2) 解: ∵点D为AB中点
∴设AD-BD=m
由(1)知
∴△ACD与△ABC的相似比为
……………………………………7分
(3) 解:如图1过点C作EB的平行线交AB的延长线于点II.
∵点E为CD中点
∴设CE=DE=a
∵∠CDB=∠CBD=30°
∴CB=CD=2a, ∠DCB=120°
如图2, 过点B作BF⊥EC于点F.
∴∠FCB=60°
∴∠CBF=30°
∴EF=2a
如图1, ∵CH∥BE, 点E为CD中点
义∵∠ACD=∠EBD
∴∠ACD=∠H
△ACD∽△AHC
又
∴AD=2,AH=14
∴DH =12
即
……12
26. 罪: (1) A(-3.--1),B(0,2)代入.
得:
解得:
∴抛物线的函数表达式为 …………………………………………4分
(2) 如图1, 过点C作x轴的垂线交AB于点M.
∴CM ∥y轴
∴△CDM∽△ODB
设AB的解析式为y=mx+n
把A(-3,-1),B(0,2)代入解析式得
解得:
∴y=x+2
设 则M(1,1+2)
∵-3<1<0
时,
的最大值为 ,此时点C的坐标为( ··9分
(3)由中心对称可知,抛物线F与F'的公共点E为直线y=-1与抛物线F的右交点
(舍),
∴E({,-1) …………………………………………………………11分
∵抛物线F: 的顶点坐标为(-1,3)
∴抛物线 F' 的顶点坐标为(3,-5)
∴抛物线F'的对称轴为.x=3
如图2,当BE为对角线时
由题知
∴G(-2,0) 12分
如图3,当BE为边时
由题知.
∴G(2,4) ·13分
如图3, 由题知.
∴G(4,6)
综上:点G的坐标为(-2,0),(2,4),(4,6)………………………………………………14分
说 明: 1. 全卷满分150分, 考试时间 120分钟.
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共三个大题26个小题.
3.考生必须在答题卡上答题,写在试卷上的答案无效.选择题必须使用2B铅笔填涂答案,非选择题必须使用0.5毫米黑色墨迹签字笔答题.
4.考试结束,将答题卡和试卷一并交回.
第Ⅰ卷 选择题 (共30分)
一、选择题(每小题给出的四个选项中,只有一个符合题意.每小题3分,共30分)
1.将-1在数轴上对应的点向右平移2个单位,则此时该点对应的数是
A. -1 B. 1
C. -3 D. 3
2.下列计算正确的是
3.一个几何体如图水平放置,它的俯视图是
4. 在“五·四”文艺晚会节目评选中, 某班选送的节目得分如下: 91, 96, 95, 92, 94,95,95,分析这组数据,下列说法错误的是
A. 中位数是95 B. 方差是3 C. 众数是95 D. 平均数是94
5. 如图, 已知四边形ABCD是⊙O的内接四边形, E为AD延长线上一点, ∠AOC=128°,则∠CDE等于
A. 64° B. 60°
C. 54° D. 52°
6.如果单项式 与单项式 的和仍是一个单项式,则在平面直角坐标系中点(m,n) 在
A. 第一象限 B.第二象限
C.第三象限 D.第四象限
7. 如图, 将△ABC绕点A顺时针旋转90°得到△ADE, 点B, C的对应点分别为点D, E,连接CE, 点D恰好落在线段CE上, 若 CD=3, BC=1, 则AD 的长为
A.
C. 2
8.我市把提升城市园林绿化水平作为推进城市更新行动的有效抓手,从 2023 年开始通过拆违建绿、见缝插绿等方式在全域打造多个小而美的“口袋公园”.现需要购买A、B两种绿植,已知A种绿植单价是B种绿植单价的3倍,用6750元购买的A种绿植比用3000元购买的B种绿植少50株.设B种绿植单价是x元,则可列方程是
9. 如图①, 在△ABC中, ∠ACB=90°, 点P从点A出发沿 A→C→B 以 Icm/s 的速度匀速运动至点 B, 图②是点 P运动时, △ABP的面积y(cm )随时间x(s)变化的函数图象,则该三角形的斜边AB的长为( )
A. 5 B. 7
10.如图,已知抛物线. 过点C(0,-2)与x轴交点的横坐标分别为x , x , 且-1
A. 1个 B. 2个
C. 3个 D. 4个
第Ⅱ卷 非选择题 (共120分)
二、填空题(把正确答案直接写在答题卡对应题目的横线上.每小题4分,共24分)
11. 分解因式:
12.2023年10月诺贝尔物理学奖授予三位“追光”科学家,以表彰他们“为研究物质中的电子动力学而产生阿秒光脉冲的实验方法”.什么是阿秒 1阿秒是10 秒,也就是十亿分之一秒的十亿分之一.目前世界上最短的单个阿秒光学脉冲是43阿秒.将43阿秒用科学记数法表示为 秒.
13. 点F是正五边形ABCDE边DE的中点, 连接BF 并延长与CD延长线交于点 G, 则∠BGC的度数为 .
14. 若点Q(x,y)满足 则称点 Q 为“美好点”;写出一个“美好点”的坐标
15.已知 与 的图象交于点A(2,m),点B为y轴上一点, 将△OAB沿OA 翻折, 使点B恰好落在 上点C处,则B点坐标为 .
16. 如图, 在△ABC中, AB=5, tan∠C=2, 则 的最大值为 .
三、解答题(要求写出必要的解答步骤或证明过程.共96分)
17. (6分) 计算:
18. (8分) 先化简, 再求值: 其中a, b满足b-2a=0.
19. (8分) 如图, 已知矩形ABCD.
(1)尺规作图:作对角线AC的垂直平分线,交 CD于点 E,交AB于点 F;(不写作法,保留作图痕迹)
(2) 连接AE、CF. 求证: 四边形AFCE是菱形.
20.(9 分)广元市开展“蜀道少年”选拔活动,旨在让更多的青少年关注蜀道、了解蜀道、热爱蜀道、宣传蜀道,进一步挖掘和传承古蜀道文化、普及蜀道知识.为此某校开展了“蜀道文化知识竞赛”活动,并从全校学生中抽取了若干学生的竞赛成绩进行整理、描述和分析(竞赛成绩用x表示, 总分为100分, 共分成五个等级: A: 90≤x≤100; B: 80≤x<90; C: 70≤x<80; D: 60≤x<70; E: 50≤x<60). 并绘制了如下尚不完整的统计图.
抽取学生成绩等级人数统计表 抽取学生成绩等级扇形统计图
等级 A B C D E
人数 m 27 30 12 6
其中扇形图中C等级区域所对应的扇形的圆心角的度数是120°.
(1)样本容量为 ,m= ;
(2) 全校1200名学生中,请估计 A等级的人数;
(3)全校有5 名学生得满分,七年级1人,八年级2人,九年级2人,从这5名学生中任意选择两人在国旗下分享自己与蜀道的故事,请你用画树状图或列表的方法,求这两人来自同一个年级的概率.
21.(9 分)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值 叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为α,折射角为β,且 求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点 A,B,C,D 分别是长方体棱的中点,若光线经真空从矩形 A D D A 对角线交点 O 处射入,其折射光线恰好从点 C处射出. 如图②,已知α=60°, CD=10cm, 求截面ABCD 的面积.
22.(10分)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如下表:
价格/类别 短款 长款
进货价 (元/件) 80 90
销售价(元/件) 100 120
(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数:
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共 200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少
23.(10分)如图,已知反比例函数 和一次函数 的图象相交于点A(-3,a), 两点, O为坐标原点, 连接OA, OB.
(1) 求 与. 的解析式;
(2) 当. 时,请结合图象直接写出自变量x的取值范围;
(3) 求△AOB的面积.
24.(10分)如图, 在△ABC中, AC=BC, ∠ACB=90°, ⊙O经过A、C两点, 交AB于点D, CO的延长线交AB于点F, DE∥CF交BC于点E.
(1) 求证: DE为⊙O的切线;
(2) 若AC=4, tan∠CFD=2, 求⊙O的半径.
25.(12分)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.
在△ABC中, 点D为边AB上一点, 连接CD.
(1)初步探究
如图2, 若∠ACD=∠B, 求证:
(2)尝试应用
如图3, 在(1) 的条件下, 若点D为AB中点, BC=4, 求CD的长;
(3)创新提升
如图4,点E为CD中点,连接BE,若∠CDB=∠CBD=30°,∠ACD=∠EBD,AC=2 ,求 BE的长.
26. (14.分)在平面直角坐标系xOy中, 已知抛物线F: 经过点A(-3,-1),与y轴交于点B(0,2).
(1)求抛物线的函数表达式;
(2) 在直线AB上方抛物线上有一动点C,连接OC交AB于点D,求 的最大值及此时点 C的坐标;
(3)作抛物线 F 关于直线y=-1上一点的对称图象F',抛物线F与F'只有一个公共点E(点E在y轴右侧),G为直线AB上一点,H为抛物线F'对称轴上一点,若以B,E,G,H为顶点的四边形是平行四边形,求G点坐标.
参考答案及评分意见
说 明:1.解答题第17至26题中各步骤所标记分数为考生解答到这一步的累计分数。
2.参考答案都只给出一种解法,若考生的解答不同,请根据解答情况参考评分意见给分。
3.给分和扣分都以1分为基本单位。
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C B A D A C A C
二、填空题
11. (a-1) 12. 4.3×10 13. 18° 14. (2,-1)(答案不唯一)
15. (0,4) 16. 5
三、解答题
I7. 解: 原式 3分
=3-4
=-1 ’6分
18. 解: 原式
.. 5分
∵b-2a=0
∴b=2a
将其代入,原式 ’8分
19. 解: (1) 如图1所示: . ·3 分
(2) 证明: 如图2设EF与AC的交点为O, 由(1) 可知, 直线EF是线段AC的垂直平分线
∴EA=EC,FA=FC
∠COE=∠AOF=90°
OA=OC
又∵四边形ABCD是矩形
∴CD∥AB
∴∠ECO=∠FAO
∴△COE≌△AOF(ASA)
∴EC=FA
∴EA=EC=FA=FC
∴四边形AFCE是菱形……………………………………………`8分
20. 解: (1) 90 , 15 ;
(名) ……………… …4分
(3) 设七年级学生为A, 八年级学生为B ,B , 九年级学生为C ,C 答:全校1200名学生中,估计A等级的人数有200名……………………6分画树状图如下:
由树状图可知一共有20种等可能的结果,其中两人来自同一个年级的结果有4种,∴ P(选择的两人来自同一个年级)
21. 解: ·9分
∴如图,设 则c=4x, 由勾股定理得,
又∵β=30°,
∴折射率为:
(2) 由题意可得, α=60°, 折射率为, 4分
形ABCD是矩形, 点O是AD中点
又∵∠OCD=β
在Rt△ODC中, 设
由勾股定理得,
6分
又∵CD=10cm
∴截面ABCD的面积为: …9分
22.解:(1)设购进短款服装x件,购进长款服装y件,
由题意可得
解得
答:长款服装购进30件,短款服装购进20件………………………………4分
(2)设第二次购进m件短款服装,则购进(200-m)件长款服装,
由题意可得 80m+90(200-m)≤16800
解得:m≥120……………………………………………………………………6分
设利润为w元
则w=(100-80)m+(120-90)(200-m)=-10m+6000…………………………8分
∵-10<0
∴w随m的增大而减小,
∴当m=120时,
∴W最大=-10×120+6000=4800(元)………………………………………10分
答:当购进120件短款服装,80件长款服装时有最大利润,最大利润是4800元.
23. 解: (1) 由题知
∴a=3
.. ………………………………………………2分
把 代入 得
(2)由图象可知自变量x的取值范围为-3
………………………………………10分
24. (1) 证明: 连接OD
∵AC=BC, ∠ACB=90°
∴△ACB为等腰直角三角形
∴∠CAB=45°
∵DE//CF
∴∠COD+∠EDO=180°
∴DE为⊙O的切线.………………………………………………………………4分
(2) 解: 过点C作CH⊥AB于点H
∵△ACB为等腰直角三角形, AC=4
∵tan∠CFD=2
7分
在Rt△FOD中,
设半径为r
……………… ………………………………10分
25. (1) 证明: ∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC
………………………………………………3分
(2) 解: ∵点D为AB中点
∴设AD-BD=m
由(1)知
∴△ACD与△ABC的相似比为
……………………………………7分
(3) 解:如图1过点C作EB的平行线交AB的延长线于点II.
∵点E为CD中点
∴设CE=DE=a
∵∠CDB=∠CBD=30°
∴CB=CD=2a, ∠DCB=120°
如图2, 过点B作BF⊥EC于点F.
∴∠FCB=60°
∴∠CBF=30°
∴EF=2a
如图1, ∵CH∥BE, 点E为CD中点
义∵∠ACD=∠EBD
∴∠ACD=∠H
△ACD∽△AHC
又
∴AD=2,AH=14
∴DH =12
即
……12
26. 罪: (1) A(-3.--1),B(0,2)代入.
得:
解得:
∴抛物线的函数表达式为 …………………………………………4分
(2) 如图1, 过点C作x轴的垂线交AB于点M.
∴CM ∥y轴
∴△CDM∽△ODB
设AB的解析式为y=mx+n
把A(-3,-1),B(0,2)代入解析式得
解得:
∴y=x+2
设 则M(1,1+2)
∵-3<1<0
时,
的最大值为 ,此时点C的坐标为( ··9分
(3)由中心对称可知,抛物线F与F'的公共点E为直线y=-1与抛物线F的右交点
(舍),
∴E({,-1) …………………………………………………………11分
∵抛物线F: 的顶点坐标为(-1,3)
∴抛物线 F' 的顶点坐标为(3,-5)
∴抛物线F'的对称轴为.x=3
如图2,当BE为对角线时
由题知
∴G(-2,0) 12分
如图3,当BE为边时
由题知.
∴G(2,4) ·13分
如图3, 由题知.
∴G(4,6)
综上:点G的坐标为(-2,0),(2,4),(4,6)………………………………………………14分
同课章节目录
