六年级下册数学人教版比与比例(1)课件(共17张PPT)
文档属性
| 名称 | 六年级下册数学人教版比与比例(1)课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 624.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 05:26:00 | ||
图片预览




文档简介
(共17张PPT)
第五讲:比与比例
本讲聚焦
01
化简比与求比值
03
比的性质与比例的基本性质
05
比同分率间转换
02
比与比例的意义
04
复杂的比例分配
06
比例与图形的应用
07
正比例与反比例
考点分析
题型
填空题 、判断题、选择题外,生活情景,现代信息综合题,解决问题的应用题,比例和图形相关问题操作题
难度
基础知识占50~60,难度不大,但易错,易混,需要进行缜密计算,深入理解,精准计算
分值
题量不大,一般2~3小题,1道综合题,分值占10%左右
一.例题精讲
【比例基本性质的运用】
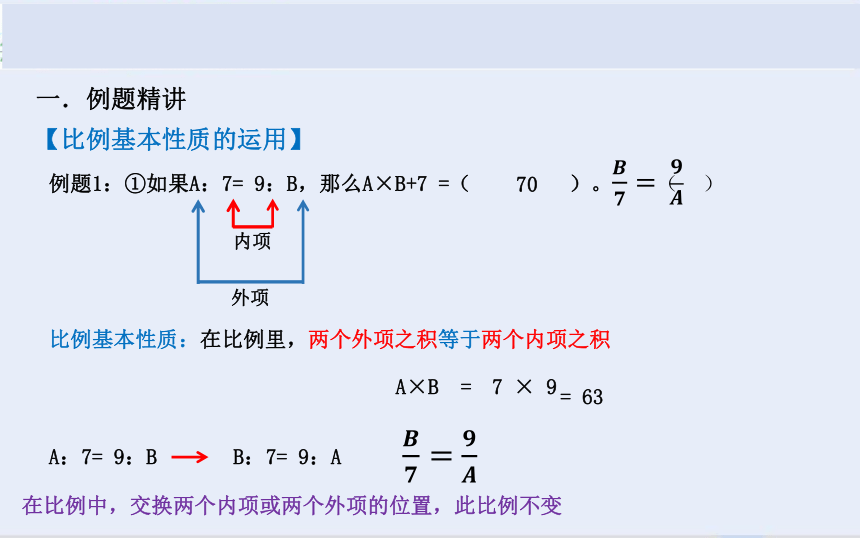
例题1:①如果A:7= 9:B,那么A×B+7 =( )。( )
外项
内项
比例基本性质:在比例里,两个外项之积等于两个内项之积
A×B =
7 × 9
= 63
70
A:7= 9:B B:7= 9:A
在比例中,交换两个内项或两个外项的位置,此比例不变
②已知三个数2、3、4,如果再添上一个数,使之能与已知三个数组成比例式,这个数应该是多少?
四个数 2 3 4 x
两两同为内项或外项
① 2×3=4x
② 2×4=3x
x=
x=
③ 2x=3×4
x=6
外项积=内项积
解:设:这个数为x
任意两个数的乘积除以第三个数得到比例中的第四个数
③在比例 2:0.3= 20:3中,如果第一项加上0.6,那么第三项应加上( ),比例仍然成立。
6
2 : 0.3 = 20 : 3
2.6:0.3 = x: 3
0.3x = 2.6×3
解:设第三项为x。
+0.6
2.6: 0.3 = : 3
0.3x = 7.8
x = 26
熟练运用比例基本性质,在比例里,外项积=内项积
26
+( )
6
x
外项积=内项积
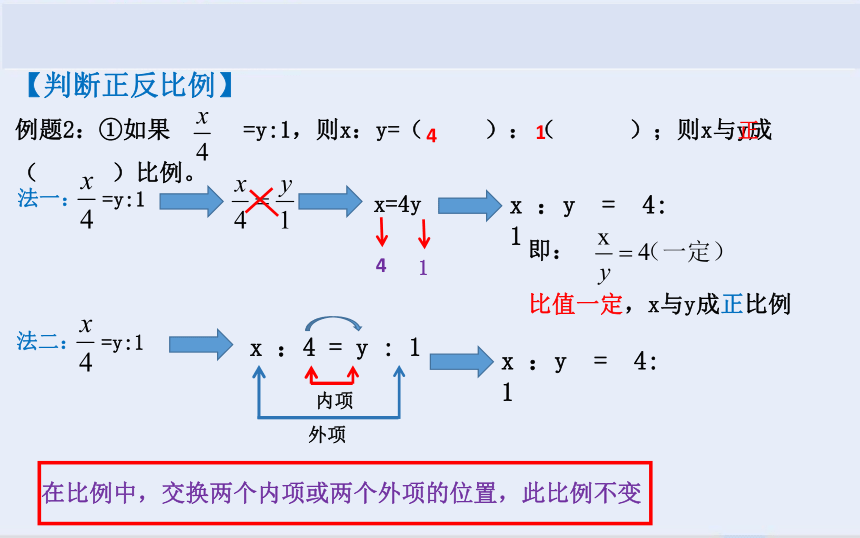
【判断正反比例】
例题2:①如果 =y:1,则x:y=( ):( );则x与y成( )比例。
内项
外项
4
1
正
1
4
x :4 = y : 1
=y:1
法二:
x :y = 4: 1
在比例中,交换两个内项或两个外项的位置,此比例不变
x :y = 4: 1
=y:1
法一:
x=4y
即:
比值一定,x与y成正比例
② =c,且b≠0,若a一定,b和c成( )比例;若b一定,a和c成( )比例。
= c
bc=a
乘积一定 ,b和c成反比例
比值一定, a和c成正比例
反
正
(一定)
=b
(一定)
【解比例】
例题3: ① ②
内项
外项
外项积等于内项积
= x : 8
【比例尺】
例题4:①比例尺=( ):( );比例尺实际上是一个( )。
图上距离
实际距离
比
比例尺
按表现形式分
按将实际距离放大还是缩小分
数值比例尺
线段比例尺
放大比例尺
缩小比例尺
(比值>1)
(比值<1)
例如:1 : 20 00000
例如:20 : 1
注意:比例尺中的图上距离和实际距离都是以厘米为单位的
②在比例尺是1:4000000的地图上,图上距离1厘米表示实际距离( )千米。也就是图上距离是实际距离的 。实际距离是图上距离的( )倍。
40
40 00000
40 00000
1:4000000 表示:图上1 cm 的距离相当于地面上40 00000 cm 的实际距离
40 00000 cm = 40 km
1
40 00000
÷
1
40 00000
÷
【比例应用题】
例题5:用一种方砖铺地, 铺120平方米需要用砖90块,如果铺80平方米,要用砖多少块 (用比例解答)。
解:设要用砖x块。
每块砖的面积(一定) =
答:要用砖60块。
等量关系式:每块砖的面积 = 每块砖的面积
=
(交叉相乘相等)
比值一定,成正比,用除法
例题6:一堆围棋子有黑白两种颜色,拿走15枚白棋子后,黑子与白子的个数之比为2:1;再拿走45枚黑棋子后,黑子与白子的个数比为1:5,求开始时黑棋子与白棋子各有多少枚?
= 10 : 5
= 1 : 5
黑 : 白
原来
2 : 1
现在
1 : 5
法一:
每份量:45÷(10-1)=5(枚)
原来黑子:10×5=50(枚)
原来白子:5×5+15=40(枚)
…
…
拿走15枚后剩下的白子数量不变
例题6:一堆围棋子有黑白两种颜色,拿走15枚白棋子后,黑子与白子的个数之比为2:1;再拿走45枚黑棋子后,黑子与白子的个数比为1:5,求开始时黑棋子与白棋子各有多少枚?
法二:
拿走15枚白棋子后 白棋子个数 为“1”
45÷(2- )=25(枚)
原来白子:25+15=40(枚)
原来黑子:25×2=50(枚)
答:开始黑子50枚,白子40枚。
则 原来黑子数量是剩下白子数量的 2×1=2
后来黑子数量是剩下白子数量的 ×1=
例题7:一个猎狗发现在离它8米远的前方有一只正在奔跑的小兔,就立刻追上去,已知猎狗跑2步的路程是小兔跑5步的路程,但是小兔的动作快,小兔跑5步的时间猎狗却只能跑3步。猎狗至少要跑出多少米才能追上小兔?
8米
答:猎狗至少要跑出24米才能追上小兔。
假设猎狗跑2步的路程为“1”
则:一步路程 猎狗:
小兔:
路程比:( ×3):( ×5)
= 3 : 2
3份
2份
每份量:8÷(3-2)=8(米)
8×3=24(米)
法一:
2、一个猎狗发现在离它8米远的前方有一只正在奔跑的小兔,就立刻追上去,已知猎狗跑2步的路程是小兔跑5步的路程,但是小兔的动作快,小兔跑5步的时间猎狗却只能跑3步。猎狗至少要跑出多少米才能追上小兔?
每份量:8÷(3-2)=8(米)
猎狗:8×3=24(米)
8米
法二:
(设数法)
假设猎狗一步跑5米,小兔一步跑2米
猎狗速度: 5×3=15(米)
小兔速度: 2×5=10(米)
猎狗 :小兔
速度: 15 :10 = 3:2
2份
3份
路程: 3 : 2
(时间相同,速度比=路程比)
谢谢观看
第五讲:比与比例
本讲聚焦
01
化简比与求比值
03
比的性质与比例的基本性质
05
比同分率间转换
02
比与比例的意义
04
复杂的比例分配
06
比例与图形的应用
07
正比例与反比例
考点分析
题型
填空题 、判断题、选择题外,生活情景,现代信息综合题,解决问题的应用题,比例和图形相关问题操作题
难度
基础知识占50~60,难度不大,但易错,易混,需要进行缜密计算,深入理解,精准计算
分值
题量不大,一般2~3小题,1道综合题,分值占10%左右
一.例题精讲
【比例基本性质的运用】
例题1:①如果A:7= 9:B,那么A×B+7 =( )。( )
外项
内项
比例基本性质:在比例里,两个外项之积等于两个内项之积
A×B =
7 × 9
= 63
70
A:7= 9:B B:7= 9:A
在比例中,交换两个内项或两个外项的位置,此比例不变
②已知三个数2、3、4,如果再添上一个数,使之能与已知三个数组成比例式,这个数应该是多少?
四个数 2 3 4 x
两两同为内项或外项
① 2×3=4x
② 2×4=3x
x=
x=
③ 2x=3×4
x=6
外项积=内项积
解:设:这个数为x
任意两个数的乘积除以第三个数得到比例中的第四个数
③在比例 2:0.3= 20:3中,如果第一项加上0.6,那么第三项应加上( ),比例仍然成立。
6
2 : 0.3 = 20 : 3
2.6:0.3 = x: 3
0.3x = 2.6×3
解:设第三项为x。
+0.6
2.6: 0.3 = : 3
0.3x = 7.8
x = 26
熟练运用比例基本性质,在比例里,外项积=内项积
26
+( )
6
x
外项积=内项积
【判断正反比例】
例题2:①如果 =y:1,则x:y=( ):( );则x与y成( )比例。
内项
外项
4
1
正
1
4
x :4 = y : 1
=y:1
法二:
x :y = 4: 1
在比例中,交换两个内项或两个外项的位置,此比例不变
x :y = 4: 1
=y:1
法一:
x=4y
即:
比值一定,x与y成正比例
② =c,且b≠0,若a一定,b和c成( )比例;若b一定,a和c成( )比例。
= c
bc=a
乘积一定 ,b和c成反比例
比值一定, a和c成正比例
反
正
(一定)
=b
(一定)
【解比例】
例题3: ① ②
内项
外项
外项积等于内项积
= x : 8
【比例尺】
例题4:①比例尺=( ):( );比例尺实际上是一个( )。
图上距离
实际距离
比
比例尺
按表现形式分
按将实际距离放大还是缩小分
数值比例尺
线段比例尺
放大比例尺
缩小比例尺
(比值>1)
(比值<1)
例如:1 : 20 00000
例如:20 : 1
注意:比例尺中的图上距离和实际距离都是以厘米为单位的
②在比例尺是1:4000000的地图上,图上距离1厘米表示实际距离( )千米。也就是图上距离是实际距离的 。实际距离是图上距离的( )倍。
40
40 00000
40 00000
1:4000000 表示:图上1 cm 的距离相当于地面上40 00000 cm 的实际距离
40 00000 cm = 40 km
1
40 00000
÷
1
40 00000
÷
【比例应用题】
例题5:用一种方砖铺地, 铺120平方米需要用砖90块,如果铺80平方米,要用砖多少块 (用比例解答)。
解:设要用砖x块。
每块砖的面积(一定) =
答:要用砖60块。
等量关系式:每块砖的面积 = 每块砖的面积
=
(交叉相乘相等)
比值一定,成正比,用除法
例题6:一堆围棋子有黑白两种颜色,拿走15枚白棋子后,黑子与白子的个数之比为2:1;再拿走45枚黑棋子后,黑子与白子的个数比为1:5,求开始时黑棋子与白棋子各有多少枚?
= 10 : 5
= 1 : 5
黑 : 白
原来
2 : 1
现在
1 : 5
法一:
每份量:45÷(10-1)=5(枚)
原来黑子:10×5=50(枚)
原来白子:5×5+15=40(枚)
…
…
拿走15枚后剩下的白子数量不变
例题6:一堆围棋子有黑白两种颜色,拿走15枚白棋子后,黑子与白子的个数之比为2:1;再拿走45枚黑棋子后,黑子与白子的个数比为1:5,求开始时黑棋子与白棋子各有多少枚?
法二:
拿走15枚白棋子后 白棋子个数 为“1”
45÷(2- )=25(枚)
原来白子:25+15=40(枚)
原来黑子:25×2=50(枚)
答:开始黑子50枚,白子40枚。
则 原来黑子数量是剩下白子数量的 2×1=2
后来黑子数量是剩下白子数量的 ×1=
例题7:一个猎狗发现在离它8米远的前方有一只正在奔跑的小兔,就立刻追上去,已知猎狗跑2步的路程是小兔跑5步的路程,但是小兔的动作快,小兔跑5步的时间猎狗却只能跑3步。猎狗至少要跑出多少米才能追上小兔?
8米
答:猎狗至少要跑出24米才能追上小兔。
假设猎狗跑2步的路程为“1”
则:一步路程 猎狗:
小兔:
路程比:( ×3):( ×5)
= 3 : 2
3份
2份
每份量:8÷(3-2)=8(米)
8×3=24(米)
法一:
2、一个猎狗发现在离它8米远的前方有一只正在奔跑的小兔,就立刻追上去,已知猎狗跑2步的路程是小兔跑5步的路程,但是小兔的动作快,小兔跑5步的时间猎狗却只能跑3步。猎狗至少要跑出多少米才能追上小兔?
每份量:8÷(3-2)=8(米)
猎狗:8×3=24(米)
8米
法二:
(设数法)
假设猎狗一步跑5米,小兔一步跑2米
猎狗速度: 5×3=15(米)
小兔速度: 2×5=10(米)
猎狗 :小兔
速度: 15 :10 = 3:2
2份
3份
路程: 3 : 2
(时间相同,速度比=路程比)
谢谢观看
