2024年黑龙江省牡丹江市中考数学真题(含答案)
文档属性
| 名称 | 2024年黑龙江省牡丹江市中考数学真题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 812.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 09:12:30 | ||
图片预览




文档简介
2024年黑龙江省牡丹江市中考数学试题
一、单项选择题(本题10个小题,每小题3分,共30分)
1.下列图形既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.下列计算正确的是( )
A.2a3 a2=2a6 B.(﹣2a)3÷b×=﹣8a3
C.(a3+a2+a)÷a=a2+a D.3a﹣2=
3.由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图所示,则搭建该几何体的方式有( )
A.1种 B.2种 C.3种 D.4种
4.某校八年级3班承担下周学校升旗任务,老师从备选的甲、乙、丙、丁四名同学中,选择两名担任升旗手,则甲、乙两名同学同时被选中的概率是( )
A. B. C. D.
5.如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为( )
A.100° B.110° C.120° D.130°
6.一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为( )
A.20% B.22% C.25% D.28%
7.如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个三角形,第3个图有10个三角形…按照此规律排列下去,第674个图中三角形的个数是( )
A.2022 B.2023 C.2024 D.2025
8.矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE,若四边形ODAF的面积为2,则k的值是( )
A. B. C. D.
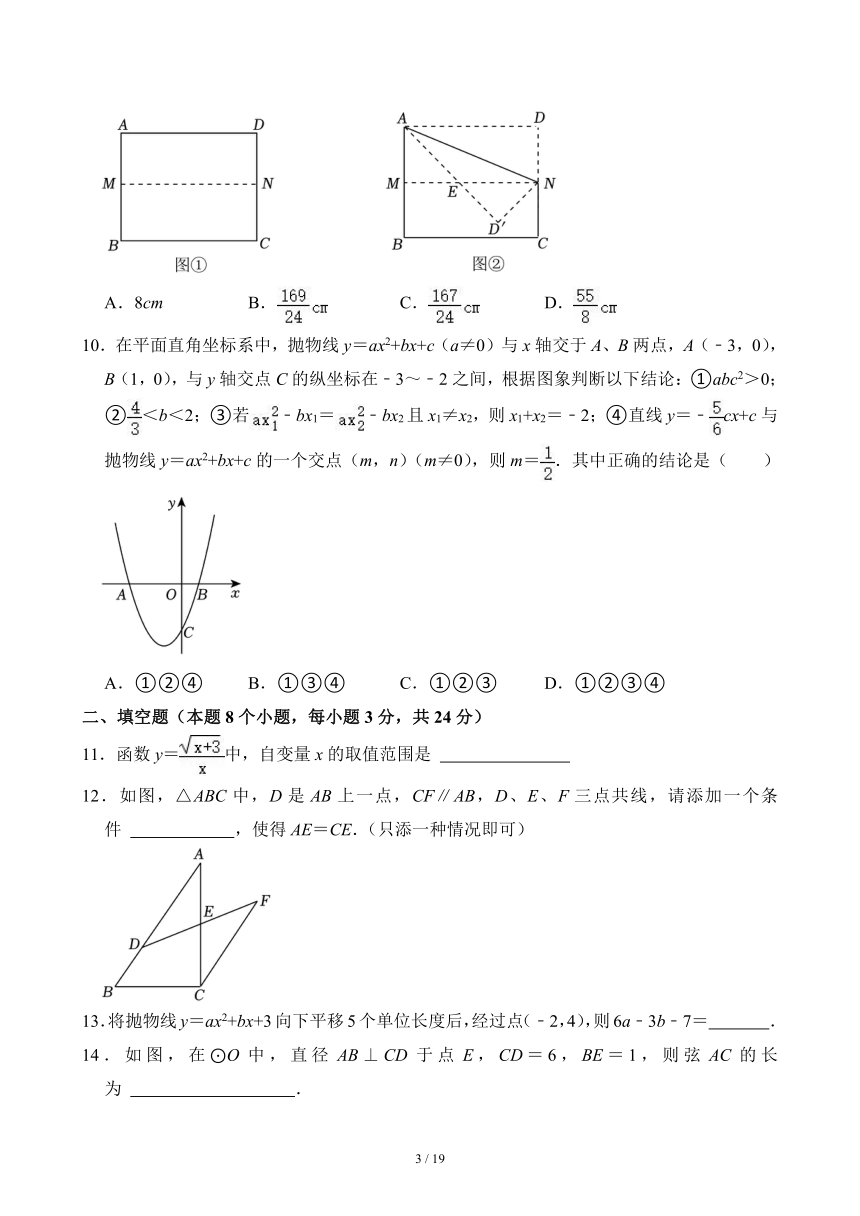
9.小明同学手中有一张矩形纸片ABCD,AD=12cm,CD=10cm,他进行了如下操作:
第一步,如图①,将矩形纸片对折,使AD与BC重合,得到折痕MN,将纸片展平.
第二步,如图②,再一次折叠纸片,把△ADN沿AN折叠得到△AD′N,AD′交折痕MN于点E,则线段EN的长为( )
A.8cm B. C. D.
10.在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,A(﹣3,0),B(1,0),与y轴交点C的纵坐标在﹣3~﹣2之间,根据图象判断以下结论:①abc2>0;②<b<2;③若﹣bx1=﹣bx2且x1≠x2,则x1+x2=﹣2;④直线y=﹣cx+c与抛物线y=ax2+bx+c的一个交点(m,n)(m≠0),则m=.其中正确的结论是( )
A.①②④ B.①③④ C.①②③ D.①②③④
二、填空题(本题8个小题,每小题3分,共24分)
11.函数y=中,自变量x的取值范围是
12.如图,△ABC中,D是AB上一点,CF∥AB,D、E、F三点共线,请添加一个条件 ,使得AE=CE.(只添一种情况即可)
13.将抛物线y=ax2+bx+3向下平移5个单位长度后,经过点(﹣2,4),则6a﹣3b﹣7= .
14.如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
15.已知一组正整数a,1,b,b,3有唯一众数8,中位数是5,则这一组数据的平均数为 .
16.若分式方程的解为正整数,则整数m的值为 .
17.矩形ABCD的面积是90,对角线AC,BD交于点O,点E是BC边的三等分点,连接DE,点P是DE的中点,OP=3,连接CP,则PC+PE的值为 .
18.如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF NF=AF BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 .
三、解答题(共66分)
19.先化简,再求值:÷(x﹣),并从﹣1,0,1,2,3中选一个合适的数代入求值.
20.如图,某数学活动小组用高度为1.5米的测角仪BC,对垂直于地面CD的建筑物AD的高度进行测量,BC⊥CD于点C.在B处测得A的仰角∠ABE=45°,然后将测角仪向建筑物方向水平移动6米至FG处,FG⊥CD于点G,测得A的仰角∠AFE=58°,BF的延长线交AD于点E,求建筑物AD的高度(结果保留小数点后一位).(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
21.某校为掌握学生对垃圾分类的了解情况,在全校范围内抽取部分学生进行调查问卷,并将收集到的信息进行整理,绘制成如图所示不完整的统计图,其中A为“非常了解”,B为“了解较多”,C为“基本了解”,D为“了解较少”.请你根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了 名学生;
(2)补全条形统计图,并求出扇形统计图中“了解较少”所对应的圆心角度数;
(3)若全校共有1200名学生,请估计全校有多少名学生“非常了解”垃圾分类问题.
22.在Rt△ACB中,∠ACB=90°,BC=12,AC=8,以BC为边向△ACB外作有一个内角为60°的菱形BCDE,对角线BD,CE交于点O,连接OA,请用尺规和三角板作出图形,并直接写出△AOC的面积.
23.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣3),连接BC.
(1)求该二次函数的解析式;
(2)点P是抛物线在第四象限图象上的任意一点,当△BCP的面积最大时,BC边上的高PN的值为 .
24.一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早小时到达目的地.甲、乙两车之间的路程y km与两车行驶时间xh的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,并在图中括号内填上正确的数;
(2)求图中线段EF所在直线的函数解析式(不要求写出自变量的取值范围);
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
25.数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= .
26.牡丹江某县市作为猴头菇生产的“黄金地带”,年总产量占全国总产量的50%以上,黑龙江省发布的“九珍十八品”名录将猴头菇列为首位.某商店准备在该地购进特级鲜品、特级干品两种猴头菇,购进鲜品猴头菇3箱、干品猴头菇2箱需420元,购进鲜品猴头菇4箱、干品猴头菇5箱需910元.请解答下列问题:
(1)特级鲜品猴头菇和特级干品猴头菇每箱的进价各是多少元?
(2)某商店计划同时购进特级鲜品猴头菇和特级干品猴头菇共80箱,特级鲜品猴头菇每箱售价定为50元,特级干品猴头菇每箱售价定为180元,全部销售后,获利不少于1560元,其中干品猴头菇不多于40箱,该商店有哪几种进货方案?
(3)在(2)的条件下,购进猴头菇全部售出,其中两种猴头菇各有1箱样品打a(a为正整数)折售出,最终获利1577元,请直接写出商店的进货方案.
27.如图,在平面直角坐标系中,直线y=x+b与x轴的正半轴交于点A,与y轴的负半轴交于点D,点B在x轴的正半轴上,四边形ABCD是平行四边形,线段OA的长是一元二次方程x2﹣4x﹣12=0的一个根.请解答下列问题:
(1)求点D的坐标;
(2)若线段BC的垂直平分线交直线AD于点E,交x轴于点F,交BC于点G,点E在第一象限,,连接BE,求tan∠ABE的值;
(3)在(2)的条件下,点M在直线DE上,在x轴上是否存在点N,使以E、M、N为顶点的三角形是直角边比为1:2的直角三角形?若存在,请直接写出△EMN的个数和其中两个点N的坐标;若不存在,请说明理由.
2024年黑龙江省牡丹江市中考数学试题参考答案
一、单项选择题(本题10个小题,每小题3分,共30分)
1.C 2.D 3.C 4.A 5.B
6.C 7.B 8.D 9.B 10.A
二、填空题(本题8个小题,每小题3分,共24分)
11.x≥﹣3且x≠0 12.(示例)DE=EF或AD=CF 13.2 14. 15.5 16.﹣1 17.13或 18.①②③⑤
三、解答题(共66分)
19.解:
=
=
=
=.
∵x≠0且x≠3,
∴x=﹣1或x=1或x=2.
当x=﹣1时,原式=.
20.解:根据题意可知四边形BEDC是矩形,
∴DE=BC=1.5m.
如图,∠ABE=45°,∠AFE=58°.
∵,
∴.
∵BE=EF+BF,
∴
∴AE≈16.
∴AD=AE+DE=17.5(米)
答:建筑物AD的高度约为17.5米.
21.解:(1)这次被调查的学生人数为:(20+8+5)÷(1﹣34%)=50(名);
(2)“了解较少”所对应的圆心角度数为:,
50×34%=17(人)
补全图形如下:
(3)(名),
估计全校有多少名学生“非常了解”垃圾分类问题有480名.
22.解:当∠CBE=60°时,所作图形如图,作OF⊥BC,垂足为F,
∵菱形BCDE,∠CBE=60°,
∴∠COB=90°,∠CBO=30°,∠OCB=60°,
∵BC=12,
∴,
∵∠OCB=60°,
∴∠COF=30°,
∴,
∴△AOC的面积为;
当∠BCD=60°时,所作图形如图,作OF⊥BC,垂足为F,如图2,
∵菱形BCDE,∠BCD=60°,
∴∠COB=90°,∠BCO=30°,
∵BC=12,
∴,,
∴,,
∴△AOC的面积为;
综上,△AOC的面积为12或36.
23.解:(1)把(﹣1,0)和(0,﹣3)代入得:
,
解得,
∴二次函数的解析式为;
(2)令y=0,则,
解得:x1=﹣1,x2=6,
∴点B的坐标为(6,0),
∴,
设直线BC的解析式为y=mx+n,代入得:
,
解得,
∴直线BC的解析式为,
过点P作PD⊥x轴交BC于点D,如图,
设点P的坐标为,则点D的坐标为,
∴,
∴,
∴△PBC最大为,
∴,
故答案为:.
24.解:(1)由图可知,甲车小时行驶的路程为(200﹣180)km,
∴甲车行驶的速度是,
70×(4+)=300(km),
填图如下:
故答案为:70;
(2)由图可知E,F的坐标分别为,(4,180),
设线段EF所在直线的函数解析式为y=kx+b,
则,
解得,
∴线段EF所在直线的函数解析式为y=120x﹣300;
(3)由题意知,A、C两地的距离为:,
乙车行驶的速度为:,
C、B两地的距离为:50×4=200(km),
A、B两地的距离为:300﹣200=100(km),
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况,当甲乙相遇前时:
200﹣50x=3(100﹣70x),
解得;
当甲乙相遇后时:
200﹣50x=3(70x﹣100),
解得;
综上可知,两车出发或时,乙车距B地的路程是甲车距B地路程的3倍.
25.(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.在AB边上截取AM=EF,连接DM.如图1,
∴∠B=90°﹣∠BAC=90°﹣30°=60°.
∵EF∥BC,
∴∠EFB=∠B=60°.
又∵∠EAD=60°,
∴∠EFB=∠EAD.
又∵∠BAD=∠EAD﹣∠EAF,∠AEF=∠EFB﹣∠EAF,
∴∠BAD=∠AEF.
又∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS).
∴AF=DM.
∴∠AMD=∠EFA=180°﹣∠EFB=180°﹣60°=120°.
∴∠BMD=180°﹣∠AMD=180°﹣120°=60°.
∵∠B=60°,
∴∠BMD=∠B=∠BDM.
∴△BMD是等边三角形.
∴BD=BM=DM,
∵AB=AM+BM,
∴AB=EF+BD;
(2)解:图②:AB=BD﹣EF,证明如下:
如图2.1所示,在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,
∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH﹣∠EAH=∠DAE﹣∠EAH,即∠BAE=∠HAD,
又∵AG=AF,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G,
∵BD∥EF,
∴∠ABC=∠F=∠G=60°,
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD﹣DH=BD﹣EF;
图③:AB=EF﹣BD,证明如下:
如图2.2所示,在EF上取点H使AH=AF,
∵EF∥BC,
∴∠F=∠ABC=60°,
∵AH=AF,
∴△AHF是等边三角形,
∴∠AHF=∠HAF=60°,
∴∠AHE=120°,
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB+∠EAH=180°﹣∠EAD﹣∠HAF=60°,
∵∠D+∠DAB=∠ABC=60°,
∴∠D=∠EAH,
∵∠DBA=180°﹣∠ABC=120°=∠EHA,
又∵AD=AE,
∴△EAH≌△ADB(AAS),
∴BD=AH,AB=EH,
∵AH=FH,
∴BD=HF,
∴AB=EH=EF﹣FH=EF﹣BD;
(3)解:如图3.1所示,
∵∠BAC=30°,∠C=90°,
∴AB=2BC,AB2=BC2+AC2,
∴,
∴BC=6,
∴AB=2BC=12,
∵CD=2BD,BC=BD+CD,
∴,
由(1)可知,BD+EF=AB,
∴EF=AB﹣BD=12﹣2=10;
如图3.2所示,当点D在线段BC的延长线上时,
∵CD<BD,与CD=2BD矛盾,
∴不符合题意;
如图3.3所示,当点D在线段CB的延长线上时,
∵CD=2BD=BD+BC,BC=6,
∴BD=BC=6,
由(2)可知,AB=EF﹣BD,
∵AB=2BC=12,
∴EF=AB+BD=12+6=18.
综上所述,EF=10或18,
故答案为:10或18.
26.解:(1)设特级鲜品猴头菇和特级干品猴头菇每箱的进价分别是x元和y元,
则,
解得:,
故特级鲜品猴头菇每箱进价为40元,特级干品猴头菇每箱进价为150元;
(2)解:设商店计划购进特级鲜品猴头菇m箱,则购进特级干品猴头菇(80﹣m)箱,
则,
解得:40≤m≤42,
∵m为正整数,
∴m=40,41,42,
故该商店有三种进货方案,
分别为:①购进特级鲜品猴头菇40箱,则购进特级干品猴头菇40箱;
②购进特级鲜品猴头菇41箱,则购进特级干品猴头菇39箱;
③购进特级鲜品猴头菇42箱,则购进特级干品猴头菇38箱;
(3)解:当购进特级鲜品猴头菇40箱,则购进特级干品猴头菇40箱时:
根据题意得(40﹣1)×(50﹣40)+(40﹣1)×(180﹣150)+(50 ﹣40)+(180 ﹣150)=1577,
解得:a=9;
当购进特级鲜品猴头菇41箱,则购进特级干品猴头菇39箱时:
根据题意得(41﹣1)×(50﹣40)+(39﹣1)×(180﹣150)+(50 ﹣40)+(180 ﹣150)=1577,
解得:a≈9.9(是小数,不符合要求);
当购进特级鲜品猴头菇42箱,则购进特级干品猴头菇38箱时:
根据题意得(42﹣1)×(50﹣40)+(38﹣1)×(180﹣150)+(50 ﹣40)+(180 ﹣150)=1577,
解得:a≈10.7(不符合要求);
故商店的进货方案是特级干品猴头菇40箱,特级鲜品猴头菇40箱.
27.解:(1)解方程x2﹣4x﹣12=0得x1=6,x2=﹣2,
∴OA=6,即点A的坐标为(6,0),
把(6,0)代入y=x+b得b=﹣6,
∴y=x﹣6,点D的坐标为(0,﹣6);
(2)过点E作EH⊥AB于点H,如图1,
∵OA=OD=6,
∴∠OAD=∠ODA=∠EAH=45°,,
∴,
又∵ABCD是平行四边形,
∴,AE∥BC,
∵GE是BC的垂直平分线,
∴,
∵AE∥BC,
∴∠EAF=∠GBF,∠AEF=∠FGB=90°,
∴△AEF≌△BGF,
∴BF=AF=2AH=6,
∴BH=AF+FB﹣AH=6+6﹣3=9,
∴;
(3)存在,12个,N1(0,0),N2(8,0),N3(10,0),N4(12,0),N5(18,0)(写出两个即可);理由如下:
如图2,当∠MEN=90°时,有4个,
∵∠EAN1=45°,
∴,
由(2)得AN1=6,OA=6,
∴ON1=12,
∴点N得坐标为(12,0);
当∠ENM=90°时,有4个,如图3,
当∠EMN=90°时,有4个,如图4,
∵∠N9AM9=45°,
∴,
∴,
∴点N9与O重合,
故点N9得坐标为(0,0),
综上所述,点△EMN的个数为12个,点N的坐标为N1(0,0),N2(8,0),N3(10,0),N4(12,0),N5(18,0)(写出两个即可).
一、单项选择题(本题10个小题,每小题3分,共30分)
1.下列图形既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.下列计算正确的是( )
A.2a3 a2=2a6 B.(﹣2a)3÷b×=﹣8a3
C.(a3+a2+a)÷a=a2+a D.3a﹣2=
3.由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图所示,则搭建该几何体的方式有( )
A.1种 B.2种 C.3种 D.4种
4.某校八年级3班承担下周学校升旗任务,老师从备选的甲、乙、丙、丁四名同学中,选择两名担任升旗手,则甲、乙两名同学同时被选中的概率是( )
A. B. C. D.
5.如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为( )
A.100° B.110° C.120° D.130°
6.一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为( )
A.20% B.22% C.25% D.28%
7.如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个三角形,第3个图有10个三角形…按照此规律排列下去,第674个图中三角形的个数是( )
A.2022 B.2023 C.2024 D.2025
8.矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE,若四边形ODAF的面积为2,则k的值是( )
A. B. C. D.
9.小明同学手中有一张矩形纸片ABCD,AD=12cm,CD=10cm,他进行了如下操作:
第一步,如图①,将矩形纸片对折,使AD与BC重合,得到折痕MN,将纸片展平.
第二步,如图②,再一次折叠纸片,把△ADN沿AN折叠得到△AD′N,AD′交折痕MN于点E,则线段EN的长为( )
A.8cm B. C. D.
10.在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,A(﹣3,0),B(1,0),与y轴交点C的纵坐标在﹣3~﹣2之间,根据图象判断以下结论:①abc2>0;②<b<2;③若﹣bx1=﹣bx2且x1≠x2,则x1+x2=﹣2;④直线y=﹣cx+c与抛物线y=ax2+bx+c的一个交点(m,n)(m≠0),则m=.其中正确的结论是( )
A.①②④ B.①③④ C.①②③ D.①②③④
二、填空题(本题8个小题,每小题3分,共24分)
11.函数y=中,自变量x的取值范围是
12.如图,△ABC中,D是AB上一点,CF∥AB,D、E、F三点共线,请添加一个条件 ,使得AE=CE.(只添一种情况即可)
13.将抛物线y=ax2+bx+3向下平移5个单位长度后,经过点(﹣2,4),则6a﹣3b﹣7= .
14.如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
15.已知一组正整数a,1,b,b,3有唯一众数8,中位数是5,则这一组数据的平均数为 .
16.若分式方程的解为正整数,则整数m的值为 .
17.矩形ABCD的面积是90,对角线AC,BD交于点O,点E是BC边的三等分点,连接DE,点P是DE的中点,OP=3,连接CP,则PC+PE的值为 .
18.如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF NF=AF BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 .
三、解答题(共66分)
19.先化简,再求值:÷(x﹣),并从﹣1,0,1,2,3中选一个合适的数代入求值.
20.如图,某数学活动小组用高度为1.5米的测角仪BC,对垂直于地面CD的建筑物AD的高度进行测量,BC⊥CD于点C.在B处测得A的仰角∠ABE=45°,然后将测角仪向建筑物方向水平移动6米至FG处,FG⊥CD于点G,测得A的仰角∠AFE=58°,BF的延长线交AD于点E,求建筑物AD的高度(结果保留小数点后一位).(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
21.某校为掌握学生对垃圾分类的了解情况,在全校范围内抽取部分学生进行调查问卷,并将收集到的信息进行整理,绘制成如图所示不完整的统计图,其中A为“非常了解”,B为“了解较多”,C为“基本了解”,D为“了解较少”.请你根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了 名学生;
(2)补全条形统计图,并求出扇形统计图中“了解较少”所对应的圆心角度数;
(3)若全校共有1200名学生,请估计全校有多少名学生“非常了解”垃圾分类问题.
22.在Rt△ACB中,∠ACB=90°,BC=12,AC=8,以BC为边向△ACB外作有一个内角为60°的菱形BCDE,对角线BD,CE交于点O,连接OA,请用尺规和三角板作出图形,并直接写出△AOC的面积.
23.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣3),连接BC.
(1)求该二次函数的解析式;
(2)点P是抛物线在第四象限图象上的任意一点,当△BCP的面积最大时,BC边上的高PN的值为 .
24.一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早小时到达目的地.甲、乙两车之间的路程y km与两车行驶时间xh的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,并在图中括号内填上正确的数;
(2)求图中线段EF所在直线的函数解析式(不要求写出自变量的取值范围);
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
25.数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= .
26.牡丹江某县市作为猴头菇生产的“黄金地带”,年总产量占全国总产量的50%以上,黑龙江省发布的“九珍十八品”名录将猴头菇列为首位.某商店准备在该地购进特级鲜品、特级干品两种猴头菇,购进鲜品猴头菇3箱、干品猴头菇2箱需420元,购进鲜品猴头菇4箱、干品猴头菇5箱需910元.请解答下列问题:
(1)特级鲜品猴头菇和特级干品猴头菇每箱的进价各是多少元?
(2)某商店计划同时购进特级鲜品猴头菇和特级干品猴头菇共80箱,特级鲜品猴头菇每箱售价定为50元,特级干品猴头菇每箱售价定为180元,全部销售后,获利不少于1560元,其中干品猴头菇不多于40箱,该商店有哪几种进货方案?
(3)在(2)的条件下,购进猴头菇全部售出,其中两种猴头菇各有1箱样品打a(a为正整数)折售出,最终获利1577元,请直接写出商店的进货方案.
27.如图,在平面直角坐标系中,直线y=x+b与x轴的正半轴交于点A,与y轴的负半轴交于点D,点B在x轴的正半轴上,四边形ABCD是平行四边形,线段OA的长是一元二次方程x2﹣4x﹣12=0的一个根.请解答下列问题:
(1)求点D的坐标;
(2)若线段BC的垂直平分线交直线AD于点E,交x轴于点F,交BC于点G,点E在第一象限,,连接BE,求tan∠ABE的值;
(3)在(2)的条件下,点M在直线DE上,在x轴上是否存在点N,使以E、M、N为顶点的三角形是直角边比为1:2的直角三角形?若存在,请直接写出△EMN的个数和其中两个点N的坐标;若不存在,请说明理由.
2024年黑龙江省牡丹江市中考数学试题参考答案
一、单项选择题(本题10个小题,每小题3分,共30分)
1.C 2.D 3.C 4.A 5.B
6.C 7.B 8.D 9.B 10.A
二、填空题(本题8个小题,每小题3分,共24分)
11.x≥﹣3且x≠0 12.(示例)DE=EF或AD=CF 13.2 14. 15.5 16.﹣1 17.13或 18.①②③⑤
三、解答题(共66分)
19.解:
=
=
=
=.
∵x≠0且x≠3,
∴x=﹣1或x=1或x=2.
当x=﹣1时,原式=.
20.解:根据题意可知四边形BEDC是矩形,
∴DE=BC=1.5m.
如图,∠ABE=45°,∠AFE=58°.
∵,
∴.
∵BE=EF+BF,
∴
∴AE≈16.
∴AD=AE+DE=17.5(米)
答:建筑物AD的高度约为17.5米.
21.解:(1)这次被调查的学生人数为:(20+8+5)÷(1﹣34%)=50(名);
(2)“了解较少”所对应的圆心角度数为:,
50×34%=17(人)
补全图形如下:
(3)(名),
估计全校有多少名学生“非常了解”垃圾分类问题有480名.
22.解:当∠CBE=60°时,所作图形如图,作OF⊥BC,垂足为F,
∵菱形BCDE,∠CBE=60°,
∴∠COB=90°,∠CBO=30°,∠OCB=60°,
∵BC=12,
∴,
∵∠OCB=60°,
∴∠COF=30°,
∴,
∴△AOC的面积为;
当∠BCD=60°时,所作图形如图,作OF⊥BC,垂足为F,如图2,
∵菱形BCDE,∠BCD=60°,
∴∠COB=90°,∠BCO=30°,
∵BC=12,
∴,,
∴,,
∴△AOC的面积为;
综上,△AOC的面积为12或36.
23.解:(1)把(﹣1,0)和(0,﹣3)代入得:
,
解得,
∴二次函数的解析式为;
(2)令y=0,则,
解得:x1=﹣1,x2=6,
∴点B的坐标为(6,0),
∴,
设直线BC的解析式为y=mx+n,代入得:
,
解得,
∴直线BC的解析式为,
过点P作PD⊥x轴交BC于点D,如图,
设点P的坐标为,则点D的坐标为,
∴,
∴,
∴△PBC最大为,
∴,
故答案为:.
24.解:(1)由图可知,甲车小时行驶的路程为(200﹣180)km,
∴甲车行驶的速度是,
70×(4+)=300(km),
填图如下:
故答案为:70;
(2)由图可知E,F的坐标分别为,(4,180),
设线段EF所在直线的函数解析式为y=kx+b,
则,
解得,
∴线段EF所在直线的函数解析式为y=120x﹣300;
(3)由题意知,A、C两地的距离为:,
乙车行驶的速度为:,
C、B两地的距离为:50×4=200(km),
A、B两地的距离为:300﹣200=100(km),
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况,当甲乙相遇前时:
200﹣50x=3(100﹣70x),
解得;
当甲乙相遇后时:
200﹣50x=3(70x﹣100),
解得;
综上可知,两车出发或时,乙车距B地的路程是甲车距B地路程的3倍.
25.(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.在AB边上截取AM=EF,连接DM.如图1,
∴∠B=90°﹣∠BAC=90°﹣30°=60°.
∵EF∥BC,
∴∠EFB=∠B=60°.
又∵∠EAD=60°,
∴∠EFB=∠EAD.
又∵∠BAD=∠EAD﹣∠EAF,∠AEF=∠EFB﹣∠EAF,
∴∠BAD=∠AEF.
又∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS).
∴AF=DM.
∴∠AMD=∠EFA=180°﹣∠EFB=180°﹣60°=120°.
∴∠BMD=180°﹣∠AMD=180°﹣120°=60°.
∵∠B=60°,
∴∠BMD=∠B=∠BDM.
∴△BMD是等边三角形.
∴BD=BM=DM,
∵AB=AM+BM,
∴AB=EF+BD;
(2)解:图②:AB=BD﹣EF,证明如下:
如图2.1所示,在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,
∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH﹣∠EAH=∠DAE﹣∠EAH,即∠BAE=∠HAD,
又∵AG=AF,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G,
∵BD∥EF,
∴∠ABC=∠F=∠G=60°,
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD﹣DH=BD﹣EF;
图③:AB=EF﹣BD,证明如下:
如图2.2所示,在EF上取点H使AH=AF,
∵EF∥BC,
∴∠F=∠ABC=60°,
∵AH=AF,
∴△AHF是等边三角形,
∴∠AHF=∠HAF=60°,
∴∠AHE=120°,
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB+∠EAH=180°﹣∠EAD﹣∠HAF=60°,
∵∠D+∠DAB=∠ABC=60°,
∴∠D=∠EAH,
∵∠DBA=180°﹣∠ABC=120°=∠EHA,
又∵AD=AE,
∴△EAH≌△ADB(AAS),
∴BD=AH,AB=EH,
∵AH=FH,
∴BD=HF,
∴AB=EH=EF﹣FH=EF﹣BD;
(3)解:如图3.1所示,
∵∠BAC=30°,∠C=90°,
∴AB=2BC,AB2=BC2+AC2,
∴,
∴BC=6,
∴AB=2BC=12,
∵CD=2BD,BC=BD+CD,
∴,
由(1)可知,BD+EF=AB,
∴EF=AB﹣BD=12﹣2=10;
如图3.2所示,当点D在线段BC的延长线上时,
∵CD<BD,与CD=2BD矛盾,
∴不符合题意;
如图3.3所示,当点D在线段CB的延长线上时,
∵CD=2BD=BD+BC,BC=6,
∴BD=BC=6,
由(2)可知,AB=EF﹣BD,
∵AB=2BC=12,
∴EF=AB+BD=12+6=18.
综上所述,EF=10或18,
故答案为:10或18.
26.解:(1)设特级鲜品猴头菇和特级干品猴头菇每箱的进价分别是x元和y元,
则,
解得:,
故特级鲜品猴头菇每箱进价为40元,特级干品猴头菇每箱进价为150元;
(2)解:设商店计划购进特级鲜品猴头菇m箱,则购进特级干品猴头菇(80﹣m)箱,
则,
解得:40≤m≤42,
∵m为正整数,
∴m=40,41,42,
故该商店有三种进货方案,
分别为:①购进特级鲜品猴头菇40箱,则购进特级干品猴头菇40箱;
②购进特级鲜品猴头菇41箱,则购进特级干品猴头菇39箱;
③购进特级鲜品猴头菇42箱,则购进特级干品猴头菇38箱;
(3)解:当购进特级鲜品猴头菇40箱,则购进特级干品猴头菇40箱时:
根据题意得(40﹣1)×(50﹣40)+(40﹣1)×(180﹣150)+(50 ﹣40)+(180 ﹣150)=1577,
解得:a=9;
当购进特级鲜品猴头菇41箱,则购进特级干品猴头菇39箱时:
根据题意得(41﹣1)×(50﹣40)+(39﹣1)×(180﹣150)+(50 ﹣40)+(180 ﹣150)=1577,
解得:a≈9.9(是小数,不符合要求);
当购进特级鲜品猴头菇42箱,则购进特级干品猴头菇38箱时:
根据题意得(42﹣1)×(50﹣40)+(38﹣1)×(180﹣150)+(50 ﹣40)+(180 ﹣150)=1577,
解得:a≈10.7(不符合要求);
故商店的进货方案是特级干品猴头菇40箱,特级鲜品猴头菇40箱.
27.解:(1)解方程x2﹣4x﹣12=0得x1=6,x2=﹣2,
∴OA=6,即点A的坐标为(6,0),
把(6,0)代入y=x+b得b=﹣6,
∴y=x﹣6,点D的坐标为(0,﹣6);
(2)过点E作EH⊥AB于点H,如图1,
∵OA=OD=6,
∴∠OAD=∠ODA=∠EAH=45°,,
∴,
又∵ABCD是平行四边形,
∴,AE∥BC,
∵GE是BC的垂直平分线,
∴,
∵AE∥BC,
∴∠EAF=∠GBF,∠AEF=∠FGB=90°,
∴△AEF≌△BGF,
∴BF=AF=2AH=6,
∴BH=AF+FB﹣AH=6+6﹣3=9,
∴;
(3)存在,12个,N1(0,0),N2(8,0),N3(10,0),N4(12,0),N5(18,0)(写出两个即可);理由如下:
如图2,当∠MEN=90°时,有4个,
∵∠EAN1=45°,
∴,
由(2)得AN1=6,OA=6,
∴ON1=12,
∴点N得坐标为(12,0);
当∠ENM=90°时,有4个,如图3,
当∠EMN=90°时,有4个,如图4,
∵∠N9AM9=45°,
∴,
∴,
∴点N9与O重合,
故点N9得坐标为(0,0),
综上所述,点△EMN的个数为12个,点N的坐标为N1(0,0),N2(8,0),N3(10,0),N4(12,0),N5(18,0)(写出两个即可).
同课章节目录
