四川省内江市第一中学2023-2024学年高二下学期6月月考数学(文)试题(含答案)
文档属性
| 名称 | 四川省内江市第一中学2023-2024学年高二下学期6月月考数学(文)试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 692.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 17:00:24 | ||
图片预览




文档简介
内江市第一中学2023-2024学年高二下学期6月月考
数学试题(文科)
考试时间:120分钟;满分150分;
一、单选题(共60分)
1.复数的虚部是( )
A.5 B. C. D.
2.抛物线的焦点坐标为( )
A. B. C. D.
3.下面几种推理过程中属于类比推理的是( )
A.两条直线平行,同旁内角互补,如果和是两条平行直线的同旁内角,则
B.科学家对比了火星和地球之间的某些相似特征,已知地球上有生命存在,所以猜测火星上也可能有生命存在
C.由,,,,,…,得出结论:一个偶数(大4)可以写成两个质数的和
D.在数列中,,,由此归纳出的通项公式
4.已知,则等于()
A. -4 B. 2 C. 1 D. -2
5.某单位为了落实“绿水青山就是金山银山”理念,制定节能减排的目标,先调查了用电量y(单位:kW·h)与气温x(单位:℃)之间的关系,随机选取了4天的用电量与当天气温,并制作了如下对照表:
x(单位:℃) 17 14 10
y(单位:kW·h) 24 34 38 a
由表中数据得线性回归方程:=-2x+60,则a的值为()
B.C. D.
6. “”是“方程表示双曲线”的()
A. 充分必要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
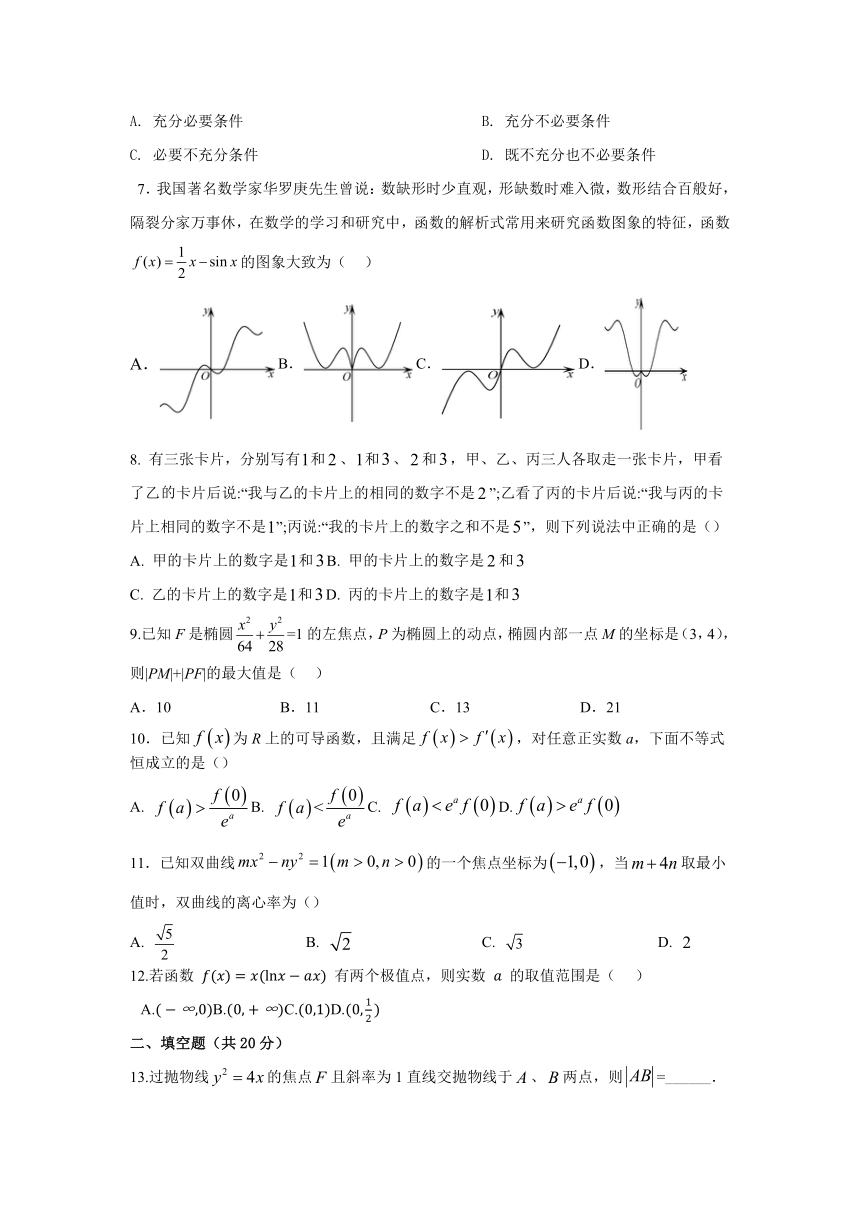
7.我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休,在数学的学习和研究中,函数的解析式常用来研究函数图象的特征,函数的图象大致为( )
B.C.D.
8. 有三张卡片,分别写有和、和、和,甲、乙、丙三人各取走一张卡片,甲看了乙卡片后说:“我与乙的卡片上的相同的数字不是”;乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是”;丙说:“我的卡片上的数字之和不是”,则下列说法中正确的是()
A. 甲的卡片上的数字是和B. 甲的卡片上的数字是和
C. 乙的卡片上的数字是和D. 丙的卡片上的数字是和
9.已知F是椭圆=1的左焦点,P为椭圆上的动点,椭圆内部一点M的坐标是(3,4),则|PM|+|PF|的最大值是( )
A.10 B.11 C.13 D.21
10.已知为R上的可导函数,且满足,对任意正实数a,下面不等式恒成立的是()
A. B. C. D.
11.已知双曲线的一个焦点坐标为,当取最小值时,双曲线的离心率为()
A. B. C. D.
12.若函数 有两个极值点,则实数 的取值范围是( )
A.B.C.D.
二、填空题(共20分)
13.过抛物线的焦点且斜率为1直线交抛物线于、两点,则=______.
14.若命题“ x∈R,x2﹣2x+m≤0”是假命题,则m的取值范围是___________.
15.已知F1,F2为椭圆的左 右焦点,点P在椭圆C上,,则___________.
16.若关于x的不等式对任意恒成立,则实数a的最大值是_______.
三、解答题(共70分)
17.(本题满分10分)
(1)求焦点在x轴上,长轴长为6,焦距为4的椭圆标准方程;
(2)求与双曲线有公共焦点,且过点的双曲线标准方程.
(本题满分12分)
已知函数,且函数在和处都取得极值.
(1)求实数与的值;
(2)对任意,方程存在三个实数根,求实数的取值范围.
19.(本题满分12分)
已知函数的图象过,在处的切线方程为.
(1)求函数的解析式;
(2)若关于的不等式在区间上恒成立,求实数的取值范围.
20.(本题满分12分)
“直播带货”是指通过一些互联网平台,使用直播技术进行商品线上展示、咨询答疑、导购销售的新型服务方式.某高校学生会调查了该校100名学生2020年在直播平台购物的情况,这100名学生中有男生60名,女生40名.男生中在直播平台购物的人数占男生总数的,女生中在直播平台购物的人数占女生总数的.
(1)填写列联表,并判断能否有99%的把握认为校学生的性别与2020年在直播平台购物有关
男生 女生 合计
2020年直播平台购物
2020年未在直播平台购物
合计
(2)若按照分层抽样的方法从所有男生中抽取6人,再从这6人中随机抽取3人,求恰有2人在直播平台购物的概率
参考附表:
0.10 0.01 0.001
2.706 6.635 10.828
参考公式:,.
21.(本题满分12分)
已知抛物线 的准线与y轴的交点为 .
(1)求 的方程,若经点的直线与C有且只有一个公共点时,求直线的方程.
(2)若过点 的直线 与抛物线 交于 两点.求证: 为定值.
22.(本题满分12分)
已知函数,其中.
(1)讨论函数的单调性;
(2)当时,若满足,证明:.
22.(本题满分12分)
已知函数
(1)求的单调区间;
(2)当b=1时,若对任意的,都有恒成立,求的取值范围.
参考答案:
1.B
2.D
3.A
4.A
5.D
6.C
7.A
8.D
9.C
10.B
11.B
12.C
13.1
【详解】展开式的通项为,令解得,∴.
∴.
故答案为:1
14.
【详解】由椭圆定义可得|PF1|+|PF2|=4,利用余弦定理可得|PF1|2+|PF2|2-2|PF1|·|PF2|·cos 60°=|F1F2|2,
所以,
解得3|PF1|·|PF2|=4,即,
故答案为:
15.1979
【详解】由信息(1)列举出满足条件的所有可能的四位数,共有五种,分别是:1997,1979,
9791,9719,7199.
若这个数是1997,则与7991有两个位置的数字相同,与信息(2)矛盾;
若这个数是1979,则满足信息(2);
若这个数是9791,则与7991有两个位置的数字相同,与信息(2)矛盾;
若这个数是9719,则与7991四个个位置的数字均不同,与信息(2)矛盾;
若这个数是7199,则与7991有两个位置的数字相同,与信息(2)矛盾.
综上可得这个四位数只能是1979.
16.
【详解】由可得,,令,,
故在上单增,.令且,,当时,单增,
当或,单减.
又等价于,
当时,恒成立,;
当时,可得,即,;
当时,可得 ,又时,,.
综上,,故a的最大值是.
故答案为:.
17.椭圆的标准方程为;双曲线的标准方程为:.
【详解】设椭圆标准方程为,则
焦距为4,长轴长为6,
,,,椭圆标准方程为;
双曲线双曲线的焦点为,
设双曲线的方程为,
可得,
将点代入双曲线方程可得,,
解得,,
即有所求双曲线的方程为:.
18.(1)表格见解析,有;
(2)分布列见解析,.
(1)
解:由题意可得关于对教师教学水平和教师管理水平评价的22列联表:
对教师管理水平满意 对教师管理水平不满意 合计
对教师教学水平满意 40 20 60
对教师教学水平不满意 35 5 40
合计 75 25 100
,
所以有97.5%的把握认为教师教学水平满意与教师管理水平满意有关;
(2)
解:对教师教学水平和教师管理水平都满意的概率为,且随机变量X的所有可能取值为0,1,2,3,
其中;;;;
所以随机变量X的分布列为:
X 0 1 2 3
P
则.
19.(1),(2)
【详解】解:(1)由,得,
因为在处的切线方程为,
所以,,
所以,
因为函数的图像过,
所以,所以解得,
所以,
(2)令,则
,令,即,得或,
当时,,当时,,
所以在上递增,在上递减,
因为,,
所以的最小值为
要不等式在区间上恒成立,只要在区间上恒成立,
所以只要,所以,
所以实数的取值范围为
20.(1)证明见解析;(2).
【详解】(1)取中点,连接、,
,为的中点,则, ,
平面,平面平面,平面平面,
平面,
平面,,
又,四边形是平行四边形,,
是等边三角形,,
平面,平面平面,平面平面,
平面,平面,
平面,平面平面;
(2)由(1)得平面,又平面,,
又,,
以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、,
平面的一个法向量为,
设平面的一个法向量为,,,
则,取,得,
设平面与平面所成锐二面角的平面角为,则.
因此,平面与平面所成锐二面角的余弦值为.
21.(1)
(2)存在,
(1)
圆的圆心为,半径为4,
∵线段的垂直平分线与线段交于点,∴,
因为在圆的内部,又,
∴
∴点的轨迹是以为焦点的椭圆,长轴长,半焦距,
∴,短半轴长
∴点的轨迹方程为
(2)
假设存在常数λ,使恒成立,则,
①当l1,l2中一条斜率不存在时,可知|AB|,|CD|其中一个长为2a=4,另一个为,
此时,
②当l1,l2的斜率存在且不为0时,不妨设l1:x=ty+1(t≠0),,
,
联立得
∴,,
∴,
用代替上式中的t可得,,
∴,
综上所述,存在常数使得恒成立.
22.(1)答案见解析;(2)证明见解析.
【详解】解:(1)函数的定义域为,.
①当时,则当时,恒成立
在上单调递减,无单调递增区间;
②当时,则由得
当时,;
当时,.
在上单调递减,在上单调递增,
综上所述,当时,在上单调递减,无单调递增区间;
当时,在上单调递减,在上单调递增.
(2),.
满足,
,
即
欲证,
即证,
即证,又,,即证
亦证
即
即证
设,即证.
设.
在上恒成立,
在上单调递减,
.
.
即成立
答案第1页,共2页
数学试题(文科)
考试时间:120分钟;满分150分;
一、单选题(共60分)
1.复数的虚部是( )
A.5 B. C. D.
2.抛物线的焦点坐标为( )
A. B. C. D.
3.下面几种推理过程中属于类比推理的是( )
A.两条直线平行,同旁内角互补,如果和是两条平行直线的同旁内角,则
B.科学家对比了火星和地球之间的某些相似特征,已知地球上有生命存在,所以猜测火星上也可能有生命存在
C.由,,,,,…,得出结论:一个偶数(大4)可以写成两个质数的和
D.在数列中,,,由此归纳出的通项公式
4.已知,则等于()
A. -4 B. 2 C. 1 D. -2
5.某单位为了落实“绿水青山就是金山银山”理念,制定节能减排的目标,先调查了用电量y(单位:kW·h)与气温x(单位:℃)之间的关系,随机选取了4天的用电量与当天气温,并制作了如下对照表:
x(单位:℃) 17 14 10
y(单位:kW·h) 24 34 38 a
由表中数据得线性回归方程:=-2x+60,则a的值为()
B.C. D.
6. “”是“方程表示双曲线”的()
A. 充分必要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
7.我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休,在数学的学习和研究中,函数的解析式常用来研究函数图象的特征,函数的图象大致为( )
B.C.D.
8. 有三张卡片,分别写有和、和、和,甲、乙、丙三人各取走一张卡片,甲看了乙卡片后说:“我与乙的卡片上的相同的数字不是”;乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是”;丙说:“我的卡片上的数字之和不是”,则下列说法中正确的是()
A. 甲的卡片上的数字是和B. 甲的卡片上的数字是和
C. 乙的卡片上的数字是和D. 丙的卡片上的数字是和
9.已知F是椭圆=1的左焦点,P为椭圆上的动点,椭圆内部一点M的坐标是(3,4),则|PM|+|PF|的最大值是( )
A.10 B.11 C.13 D.21
10.已知为R上的可导函数,且满足,对任意正实数a,下面不等式恒成立的是()
A. B. C. D.
11.已知双曲线的一个焦点坐标为,当取最小值时,双曲线的离心率为()
A. B. C. D.
12.若函数 有两个极值点,则实数 的取值范围是( )
A.B.C.D.
二、填空题(共20分)
13.过抛物线的焦点且斜率为1直线交抛物线于、两点,则=______.
14.若命题“ x∈R,x2﹣2x+m≤0”是假命题,则m的取值范围是___________.
15.已知F1,F2为椭圆的左 右焦点,点P在椭圆C上,,则___________.
16.若关于x的不等式对任意恒成立,则实数a的最大值是_______.
三、解答题(共70分)
17.(本题满分10分)
(1)求焦点在x轴上,长轴长为6,焦距为4的椭圆标准方程;
(2)求与双曲线有公共焦点,且过点的双曲线标准方程.
(本题满分12分)
已知函数,且函数在和处都取得极值.
(1)求实数与的值;
(2)对任意,方程存在三个实数根,求实数的取值范围.
19.(本题满分12分)
已知函数的图象过,在处的切线方程为.
(1)求函数的解析式;
(2)若关于的不等式在区间上恒成立,求实数的取值范围.
20.(本题满分12分)
“直播带货”是指通过一些互联网平台,使用直播技术进行商品线上展示、咨询答疑、导购销售的新型服务方式.某高校学生会调查了该校100名学生2020年在直播平台购物的情况,这100名学生中有男生60名,女生40名.男生中在直播平台购物的人数占男生总数的,女生中在直播平台购物的人数占女生总数的.
(1)填写列联表,并判断能否有99%的把握认为校学生的性别与2020年在直播平台购物有关
男生 女生 合计
2020年直播平台购物
2020年未在直播平台购物
合计
(2)若按照分层抽样的方法从所有男生中抽取6人,再从这6人中随机抽取3人,求恰有2人在直播平台购物的概率
参考附表:
0.10 0.01 0.001
2.706 6.635 10.828
参考公式:,.
21.(本题满分12分)
已知抛物线 的准线与y轴的交点为 .
(1)求 的方程,若经点的直线与C有且只有一个公共点时,求直线的方程.
(2)若过点 的直线 与抛物线 交于 两点.求证: 为定值.
22.(本题满分12分)
已知函数,其中.
(1)讨论函数的单调性;
(2)当时,若满足,证明:.
22.(本题满分12分)
已知函数
(1)求的单调区间;
(2)当b=1时,若对任意的,都有恒成立,求的取值范围.
参考答案:
1.B
2.D
3.A
4.A
5.D
6.C
7.A
8.D
9.C
10.B
11.B
12.C
13.1
【详解】展开式的通项为,令解得,∴.
∴.
故答案为:1
14.
【详解】由椭圆定义可得|PF1|+|PF2|=4,利用余弦定理可得|PF1|2+|PF2|2-2|PF1|·|PF2|·cos 60°=|F1F2|2,
所以,
解得3|PF1|·|PF2|=4,即,
故答案为:
15.1979
【详解】由信息(1)列举出满足条件的所有可能的四位数,共有五种,分别是:1997,1979,
9791,9719,7199.
若这个数是1997,则与7991有两个位置的数字相同,与信息(2)矛盾;
若这个数是1979,则满足信息(2);
若这个数是9791,则与7991有两个位置的数字相同,与信息(2)矛盾;
若这个数是9719,则与7991四个个位置的数字均不同,与信息(2)矛盾;
若这个数是7199,则与7991有两个位置的数字相同,与信息(2)矛盾.
综上可得这个四位数只能是1979.
16.
【详解】由可得,,令,,
故在上单增,.令且,,当时,单增,
当或,单减.
又等价于,
当时,恒成立,;
当时,可得,即,;
当时,可得 ,又时,,.
综上,,故a的最大值是.
故答案为:.
17.椭圆的标准方程为;双曲线的标准方程为:.
【详解】设椭圆标准方程为,则
焦距为4,长轴长为6,
,,,椭圆标准方程为;
双曲线双曲线的焦点为,
设双曲线的方程为,
可得,
将点代入双曲线方程可得,,
解得,,
即有所求双曲线的方程为:.
18.(1)表格见解析,有;
(2)分布列见解析,.
(1)
解:由题意可得关于对教师教学水平和教师管理水平评价的22列联表:
对教师管理水平满意 对教师管理水平不满意 合计
对教师教学水平满意 40 20 60
对教师教学水平不满意 35 5 40
合计 75 25 100
,
所以有97.5%的把握认为教师教学水平满意与教师管理水平满意有关;
(2)
解:对教师教学水平和教师管理水平都满意的概率为,且随机变量X的所有可能取值为0,1,2,3,
其中;;;;
所以随机变量X的分布列为:
X 0 1 2 3
P
则.
19.(1),(2)
【详解】解:(1)由,得,
因为在处的切线方程为,
所以,,
所以,
因为函数的图像过,
所以,所以解得,
所以,
(2)令,则
,令,即,得或,
当时,,当时,,
所以在上递增,在上递减,
因为,,
所以的最小值为
要不等式在区间上恒成立,只要在区间上恒成立,
所以只要,所以,
所以实数的取值范围为
20.(1)证明见解析;(2).
【详解】(1)取中点,连接、,
,为的中点,则, ,
平面,平面平面,平面平面,
平面,
平面,,
又,四边形是平行四边形,,
是等边三角形,,
平面,平面平面,平面平面,
平面,平面,
平面,平面平面;
(2)由(1)得平面,又平面,,
又,,
以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、,
平面的一个法向量为,
设平面的一个法向量为,,,
则,取,得,
设平面与平面所成锐二面角的平面角为,则.
因此,平面与平面所成锐二面角的余弦值为.
21.(1)
(2)存在,
(1)
圆的圆心为,半径为4,
∵线段的垂直平分线与线段交于点,∴,
因为在圆的内部,又,
∴
∴点的轨迹是以为焦点的椭圆,长轴长,半焦距,
∴,短半轴长
∴点的轨迹方程为
(2)
假设存在常数λ,使恒成立,则,
①当l1,l2中一条斜率不存在时,可知|AB|,|CD|其中一个长为2a=4,另一个为,
此时,
②当l1,l2的斜率存在且不为0时,不妨设l1:x=ty+1(t≠0),,
,
联立得
∴,,
∴,
用代替上式中的t可得,,
∴,
综上所述,存在常数使得恒成立.
22.(1)答案见解析;(2)证明见解析.
【详解】解:(1)函数的定义域为,.
①当时,则当时,恒成立
在上单调递减,无单调递增区间;
②当时,则由得
当时,;
当时,.
在上单调递减,在上单调递增,
综上所述,当时,在上单调递减,无单调递增区间;
当时,在上单调递减,在上单调递增.
(2),.
满足,
,
即
欲证,
即证,
即证,又,,即证
亦证
即
即证
设,即证.
设.
在上恒成立,
在上单调递减,
.
.
即成立
答案第1页,共2页
同课章节目录
