11.3角的平分线的性质
文档属性
| 名称 | 11.3角的平分线的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-07 00:00:00 | ||
图片预览

文档简介
课件21张PPT。11.3角的平分线的性质复习提问1、角平分线的概念 2、点到直线距离的意义。一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。 (1)工人师傅经常用角尺平分一个任意角.做法如下:
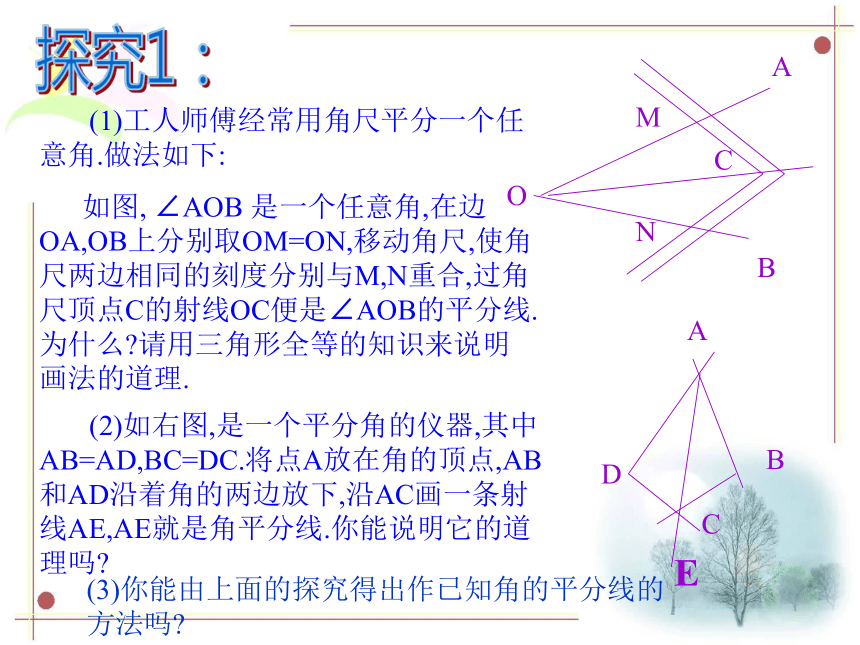
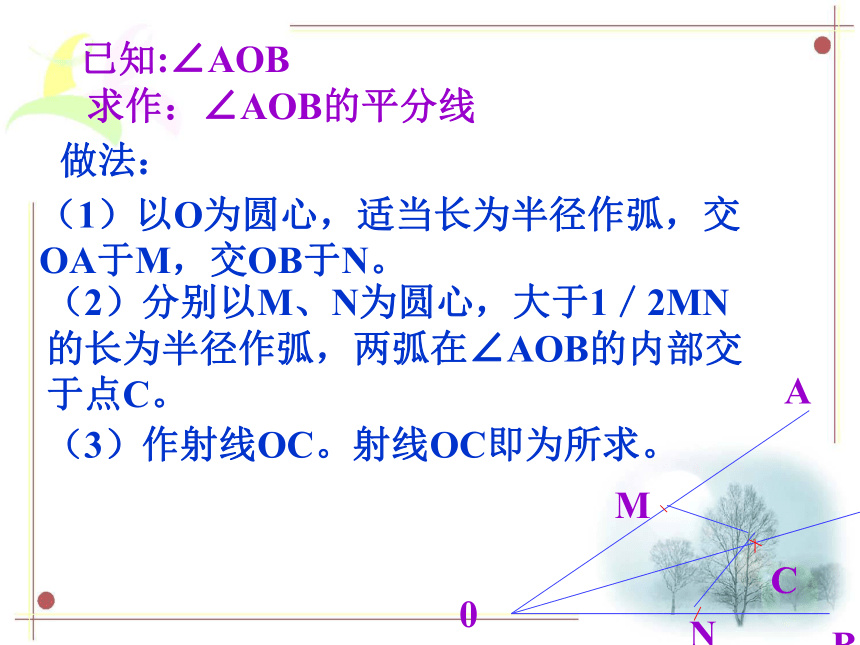
如图, ∠AOB 是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.为什么?请用三角形全等的知识来说明画法的道理. (2)如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?(3)你能由上面的探究得出作已知角的平分线的方法吗?探究1:E已知:∠AOB求作:∠AOB的平分线(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。(2)分别以M、N为圆心,大于1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。(3)作射线OC。射线OC即为所求。
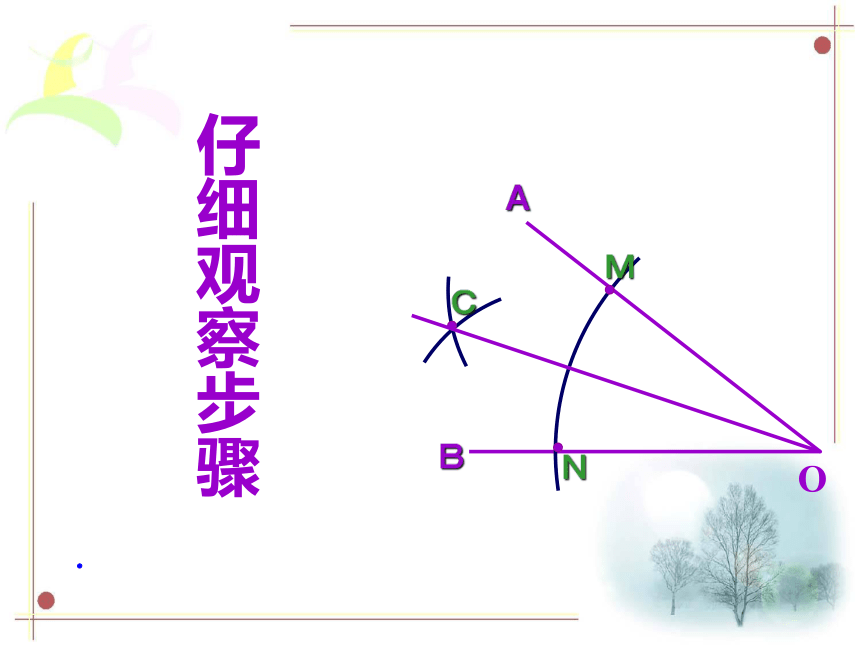
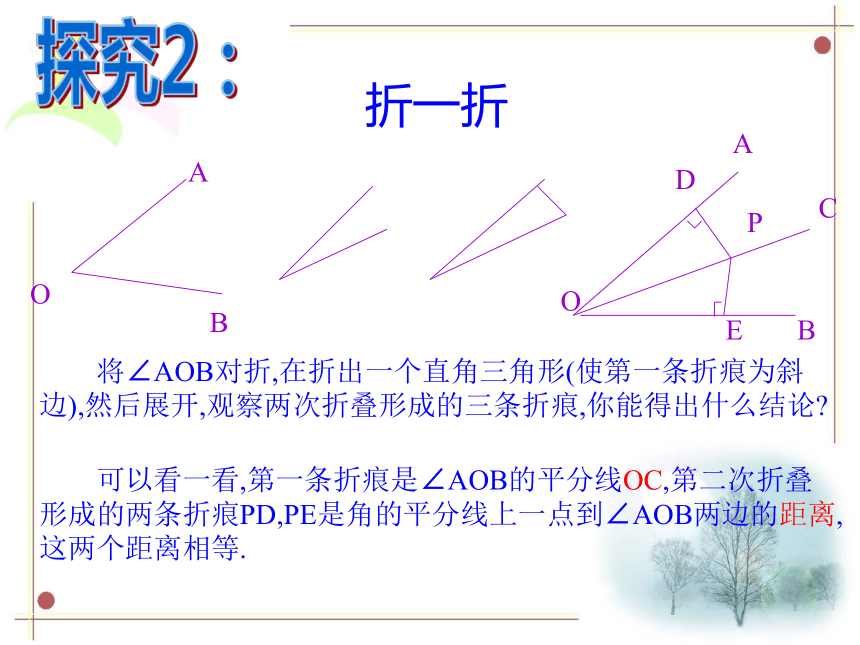
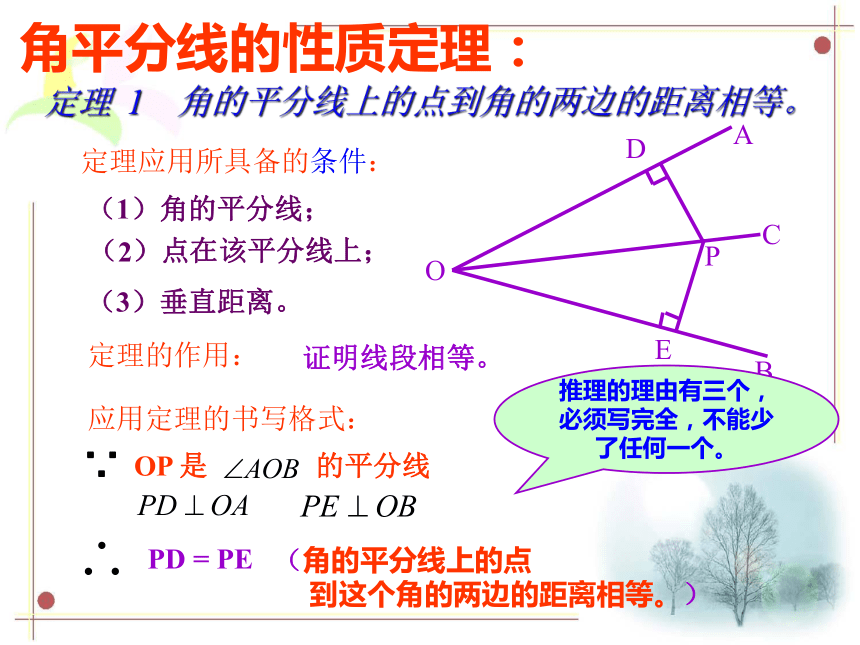
A0BMNC做法:AB.O仔细观察步骤 将∠AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论? 可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.折一折探究2:角平分线的性质定理: 定理 1 角的平分线上的点到角的两边的距离相等。定理应用所具备的条件:定理的作用: 证明线段相等。应用定理的书写格式:OP 是 的平分线PD = PE(角的平分线上的点
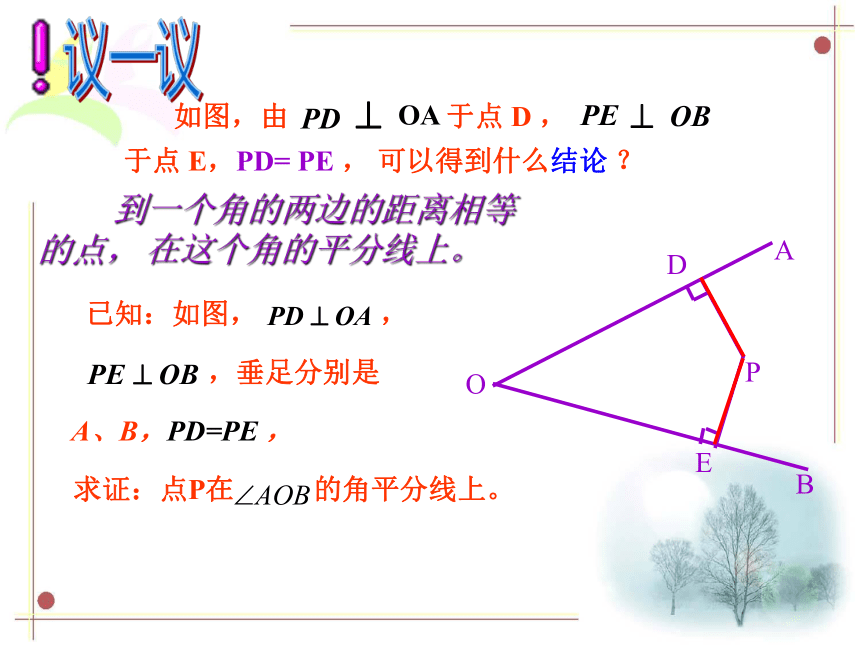
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。 如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ? 议一议 到一个角的两边的距离相等的点, 在这个角的平分线上。 已知:如图, ,
,垂足分别是
A、B,PD=PE ,
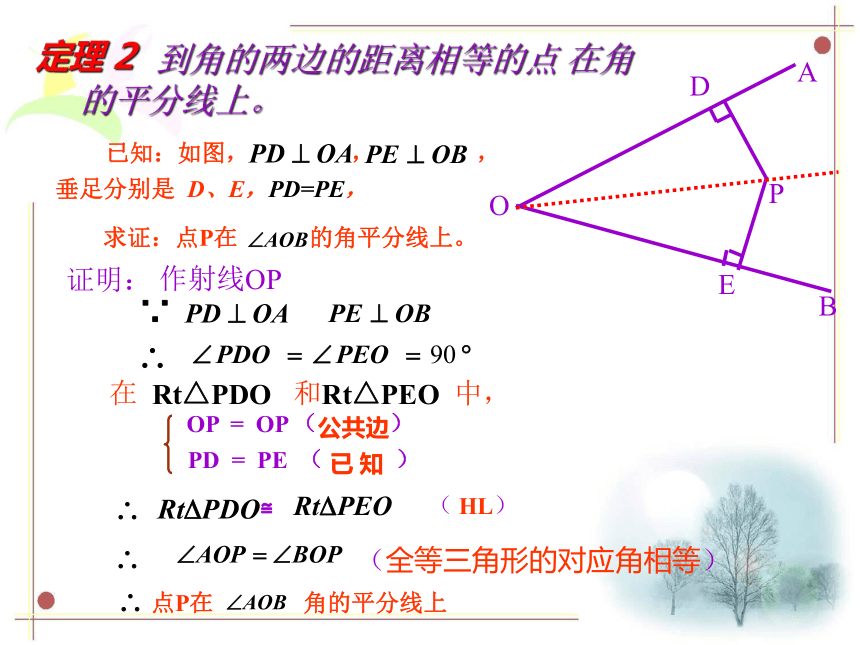
求证:点P在 的角平分线上。 到角的两边的距离相等的点 在角的平分线上。 已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。证明:作射线OP 点P在 角的平分线上 在 Rt△PDO 和Rt△PEO 中,( HL)(全等三角形的对应角相等) OP = OP (公共边)PD = PE ( 已 知 )定理 2定理 2的应用书写格式:OP 是 的平分线PD= PE (到一个角的
两边的距离相等的点, 在这个角的平分线上)
∵定理 1 在角的平分线上的点到这个角的两边的距离相等。定理 2 到一个角的两边的距离相等的点, 在这个角的平分线上。∵PD = PE用途:证线段相等用途:判定一条射线是角平分线∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)练习:∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等4、△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?ABCDE已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
例题讲解:BACPNM证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、 CA的距离相等∵BM是△ABC的角平分线,点P在BM上
∴PD=PE1 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。60BF2 如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么线段BE是△ABC的 ,AE+DE= 。
角的平分线AC随堂练习3 已知:如图,△ABC的∠B的外角的平分线BD和∠C的外角平分线CE相交于点P。
求证:点P在∠BAC的平分线上。DE应用与拓展
1.在ABC中, ∠C=900,AD平分BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为多少?
2.能用尺规作出一个450的角吗?3.已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,求证:PM=PNP(1)角平分线的性质定理及其逆定理及作用;(2)用这两个定理,一定要具备两个垂直距离(即点到直线的距离),证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样做实际是重新证了一次定理)。小结:(3)怎样找三角形内到三角形三边距离相等的点。再见!
如图, ∠AOB 是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.为什么?请用三角形全等的知识来说明画法的道理. (2)如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?(3)你能由上面的探究得出作已知角的平分线的方法吗?探究1:E已知:∠AOB求作:∠AOB的平分线(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。(2)分别以M、N为圆心,大于1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。(3)作射线OC。射线OC即为所求。
A0BMNC做法:AB.O仔细观察步骤 将∠AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论? 可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.折一折探究2:角平分线的性质定理: 定理 1 角的平分线上的点到角的两边的距离相等。定理应用所具备的条件:定理的作用: 证明线段相等。应用定理的书写格式:OP 是 的平分线PD = PE(角的平分线上的点
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。 如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ? 议一议 到一个角的两边的距离相等的点, 在这个角的平分线上。 已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。 到角的两边的距离相等的点 在角的平分线上。 已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。证明:作射线OP 点P在 角的平分线上 在 Rt△PDO 和Rt△PEO 中,( HL)(全等三角形的对应角相等) OP = OP (公共边)PD = PE ( 已 知 )定理 2定理 2的应用书写格式:OP 是 的平分线PD= PE (到一个角的
两边的距离相等的点, 在这个角的平分线上)
∵定理 1 在角的平分线上的点到这个角的两边的距离相等。定理 2 到一个角的两边的距离相等的点, 在这个角的平分线上。∵PD = PE用途:证线段相等用途:判定一条射线是角平分线∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)练习:∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等4、△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?ABCDE已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
例题讲解:BACPNM证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、 CA的距离相等∵BM是△ABC的角平分线,点P在BM上
∴PD=PE1 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。60BF2 如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么线段BE是△ABC的 ,AE+DE= 。
角的平分线AC随堂练习3 已知:如图,△ABC的∠B的外角的平分线BD和∠C的外角平分线CE相交于点P。
求证:点P在∠BAC的平分线上。DE应用与拓展
1.在ABC中, ∠C=900,AD平分BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为多少?
2.能用尺规作出一个450的角吗?3.已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,求证:PM=PNP(1)角平分线的性质定理及其逆定理及作用;(2)用这两个定理,一定要具备两个垂直距离(即点到直线的距离),证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样做实际是重新证了一次定理)。小结:(3)怎样找三角形内到三角形三边距离相等的点。再见!
