15.2.3 整数指数幂 课件(共29张PPT)人教版数学八年级上册
文档属性
| 名称 | 15.2.3 整数指数幂 课件(共29张PPT)人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 21:27:49 | ||
图片预览






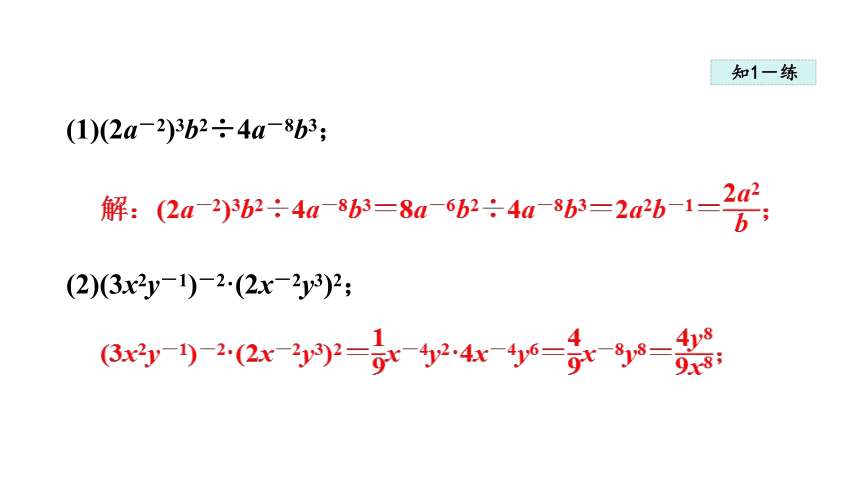
文档简介
(共29张PPT)
15.2 分式的运算
第十五章 分式
15.2.3 整数指数幂
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
整数指数幂
科学记数法
知识点
整数指数幂
知1-讲
1
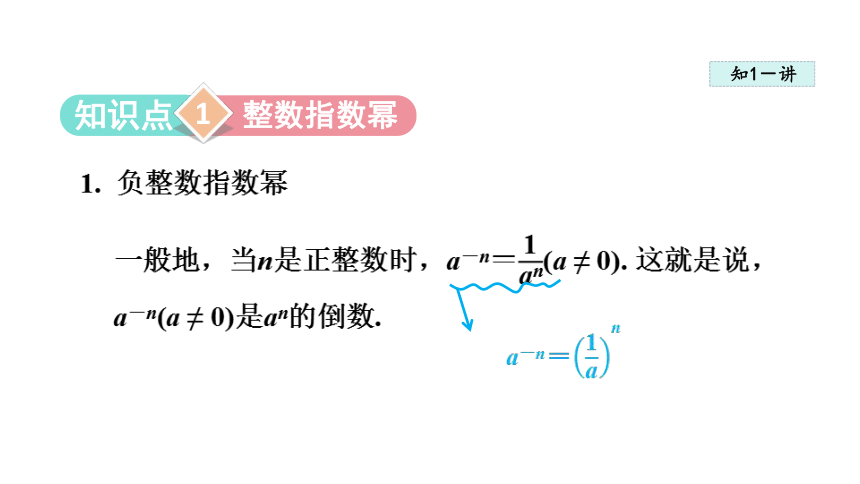
1. 负整数指数幂
一般地,当n是正整数时,a-n=(a ≠ 0). 这就是说,a-n(a ≠ 0)是an的倒数.
a-n=
知1-讲
2. 整数指数幂的运算性质
(1)am·an=am+n(a ≠ 0,m,n是整数);
(2)(am)n=amn(a ≠ 0,m,n是整数);
(3)(ab)n=anbn(a ≠ 0,b ≠ 0,n是整数);
(4)am÷an=am-n(a ≠ 0,m,n是整数);
(5)()n= (a ≠ 0,b ≠ 0,n 是整数).
此外,规定a0=1(a ≠ 0),即任何不等于0的数的0指数幂都等于1.
可化为同底数幂的乘法am·a-n=am-n
可化为积的乘方(a·b-1)n=an·b-n=
知1-讲
特别解读
1. 当指数为负整数或0时,一定要保证底数不为0.
2. 负整数指数幂的运算结果要化成正整数指数幂的形式.
知1-练
例 1
计算:+|-4|+(-1)0-=_________.
解题秘方:根据实数的运算法则进行计算.
解: +|-4|+(-1)0-=3+4+1-2=6.
6
知1-练
1-1.[中考· 连云港]计算:|-4|+(π- )0-()-1
解:原式=4+1-2=5-2=3.
知1-练
[母题 教材P144例9]计算:
(1)(2a-2)3b2÷4a-8b3;
(2)(3x2y-1)-2·(2x-2y3)2;
(3)· ÷.
解题秘方:按照先算乘方,再算乘除的顺序进行计算.
例 2
知1-练
(1)(2a-2)3b2÷4a-8b3;
(2)(3x2y-1)-2·(2x-2y3)2;
解:(2a-2)3b2÷4a-8b3=8a-6b2÷4a-8b3=2a2b-1=;
(3x2y-1)-2·(2x-2y3)2=x-4y2·4x-4y6=x-8y8=;
(3)· ÷.
知1-练
解:· ÷=x-4y2·y-6x3÷x4y-4
=x-4y2·x3y-6·x-4y4=x-5y0=.
知1-练
2-1. 利用负整数指数幂把下列各式化成分母不含字母的 式子:
(1);(2).
知1-练
2-2. 计算:
(1)(a-1b2c-3)3;
(2)a-2b3·(a2b-2)-3;
(3)(2ab2c-3)-2÷(a-2b)3.
知2-讲
知识点
科学记数法
2
1. 用科学记数法表示数 用科学记数法可以把一个大于10 的数表示成a×10n的形式(其中1 ≤ a < 10,n是正整数),引进负整数指数幂后,也可以用科学记数法把一个小于1 的正数表示为a×10-n的形式(其中1 ≤ a < 10,n是正整数).
知2-讲
2. 用科学记数法表示小于1 的正数的一般步骤
(1)确定a:a是大于或等于1 且小于10的数.
(2)确定n:确定n的方法有两种,即① n等于原数中左起第一个非0的数字前面0的个数(包括小数点前的那个0);②小数点向右移到第一个非0的数字后,小数点移动了几位,n就等于几.
(3)将原数用科学记数法表示为a×10-n的形式(其中1 ≤ a < 10,n是正整数).
知2-讲
特别解读
科学记数法是一种记数方法,不改变此数的性质和大小.用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
知2-讲
特别提醒
1.对于大于-1的负数也可以类似地用科学记数法表示成a× 10-n的形式( 其中1 ≤ |a|<10,n是正整数),也就是说可以用科学记数法表示绝对值小于1的数.
2.用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n 前面的“- ”号.
知2-练
用科学记数法表示下列各数:
(1)0.000 003;(2)-0.000 020 8;(3)0.000 000 004 67.
解题秘方:按照科学记数法的要求,将各数写成a×10-n 的形式,其中1 ≤ |a|< 10,n是正整数.
例 3
n是原数中左起第一个不
为0 的数字前面0 的个数
知2-练
解:(1)0.000 003=3×10-6;
(2)-0.000 020 8=-2.08×10-5;
(3)0.000 000 004 67=4.67×10-9.
知2-练
3-1.[中考· 眉山] 生物学家发现了某种花粉的直径约为0.000 002 1毫米,数据0.000 002 1用科学记数法表示正确的是( )
A.2.1×10-6
B.21×10-6
C.2.1×10-5
D.21×10-5
A
知2-练
3-2 . [新趋势 学科综合]“ 墙角数枝梅, 凌寒独自开.遥知不是雪,为有暗香来.” 出自宋代诗人王安石的《梅花》. 梅花的花粉直径约为0.000 036 m,用科学记数法表示该数据为 ___________.
6×10-5
知2-练
将下列用科学记数法表示的数还原成原数.
(1)6×10-4;
(2)-7.2×10-5;
(3)5.68×10-6.
解题秘方:把用科学记数法表示的绝对值小于1 的数还原时,指数的绝对值是几,小数点就向左移动几位.
例 4
解:6×10-4=0.000 6;
-7.2×10-5=-0.000 072;
5.68×10-6=0.000 005 68.
知2-练
教你一招:把用科学记数法表示的绝对值小于1 的数还原的思路:把a×10-n(其中1 ≤|a|< 10,n是正整数)还原成原数时,只要把a的小数点向左移动n 位即可.
知2-练
4-1.[中考·德阳] 把实数6.12×10-3 用小数表示为( )
A.0.061 2
B.6 120
C.0.006 12
D.612 000
C
知2-练
4-2. 把下列用科学记数法表示的数还原:
(1)7.2×10-5;
(2)-1.5×10-4.
解:7.2×10-5=0.000 072;
-1.5×10-4=-0.000 15.
知2-练
[母题 教材P146练习T2]计算:
(1)(3×10-4)2×(2×10-6)3;
(2)(8×10-7)2÷(2×10-3)3.
解题秘方:先计算乘方,再计算乘除.
例 5
知2-练
(1)(3×10-4)2×(2×10-6)3;
解:(3×10-4)2×(2×10-6)3
=9×10-8×8×10-18
=(9×8)×(10-8×10-18)
=72×10-26
=7.2×10-25;
知2-练
(2)(8×10-7)2÷(2×10-3)3.
解:(8×10-7)2÷(2×10-3)3
=(64×10-14)÷(8×10-9)
=(64÷8)×(10-14÷10-9)
=8×10-5.
知2-练
5-1. 计算(结果用科学记数法表示):
(1)(2×107)×(8×10-9);
(2)(5.2×10-9)÷(-4×103).
解:原式=16×10-2=1.6×10-1;
原式=-1.3×10-12.
整数指数幂
整数
指数幂
科学记数法
正整数指数幂
0 指数幂
负整数指数幂
15.2 分式的运算
第十五章 分式
15.2.3 整数指数幂
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
整数指数幂
科学记数法
知识点
整数指数幂
知1-讲
1
1. 负整数指数幂
一般地,当n是正整数时,a-n=(a ≠ 0). 这就是说,a-n(a ≠ 0)是an的倒数.
a-n=
知1-讲
2. 整数指数幂的运算性质
(1)am·an=am+n(a ≠ 0,m,n是整数);
(2)(am)n=amn(a ≠ 0,m,n是整数);
(3)(ab)n=anbn(a ≠ 0,b ≠ 0,n是整数);
(4)am÷an=am-n(a ≠ 0,m,n是整数);
(5)()n= (a ≠ 0,b ≠ 0,n 是整数).
此外,规定a0=1(a ≠ 0),即任何不等于0的数的0指数幂都等于1.
可化为同底数幂的乘法am·a-n=am-n
可化为积的乘方(a·b-1)n=an·b-n=
知1-讲
特别解读
1. 当指数为负整数或0时,一定要保证底数不为0.
2. 负整数指数幂的运算结果要化成正整数指数幂的形式.
知1-练
例 1
计算:+|-4|+(-1)0-=_________.
解题秘方:根据实数的运算法则进行计算.
解: +|-4|+(-1)0-=3+4+1-2=6.
6
知1-练
1-1.[中考· 连云港]计算:|-4|+(π- )0-()-1
解:原式=4+1-2=5-2=3.
知1-练
[母题 教材P144例9]计算:
(1)(2a-2)3b2÷4a-8b3;
(2)(3x2y-1)-2·(2x-2y3)2;
(3)· ÷.
解题秘方:按照先算乘方,再算乘除的顺序进行计算.
例 2
知1-练
(1)(2a-2)3b2÷4a-8b3;
(2)(3x2y-1)-2·(2x-2y3)2;
解:(2a-2)3b2÷4a-8b3=8a-6b2÷4a-8b3=2a2b-1=;
(3x2y-1)-2·(2x-2y3)2=x-4y2·4x-4y6=x-8y8=;
(3)· ÷.
知1-练
解:· ÷=x-4y2·y-6x3÷x4y-4
=x-4y2·x3y-6·x-4y4=x-5y0=.
知1-练
2-1. 利用负整数指数幂把下列各式化成分母不含字母的 式子:
(1);(2).
知1-练
2-2. 计算:
(1)(a-1b2c-3)3;
(2)a-2b3·(a2b-2)-3;
(3)(2ab2c-3)-2÷(a-2b)3.
知2-讲
知识点
科学记数法
2
1. 用科学记数法表示数 用科学记数法可以把一个大于10 的数表示成a×10n的形式(其中1 ≤ a < 10,n是正整数),引进负整数指数幂后,也可以用科学记数法把一个小于1 的正数表示为a×10-n的形式(其中1 ≤ a < 10,n是正整数).
知2-讲
2. 用科学记数法表示小于1 的正数的一般步骤
(1)确定a:a是大于或等于1 且小于10的数.
(2)确定n:确定n的方法有两种,即① n等于原数中左起第一个非0的数字前面0的个数(包括小数点前的那个0);②小数点向右移到第一个非0的数字后,小数点移动了几位,n就等于几.
(3)将原数用科学记数法表示为a×10-n的形式(其中1 ≤ a < 10,n是正整数).
知2-讲
特别解读
科学记数法是一种记数方法,不改变此数的性质和大小.用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
知2-讲
特别提醒
1.对于大于-1的负数也可以类似地用科学记数法表示成a× 10-n的形式( 其中1 ≤ |a|<10,n是正整数),也就是说可以用科学记数法表示绝对值小于1的数.
2.用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n 前面的“- ”号.
知2-练
用科学记数法表示下列各数:
(1)0.000 003;(2)-0.000 020 8;(3)0.000 000 004 67.
解题秘方:按照科学记数法的要求,将各数写成a×10-n 的形式,其中1 ≤ |a|< 10,n是正整数.
例 3
n是原数中左起第一个不
为0 的数字前面0 的个数
知2-练
解:(1)0.000 003=3×10-6;
(2)-0.000 020 8=-2.08×10-5;
(3)0.000 000 004 67=4.67×10-9.
知2-练
3-1.[中考· 眉山] 生物学家发现了某种花粉的直径约为0.000 002 1毫米,数据0.000 002 1用科学记数法表示正确的是( )
A.2.1×10-6
B.21×10-6
C.2.1×10-5
D.21×10-5
A
知2-练
3-2 . [新趋势 学科综合]“ 墙角数枝梅, 凌寒独自开.遥知不是雪,为有暗香来.” 出自宋代诗人王安石的《梅花》. 梅花的花粉直径约为0.000 036 m,用科学记数法表示该数据为 ___________.
6×10-5
知2-练
将下列用科学记数法表示的数还原成原数.
(1)6×10-4;
(2)-7.2×10-5;
(3)5.68×10-6.
解题秘方:把用科学记数法表示的绝对值小于1 的数还原时,指数的绝对值是几,小数点就向左移动几位.
例 4
解:6×10-4=0.000 6;
-7.2×10-5=-0.000 072;
5.68×10-6=0.000 005 68.
知2-练
教你一招:把用科学记数法表示的绝对值小于1 的数还原的思路:把a×10-n(其中1 ≤|a|< 10,n是正整数)还原成原数时,只要把a的小数点向左移动n 位即可.
知2-练
4-1.[中考·德阳] 把实数6.12×10-3 用小数表示为( )
A.0.061 2
B.6 120
C.0.006 12
D.612 000
C
知2-练
4-2. 把下列用科学记数法表示的数还原:
(1)7.2×10-5;
(2)-1.5×10-4.
解:7.2×10-5=0.000 072;
-1.5×10-4=-0.000 15.
知2-练
[母题 教材P146练习T2]计算:
(1)(3×10-4)2×(2×10-6)3;
(2)(8×10-7)2÷(2×10-3)3.
解题秘方:先计算乘方,再计算乘除.
例 5
知2-练
(1)(3×10-4)2×(2×10-6)3;
解:(3×10-4)2×(2×10-6)3
=9×10-8×8×10-18
=(9×8)×(10-8×10-18)
=72×10-26
=7.2×10-25;
知2-练
(2)(8×10-7)2÷(2×10-3)3.
解:(8×10-7)2÷(2×10-3)3
=(64×10-14)÷(8×10-9)
=(64÷8)×(10-14÷10-9)
=8×10-5.
知2-练
5-1. 计算(结果用科学记数法表示):
(1)(2×107)×(8×10-9);
(2)(5.2×10-9)÷(-4×103).
解:原式=16×10-2=1.6×10-1;
原式=-1.3×10-12.
整数指数幂
整数
指数幂
科学记数法
正整数指数幂
0 指数幂
负整数指数幂
