15.3 分式方程 课件(共42张PPT)人教版数学八年级上册
文档属性
| 名称 | 15.3 分式方程 课件(共42张PPT)人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
15.3 分式方程
第十五章 分式
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
分式方程的概念
分式方程的解法
分式方程的应用
知识点
分式方程的概念
知1-讲
1
1. 分式方程
分母中含有未知数的方程叫做分式方程.
分母中是否含有未知数是区分分式方程和整式方程的依据.
知1-讲
2. 判断一个方程是分式方程的条件
(1)是方程;
(2)含有分母;
(3)分母中含有未知数.
以上三者缺一不可.
特别提醒
1. 识别分式方程时,不能对方程进行约分或通分变形,更不能用等式的性质变形.
2.分母中有字母,但字母不是未知数的方程也不是分式方程.
知1-练
例 1
判断下列方程是不是分式方程,并说明理由.
(1)=8; (2)=;(3)=1;
(4)=;(5)-2=x(a为非零常数).
解题秘方:利用判别分式方程的依据——分母中含有未知数进行识别.
知1-练
解:(1)不是分式方程,因为分母中不含有未知数.
(2)是分式方程,因为分母中含有未知数.
(3)是分式方程,因为分母中含有未知数.
(4)是分式方程,因为分母中含有未知数.
(5)不是分式方程,因为分母中虽然含有字母a,但a为
非零常数,不是未知数.
知1-练
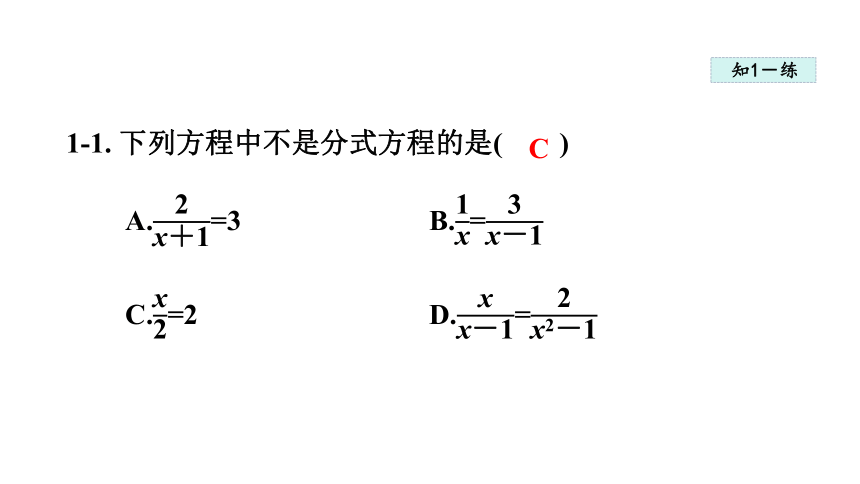
1-1. 下列方程中不是分式方程的是( )
A.=3 B.=
C.=2 D.=
C
知1-练
1-2. 下列关于x的方程:
①x2=1;②-x2=1;
③=x;④+3=;
其中是分式方程的是________(填序号).
③④
知2-讲
知识点
分式方程的解法
2
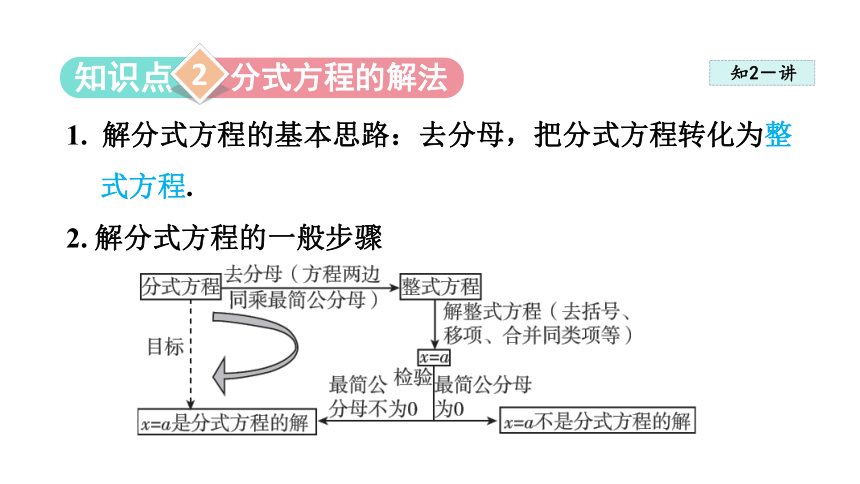
1. 解分式方程的基本思路:去分母,把分式方程转化为整式方程.
2. 解分式方程的一般步骤
知2-讲
3. 检验分式方程解的方法
(1)直接检验法:将整式方程的解代入原分式方程,这种方法不仅能检验出该解是否适合原分式方程,还能检验所得的解是否正确.
(2)公分母检验法:将整式方程的解代入最简公分母,若最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
方法比较简单,计算量小,因此被广泛运用
知2-讲
4. 增根 在分式方程化为整式方程的过程中,若整式方程的解使最简公分母的值为0, 则这个解叫做原分式方程的增根.
知2-讲
特别解读
1. 解分式方程的关键是去分母. 去分母时不要漏乘不含分母的项,当分子是多项式时要用括号括起来.
2. 解分式方程一定要检验,对于增根必须舍去.
3. 对增根的理解:
(1) 增根一定是分式方程化为的整式方程的解;
(2)若分式方程有增根,则必是使最简公分母为0 时未知数的值.
知2-讲
4. 一般情况下,解关于哪个字母的分式方程,则哪个字母表示未知数,其余字母都作为常数存在.
知2-练
解下列方程:
(1)=;(2)=-2;
(3)-=1;(4)+=.
例 2
解题秘方:将分式方程转化为整式方程,通过求整式方程的解并检验,从而得到分式方程的解.
知2-练
解:方程两边乘(x-4)(x-6),
得x(x-6)=(x+2)(x-4). 解得x=2.
检验:当x=2 时,(x-4)(x-6)≠ 0.
∴原分式方程的解为x=2.
(1)=;
知2-练
解:方程两边乘(x-3),得2-x=-1-2(x-3).
解得x=3.
检验:当x=3 时,x-3=0,
因此 x=3不是原分式方程的解.
所以原分式方程无解.
(2)=-2;
知2-练
解:方程两边乘3(x-1),
得4x+6-3(5x-4)=3(x-1). 解得x=.
检验:当x=时,3(x-1)≠ 0.
∴原分式方程的解为x=.
(3)-=1;
知2-练
解:原方程可化为+= .
方程两边乘x(x+2)(x-2),
得4(x-2)+7x=6(x+2).解得x=4.
检验:当x=4 时,x(x+2)(x-2)≠ 0.
∴原分式方程的解为x=4.
(4)+=.
知2-练
2-1.[中考·株洲] 将关于x 的分式方程=去分母可得( )
A.3x-3=2x B.3x-1=2x
C.3x-1=x D.3x-3=x
A
知2-练
2-2.[中考·苏州] 分式方程=的解为x=_____ .
-3
知2-练
2-3.[中考·连云港]解方程:=-3.
解:方程两边乘x-2,得2x-5=3x-3-3(x-2),解得x=4.
检验:当x=4时,x-2≠0.
所以原分式方程的解为x=4.
知3-讲
知识点
分式方程的应用
3
1. 列分式方程常用的等量关系
(1)行程问题:速度× 时间=路程.
(2)利润问题:利润= 售价-进价;利润率=利润÷进价×100%.
(3)工程问题:工作量=工作时间× 工作效率;总工作量=各个分工作量之和.
(4)储蓄问题:本息和= 本金+ 利息.
知3-讲
2. 列分式方程解应用题的一般步骤
(1)审:即审题, 根据题意找出已知量和未知量,并找出等量关系.
(2)设:即设未知数,设未知数的方法有直接设和间接设,注意单位要统一,选择一个未知量用未知数表示,并用含未知数的式子表示相关量.
(3)列:即列方程,根据等量关系列出分式方程.
(4)解:即解所列的分式方程,求出未知数的值.
(5)验:即验根,既要检验所求的未知数的值是否适合分式方程,还要检验此解是否符合实际意义.
(6)答:即写出答案,注意单位和答案要完整.
知3-讲
特别解读
1. 审题时,先寻找题目中的关键词,然后借助列表、画图等方法准确找出等量关系.当题目中包含多个等量关系时,要选择一个能够体现全部(或大部分)数量的等量关系列方程.
2. 设未知数时,一般题中问什么就设什么,即设直接未知数;若设直接未知数难以列方程,则可设另一个相关量为未知数,即设间接未知数;有时设一个未知数无法表示出等量关系,可设多个未知数,即设辅助未知数.
3. 应用题中解分式方程同样要验根.
知3-练
[母题中考· 威海教材P154练习T1]某校组织学生去郭永怀纪念馆进行研学活动.纪念馆距学校72 km,一部分学生乘坐大型客车先行,出发12 min 后,另一部分学生乘坐小型客车前往,结果同时到达.已知小型客车的速度是大型客车速度的1.2 倍,求大型客车的速度.
例 3
知3-练
思路引导:
知3-练
解:设大型客车的速度为x km/h,
则小型客车的速度为1.2x km/h,12 min= h.
根据题意,得-= ,解得x = 6 0.
经检验,x = 6 0 是方程的解.
答:大型客车的速度是60 km/h.
知3-练
3-1.[中考· 广州] 随着城际交通的快速发展, 某次动车平均提速60 km/h, 动车提速后行驶480 km 与提速前行驶360 km 所用的时间相同. 设动车提速后的平均速度为x km/h, 则下列方程正确的是( )
A.= B.=
C.= D.=
B
知3-练
[中考·随州] 某市区一条主要街道的改造工程有甲、乙两个工程队投标.经测算:若由两个工程队合作,12 天恰好完成;若两个队合作9 天后,剩下的由甲队单独完成,还需5 天时间,现需从这两个工程队中选出一个队单独完成,从缩短工期角度考虑,你认为应该选择哪个队?为什么?
例 4
知3-练
思路引导:
工作效率 工作时间/天 工作总量
甲乙合作 9
甲 5
等量关系 系甲乙合作9 天的工程量+ 甲单独工作5 天的工程量=1
知3-练
解:设甲队单独完成工程需x 天.
根据题意,得×9 +×5=1,解得x =20 .
经检验,x =20 是方程的解.
因为-= ,所以乙单独完成工程需30 天.
又因为20 天<3 0 天,
所以从缩短工期角度考虑,应该选择甲队.
知3-练
4-1.“ 畅通交通, 扮靓城市”, 某市在道路提升改造中, 将一座长度为36 m 的桥梁进行重新改造. 为了尽快通车, 某施工队在实际施工时, 每天工作效率比原计划提高了50%,结果提前2天成功地完成了大桥的改造任务, 那么该施工队原计划每天改造多少米?
知3-练
知3-练
[情境题 校园文化]为了进一步丰富校园文体活动,某中学准备一次性购买若干个足球和排球,用480 元购买足球的数量和用390 元购买排球的数量相同,已知足球的单价比排球的单价多15 元.
例 5
知3-练
思路导引:
(1)足球和排球的单价各是多少元?
知3-练
解:设足球的单价是x 元,则排球的单价是(x-15)元.
根据题意,得= ,解得x =80 .
经检验,x =80 是方程的解,且符合题意.
∴ x-15 = 6 5.
答:足球的单价是80 元,排球的单价是65 元.
知3-练
思路导引:
(2)根据学校实际情况,需一次性购买足球和排球共100 个,但要求其总费用不超过7 550 元,那么学校最多可以购买多少个足球?
知3-练
解:设学校可以购买m 个足球,
则可以购买(100 -m)个排球.
根据题意,得80m+65(100 -m)≤ 755 0,
解得m ≤ 70.
又∵ m 为正整数,∴ m 可以取的最大值为70.
答:学校最多可以购买70 个足球.
知3-练
5-1.[中考· 永州] 某水果店搞促销活动,对某种水果打8 折出售,若用60 元钱买这种水果, 可以比打折前多买3 千克. 设该种水果打折前的单价为x元, 根据题意可列方程为 _________________.
知3-练
5-2. 某校篮球社团人数迅增,急需购进A,B 两种品牌篮球, 已知A 品牌篮球的单价比B 品牌篮球单价的2 倍少48 元,采购相同数量的A,B 两种品牌篮球分别需要花费9 600 元和7 200 元.A,B 两种品牌篮球的单价分别是多少元?
知3-练
分式方程
分
式
方
程
分式方程
的应用
列
解法
增根
产
生
15.3 分式方程
第十五章 分式
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
分式方程的概念
分式方程的解法
分式方程的应用
知识点
分式方程的概念
知1-讲
1
1. 分式方程
分母中含有未知数的方程叫做分式方程.
分母中是否含有未知数是区分分式方程和整式方程的依据.
知1-讲
2. 判断一个方程是分式方程的条件
(1)是方程;
(2)含有分母;
(3)分母中含有未知数.
以上三者缺一不可.
特别提醒
1. 识别分式方程时,不能对方程进行约分或通分变形,更不能用等式的性质变形.
2.分母中有字母,但字母不是未知数的方程也不是分式方程.
知1-练
例 1
判断下列方程是不是分式方程,并说明理由.
(1)=8; (2)=;(3)=1;
(4)=;(5)-2=x(a为非零常数).
解题秘方:利用判别分式方程的依据——分母中含有未知数进行识别.
知1-练
解:(1)不是分式方程,因为分母中不含有未知数.
(2)是分式方程,因为分母中含有未知数.
(3)是分式方程,因为分母中含有未知数.
(4)是分式方程,因为分母中含有未知数.
(5)不是分式方程,因为分母中虽然含有字母a,但a为
非零常数,不是未知数.
知1-练
1-1. 下列方程中不是分式方程的是( )
A.=3 B.=
C.=2 D.=
C
知1-练
1-2. 下列关于x的方程:
①x2=1;②-x2=1;
③=x;④+3=;
其中是分式方程的是________(填序号).
③④
知2-讲
知识点
分式方程的解法
2
1. 解分式方程的基本思路:去分母,把分式方程转化为整式方程.
2. 解分式方程的一般步骤
知2-讲
3. 检验分式方程解的方法
(1)直接检验法:将整式方程的解代入原分式方程,这种方法不仅能检验出该解是否适合原分式方程,还能检验所得的解是否正确.
(2)公分母检验法:将整式方程的解代入最简公分母,若最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
方法比较简单,计算量小,因此被广泛运用
知2-讲
4. 增根 在分式方程化为整式方程的过程中,若整式方程的解使最简公分母的值为0, 则这个解叫做原分式方程的增根.
知2-讲
特别解读
1. 解分式方程的关键是去分母. 去分母时不要漏乘不含分母的项,当分子是多项式时要用括号括起来.
2. 解分式方程一定要检验,对于增根必须舍去.
3. 对增根的理解:
(1) 增根一定是分式方程化为的整式方程的解;
(2)若分式方程有增根,则必是使最简公分母为0 时未知数的值.
知2-讲
4. 一般情况下,解关于哪个字母的分式方程,则哪个字母表示未知数,其余字母都作为常数存在.
知2-练
解下列方程:
(1)=;(2)=-2;
(3)-=1;(4)+=.
例 2
解题秘方:将分式方程转化为整式方程,通过求整式方程的解并检验,从而得到分式方程的解.
知2-练
解:方程两边乘(x-4)(x-6),
得x(x-6)=(x+2)(x-4). 解得x=2.
检验:当x=2 时,(x-4)(x-6)≠ 0.
∴原分式方程的解为x=2.
(1)=;
知2-练
解:方程两边乘(x-3),得2-x=-1-2(x-3).
解得x=3.
检验:当x=3 时,x-3=0,
因此 x=3不是原分式方程的解.
所以原分式方程无解.
(2)=-2;
知2-练
解:方程两边乘3(x-1),
得4x+6-3(5x-4)=3(x-1). 解得x=.
检验:当x=时,3(x-1)≠ 0.
∴原分式方程的解为x=.
(3)-=1;
知2-练
解:原方程可化为+= .
方程两边乘x(x+2)(x-2),
得4(x-2)+7x=6(x+2).解得x=4.
检验:当x=4 时,x(x+2)(x-2)≠ 0.
∴原分式方程的解为x=4.
(4)+=.
知2-练
2-1.[中考·株洲] 将关于x 的分式方程=去分母可得( )
A.3x-3=2x B.3x-1=2x
C.3x-1=x D.3x-3=x
A
知2-练
2-2.[中考·苏州] 分式方程=的解为x=_____ .
-3
知2-练
2-3.[中考·连云港]解方程:=-3.
解:方程两边乘x-2,得2x-5=3x-3-3(x-2),解得x=4.
检验:当x=4时,x-2≠0.
所以原分式方程的解为x=4.
知3-讲
知识点
分式方程的应用
3
1. 列分式方程常用的等量关系
(1)行程问题:速度× 时间=路程.
(2)利润问题:利润= 售价-进价;利润率=利润÷进价×100%.
(3)工程问题:工作量=工作时间× 工作效率;总工作量=各个分工作量之和.
(4)储蓄问题:本息和= 本金+ 利息.
知3-讲
2. 列分式方程解应用题的一般步骤
(1)审:即审题, 根据题意找出已知量和未知量,并找出等量关系.
(2)设:即设未知数,设未知数的方法有直接设和间接设,注意单位要统一,选择一个未知量用未知数表示,并用含未知数的式子表示相关量.
(3)列:即列方程,根据等量关系列出分式方程.
(4)解:即解所列的分式方程,求出未知数的值.
(5)验:即验根,既要检验所求的未知数的值是否适合分式方程,还要检验此解是否符合实际意义.
(6)答:即写出答案,注意单位和答案要完整.
知3-讲
特别解读
1. 审题时,先寻找题目中的关键词,然后借助列表、画图等方法准确找出等量关系.当题目中包含多个等量关系时,要选择一个能够体现全部(或大部分)数量的等量关系列方程.
2. 设未知数时,一般题中问什么就设什么,即设直接未知数;若设直接未知数难以列方程,则可设另一个相关量为未知数,即设间接未知数;有时设一个未知数无法表示出等量关系,可设多个未知数,即设辅助未知数.
3. 应用题中解分式方程同样要验根.
知3-练
[母题中考· 威海教材P154练习T1]某校组织学生去郭永怀纪念馆进行研学活动.纪念馆距学校72 km,一部分学生乘坐大型客车先行,出发12 min 后,另一部分学生乘坐小型客车前往,结果同时到达.已知小型客车的速度是大型客车速度的1.2 倍,求大型客车的速度.
例 3
知3-练
思路引导:
知3-练
解:设大型客车的速度为x km/h,
则小型客车的速度为1.2x km/h,12 min= h.
根据题意,得-= ,解得x = 6 0.
经检验,x = 6 0 是方程的解.
答:大型客车的速度是60 km/h.
知3-练
3-1.[中考· 广州] 随着城际交通的快速发展, 某次动车平均提速60 km/h, 动车提速后行驶480 km 与提速前行驶360 km 所用的时间相同. 设动车提速后的平均速度为x km/h, 则下列方程正确的是( )
A.= B.=
C.= D.=
B
知3-练
[中考·随州] 某市区一条主要街道的改造工程有甲、乙两个工程队投标.经测算:若由两个工程队合作,12 天恰好完成;若两个队合作9 天后,剩下的由甲队单独完成,还需5 天时间,现需从这两个工程队中选出一个队单独完成,从缩短工期角度考虑,你认为应该选择哪个队?为什么?
例 4
知3-练
思路引导:
工作效率 工作时间/天 工作总量
甲乙合作 9
甲 5
等量关系 系甲乙合作9 天的工程量+ 甲单独工作5 天的工程量=1
知3-练
解:设甲队单独完成工程需x 天.
根据题意,得×9 +×5=1,解得x =20 .
经检验,x =20 是方程的解.
因为-= ,所以乙单独完成工程需30 天.
又因为20 天<3 0 天,
所以从缩短工期角度考虑,应该选择甲队.
知3-练
4-1.“ 畅通交通, 扮靓城市”, 某市在道路提升改造中, 将一座长度为36 m 的桥梁进行重新改造. 为了尽快通车, 某施工队在实际施工时, 每天工作效率比原计划提高了50%,结果提前2天成功地完成了大桥的改造任务, 那么该施工队原计划每天改造多少米?
知3-练
知3-练
[情境题 校园文化]为了进一步丰富校园文体活动,某中学准备一次性购买若干个足球和排球,用480 元购买足球的数量和用390 元购买排球的数量相同,已知足球的单价比排球的单价多15 元.
例 5
知3-练
思路导引:
(1)足球和排球的单价各是多少元?
知3-练
解:设足球的单价是x 元,则排球的单价是(x-15)元.
根据题意,得= ,解得x =80 .
经检验,x =80 是方程的解,且符合题意.
∴ x-15 = 6 5.
答:足球的单价是80 元,排球的单价是65 元.
知3-练
思路导引:
(2)根据学校实际情况,需一次性购买足球和排球共100 个,但要求其总费用不超过7 550 元,那么学校最多可以购买多少个足球?
知3-练
解:设学校可以购买m 个足球,
则可以购买(100 -m)个排球.
根据题意,得80m+65(100 -m)≤ 755 0,
解得m ≤ 70.
又∵ m 为正整数,∴ m 可以取的最大值为70.
答:学校最多可以购买70 个足球.
知3-练
5-1.[中考· 永州] 某水果店搞促销活动,对某种水果打8 折出售,若用60 元钱买这种水果, 可以比打折前多买3 千克. 设该种水果打折前的单价为x元, 根据题意可列方程为 _________________.
知3-练
5-2. 某校篮球社团人数迅增,急需购进A,B 两种品牌篮球, 已知A 品牌篮球的单价比B 品牌篮球单价的2 倍少48 元,采购相同数量的A,B 两种品牌篮球分别需要花费9 600 元和7 200 元.A,B 两种品牌篮球的单价分别是多少元?
知3-练
分式方程
分
式
方
程
分式方程
的应用
列
解法
增根
产
生
