北京市延庆区2023-2024学年高二下学期期末考试数学试题(图片版,含答案)
文档属性
| 名称 | 北京市延庆区2023-2024学年高二下学期期末考试数学试题(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 550.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 00:16:12 | ||
图片预览




文档简介
2024北京延庆高二(下)期末
数 学
2024.07
本试卷共 6 页,150 分。考试时长 120 分钟。考生务必将答案答在答题纸上,在试卷上作答无效。考
试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共 40 分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
x
(1)函数 y = 2 在 x = 1处的导数值为
1
(A) 2ln 2 (B)
ln 2
(C)1 (D) 2
(2)函数 3y = x + 2 在区间 [1, 2]上的平均变化率为
(A) 3 (B) 5
(C) 7 (D) 9
(3)已知数列 an 满足 an+1 = 2an , a2 = 4 ,则数列 an 的前 4 项和等于
(A)16 (B) 24
(C) 30 (D) 62
1
( )在 ( x )64 的展开式中,常数项为
x
(A) 15 (B)15
(C)30 (D)360
(5)用 0,1,2,3,4 可以组成无重复数字的两位数的个数为
(A) 20 (B) 25
(C)15 (D)16
(6)曲线 y = cos x在 x = 0 处的切线方程为
(A) y = 0 (B) y = 1
(C) y = x (D) y =1
第1页/共11页
3 2
(7)已知函数 f (x) = x + ax + x +1(a R) 有两个极值点 x1 , x2 (x1 x2 ) ,则
(A) a 3 或 a 3 (B) x 是 f (x)1 的极小值点
1 1
(C) x1 + x2 = (D) x1x2 =
3 3
(8)设 a1,a2 ,a3 , a6 是1,2,3, ,6 的一个排列. 且满足 | a1 a2 |≥| a2 a3 |≥ ≥| a5 a6 | ,
则 | a1 a2 | + | a2 a3 | + + | a5 a6 | 的最大值是
(A)17 (B)15
(C)13 (D)11
(9)设{a }是公比为 q(q 1)的无穷等比数列, Sn 为其前 n项和, a1 0 . 则“ q 0n ”
是“ Sn 存在最小值”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(10)已知数列 an 满足, n
*
N , a4n 3 = 1, a4n 1 =1, a2n = an ,该数列的前 n 项
和为 Sn ,则下列论断中错.误.的是
(A) a31 =1 (B) a2024 = 1
(C) 非零常数T ,使得 an+T = an (D) n
*
N ,都有 S n = 2 2
第二部分 (非选择题 共 110 分)
二、填空题共 5 小题,每小题 5 分,共 25 分。
(11)2023 年起延庆区将利用三年时间重点打造“延庆东南山·九沟十八湾”乡村振兴品牌,旨在借助延
庆区东南部浅山区和山区的沟域空间结构、功能布局及秀美山水,构建 9 条各具特色的生态沟域廊
道、18 条生态沟域农文体康旅体验湾,全面推动延庆区乡村振兴,打造新时代首都生态沟域绿色发
展新典范. 小明打算从九沟十八湾中选出一沟一湾去旅游,则不同的选法有_________种.
(12)已知函数 f (x) = log x (a 0且a 1)a ,若 f (1) = 1,则 a = _________.
1
( 313)已知函数 f (x) = x 4x + 4 ,则 f (x) 在区间[ 3, 3] 上的最大值为_________.
3
(14)已知数列 an 是各项均为正数的等比数列, Sn 为其前 n项和, a1a3 =16 , S3 =14,
则 a2 = _________;记Tn = a1a2 an (n =1,2, ) ,若存在 n0
*
N 使得Tn 最大,
则 n0 的值为_________.
( )已知数列{ a }的各项均为正数,满足 a = ca 215 n n+1 n + an ,其中常数 c R . 给出下列四个判断:
第2页/共11页
1
①若 a1 =1, c 0 ,则 an (n 2);
n +1
1
②若 c = 1,则 an (n 2);
n +1
③若 c =1, an n (n 2),则 a1 1;
④ a1 =1,不存在实数 c ,使得 an n (n 2).
其中所有正确判断的序号是_________.
三、解答题共 6 小题,共 85 分。解答应写出文字说明,证明过程或演算步骤。
(16)(本小题 14 分)
求下列函数的导函数.
(Ⅰ) 2 x
log x
f (x) = x e ; (Ⅱ) f (x) = 2 ;
2x
sin x
(Ⅲ) f (x) = ; (IV) f (x) = ln(1 2x) .
1+ cos x
(17)(本小题 13 分)
为了解客户对 A, B 两家快递公司的配送时效和服务满意度情况,现随机获得了某地区客户对这两家快
递公司评价的调查问卷. 已知 A, B 两家公司的调查问卷分别有120份和80 份,全部数据统计如下:
快递公司 A快递公司 B 快递公司
项目
配送时效 服务满意度 配送时效 服务满意度
评价分数 份数
85≤ x≤ 95 29 24 16 12
75≤ x 85 47 56 40 48
65≤ x 75 44 40 24 20
假设客户对 A, B 两家快递公司的评价相互独立. 用频率估计概率.
(Ⅰ)从该地区选择 A快递公司的客户中随机抽取1人,估计该客户对 A快递公司配送时效的评价不低于
75分的概率;
(Ⅱ)分别从该地区 A和 B 快递公司的样本调查问卷中,各随机抽取1份,记 X 为这 2 份问卷中的服务满
意度评价不低于 75 分的份数,求 X 的分布列和数学期望;
(Ⅲ)记评价分数 x≥ 85 为“优秀”等级, 75≤ x 85 为“良好”等级, 65≤ x 75为“一般”等级. 已知
小王比较看重配送时效的等级,根据该地区 A, B 两家快递公司配送时效的样本评价分数的等级情况,你认
为小王选择 A, B 哪家快递公司合适?说明理由.
(18)(本小题 13 分)
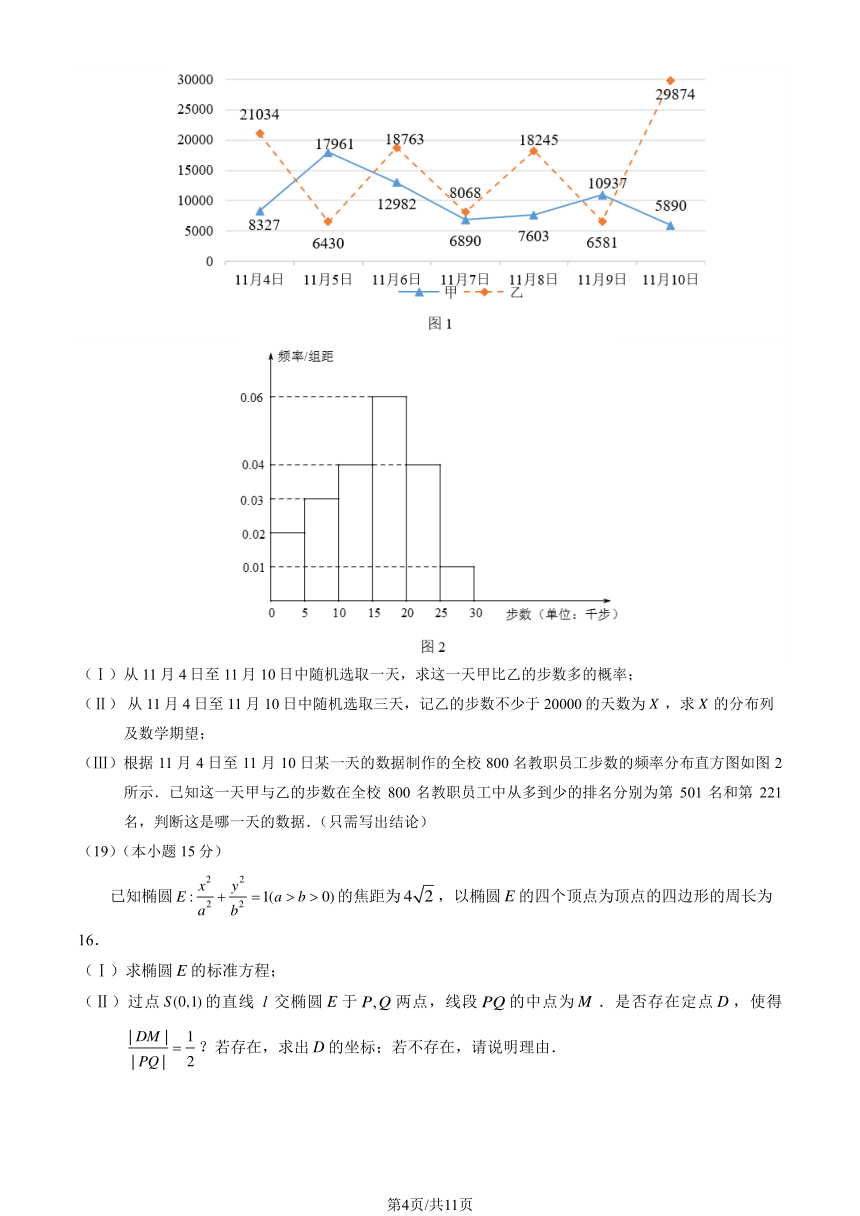
某学校开展健步走活动,要求学校教职员工上传 11 月 4 日至 11 月 10 日的步数信息.教师甲、乙这七
天的步数情况如图 1 所示.
第3页/共11页
(Ⅰ)从 11 月 4 日至 11 月 10 日中随机选取一天,求这一天甲比乙的步数多的概率;
(Ⅱ) 从 11 月 4 日至 11 月 10 日中随机选取三天,记乙的步数不少于 20000 的天数为 X ,求 X 的分布列
及数学期望;
(Ⅲ)根据 11 月 4 日至 11 月 10 日某一天的数据制作的全校 800 名教职员工步数的频率分布直方图如图 2
所示.已知这一天甲与乙的步数在全校 800 名教职员工中从多到少的排名分别为第 501 名和第 221
名,判断这是哪一天的数据.(只需写出结论)
(19)(本小题 15 分)
2 2
x y
已知椭圆 E : + =1(a b 0)的焦距为 4 2 ,以椭圆 E 的四个顶点为顶点的四边形的周长为
2 2
a b
16.
(Ⅰ)求椭圆 E 的标准方程;
(Ⅱ)过点 S (0,1) 的直线 l 交椭圆 E 于 P,Q 两点,线段 PQ 的中点为 M .是否存在定点 D ,使得
| DM | 1
= ?若存在,求出 D 的坐标;若不存在,请说明理由.
| PQ | 2
第4页/共11页
(20)(本小题 15 分)
m
已知函数 f (x) = + ln(x 1)2 ,其中 m R .
(x 1)
(Ⅰ)当m = 1时,求曲线 y = f (x) 在点 (2, f (2)) 处的切线方程;
(Ⅱ)若 f (x) 在 (2,+ )上存在极值,求实数m 的取值范围;
(Ⅲ)求 f (x) 的零点个数.
(21)(本小题 15 分)
有穷数列 an 共有m 项 (m≥ 3).其各项均为整数,且任意两项均不相等.
bi = ai ai+1 (i =1,2, ,m 1),bi ≤bi+1 (i =1,2, ,m 2).
(Ⅰ)若 a an :0,1, 3.求a3的取值范围;
5 4
(Ⅱ)若m = 5,当 ai 取最小值时,求 bi 的最大值;
i=1 i=1
m 1
(Ⅲ)若1≤ ai ≤ m (i =1,2,...,m), bk = m+1,求 m的所有可能取值.
k=1
第5页/共11页
参考答案
一、选择题(共 10 小题,每小题 4 分,共 40 分)
(1)A (2)C (3)C (4)B (5) D
(6)D (7)A (8)B (9)A (10)C
二、填空题(共 5 小题,每小题 5 分,共 25 分)
28
(11)162 (12)e (13)
3
(14) 4 ,3或 4 (注:第一空 2 分,第二空 3 分)
(15)② ③ (注:对一个 3 分,对 2 个 5 分)
三、解答题(共 6 小题,共 85 分)
(16)(本小题 14 分)
ex + 2 ex = (2x + x2 x(Ⅰ)解: f (x) = 2x x )e ………3 分
1 x 1
2 log x2 x 2 ln 2 log2 x ln 2
(Ⅱ)解: f (x) = x ln 2 = x ln 2 ………6 分
x )2 2x(2
cos x (1+ cos x) sin x ( sin x)
(Ⅲ)解: f (x) =
2
(1+ cos x)
cos x + cos2 x + sin2 x 1+ cos x 1
= = = ………10 分
(1+ cos x)2 (1+ cos x)2 1+ cos x
1 1 2
(IV)解: f (x) = (1 2x) = ( 2) = ………14 分
1 2x 1 2x 1 2x
(17)(本小题 13 分)
(Ⅰ)根据题中数据,该地区参与 A 快递公司调查的问卷共 120 份,
样本中对 A 快递公司配送时效的评价不低于 75 分的问卷共 29 + 47 = 76 份,
76 19
所以样本中对 A 快递公司配送时效的评价不低于 75 分的频率为 = ,
120 30
19
估计该地区客户对 A 快递公司配送时效的评价不低于 75 分的概率 ………3 分
30
(Ⅱ) X 的所有可能取值为 0, 1, 2 . ……… 4 分
记事件 C 为“从该地区 A 快递公司的样本调查问卷中随机抽取 1 份,该份问卷中的服务满意度评价不低于
75 分”,事件 D 为“从该地区 B 快递公司的样 本调查问卷中随机抽取 1 份,该份问卷中的服务满意度评价不
低于 75 分”.
由题设知,事件 C, D 相互独立,且
第6页/共11页
24+56 2 12+ 48 3
P (C ) = = ,P (D) = = , ……… 5 分
120 3 80 4
1 1 1
则 P (X = 0) = P(CD) = = ……… 6 分
3 4 12
1 3 2 1 5
P (X =1) = P(CD CD) = + = ……… 7 分
3 4 3 4 12
2 3 1
P (X = 2) = P(CD) = = ……… 8 分
3 4 2
所以 X 的分布列为:
X 0 1 2
1 5 1
P
12 12 2
……… 9 分
1 5 1 17
所以 E(X ) = 0 +1 + 2 = . ………10 分
12 12 2 12
(Ⅲ)答案不唯一.
答案示例 1:小王选择 A 快递公司合适,理由如下:
29
根据样本数据,估计 A 快递公司配送时效评价为 “优秀”的概率是 ,估计 B 快递公司配送时效评价为
120
1 29 1
“优秀”的概率是 ,因为 ,故小王选择 A 快递公司合适.
5 120 5
答案示例 2:小王选择 B 快递公司合适,理由如下:
19
由(Ⅰ)知,估计 A 快递公司配送时效评价为 “良好”以上的概率是 ; 由样本数据可知,估计 B 快递
30
16+ 40 56 7 19 7
公司配送时效评价为 “良好”以上的概率是 = = ,因为 ,故小王选择 B 快递公司
80 80 10 30 10
合适. ………13 分
(18)(本小题 13 分)
(Ⅰ)设“甲比乙的步数多”为事件 A.
在 11 月 4 日至 11 月 10 日这七天中,11 月 5 日与 11 月 9 日这两天甲比乙步数多,
2
所以 P(A) = . ………3 分
7
(Ⅱ)由图可知,7 天中乙的步数不少于 20000 步的天数共 2 天.
X 的所有可能取值为 0,1,2 ………4 分
第7页/共11页
C3C0 22 C C
1
4 C
1C2 1
P(X = 0) = 5 2 = , P(X =1) = 5 2 = , P(X = 2) = 5 2 =
C3 77 C
3 7
7 C
3 7
7 ………7 分
所以 X 的分布列为
X 0 1 2
2 4 1
P
7 7 7
………8 分
2 4 1 6
E(X ) = 0 +1 + 2 = ………10 分
7 7 7 7
(Ⅲ)11 月 6 日. ………13 分
(19)(本小题 15 分)
4 a2 + b2 =16,
a
2 =12,
(Ⅰ)由题意得 2c = 4 2, 解得
2
a2
b = 4.
= b2 + c2.
x2 y2
所以椭圆 E 的方程为 + =1. ………………5 分
12 4
DM 1
(Ⅱ)若存在定点 D,使得 = ,等价于以 PQ为直径的圆恒过定点 D .
PQ 2
2 2
当直线 l 的斜率不存在时, PQ为直径的圆的方程为 x + y = 4 ①, ……… 6 分
当直线 l 的斜率为 0 时,令 y =1,得 x = 3, ……… 7 分
2
因此 PQ为直径的圆的方程为 x2 + ( y 1) = 9 ②.
x = 0,
联立①②得 猜测点 D 的坐标为 (0, 2). ……… 8 分
y = 2,
设直线 l 的方程为 y = kx +1,
y = kx +1,
由 x2 y2 得 (3k 2 +1) x2 + 6kx 9 = 0. ……… 9 分
+ =1,
12 4
设 P (x1, y1 ) ,Q (x2 , y2 ),则
6k 9
x1 + x2 = , x1x2 = . ……… 11 分
3k 2 +1 3k 2 +1
所以 DP DQ = (x1, y1 + 2) (x2 , y2 + 2) ……… 12 分
第8页/共11页
= x1x2 + ( y1 + 2)( y2 + 2)
= x1x2 + (kx1 + 3)(kx2 + 3)
= (k 2 +1) x1x2 + 3k (x1 + x2 )+ 9 ……… 14 分
( 2 )
9 6k
= k +1 + 3k + 9
3k
2 +1 2 3k +1
= 0.
DM 1
综上,存在定点 D (0, 2),使得 = . ……… 15 分
PQ 2
(20)(本小题 15 分)
1
(Ⅰ)当m =1时, f (x) = + ln(x 1),
(x 1)2
2 1
则 f (x) = +3 , ……… 1 分 (x 1) x 1
故 f (2) = 2+1= 1, f (2) =1, ……… 2 分
y = f (x)在点 (2, f (2))处的切线方程为 y 1= (x 2),即 y = x + 3 ……… 3 分
2m 1 2m+ (x 1)2
(Ⅱ) f (x) = + = , ……… 4 分
(x 1)3 x 1 (x 1)3
当m 0时, f (x) 0, f (x)在 (2,+ ) 单调递增,此时无极值点, ……… 5 分
当m 0时,
2m+ (x 1)2
令 f (x) = = 0 x =1+ 2m 或3 x =1 2m , ……… 6 分 (x 1)
要使得 f (x) 在 (2,+ ) 上存在极值,
1
则需要 x =1+ 2m 2,解得m ( ,+ ) ……… 7 分
2
m
(Ⅲ)令 f (x) = + ln(x 1) = 0 m = (x 1)
2 ln(x 1)
2 , (x 1)
令 t = x 1 0 ,则m = t 2 ln t , ……… 8 分
2
记 g (t ) = t ln t ,则 g (t ) = 2t ln t t = t (2ln t +1), ……… 9 分
1
当 g t 0, g tt e 2 时, ( ) ( )单调递减, ……… 10 分
1
1
1
当 g t 0, g t g e 2 =0 t e 2 时, ( ) ( )单调递增,且 , ……… 11 分
2e
当 t 1时, g (t ) 0,
而当 t = e2 时, g (t ) = e
4 2 = 2e4 0, ……… 12 分
第9页/共11页
作出 g (t )的大致图象如下:
1
故当m 时,无零点, ……… 13 分
2e
1
当m = 或m 0时,一个零点, ……… 14 分
2e
1
当0 m 时,两个零点, ……… 15 分
2e
.
注:学生如果用其他方法,按步骤给分
(21)(本小题 15 分)
(Ⅰ)由题设b1 =| 0 1|=1 b2 =|1 a3 |,则 |1 a3 | 1,即1 a3 1或1 a3 1,
所以 a 2或 a3 03 ,任意两项均不相等,故 a3 0、 a3 1,
故a3的取值范围 a3 ( ,0) [2,+ )且 a3 Z ; ……… 4 分
5
(Ⅱ)由{ an }各项均为整数,任意两项均不相等,要使 ai 最小,即 ai 尽量小,
i=1
5
则 ( ai )min = 0+1+1+ 2+ 2,故{an}中的前 5 项为 2, 1,0,1,2 ,……… 5 分
i=1
4
要使 b | a a | + | a a | + | ai 最大,即 1 2 2 3 3 a4 | + | a4 a5 |最大, ……… 6 分
i=1
而bi bi+1,则 | a1 a2 | | a2 a3 | | a3 a4 | | a4 a5 |
a4 a5 尽可能大,所以 a4 a5 = 4,所以 a4 a5 = 4
a4 = 2 a4 = 2
所以, 或
a5 = 2 a5 = 2
不妨令 a5 = 2,只需依次使 | a4 a5 |,| a3 a4 |,| a2 a3 |,| a1 a2 | 取到最大,
要使 | a4 a5 |最大,则 a4 = 2; ……… 7 分
要使 | a3 a4 |最大,则 a3 =1; ……… 8 分
要使 | a2 a3 |最大,则 a2 = 1,故 a1 = 0; ……… 9 分
此时 | a4 a5 |= 4 | a3 a4 |= 3 | a2 a3 |= 2 | a1 a2 |=1,
第10页/共11页
4
综上, bi =1+ 2+3+ 4 =10 . ……… 10 分
i=1 max
m 1 m 1
(Ⅲ)对于1 ai m (i =1,2,...,m),则 bk 的最小值为m 1,而 bk = m+1 m 1,
k=1 k=1
由 (m +1) (m 1) = 2,且bi bi+1 (i =1,2, ,m 2),
所以{bm 1}有如下情况:①最后一项为 3,前面各项都为 1;②最后两项为 2,前面各项都为 1;
m = 3,数列{bm 1}不可能出现 3,或同时出现两个 2,排除;
m = 4 ,数列{am}为3, 2,1, 4,对应数列{bm 1}为1,1,3,故存在满足题设的情况;
m = 5,以下过程中 x N* ,
若存在满足①的数列{bm 1}元素依次为1,1,1,3,
令数列{a }前 4 项为 x, x +1, x + 2, x + 3m ,则第 5 项为 x(存在重复项,舍)或 x + 6,
而第 5 项为 x + 6 5,不满足题设;
若存在满足②的数列{bm 1}元素依次为1,1, 2, 2,
令数列{am}前 3 项为 x, x +1, x + 2,则第 4 项为 x(存在重复项,舍)或 x + 4 ,
第 4 项为 x + 4 ,则第 5 项为 x + 2 (存在重复项,舍)或 x + 6,而 x + 6 5不满足题设;
同上讨论,m 6时不可能存在满足题设的数列{am};
综上,m = 4 . ……… 15 分
第11页/共11页
数 学
2024.07
本试卷共 6 页,150 分。考试时长 120 分钟。考生务必将答案答在答题纸上,在试卷上作答无效。考
试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共 40 分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
x
(1)函数 y = 2 在 x = 1处的导数值为
1
(A) 2ln 2 (B)
ln 2
(C)1 (D) 2
(2)函数 3y = x + 2 在区间 [1, 2]上的平均变化率为
(A) 3 (B) 5
(C) 7 (D) 9
(3)已知数列 an 满足 an+1 = 2an , a2 = 4 ,则数列 an 的前 4 项和等于
(A)16 (B) 24
(C) 30 (D) 62
1
( )在 ( x )64 的展开式中,常数项为
x
(A) 15 (B)15
(C)30 (D)360
(5)用 0,1,2,3,4 可以组成无重复数字的两位数的个数为
(A) 20 (B) 25
(C)15 (D)16
(6)曲线 y = cos x在 x = 0 处的切线方程为
(A) y = 0 (B) y = 1
(C) y = x (D) y =1
第1页/共11页
3 2
(7)已知函数 f (x) = x + ax + x +1(a R) 有两个极值点 x1 , x2 (x1 x2 ) ,则
(A) a 3 或 a 3 (B) x 是 f (x)1 的极小值点
1 1
(C) x1 + x2 = (D) x1x2 =
3 3
(8)设 a1,a2 ,a3 , a6 是1,2,3, ,6 的一个排列. 且满足 | a1 a2 |≥| a2 a3 |≥ ≥| a5 a6 | ,
则 | a1 a2 | + | a2 a3 | + + | a5 a6 | 的最大值是
(A)17 (B)15
(C)13 (D)11
(9)设{a }是公比为 q(q 1)的无穷等比数列, Sn 为其前 n项和, a1 0 . 则“ q 0n ”
是“ Sn 存在最小值”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(10)已知数列 an 满足, n
*
N , a4n 3 = 1, a4n 1 =1, a2n = an ,该数列的前 n 项
和为 Sn ,则下列论断中错.误.的是
(A) a31 =1 (B) a2024 = 1
(C) 非零常数T ,使得 an+T = an (D) n
*
N ,都有 S n = 2 2
第二部分 (非选择题 共 110 分)
二、填空题共 5 小题,每小题 5 分,共 25 分。
(11)2023 年起延庆区将利用三年时间重点打造“延庆东南山·九沟十八湾”乡村振兴品牌,旨在借助延
庆区东南部浅山区和山区的沟域空间结构、功能布局及秀美山水,构建 9 条各具特色的生态沟域廊
道、18 条生态沟域农文体康旅体验湾,全面推动延庆区乡村振兴,打造新时代首都生态沟域绿色发
展新典范. 小明打算从九沟十八湾中选出一沟一湾去旅游,则不同的选法有_________种.
(12)已知函数 f (x) = log x (a 0且a 1)a ,若 f (1) = 1,则 a = _________.
1
( 313)已知函数 f (x) = x 4x + 4 ,则 f (x) 在区间[ 3, 3] 上的最大值为_________.
3
(14)已知数列 an 是各项均为正数的等比数列, Sn 为其前 n项和, a1a3 =16 , S3 =14,
则 a2 = _________;记Tn = a1a2 an (n =1,2, ) ,若存在 n0
*
N 使得Tn 最大,
则 n0 的值为_________.
( )已知数列{ a }的各项均为正数,满足 a = ca 215 n n+1 n + an ,其中常数 c R . 给出下列四个判断:
第2页/共11页
1
①若 a1 =1, c 0 ,则 an (n 2);
n +1
1
②若 c = 1,则 an (n 2);
n +1
③若 c =1, an n (n 2),则 a1 1;
④ a1 =1,不存在实数 c ,使得 an n (n 2).
其中所有正确判断的序号是_________.
三、解答题共 6 小题,共 85 分。解答应写出文字说明,证明过程或演算步骤。
(16)(本小题 14 分)
求下列函数的导函数.
(Ⅰ) 2 x
log x
f (x) = x e ; (Ⅱ) f (x) = 2 ;
2x
sin x
(Ⅲ) f (x) = ; (IV) f (x) = ln(1 2x) .
1+ cos x
(17)(本小题 13 分)
为了解客户对 A, B 两家快递公司的配送时效和服务满意度情况,现随机获得了某地区客户对这两家快
递公司评价的调查问卷. 已知 A, B 两家公司的调查问卷分别有120份和80 份,全部数据统计如下:
快递公司 A快递公司 B 快递公司
项目
配送时效 服务满意度 配送时效 服务满意度
评价分数 份数
85≤ x≤ 95 29 24 16 12
75≤ x 85 47 56 40 48
65≤ x 75 44 40 24 20
假设客户对 A, B 两家快递公司的评价相互独立. 用频率估计概率.
(Ⅰ)从该地区选择 A快递公司的客户中随机抽取1人,估计该客户对 A快递公司配送时效的评价不低于
75分的概率;
(Ⅱ)分别从该地区 A和 B 快递公司的样本调查问卷中,各随机抽取1份,记 X 为这 2 份问卷中的服务满
意度评价不低于 75 分的份数,求 X 的分布列和数学期望;
(Ⅲ)记评价分数 x≥ 85 为“优秀”等级, 75≤ x 85 为“良好”等级, 65≤ x 75为“一般”等级. 已知
小王比较看重配送时效的等级,根据该地区 A, B 两家快递公司配送时效的样本评价分数的等级情况,你认
为小王选择 A, B 哪家快递公司合适?说明理由.
(18)(本小题 13 分)
某学校开展健步走活动,要求学校教职员工上传 11 月 4 日至 11 月 10 日的步数信息.教师甲、乙这七
天的步数情况如图 1 所示.
第3页/共11页
(Ⅰ)从 11 月 4 日至 11 月 10 日中随机选取一天,求这一天甲比乙的步数多的概率;
(Ⅱ) 从 11 月 4 日至 11 月 10 日中随机选取三天,记乙的步数不少于 20000 的天数为 X ,求 X 的分布列
及数学期望;
(Ⅲ)根据 11 月 4 日至 11 月 10 日某一天的数据制作的全校 800 名教职员工步数的频率分布直方图如图 2
所示.已知这一天甲与乙的步数在全校 800 名教职员工中从多到少的排名分别为第 501 名和第 221
名,判断这是哪一天的数据.(只需写出结论)
(19)(本小题 15 分)
2 2
x y
已知椭圆 E : + =1(a b 0)的焦距为 4 2 ,以椭圆 E 的四个顶点为顶点的四边形的周长为
2 2
a b
16.
(Ⅰ)求椭圆 E 的标准方程;
(Ⅱ)过点 S (0,1) 的直线 l 交椭圆 E 于 P,Q 两点,线段 PQ 的中点为 M .是否存在定点 D ,使得
| DM | 1
= ?若存在,求出 D 的坐标;若不存在,请说明理由.
| PQ | 2
第4页/共11页
(20)(本小题 15 分)
m
已知函数 f (x) = + ln(x 1)2 ,其中 m R .
(x 1)
(Ⅰ)当m = 1时,求曲线 y = f (x) 在点 (2, f (2)) 处的切线方程;
(Ⅱ)若 f (x) 在 (2,+ )上存在极值,求实数m 的取值范围;
(Ⅲ)求 f (x) 的零点个数.
(21)(本小题 15 分)
有穷数列 an 共有m 项 (m≥ 3).其各项均为整数,且任意两项均不相等.
bi = ai ai+1 (i =1,2, ,m 1),bi ≤bi+1 (i =1,2, ,m 2).
(Ⅰ)若 a an :0,1, 3.求a3的取值范围;
5 4
(Ⅱ)若m = 5,当 ai 取最小值时,求 bi 的最大值;
i=1 i=1
m 1
(Ⅲ)若1≤ ai ≤ m (i =1,2,...,m), bk = m+1,求 m的所有可能取值.
k=1
第5页/共11页
参考答案
一、选择题(共 10 小题,每小题 4 分,共 40 分)
(1)A (2)C (3)C (4)B (5) D
(6)D (7)A (8)B (9)A (10)C
二、填空题(共 5 小题,每小题 5 分,共 25 分)
28
(11)162 (12)e (13)
3
(14) 4 ,3或 4 (注:第一空 2 分,第二空 3 分)
(15)② ③ (注:对一个 3 分,对 2 个 5 分)
三、解答题(共 6 小题,共 85 分)
(16)(本小题 14 分)
ex + 2 ex = (2x + x2 x(Ⅰ)解: f (x) = 2x x )e ………3 分
1 x 1
2 log x2 x 2 ln 2 log2 x ln 2
(Ⅱ)解: f (x) = x ln 2 = x ln 2 ………6 分
x )2 2x(2
cos x (1+ cos x) sin x ( sin x)
(Ⅲ)解: f (x) =
2
(1+ cos x)
cos x + cos2 x + sin2 x 1+ cos x 1
= = = ………10 分
(1+ cos x)2 (1+ cos x)2 1+ cos x
1 1 2
(IV)解: f (x) = (1 2x) = ( 2) = ………14 分
1 2x 1 2x 1 2x
(17)(本小题 13 分)
(Ⅰ)根据题中数据,该地区参与 A 快递公司调查的问卷共 120 份,
样本中对 A 快递公司配送时效的评价不低于 75 分的问卷共 29 + 47 = 76 份,
76 19
所以样本中对 A 快递公司配送时效的评价不低于 75 分的频率为 = ,
120 30
19
估计该地区客户对 A 快递公司配送时效的评价不低于 75 分的概率 ………3 分
30
(Ⅱ) X 的所有可能取值为 0, 1, 2 . ……… 4 分
记事件 C 为“从该地区 A 快递公司的样本调查问卷中随机抽取 1 份,该份问卷中的服务满意度评价不低于
75 分”,事件 D 为“从该地区 B 快递公司的样 本调查问卷中随机抽取 1 份,该份问卷中的服务满意度评价不
低于 75 分”.
由题设知,事件 C, D 相互独立,且
第6页/共11页
24+56 2 12+ 48 3
P (C ) = = ,P (D) = = , ……… 5 分
120 3 80 4
1 1 1
则 P (X = 0) = P(CD) = = ……… 6 分
3 4 12
1 3 2 1 5
P (X =1) = P(CD CD) = + = ……… 7 分
3 4 3 4 12
2 3 1
P (X = 2) = P(CD) = = ……… 8 分
3 4 2
所以 X 的分布列为:
X 0 1 2
1 5 1
P
12 12 2
……… 9 分
1 5 1 17
所以 E(X ) = 0 +1 + 2 = . ………10 分
12 12 2 12
(Ⅲ)答案不唯一.
答案示例 1:小王选择 A 快递公司合适,理由如下:
29
根据样本数据,估计 A 快递公司配送时效评价为 “优秀”的概率是 ,估计 B 快递公司配送时效评价为
120
1 29 1
“优秀”的概率是 ,因为 ,故小王选择 A 快递公司合适.
5 120 5
答案示例 2:小王选择 B 快递公司合适,理由如下:
19
由(Ⅰ)知,估计 A 快递公司配送时效评价为 “良好”以上的概率是 ; 由样本数据可知,估计 B 快递
30
16+ 40 56 7 19 7
公司配送时效评价为 “良好”以上的概率是 = = ,因为 ,故小王选择 B 快递公司
80 80 10 30 10
合适. ………13 分
(18)(本小题 13 分)
(Ⅰ)设“甲比乙的步数多”为事件 A.
在 11 月 4 日至 11 月 10 日这七天中,11 月 5 日与 11 月 9 日这两天甲比乙步数多,
2
所以 P(A) = . ………3 分
7
(Ⅱ)由图可知,7 天中乙的步数不少于 20000 步的天数共 2 天.
X 的所有可能取值为 0,1,2 ………4 分
第7页/共11页
C3C0 22 C C
1
4 C
1C2 1
P(X = 0) = 5 2 = , P(X =1) = 5 2 = , P(X = 2) = 5 2 =
C3 77 C
3 7
7 C
3 7
7 ………7 分
所以 X 的分布列为
X 0 1 2
2 4 1
P
7 7 7
………8 分
2 4 1 6
E(X ) = 0 +1 + 2 = ………10 分
7 7 7 7
(Ⅲ)11 月 6 日. ………13 分
(19)(本小题 15 分)
4 a2 + b2 =16,
a
2 =12,
(Ⅰ)由题意得 2c = 4 2, 解得
2
a2
b = 4.
= b2 + c2.
x2 y2
所以椭圆 E 的方程为 + =1. ………………5 分
12 4
DM 1
(Ⅱ)若存在定点 D,使得 = ,等价于以 PQ为直径的圆恒过定点 D .
PQ 2
2 2
当直线 l 的斜率不存在时, PQ为直径的圆的方程为 x + y = 4 ①, ……… 6 分
当直线 l 的斜率为 0 时,令 y =1,得 x = 3, ……… 7 分
2
因此 PQ为直径的圆的方程为 x2 + ( y 1) = 9 ②.
x = 0,
联立①②得 猜测点 D 的坐标为 (0, 2). ……… 8 分
y = 2,
设直线 l 的方程为 y = kx +1,
y = kx +1,
由 x2 y2 得 (3k 2 +1) x2 + 6kx 9 = 0. ……… 9 分
+ =1,
12 4
设 P (x1, y1 ) ,Q (x2 , y2 ),则
6k 9
x1 + x2 = , x1x2 = . ……… 11 分
3k 2 +1 3k 2 +1
所以 DP DQ = (x1, y1 + 2) (x2 , y2 + 2) ……… 12 分
第8页/共11页
= x1x2 + ( y1 + 2)( y2 + 2)
= x1x2 + (kx1 + 3)(kx2 + 3)
= (k 2 +1) x1x2 + 3k (x1 + x2 )+ 9 ……… 14 分
( 2 )
9 6k
= k +1 + 3k + 9
3k
2 +1 2 3k +1
= 0.
DM 1
综上,存在定点 D (0, 2),使得 = . ……… 15 分
PQ 2
(20)(本小题 15 分)
1
(Ⅰ)当m =1时, f (x) = + ln(x 1),
(x 1)2
2 1
则 f (x) = +3 , ……… 1 分 (x 1) x 1
故 f (2) = 2+1= 1, f (2) =1, ……… 2 分
y = f (x)在点 (2, f (2))处的切线方程为 y 1= (x 2),即 y = x + 3 ……… 3 分
2m 1 2m+ (x 1)2
(Ⅱ) f (x) = + = , ……… 4 分
(x 1)3 x 1 (x 1)3
当m 0时, f (x) 0, f (x)在 (2,+ ) 单调递增,此时无极值点, ……… 5 分
当m 0时,
2m+ (x 1)2
令 f (x) = = 0 x =1+ 2m 或3 x =1 2m , ……… 6 分 (x 1)
要使得 f (x) 在 (2,+ ) 上存在极值,
1
则需要 x =1+ 2m 2,解得m ( ,+ ) ……… 7 分
2
m
(Ⅲ)令 f (x) = + ln(x 1) = 0 m = (x 1)
2 ln(x 1)
2 , (x 1)
令 t = x 1 0 ,则m = t 2 ln t , ……… 8 分
2
记 g (t ) = t ln t ,则 g (t ) = 2t ln t t = t (2ln t +1), ……… 9 分
1
当 g t 0, g tt e 2 时, ( ) ( )单调递减, ……… 10 分
1
1
1
当 g t 0, g t g e 2 =0 t e 2 时, ( ) ( )单调递增,且 , ……… 11 分
2e
当 t 1时, g (t ) 0,
而当 t = e2 时, g (t ) = e
4 2 = 2e4 0, ……… 12 分
第9页/共11页
作出 g (t )的大致图象如下:
1
故当m 时,无零点, ……… 13 分
2e
1
当m = 或m 0时,一个零点, ……… 14 分
2e
1
当0 m 时,两个零点, ……… 15 分
2e
.
注:学生如果用其他方法,按步骤给分
(21)(本小题 15 分)
(Ⅰ)由题设b1 =| 0 1|=1 b2 =|1 a3 |,则 |1 a3 | 1,即1 a3 1或1 a3 1,
所以 a 2或 a3 03 ,任意两项均不相等,故 a3 0、 a3 1,
故a3的取值范围 a3 ( ,0) [2,+ )且 a3 Z ; ……… 4 分
5
(Ⅱ)由{ an }各项均为整数,任意两项均不相等,要使 ai 最小,即 ai 尽量小,
i=1
5
则 ( ai )min = 0+1+1+ 2+ 2,故{an}中的前 5 项为 2, 1,0,1,2 ,……… 5 分
i=1
4
要使 b | a a | + | a a | + | ai 最大,即 1 2 2 3 3 a4 | + | a4 a5 |最大, ……… 6 分
i=1
而bi bi+1,则 | a1 a2 | | a2 a3 | | a3 a4 | | a4 a5 |
a4 a5 尽可能大,所以 a4 a5 = 4,所以 a4 a5 = 4
a4 = 2 a4 = 2
所以, 或
a5 = 2 a5 = 2
不妨令 a5 = 2,只需依次使 | a4 a5 |,| a3 a4 |,| a2 a3 |,| a1 a2 | 取到最大,
要使 | a4 a5 |最大,则 a4 = 2; ……… 7 分
要使 | a3 a4 |最大,则 a3 =1; ……… 8 分
要使 | a2 a3 |最大,则 a2 = 1,故 a1 = 0; ……… 9 分
此时 | a4 a5 |= 4 | a3 a4 |= 3 | a2 a3 |= 2 | a1 a2 |=1,
第10页/共11页
4
综上, bi =1+ 2+3+ 4 =10 . ……… 10 分
i=1 max
m 1 m 1
(Ⅲ)对于1 ai m (i =1,2,...,m),则 bk 的最小值为m 1,而 bk = m+1 m 1,
k=1 k=1
由 (m +1) (m 1) = 2,且bi bi+1 (i =1,2, ,m 2),
所以{bm 1}有如下情况:①最后一项为 3,前面各项都为 1;②最后两项为 2,前面各项都为 1;
m = 3,数列{bm 1}不可能出现 3,或同时出现两个 2,排除;
m = 4 ,数列{am}为3, 2,1, 4,对应数列{bm 1}为1,1,3,故存在满足题设的情况;
m = 5,以下过程中 x N* ,
若存在满足①的数列{bm 1}元素依次为1,1,1,3,
令数列{a }前 4 项为 x, x +1, x + 2, x + 3m ,则第 5 项为 x(存在重复项,舍)或 x + 6,
而第 5 项为 x + 6 5,不满足题设;
若存在满足②的数列{bm 1}元素依次为1,1, 2, 2,
令数列{am}前 3 项为 x, x +1, x + 2,则第 4 项为 x(存在重复项,舍)或 x + 4 ,
第 4 项为 x + 4 ,则第 5 项为 x + 2 (存在重复项,舍)或 x + 6,而 x + 6 5不满足题设;
同上讨论,m 6时不可能存在满足题设的数列{am};
综上,m = 4 . ……… 15 分
第11页/共11页
同课章节目录
