河南省焦作市博爱县第一中学20232024学年高一下学期6月期末考试数学试题(含解析)
文档属性
| 名称 | 河南省焦作市博爱县第一中学20232024学年高一下学期6月期末考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 17:40:04 | ||
图片预览




文档简介
焦作市博爱县第一中学2023—2024学年高一(下)期末考试
数 学 试 题
考生注意: 1.答题前,考生务必用黑色签字笔将自己的姓名、准考证号、座位号在答题卡上填写清楚; 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,在试卷上作答无效; 3.考试结束后,请将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知,,分别是三内角,,的对边,则“”是“为直角三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.设,,,则下列关系正确的是( )
A. B. C. D.
3.已知函数,则关于方程的根个数不可能是( )
A.0个 B.1个 C.2个 D.3个
4.在明代珠算发明之前,我们的先祖从春秋开始多是用算筹为工具来记数、列式和计算的.算筹实际上是一根根相同长度的小木棍,如图是利用算筹表示数1~9的一种方法,例如:47可以表示为“”,已知用算筹表示一个不含“0”且没有重复数字的三位数共有504种等可能的结果,则这个数至少要用8根小木棍的概率为( )
A. B. C. D.
5.如图,圆锥 的底面直径和高均为,过 上一点 作平行于底面的截面,以该截面为底面挖去一个圆柱,我们称该圆柱为圆锥的内接圆柱.则该圆锥的内接圆柱侧面积的最大值为( )
A. B. C. D.
6.我国南宋时期著名的数学家秦九韶在其著作《数书九章》中,提出了已知三角形三边长求其面积的公式,求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂減上,余四约之,为实.为从隅,开平方得积"翻泽成公式,即 ,其中 分别为 中角 的对边, 为 的面积.现有面积为 的 满足 ,则其内切圆的半径是( )
A. B. C. D.
7.已知中,,,若最短边的长度为,则最长边的长度是( )
A.3 B.8 C. D.
8.锐角的内角A,B,C的对边分别为a,b,c,若,,则的取值范围是( )
A. B.
C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分,若只有2个正确选项,每选对1个得3分;若只有3个正确选项,每选对1个得2分.
9.下列论述正确的有( )
A.样本相关系数r越大,两个变量的线性相关程度越强;反之,线性相关程度越弱
B.数据49,21,32,29,38,65,30,50的第60百分位数为38
C.若随机变量,且,则
D.一组样本数据,其中是最小值,是最大值,则的标准差不小于的标准差
10.已知实数,满足,则下列不等式恒成立的是( )
A.
B.若,,则
C.
D.若,,则
11.已知是双曲线的右焦点,为其左支上一点,点,则( )
A.双曲线的焦距为6
B.点到渐近线的距离为2
C.的最小值为
D.若,则的面积为
三、填空题:本大题共3个小题,每小题5分,共15分.
12.已知函数在上的值域为,则的值为 .
13.函数(,)的部分图象如图所示,直线()与这部分图象相交于三个点,横坐标从左到右分别为,,,则______.
14.已知的内角,,所对的边分别为,,,若,,且,则 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知函数.
(1)若的定义域为,求的取值范围;
(2)若,使得在区间上单调递增,且值域为,求的取值范围.
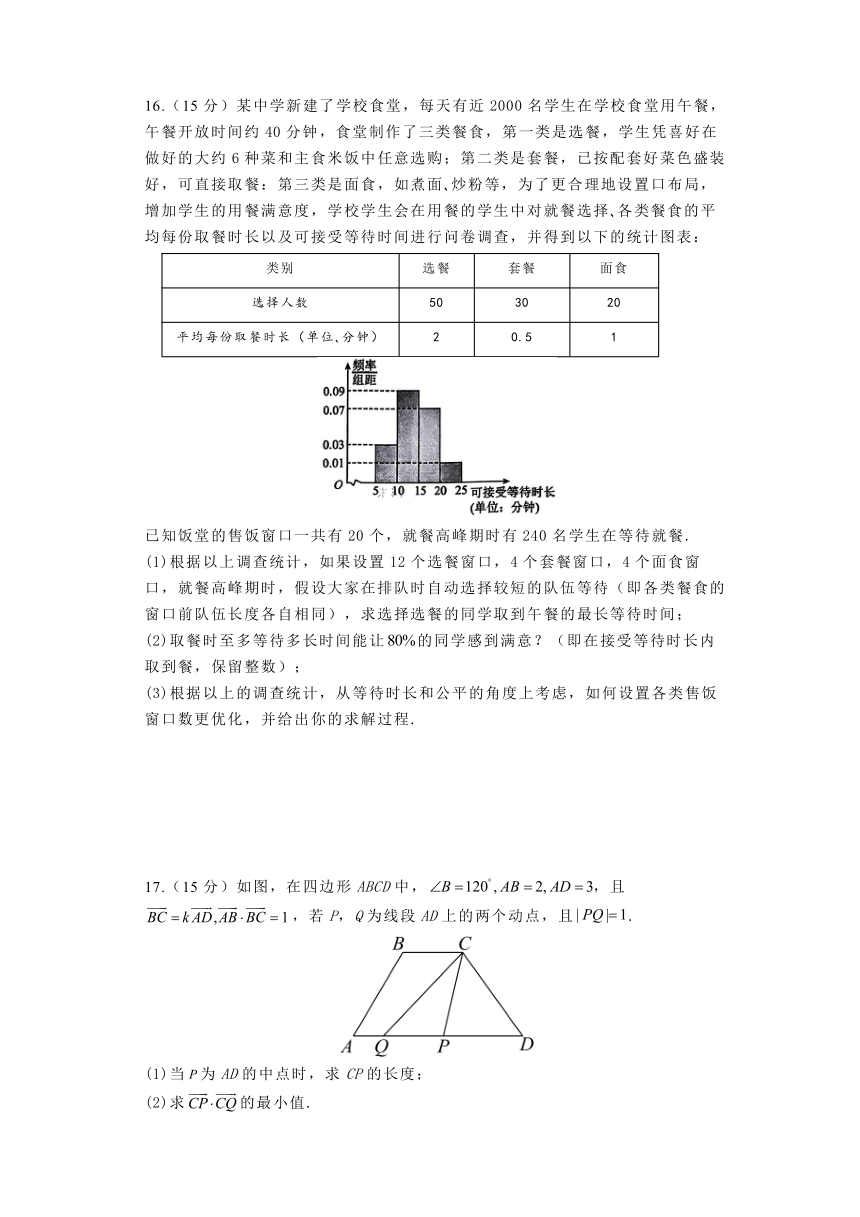
16.(15分)某中学新建了学校食堂,每天有近2000名学生在学校食堂用午餐,午餐开放时间约40分钟,食堂制作了三类餐食,第一类是选餐,学生凭喜好在做好的大约6种菜和主食米饭中任意选购;第二类是套餐,已按配套好菜色盛装好,可直接取餐:第三类是面食,如煮面 炒粉等,为了更合理地设置口布局,增加学生的用餐满意度,学校学生会在用餐的学生中对就餐选择 各类餐食的平均每份取餐时长以及可接受等待时间进行问卷调查,并得到以下的统计图表:
类别 选餐 套餐 面食
选择人数 50 30 20
平均每份取餐时长(单位 分钟) 2 0.5 1
已知饭堂的售饭窗口一共有20个,就餐高峰期时有240名学生在等待就餐.
(1)根据以上调查统计,如果设置12个选餐窗口,4个套餐窗口,4个面食窗口,就餐高峰期时,假设大家在排队时自动选择较短的队伍等待(即各类餐食的窗口前队伍长度各自相同),求选择选餐的同学取到午餐的最长等待时间;
(2)取餐时至多等待多长时间能让的同学感到满意?(即在接受等待时长内取到餐,保留整数);
(3)根据以上的调查统计,从等待时长和公平的角度上考虑,如何设置各类售饭窗口数更优化,并给出你的求解过程.
17.(15分)如图,在四边形ABCD中,,且,若P,Q为线段AD上的两个动点,且.
(1)当为AD的中点时,求CP的长度;
(2)求的最小值.
18.(17分)如图,在正三棱柱中,为的中点.
(1)证明:平面.
(2)求异面直线与所成角的余弦值.
(3)在上是否存在点,使得平面平面?若存在,求出的值;若不存在,说明理由.
19.(17分)在①,②,③这三个条件中任选一个,补充在下面的问题中,并解答该问题.
在 中,内角的对边分别是,且满足_______,.
(1)若,求的面积;
(2)求周长的取值范围.
数学·参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】A
【解析】在中,由正弦定理可得:,
由,可得:,
所以,因为,所以,
即,所以,
因为,所以,
所以,所以为直角三角形,
故“”是“为直角三角形”的充分条件;
若为直角三角形,设,,
则,所以,
所以,
所以“”不是“为直角三角形”的必要条件;
即“”是“为直角三角形”的充分不必要条件.
故选:A.
2.【答案】B
【解析】∵,
∴,∴;
,∴;
,∴,
∴.
故选:B.
3.【答案】C
【解析】作出函数的图象,如图所示:
将原问题转化为直线(过定点)与函数的图象交点的个数,由图可知,当时,直线与函数的图象只有一个交点;
当时,直线与函数的图象没有交点;
当时,直线与函数的图象有三个交点;
所以直线与函数的图象不可能有两个交点.
故选:C.
4.【答案】D
【解析】至少要用8根小木棍的对立事件为用5根,6根,7根这三种情况.
用5根小木棍为1,2,6这一种情况,组成三位数包括6个样本点,
用6根有1,2,3;1,2,7;1,6,3;1,6,7这四种情况,每种情况包含6个样本点,共24个样本点
用7根有1,2,4;1,2,8;1,6,4;1,6,8;1,3,7;2,6,7;2,6,3这七种情况,
每种情况包含6个样本点,共42个样本点
又表示一个不含“0”且没有重复数字的三位数有504种情况
故至少要用8根小木棍的概率为1-,
故选:D.
5.【答案】C
【解析】圆锥轴截面如图所示,
设圆柱的底面半径为 , ,由 可知, ,即 ,所以 ,
故被挖去的圆柱的侧面积为 ,
当且仅当 时取等号,即 时,被挖去的圆柱的侧面积最大值为 .
故选:C
6.【答案】A
【解析】由正弦定理可得 ,设 ,则 ,解得 ,故 的三边长分别是 .设 的内切圆的半径是 ,则 ,所以 .
7.【答案】C
【解析】由题可知,
由,则,
由,则,,
则
,
故有,故,故,即,
则,由,则,
故.
故选:C.
8.【答案】B
【解析】因为,所以,
整理可得,即有.
又,所以,解得,所以,
于是.
因为三角形是锐角三角形,所以,所以,
所以的取值范围是.
故选B.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分,若只有2个正确选项,每选对1个得3分;若只有3个正确选项,每选对1个得2分.
9.【答案】BC
【解析】对于A:样本相关系数r的绝对值越大,两个变量的线性相关程度越强;反之,线性相关程度越弱,故A错误;
对于B:将数据按升序排列可得:21,29,30,32,38,49,50,65,
因为样本数据有8个,且,
所以第60百分位数为第5位数38,故B正确;
对于C:因为,且,则,
所以,故C正确;
对于D:新样本即对原样本剔除最大值和最小值,
可得新样本的波动性减小,
所以的标准差不大于的标准差,故D错误;
故选BC.
10.【答案】BCD
【解析】因为为上的增函数,所以.
因为函数在上有增有减,所以A中的不等式不恒成立,A错误;
因为函数在上单调递减,
所以当,,时,,故B正确;
因为在上单调递增,所以当时,,故C正确;
因为函数在上单调递增,
所以当,,时,,故D正确.
故选:BCD.
11.【答案】AC
【解析】如图:
由双曲线的标准方程,可知,,所以,所以双曲线的焦距为:,故A正确;
双曲线的渐近线为,即,点到渐近线的距离为:
,故B错误;
设双曲线的左焦点为,根据双曲线的定义:,
所以,故C正确;
在中,由,,,
由余弦定理得:,
所以,
所以,所以,故D错误.
故选:AC
三、填空题:本大题共3个小题,每小题5分,共15分.
12.【答案】6
【解析】函数的图像抛物线开口向上,对称轴方程为,
则,解得,
所以在上单调递增,所以即
所以为方程的两个根,即为方程的两个根,
由韦达定理有.
故答案为:6.
13.【答案】
【解析】由图可知,,即,
则解得,,故.
则,最小正周期为.
直线()与这部分图象相交于三个点,横坐标从左到右分别为,,,则由图可知,.
所以
.
14.【答案】
【解析】解:由题意,,
则由正弦定理可得,
∵,∴,∴,
又∵,则,
∴,
∴.又由,
可得:,则,
∴,即,则,
∴,即,由解得:,
∴由解得:,.
∴由正弦定理可得:,解得:,,
∴.
故答案为:
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)【答案】(1);(2).
【解析】(1)因为的定义域为,,
所以,即恒成立,
因为,,当时等号成立,
所以,即的取值范围为;
(2)因为函数在其定义域上为增函数,要使在区间上单调递增,则函数在区间上单调递增,又为增函数,
所以在上为增函数,显然时不合题意,
所以,且,
又在区间上单调递增,且值域为,
所以,即,
所以在上有两个不等实根,
则,解得,
所以的取值范围为.
16.(15分)【答案】(1)20分钟;(2)18分钟;(3)答案见解析
【解析】(1)由题意得就餐高峰期时选择选餐的总人数为人;这120人平均分布在12个选餐窗口,平均每个窗口等待就餐的人数为人,所以选择选餐的同学取到午餐的最长等待时间为分钟,
(2)由可接受等待时长的频率分布直方图可知,
分组为的频率分别为,
所以可接受等待时长在分钟以内的同学占0.05,即有的同学不满意
可接受等待时长在分钟以内的同学占,
即有的同学对等待时间少于15分钟感到满意,
所以至多等待的时间,能让的同学感到满意
,所以分钟,
至多等待18分钟,能让的同学感到满意.
(3)假设设置个选餐窗口,个套餐窗口,个面食窗口,
则各队伍的同学最长等待时间如下:
类别 选餐 套餐 面食
高峰期就餐总人数 120 72 48
各队伍长度(人)
最长等待时间(分钟)
依题意,从等待时长和公平的角度上考虑,则要求每个队伍的最长等待时间大致相同,即得,即有,
而,故,
因此建议设置选餐 套餐 面食三个类别的窗口数分别为15,2,3个.
17.(15分)【答案】(1);(2)
【解析】(1)由,得,
因为,所以,
又,
所以;
(2)设,,
则,
,
所以
,
当时,取到最小值,且为.
18.(17分)【答案】(1)证明见解析;(2);(3)存在,
【解析】(1)由正三棱柱的定义可知是等边三角形,平面.
因为平面,所以.
因为是等边三角形,D为的中点,所以.
因为,平面,且,
所以平面.
(2)如图,取的中点,连接,,则,
则是异面直线与CD所成的角或补角.
设,则,,,,
故,
即异面直线与CD所成角的余弦值为.
(3)在中,作,垂足为E.
因为平面,且平面,
所以.
因为平面,且,
所以平面.
因为平面BCE,所以平面平面.
设,则,,故.
因为,
所以,
则,,
所以.
故在上存在点E,使得平面平面,此时.
19.(17分)【答案】(1)任选一条件,面积皆为;(2).
【解析】(1)若选条件①, 由 及正弦定理, 得
即 , 化简得,
因为, 所以, 所以,因为 , 所以.
若选条件②, 由 及正弦定理, 得, 即, 化简得,
因为 , 所以, 所以,因为 , 所以.
若选条件③, 由 化简得,, 由余弦定理得, 即,因为 , 所以,
所以三个条件,都能得到.
由余弦定理得 , 即, 解得,
所以的面积.
(2)因为 , 由正弦定理得,
因为 ,
所以 ,
因为 , 所以,
所以 , 即, 所以周长的取值范围为.
第 page number 页,共 number of pages 页
数 学 试 题
考生注意: 1.答题前,考生务必用黑色签字笔将自己的姓名、准考证号、座位号在答题卡上填写清楚; 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,在试卷上作答无效; 3.考试结束后,请将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知,,分别是三内角,,的对边,则“”是“为直角三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.设,,,则下列关系正确的是( )
A. B. C. D.
3.已知函数,则关于方程的根个数不可能是( )
A.0个 B.1个 C.2个 D.3个
4.在明代珠算发明之前,我们的先祖从春秋开始多是用算筹为工具来记数、列式和计算的.算筹实际上是一根根相同长度的小木棍,如图是利用算筹表示数1~9的一种方法,例如:47可以表示为“”,已知用算筹表示一个不含“0”且没有重复数字的三位数共有504种等可能的结果,则这个数至少要用8根小木棍的概率为( )
A. B. C. D.
5.如图,圆锥 的底面直径和高均为,过 上一点 作平行于底面的截面,以该截面为底面挖去一个圆柱,我们称该圆柱为圆锥的内接圆柱.则该圆锥的内接圆柱侧面积的最大值为( )
A. B. C. D.
6.我国南宋时期著名的数学家秦九韶在其著作《数书九章》中,提出了已知三角形三边长求其面积的公式,求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂減上,余四约之,为实.为从隅,开平方得积"翻泽成公式,即 ,其中 分别为 中角 的对边, 为 的面积.现有面积为 的 满足 ,则其内切圆的半径是( )
A. B. C. D.
7.已知中,,,若最短边的长度为,则最长边的长度是( )
A.3 B.8 C. D.
8.锐角的内角A,B,C的对边分别为a,b,c,若,,则的取值范围是( )
A. B.
C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分,若只有2个正确选项,每选对1个得3分;若只有3个正确选项,每选对1个得2分.
9.下列论述正确的有( )
A.样本相关系数r越大,两个变量的线性相关程度越强;反之,线性相关程度越弱
B.数据49,21,32,29,38,65,30,50的第60百分位数为38
C.若随机变量,且,则
D.一组样本数据,其中是最小值,是最大值,则的标准差不小于的标准差
10.已知实数,满足,则下列不等式恒成立的是( )
A.
B.若,,则
C.
D.若,,则
11.已知是双曲线的右焦点,为其左支上一点,点,则( )
A.双曲线的焦距为6
B.点到渐近线的距离为2
C.的最小值为
D.若,则的面积为
三、填空题:本大题共3个小题,每小题5分,共15分.
12.已知函数在上的值域为,则的值为 .
13.函数(,)的部分图象如图所示,直线()与这部分图象相交于三个点,横坐标从左到右分别为,,,则______.
14.已知的内角,,所对的边分别为,,,若,,且,则 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知函数.
(1)若的定义域为,求的取值范围;
(2)若,使得在区间上单调递增,且值域为,求的取值范围.
16.(15分)某中学新建了学校食堂,每天有近2000名学生在学校食堂用午餐,午餐开放时间约40分钟,食堂制作了三类餐食,第一类是选餐,学生凭喜好在做好的大约6种菜和主食米饭中任意选购;第二类是套餐,已按配套好菜色盛装好,可直接取餐:第三类是面食,如煮面 炒粉等,为了更合理地设置口布局,增加学生的用餐满意度,学校学生会在用餐的学生中对就餐选择 各类餐食的平均每份取餐时长以及可接受等待时间进行问卷调查,并得到以下的统计图表:
类别 选餐 套餐 面食
选择人数 50 30 20
平均每份取餐时长(单位 分钟) 2 0.5 1
已知饭堂的售饭窗口一共有20个,就餐高峰期时有240名学生在等待就餐.
(1)根据以上调查统计,如果设置12个选餐窗口,4个套餐窗口,4个面食窗口,就餐高峰期时,假设大家在排队时自动选择较短的队伍等待(即各类餐食的窗口前队伍长度各自相同),求选择选餐的同学取到午餐的最长等待时间;
(2)取餐时至多等待多长时间能让的同学感到满意?(即在接受等待时长内取到餐,保留整数);
(3)根据以上的调查统计,从等待时长和公平的角度上考虑,如何设置各类售饭窗口数更优化,并给出你的求解过程.
17.(15分)如图,在四边形ABCD中,,且,若P,Q为线段AD上的两个动点,且.
(1)当为AD的中点时,求CP的长度;
(2)求的最小值.
18.(17分)如图,在正三棱柱中,为的中点.
(1)证明:平面.
(2)求异面直线与所成角的余弦值.
(3)在上是否存在点,使得平面平面?若存在,求出的值;若不存在,说明理由.
19.(17分)在①,②,③这三个条件中任选一个,补充在下面的问题中,并解答该问题.
在 中,内角的对边分别是,且满足_______,.
(1)若,求的面积;
(2)求周长的取值范围.
数学·参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】A
【解析】在中,由正弦定理可得:,
由,可得:,
所以,因为,所以,
即,所以,
因为,所以,
所以,所以为直角三角形,
故“”是“为直角三角形”的充分条件;
若为直角三角形,设,,
则,所以,
所以,
所以“”不是“为直角三角形”的必要条件;
即“”是“为直角三角形”的充分不必要条件.
故选:A.
2.【答案】B
【解析】∵,
∴,∴;
,∴;
,∴,
∴.
故选:B.
3.【答案】C
【解析】作出函数的图象,如图所示:
将原问题转化为直线(过定点)与函数的图象交点的个数,由图可知,当时,直线与函数的图象只有一个交点;
当时,直线与函数的图象没有交点;
当时,直线与函数的图象有三个交点;
所以直线与函数的图象不可能有两个交点.
故选:C.
4.【答案】D
【解析】至少要用8根小木棍的对立事件为用5根,6根,7根这三种情况.
用5根小木棍为1,2,6这一种情况,组成三位数包括6个样本点,
用6根有1,2,3;1,2,7;1,6,3;1,6,7这四种情况,每种情况包含6个样本点,共24个样本点
用7根有1,2,4;1,2,8;1,6,4;1,6,8;1,3,7;2,6,7;2,6,3这七种情况,
每种情况包含6个样本点,共42个样本点
又表示一个不含“0”且没有重复数字的三位数有504种情况
故至少要用8根小木棍的概率为1-,
故选:D.
5.【答案】C
【解析】圆锥轴截面如图所示,
设圆柱的底面半径为 , ,由 可知, ,即 ,所以 ,
故被挖去的圆柱的侧面积为 ,
当且仅当 时取等号,即 时,被挖去的圆柱的侧面积最大值为 .
故选:C
6.【答案】A
【解析】由正弦定理可得 ,设 ,则 ,解得 ,故 的三边长分别是 .设 的内切圆的半径是 ,则 ,所以 .
7.【答案】C
【解析】由题可知,
由,则,
由,则,,
则
,
故有,故,故,即,
则,由,则,
故.
故选:C.
8.【答案】B
【解析】因为,所以,
整理可得,即有.
又,所以,解得,所以,
于是.
因为三角形是锐角三角形,所以,所以,
所以的取值范围是.
故选B.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分,若只有2个正确选项,每选对1个得3分;若只有3个正确选项,每选对1个得2分.
9.【答案】BC
【解析】对于A:样本相关系数r的绝对值越大,两个变量的线性相关程度越强;反之,线性相关程度越弱,故A错误;
对于B:将数据按升序排列可得:21,29,30,32,38,49,50,65,
因为样本数据有8个,且,
所以第60百分位数为第5位数38,故B正确;
对于C:因为,且,则,
所以,故C正确;
对于D:新样本即对原样本剔除最大值和最小值,
可得新样本的波动性减小,
所以的标准差不大于的标准差,故D错误;
故选BC.
10.【答案】BCD
【解析】因为为上的增函数,所以.
因为函数在上有增有减,所以A中的不等式不恒成立,A错误;
因为函数在上单调递减,
所以当,,时,,故B正确;
因为在上单调递增,所以当时,,故C正确;
因为函数在上单调递增,
所以当,,时,,故D正确.
故选:BCD.
11.【答案】AC
【解析】如图:
由双曲线的标准方程,可知,,所以,所以双曲线的焦距为:,故A正确;
双曲线的渐近线为,即,点到渐近线的距离为:
,故B错误;
设双曲线的左焦点为,根据双曲线的定义:,
所以,故C正确;
在中,由,,,
由余弦定理得:,
所以,
所以,所以,故D错误.
故选:AC
三、填空题:本大题共3个小题,每小题5分,共15分.
12.【答案】6
【解析】函数的图像抛物线开口向上,对称轴方程为,
则,解得,
所以在上单调递增,所以即
所以为方程的两个根,即为方程的两个根,
由韦达定理有.
故答案为:6.
13.【答案】
【解析】由图可知,,即,
则解得,,故.
则,最小正周期为.
直线()与这部分图象相交于三个点,横坐标从左到右分别为,,,则由图可知,.
所以
.
14.【答案】
【解析】解:由题意,,
则由正弦定理可得,
∵,∴,∴,
又∵,则,
∴,
∴.又由,
可得:,则,
∴,即,则,
∴,即,由解得:,
∴由解得:,.
∴由正弦定理可得:,解得:,,
∴.
故答案为:
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)【答案】(1);(2).
【解析】(1)因为的定义域为,,
所以,即恒成立,
因为,,当时等号成立,
所以,即的取值范围为;
(2)因为函数在其定义域上为增函数,要使在区间上单调递增,则函数在区间上单调递增,又为增函数,
所以在上为增函数,显然时不合题意,
所以,且,
又在区间上单调递增,且值域为,
所以,即,
所以在上有两个不等实根,
则,解得,
所以的取值范围为.
16.(15分)【答案】(1)20分钟;(2)18分钟;(3)答案见解析
【解析】(1)由题意得就餐高峰期时选择选餐的总人数为人;这120人平均分布在12个选餐窗口,平均每个窗口等待就餐的人数为人,所以选择选餐的同学取到午餐的最长等待时间为分钟,
(2)由可接受等待时长的频率分布直方图可知,
分组为的频率分别为,
所以可接受等待时长在分钟以内的同学占0.05,即有的同学不满意
可接受等待时长在分钟以内的同学占,
即有的同学对等待时间少于15分钟感到满意,
所以至多等待的时间,能让的同学感到满意
,所以分钟,
至多等待18分钟,能让的同学感到满意.
(3)假设设置个选餐窗口,个套餐窗口,个面食窗口,
则各队伍的同学最长等待时间如下:
类别 选餐 套餐 面食
高峰期就餐总人数 120 72 48
各队伍长度(人)
最长等待时间(分钟)
依题意,从等待时长和公平的角度上考虑,则要求每个队伍的最长等待时间大致相同,即得,即有,
而,故,
因此建议设置选餐 套餐 面食三个类别的窗口数分别为15,2,3个.
17.(15分)【答案】(1);(2)
【解析】(1)由,得,
因为,所以,
又,
所以;
(2)设,,
则,
,
所以
,
当时,取到最小值,且为.
18.(17分)【答案】(1)证明见解析;(2);(3)存在,
【解析】(1)由正三棱柱的定义可知是等边三角形,平面.
因为平面,所以.
因为是等边三角形,D为的中点,所以.
因为,平面,且,
所以平面.
(2)如图,取的中点,连接,,则,
则是异面直线与CD所成的角或补角.
设,则,,,,
故,
即异面直线与CD所成角的余弦值为.
(3)在中,作,垂足为E.
因为平面,且平面,
所以.
因为平面,且,
所以平面.
因为平面BCE,所以平面平面.
设,则,,故.
因为,
所以,
则,,
所以.
故在上存在点E,使得平面平面,此时.
19.(17分)【答案】(1)任选一条件,面积皆为;(2).
【解析】(1)若选条件①, 由 及正弦定理, 得
即 , 化简得,
因为, 所以, 所以,因为 , 所以.
若选条件②, 由 及正弦定理, 得, 即, 化简得,
因为 , 所以, 所以,因为 , 所以.
若选条件③, 由 化简得,, 由余弦定理得, 即,因为 , 所以,
所以三个条件,都能得到.
由余弦定理得 , 即, 解得,
所以的面积.
(2)因为 , 由正弦定理得,
因为 ,
所以 ,
因为 , 所以,
所以 , 即, 所以周长的取值范围为.
第 page number 页,共 number of pages 页
同课章节目录
