河南省驻马店市新蔡县新蔡县第一高级中学2023-2024学年高一下学期7月月考数学试题(含答案)
文档属性
| 名称 | 河南省驻马店市新蔡县新蔡县第一高级中学2023-2024学年高一下学期7月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 861.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 17:45:18 | ||
图片预览



文档简介
新蔡县第一高级中学2023-2024学年高一下学期7月月考数学试题
一、选择题:本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.已知复数满足,则的虚部为( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.已知向量,则下列选项中与共线的单位向量是( )
A. B.
C. D.
4.我们学过度量角有角度制与弧度制,最近,有学者提出用“面度制”度量角,因为在半径不同的同心圆中,同样的圆心角所对扇形的面积与半径平方之比是常数,从而称这个常数为该角的面度数,这种用面度作为单位来度量角的单位制,叫做面度制.在面度制下,角的面度数为,则角的正弦值为( )
A. B. C. D.
5.已知是两个不同的平面,是两条不同的直线,下列说法正确的是( )
A.若上有两点到平面距离相等,则
B.若,则与是异面直线
C.若,则与没有公共点
D.若,则与一定相交
6.已知,是函数的零点,则( )
A. B. C. D.
7.已知函数,则下列说法正确的是( )
A.函数的图象可以由的图象向右平移个单位,再向上平移1个单位得到
B.函数是偶函数
C.函数的图象关于点对称
D.函数的最小正周期为
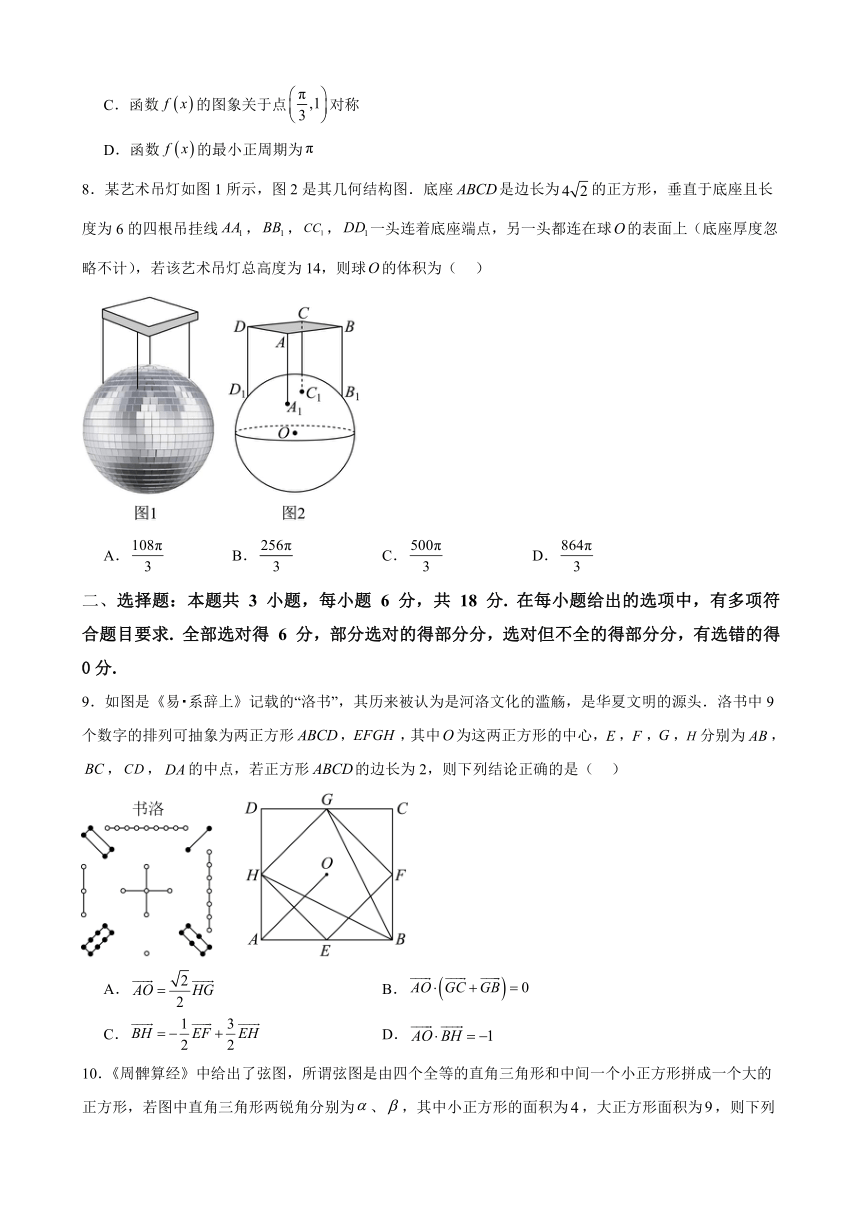
8.某艺术吊灯如图1所示,图2是其几何结构图.底座是边长为的正方形,垂直于底座且长度为6的四根吊挂线,,,一头连着底座端点,另一头都连在球的表面上(底座厚度忽略不计),若该艺术吊灯总高度为14,则球的体积为( )
A. B. C. D.
二、选择题:本题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的选项中,有多项符合题目要求. 全部选对得 6 分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.
9.如图是《易 系辞上》记载的“洛书”,其历来被认为是河洛文化的滥觞,是华夏文明的源头.洛书中9个数字的排列可抽象为两正方形,,其中为这两正方形的中心,,,,分别为,,,的中点,若正方形的边长为2,则下列结论正确的是( )
A. B.
C. D.
10.《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为、,其中小正方形的面积为,大正方形面积为,则下列说法正确的是( )
A.每一个直角三角形的面积为 B.
C. D.
11.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”.如图,在堑堵中,,且,过点分别作于点于点,则下列结论正确的是( )
A.四棱锥为“阳马” B.直线AE与平面ABC所成的角为
C. D.堑堵的外接球的体积为
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12.在中,角的对边分别为且若三角形的面积为且则 .
13.已知中,,,,则在方向上的数量投影为 .
14.早在公元5世纪,我国数学家祖暅就提出:“幂势既同,则积不容异”.如图,抛物线C的方程为,过点(1,0)作抛物线C的切线l(l的斜率不为0),将抛物线C、直线l及x轴围成的阴影部分绕y轴旋转一周,所得的几何体记作,利用祖暅原理,可得出几何体的体积为 .
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15.(1)已知,,求的值.
(2)设为正实数,已知,
求①的值;②的值.
16.锐角中角、、的对边分别为、、,且.
(1)求角的大小;
(2)若,求的取值范围.
17.在中,内角A,B,C的对边分别为a,b,c,BC,AC边上的两条中线AM,BN相交于点P.
(1)令,,用,表示;
(2)证明:;
(3)若,,,求∠MPN的余弦值.
18.如图1,在矩形中,点在边上,,将沿进行翻折,翻折后点到达点位置,且满足平面平面,如图2.
(1)若点在棱上,平面,求证:;
(2)求点到平面的距离.
19.某游乐场的摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点),在旋转过程中,座舱与地面的距离h与时间t的函数关系基本符合正弦函数模型,现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为t分钟.
(1)求1号座舱与地面的距离h与时间t的函数关系的解析式;
(2)在前24分钟内,求1号座舱与地面的距离为17米时t的值;
(3)记1号座舱与5号座舱高度之差的绝对值为H米,求当H取得最大值时t的值.
参考答案:
1.B2.B3.B4.D5.C6.B7.C8.C
9.BCD10.ACD11.ACD
12. 13. 14.
15.(1)由,得,即,
则,由,得,则,
所以.
(2)①正实数满足:,两边平方得,所以;
②,由①知,,两边平方得,所以.
16.(1)由正弦定理可得,即,
由余弦定理可得,又,则;
(2)由,则、,
则
,
由为锐角三角形,可得,解得,
则,则,故.
17.(1)由题可知是的重心,且,所以.
(2)在中,由余弦定理,得,
在中,由余弦定理,得
.
(3)因为,,,
所以,
所以,即的余弦值为.
18.(1)因为,平面,平面,
所以平面,
又平面,平面,所以平面平面,
平面,所以.
(2)取的中点,连接,依题意,所以且,
又平面平面,平面平面,平面,
所以平面,
连接、,则,所以,
又,,,,
所以
,
又平面,平面,所以,
所以,
则,
则,
所以,
设点到平面的距离为,则,
解得,即点到平面的距离为.
19.(1)设1号座舱与地面的距离h与时间t的函数关系的解析式为
则,
∴,
依题意,∴,
当时,∴,∴.
(2)令,即,∴,
∵,∴,∴或,
解得或,
∴或时,1号座舱与地面的距离为17米.
(3)依题意,
∴
令,解得,所以当时,H取得最大值
一、选择题:本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.已知复数满足,则的虚部为( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.已知向量,则下列选项中与共线的单位向量是( )
A. B.
C. D.
4.我们学过度量角有角度制与弧度制,最近,有学者提出用“面度制”度量角,因为在半径不同的同心圆中,同样的圆心角所对扇形的面积与半径平方之比是常数,从而称这个常数为该角的面度数,这种用面度作为单位来度量角的单位制,叫做面度制.在面度制下,角的面度数为,则角的正弦值为( )
A. B. C. D.
5.已知是两个不同的平面,是两条不同的直线,下列说法正确的是( )
A.若上有两点到平面距离相等,则
B.若,则与是异面直线
C.若,则与没有公共点
D.若,则与一定相交
6.已知,是函数的零点,则( )
A. B. C. D.
7.已知函数,则下列说法正确的是( )
A.函数的图象可以由的图象向右平移个单位,再向上平移1个单位得到
B.函数是偶函数
C.函数的图象关于点对称
D.函数的最小正周期为
8.某艺术吊灯如图1所示,图2是其几何结构图.底座是边长为的正方形,垂直于底座且长度为6的四根吊挂线,,,一头连着底座端点,另一头都连在球的表面上(底座厚度忽略不计),若该艺术吊灯总高度为14,则球的体积为( )
A. B. C. D.
二、选择题:本题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的选项中,有多项符合题目要求. 全部选对得 6 分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.
9.如图是《易 系辞上》记载的“洛书”,其历来被认为是河洛文化的滥觞,是华夏文明的源头.洛书中9个数字的排列可抽象为两正方形,,其中为这两正方形的中心,,,,分别为,,,的中点,若正方形的边长为2,则下列结论正确的是( )
A. B.
C. D.
10.《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为、,其中小正方形的面积为,大正方形面积为,则下列说法正确的是( )
A.每一个直角三角形的面积为 B.
C. D.
11.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”.如图,在堑堵中,,且,过点分别作于点于点,则下列结论正确的是( )
A.四棱锥为“阳马” B.直线AE与平面ABC所成的角为
C. D.堑堵的外接球的体积为
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12.在中,角的对边分别为且若三角形的面积为且则 .
13.已知中,,,,则在方向上的数量投影为 .
14.早在公元5世纪,我国数学家祖暅就提出:“幂势既同,则积不容异”.如图,抛物线C的方程为,过点(1,0)作抛物线C的切线l(l的斜率不为0),将抛物线C、直线l及x轴围成的阴影部分绕y轴旋转一周,所得的几何体记作,利用祖暅原理,可得出几何体的体积为 .
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15.(1)已知,,求的值.
(2)设为正实数,已知,
求①的值;②的值.
16.锐角中角、、的对边分别为、、,且.
(1)求角的大小;
(2)若,求的取值范围.
17.在中,内角A,B,C的对边分别为a,b,c,BC,AC边上的两条中线AM,BN相交于点P.
(1)令,,用,表示;
(2)证明:;
(3)若,,,求∠MPN的余弦值.
18.如图1,在矩形中,点在边上,,将沿进行翻折,翻折后点到达点位置,且满足平面平面,如图2.
(1)若点在棱上,平面,求证:;
(2)求点到平面的距离.
19.某游乐场的摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点),在旋转过程中,座舱与地面的距离h与时间t的函数关系基本符合正弦函数模型,现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为t分钟.
(1)求1号座舱与地面的距离h与时间t的函数关系的解析式;
(2)在前24分钟内,求1号座舱与地面的距离为17米时t的值;
(3)记1号座舱与5号座舱高度之差的绝对值为H米,求当H取得最大值时t的值.
参考答案:
1.B2.B3.B4.D5.C6.B7.C8.C
9.BCD10.ACD11.ACD
12. 13. 14.
15.(1)由,得,即,
则,由,得,则,
所以.
(2)①正实数满足:,两边平方得,所以;
②,由①知,,两边平方得,所以.
16.(1)由正弦定理可得,即,
由余弦定理可得,又,则;
(2)由,则、,
则
,
由为锐角三角形,可得,解得,
则,则,故.
17.(1)由题可知是的重心,且,所以.
(2)在中,由余弦定理,得,
在中,由余弦定理,得
.
(3)因为,,,
所以,
所以,即的余弦值为.
18.(1)因为,平面,平面,
所以平面,
又平面,平面,所以平面平面,
平面,所以.
(2)取的中点,连接,依题意,所以且,
又平面平面,平面平面,平面,
所以平面,
连接、,则,所以,
又,,,,
所以
,
又平面,平面,所以,
所以,
则,
则,
所以,
设点到平面的距离为,则,
解得,即点到平面的距离为.
19.(1)设1号座舱与地面的距离h与时间t的函数关系的解析式为
则,
∴,
依题意,∴,
当时,∴,∴.
(2)令,即,∴,
∵,∴,∴或,
解得或,
∴或时,1号座舱与地面的距离为17米.
(3)依题意,
∴
令,解得,所以当时,H取得最大值
同课章节目录
