3.3正方形的性质与判定（1）

课件25张PPT。初中数学九年级 上册
(苏科版)
第一章 第三节
平行四边形、矩形、菱形、
正方形的性质与判定（1）
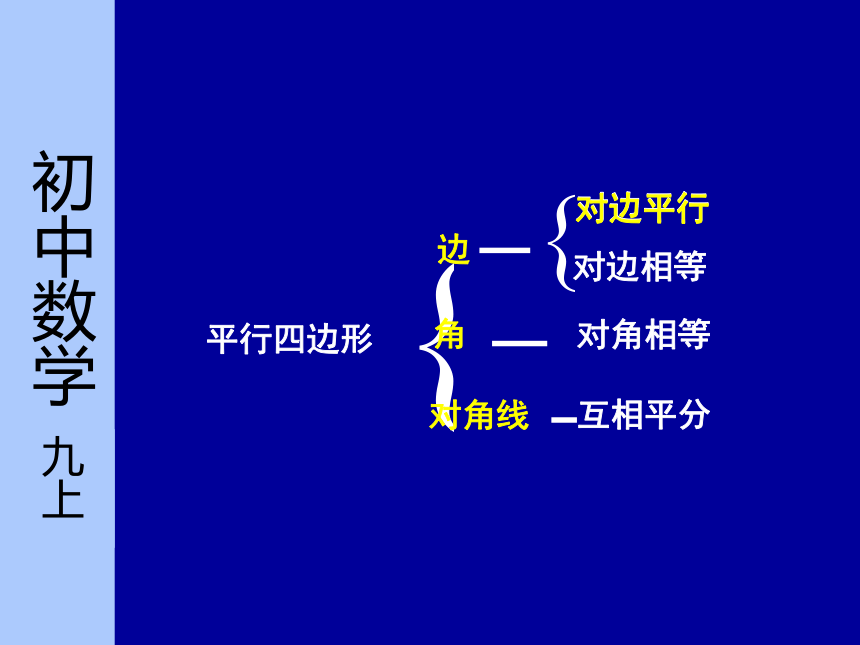
　平行四边形对边平行边角对角线对边相等对角相等互相平分对边平行平行四边形的对边相等;
平行四边形的对角相等;
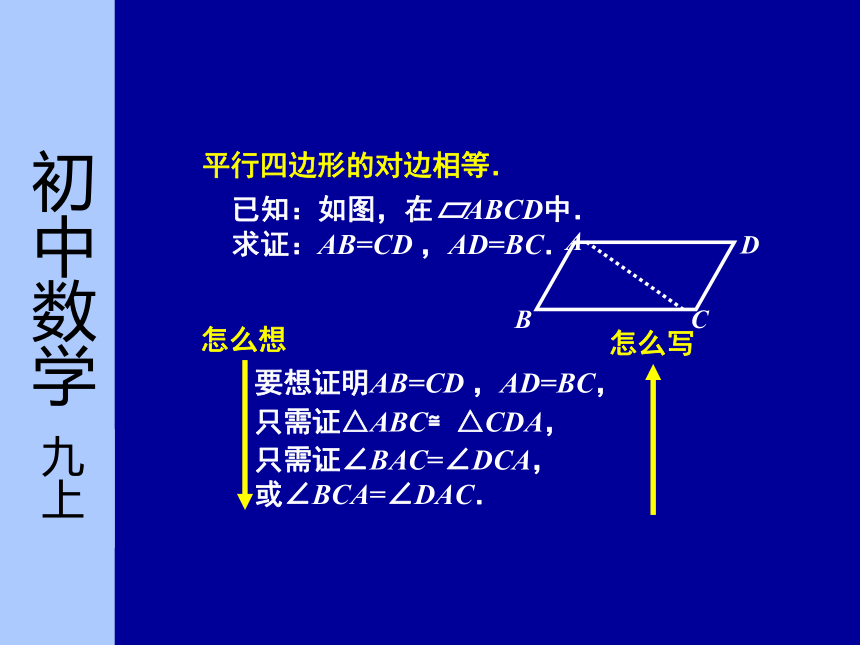
平行四边形的对角线互相平分．要想证明AB=CD ，AD=BC，只需证∠BAC=∠DCA，
或∠BCA=∠DAC．只需证△ABC≌△CDA， 已知：如图，在 ABCD中．
求证：AB=CD ，AD=BC．　　平行四边形的对边相等．证明：连结AC.
∵四边形ABCD是平行四边形，
∴ AB∥CD ，AD∥BC．
∴ ∠BAC=∠DCA，∠BCA=∠DAC．
在△ABC 和△CDA 中，
∠BAC=∠DCA (已证)，
AC=CA (公共边)，
∠BCA=∠DAC (已证) ．
∴△ABC≌△CDA (ASA)．
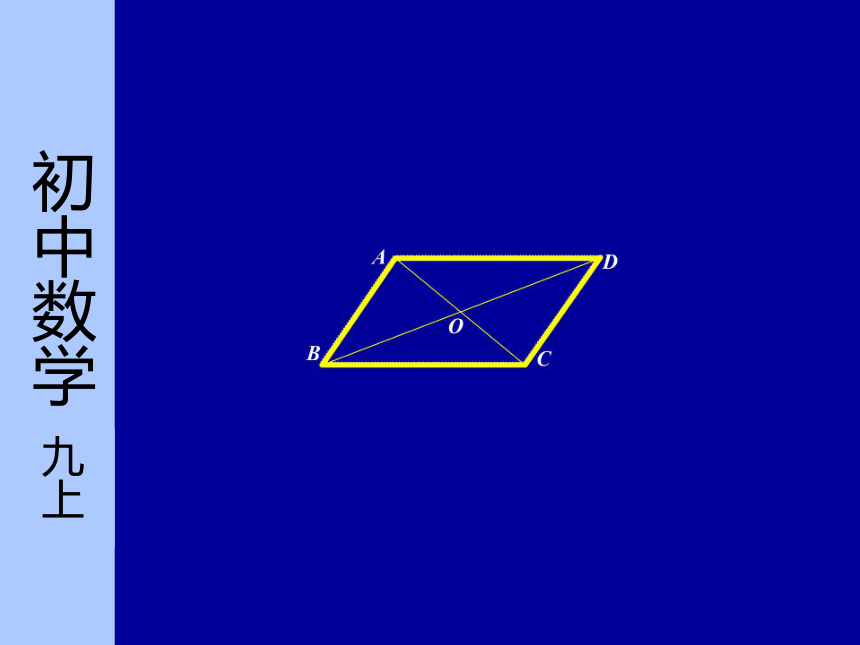
∴AB=CD ，AD=BC(全等三角形的对应边相等) ． 已知：如图，在　ABCD中．
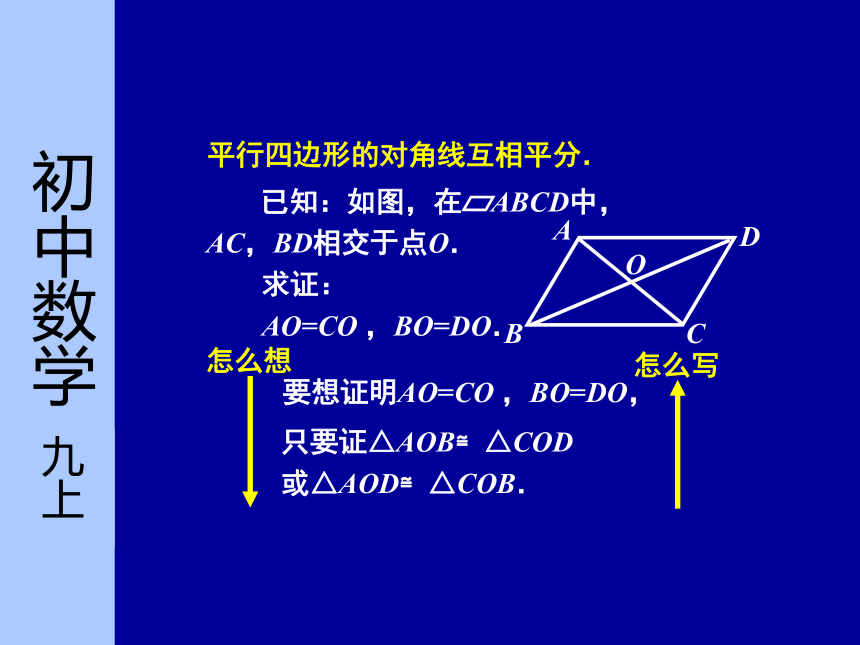
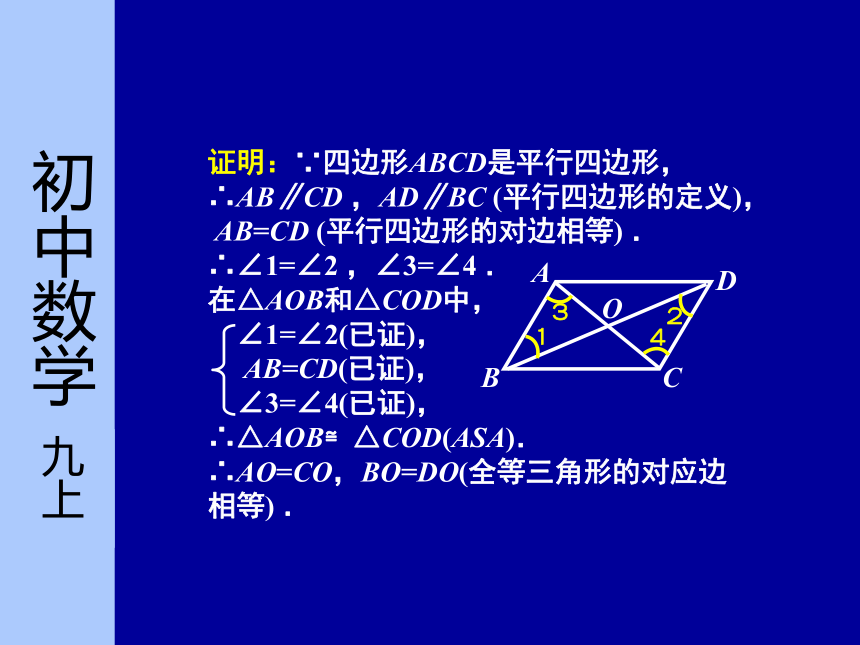
求证：AB=CD ，AD=BC．　定理 平行四边形的对角相等.定理 平行四边形的对边相等.平行四边形的对角线互相平分．要想证明AO=CO ，BO=DO，只要证△AOB≌△COD或△AOD≌△COB．证明：∵四边形ABCD是平行四边形，
∴AB∥CD ，AD∥BC (平行四边形的定义)，
AB=CD (平行四边形的对边相等) ．
∴∠1=∠2 ，∠3=∠4 ．
在△AOB和△COD中，
　∠1=∠2(已证)，
　AB=CD(已证)，
　∠3=∠4(已证)，
∴△AOB≌△COD(ASA)．
∴AO=CO，BO=DO(全等三角形的对应边
相等) ．定理 平行四边形的对角线互相平分． 　　定理 平行四边形的对角相等．定理 平行四边形的对边相等．证明：∵四边形ABCD是平行四边形，
∴ AB∥CD ，AD∥BC．
∴ ∠B+∠C=180°， ∠A+∠B=180°．
∴ ∠A=∠C．
同理可得，∠B=∠D． 已知：如图，在　ABCD中， AC，BD 相交于点O．
求证：AO=CO ，BO=DO．　要想证明AO=CO ，BO=DO，只需证AB=CD，只要证△AOB≌△COD，只需证△ABC≌△CDA．证明：∵四边形ABCD是平行四边形，
∴AB∥CD ，AD∥BC ．
∴∠1=∠2 ，∠3=∠4 ．
在△ABC和△CDA中，
∠1=∠2(已证)，
AC=CA(公共边)，
∠3=∠4(已证)，
∴△ABC≌△CDA(ASA)
∴ (全等三角形的对应边相等) ．AB=CD 在△AOB和△COD中，
∠1=∠2(已证)，
∠AOB=∠COD(对顶角相等)，
AB=CD(已证)，
∴△AOB≌△COD(AAS)．
∴AO=CO，BO=DO(全等三角形的对应边相等) ．证明：∵四边形ABCD是平行四边形，
∴AB∥CD ，AD∥BC ．
∴∠1=∠2 ，∠3=∠4 ．
在△ABC和△CDA中，
∠1=∠2(已证)，
AC=CA(公共边)，
∠3=∠4(已证)，
∴△ABC≌△CDA(ASA)
∴ (全等三角形的对应边相等) ．AB=CD AB=CD 要证BE=DF，
只需证△ABE≌△CDF．
只需证AB =CD，AE =CF．
∠A=∠C．　　已知：如图，在 ABCD中，E，F分
别是AD，BC的中点． 　　　　　　　　　　　　　　　 　　　　　　　　　　　　
　　求证：BE=DF．例题证明：∵四边形ABCD是平行四边形，
∴∠A=∠C (平行四边形的对角相等)，
AB=CD， AD=BC (平行四边形的对边相等) ．
∵Ｅ，F分别是AD，BC的中点，
∴ AE= AD， CF= BC．
∴ AE=CF．
∴△ABE≌△CDF(SAS)．
∴BE=DF(全等三角形的对应边相等) ．拓展一CＡＢD　　如果AE= AD，CF= BC，BE与DF
相等吗?　　如果AE= AD，CF= BC，BE与DF
相等吗?　　如果AE= AD，CF= BC，BE与DF
相等吗?　　已知：如图，在 ABCD中，
　　　　　　　　　　　　　　　 　　　　　　　　　　　　
　　求证：BE=DF．拓展二CＡＢD　BE∥DF．　　　　　　　　　　　　　　　E，F分
别是AD，BC的中点．　证明：∵四边形ABCD是平行四边形，
∴AB∥CD (平行四边形的定义)．
∵BE∥DF，
∴四边形BEDF是平行四边形
(平行四边形的定义) ．
∴BE=DF(平行四边形的对边相等) ．　　已知：如图，直线a∥b，AB∥CD． 　　　　　　　　　　　　　　　 　　　　　　　　　　　　
　　求证：AB=CD．拓展三得出结论：
夹在两条平行线间的平行线段相等．　　已知：如图，直线a∥b，AB∥CD∥EF ． 　　　　　　　　　　　　　　　 　　　　　　　　　　　　
　　求证：AB=CD=EF．一试身手　　　　已知：如图， ABCD的对角线AC，BD相交于点O，过点O的直线与AD，BC分别相交于点E，F．
　　求证：OE=OF．要证OE =OF，
只需证△AOE≌△COF
或△DOE≌△BOF ．
只需找两个三角形全等的条件．证明：∵四边形ABCD是平行四边形，
∴OA=OC (平行四边形的对角线互相平分)，
AD∥BC(平行四边形的定义)．
∴∠OAE=∠OCF．
在△AOE 和△COF中，
∠OAE=∠OCF (已证)，
AO=OC(已证)，
∠AOE=∠COF(对顶角相等) ，
∴△AOE≌△COF (ASA)．
∴OE=OF(全等三角形的对应边相等) ．　　已知：如图， ABCD的对角线AC，BD
相交于点O，过点O的直线与AD，BC分别相交于点E，F．
　　求证：OE=OF．　　已知：如图， ABCD的对角线AC，BD
相交于点O，过点O的直线与BA，DC的延长线分别相交于点E，F．
　　求证：OE=OF．一试身手　　学有所获　　研究四边形问题常用的思考方法——
将四边形问题转化为三角形问题．