数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 21:45:16 | ||
图片预览











文档简介
(共30张PPT)
新授课
1.1.1 空间向量及其线性运算
第一章 空间向量与立体几何
上个学期,我们学习了向量在平面中的应用,那么向量在空间中又有怎样的理解呢
情境导入
图1 线缆同时受到来
自不同方向的支持力
图2 跳伞运动员同时受到
重力、风力、绳索牵拉力
新知探究
1.空间向量定义:如图,与平面向量一样,在空间中我们把具有大小和方向的量叫做空间向量.
2.长度或模:空间向量的大小叫做空间向量的长度或模.
3.表示方法
(1)符号表示:例如 空间向量
(2)几何表示:三条有向线段表示的三个向量为
4.零向量:与平面向量一样,我们规定,长度为0的向量叫做零向量,
记作 0(或 ).
5.单位向量:模为1的向量叫做单位向量,
通常用 表示,即 .
注:任何一个非零向量 都有它的单位向量,
且
几类特殊的空间向量
几类特殊的空间向量
6.相等向量
方向相同且模相等的向量叫做相等向量 . 如图 向量为相等向量,记作 .
空间向量具有平移不变性.
7.相反向量
如图,与向量 长度相等且方向相反的向量叫做 的相反向量,记作 .
8.共线向量(或平行向量)
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
规定:零向量与任意向量平行,即对于任意向量 ,都有 .
共线向量(或平行向量)
几类特殊的空间向量
辨析.判断正误.
(1)空间两个向量方向相反时,它们互为相反向量( )
(2)若空间两个向量相等,则它们方向相同,且起点相同( )
(3)若空间两个向量起点相同且长度相等,则这两个向量相等( )
(4)将空间所有单位向量平移到同一个起点,则它们的终点构成一个圆( )
× × × ×
[例1] (多选)下列命题中错误的是 ( )
A.若两个空间向量相等,则它们的起点相同,终点也相同
B.若空间向量a,b满足|a|=|b|,则a=±b
C.空间中任意两个单位向量必相等
D.在如图所示的正方体AC1中,必有=
[答案] ABC
新知探究
思考:空间向量是如何运算的呢?与平面向量的运算有什么关系吗?
a
b
a
b
O
A
B
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,这样任意两个空间向量的运算,都可以转化为平面向量的运算.
空间向量的运算法则
9. 空间向量的加减运算
A
B
C
O
一般地,我们规定实数 与向量 的积是一个向量,这种运算叫做向量的数乘,记作 ,它的长度与方向规定如下:
(1) 的长度为:
(2) 的方向为:
①当时, 的方向与的方向相同;
②当 时, 的方向与的方向相反;
③当 时,=.
10、空间向量的数乘运算
与平面向量一样,空间向量的线性运算满足以下运算律(其中):
交换律:
结合律:
分配律:
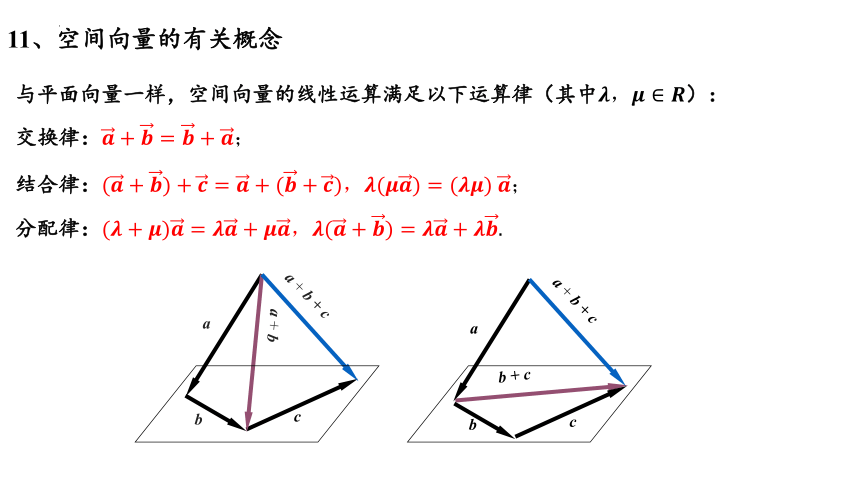
11、空间向量的有关概念
b
c
a
a + b + c
a + b
b
a
a + b + c
b + c
c
练一练:如图,已知平行六面体,化简下列向量表达式,并标出化简结果的向量.
A
B
C
D
A1
B1
C1
D1
(1)
(2)
(3)
(4)
练一练:已知空间四边形中,向量 , ,若为的中点,为的重心,试用, , 表示下列向量:
(1) ; (2) .
A
M
C
G
D
B
共线向量定理:对任意两个空间向量,,的充要条件是存在实数,使.
探究共线向量定理
例3 (1)已知空间向量a,b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是 ( )
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D
(2)若非零空间向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为 .
探究方向向量
是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.我们把与向量平行的非零向量称为直线的方向向量
P
注1:与直线平行的任意非零向量 都叫做直线的非零向量;
注2:因为的方向是任意的,所以 不能作为直线的方向向量.
探究共面向量
平面向量基本定理:
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
参考上述定理,思考共面向量的定理?
O
A
B
共面向量:
因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
如图,已知空间向量,以任意点〇为起点,作向量 ,我们就可以把它们平移到同一个平面内.
注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,也可能不共面.
d
b
a
c
共面向量:平行于同一平面的向量,叫做共面向量.
三个空间向量共线的充要条件
由平面向量基本定理可知,
如果空间中两个向量 , 不共线,那么向量 与向量 ,共面的充要条件是存在唯一的有序实数对,使
与不共线向量,共面
例4:如图,已知平行四边形,过平面外一点作射线,,,,在四条射线上分别取点,,,,使.
求证:,,,四点共面.
证明:因为,
所以
因为四边形是平行四边形,所以
因此
由向量共面的充要条件可知,,共面,又
过同一点,从而,,,四点共面.
、、三点共线
、、、 点共面
练习1:已知为空间任意一点,,,,四点共面,但任意三点不共线,如果,则的值为____________
【答案】
,
因为为空间任意一点,满足任意三点不共线,且四点共面,
所以,故.
练习2:在空间四边形OABC中,M为OA中点,N为BC的中点,
若 ,则使G、M、N三点共线的x的值是 .
练习3:已知点在确定的平面内,是平面外任意一点,实数满足,则的最小值为________
课堂小结
1、空间向量的相关概念
2、空间向量的线性运算
3、空间向量的共线、共面的表示
新授课
1.1.1 空间向量及其线性运算
第一章 空间向量与立体几何
上个学期,我们学习了向量在平面中的应用,那么向量在空间中又有怎样的理解呢
情境导入
图1 线缆同时受到来
自不同方向的支持力
图2 跳伞运动员同时受到
重力、风力、绳索牵拉力
新知探究
1.空间向量定义:如图,与平面向量一样,在空间中我们把具有大小和方向的量叫做空间向量.
2.长度或模:空间向量的大小叫做空间向量的长度或模.
3.表示方法
(1)符号表示:例如 空间向量
(2)几何表示:三条有向线段表示的三个向量为
4.零向量:与平面向量一样,我们规定,长度为0的向量叫做零向量,
记作 0(或 ).
5.单位向量:模为1的向量叫做单位向量,
通常用 表示,即 .
注:任何一个非零向量 都有它的单位向量,
且
几类特殊的空间向量
几类特殊的空间向量
6.相等向量
方向相同且模相等的向量叫做相等向量 . 如图 向量为相等向量,记作 .
空间向量具有平移不变性.
7.相反向量
如图,与向量 长度相等且方向相反的向量叫做 的相反向量,记作 .
8.共线向量(或平行向量)
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
规定:零向量与任意向量平行,即对于任意向量 ,都有 .
共线向量(或平行向量)
几类特殊的空间向量
辨析.判断正误.
(1)空间两个向量方向相反时,它们互为相反向量( )
(2)若空间两个向量相等,则它们方向相同,且起点相同( )
(3)若空间两个向量起点相同且长度相等,则这两个向量相等( )
(4)将空间所有单位向量平移到同一个起点,则它们的终点构成一个圆( )
× × × ×
[例1] (多选)下列命题中错误的是 ( )
A.若两个空间向量相等,则它们的起点相同,终点也相同
B.若空间向量a,b满足|a|=|b|,则a=±b
C.空间中任意两个单位向量必相等
D.在如图所示的正方体AC1中,必有=
[答案] ABC
新知探究
思考:空间向量是如何运算的呢?与平面向量的运算有什么关系吗?
a
b
a
b
O
A
B
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,这样任意两个空间向量的运算,都可以转化为平面向量的运算.
空间向量的运算法则
9. 空间向量的加减运算
A
B
C
O
一般地,我们规定实数 与向量 的积是一个向量,这种运算叫做向量的数乘,记作 ,它的长度与方向规定如下:
(1) 的长度为:
(2) 的方向为:
①当时, 的方向与的方向相同;
②当 时, 的方向与的方向相反;
③当 时,=.
10、空间向量的数乘运算
与平面向量一样,空间向量的线性运算满足以下运算律(其中):
交换律:
结合律:
分配律:
11、空间向量的有关概念
b
c
a
a + b + c
a + b
b
a
a + b + c
b + c
c
练一练:如图,已知平行六面体,化简下列向量表达式,并标出化简结果的向量.
A
B
C
D
A1
B1
C1
D1
(1)
(2)
(3)
(4)
练一练:已知空间四边形中,向量 , ,若为的中点,为的重心,试用, , 表示下列向量:
(1) ; (2) .
A
M
C
G
D
B
共线向量定理:对任意两个空间向量,,的充要条件是存在实数,使.
探究共线向量定理
例3 (1)已知空间向量a,b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是 ( )
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D
(2)若非零空间向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为 .
探究方向向量
是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.我们把与向量平行的非零向量称为直线的方向向量
P
注1:与直线平行的任意非零向量 都叫做直线的非零向量;
注2:因为的方向是任意的,所以 不能作为直线的方向向量.
探究共面向量
平面向量基本定理:
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
参考上述定理,思考共面向量的定理?
O
A
B
共面向量:
因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
如图,已知空间向量,以任意点〇为起点,作向量 ,我们就可以把它们平移到同一个平面内.
注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,也可能不共面.
d
b
a
c
共面向量:平行于同一平面的向量,叫做共面向量.
三个空间向量共线的充要条件
由平面向量基本定理可知,
如果空间中两个向量 , 不共线,那么向量 与向量 ,共面的充要条件是存在唯一的有序实数对,使
与不共线向量,共面
例4:如图,已知平行四边形,过平面外一点作射线,,,,在四条射线上分别取点,,,,使.
求证:,,,四点共面.
证明:因为,
所以
因为四边形是平行四边形,所以
因此
由向量共面的充要条件可知,,共面,又
过同一点,从而,,,四点共面.
、、三点共线
、、、 点共面
练习1:已知为空间任意一点,,,,四点共面,但任意三点不共线,如果,则的值为____________
【答案】
,
因为为空间任意一点,满足任意三点不共线,且四点共面,
所以,故.
练习2:在空间四边形OABC中,M为OA中点,N为BC的中点,
若 ,则使G、M、N三点共线的x的值是 .
练习3:已知点在确定的平面内,是平面外任意一点,实数满足,则的最小值为________
课堂小结
1、空间向量的相关概念
2、空间向量的线性运算
3、空间向量的共线、共面的表示
