2024年中考物理二轮复习压轴题专项练习--机械及其效率(含解析)
文档属性
| 名称 | 2024年中考物理二轮复习压轴题专项练习--机械及其效率(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-09 09:12:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
机械及其效率
讲方法
一、机械类题目的解题思想
1. 杠杆类题目的解题主要分为两步:
第一步:明确杠杆模型并找到杠杆五要素;
第二步:受力分析并根据杠杆平衡原理列出方程,并带入物理量解题.
2. 滑轮类题目的解题主要分为两步:
第一步: 明确滑轮的类型,并确定绳子股数n;
第二步:选定合适的研究对象,对其进行受力分析,并根据滑轮的特点列出方程,然后带入物理量解题.
二、效率类题目的解题思路
1.机械效率一般包括常规 (杠杆、滑轮、斜面等)的机械的机械效率和生活应用类 (起重机、卷扬机等)的机械效率.不管哪种机械的机械效率,我们都需要找到三个关键的物理量:有用功、额外功和总功,在不同的情景中,这三个物理量所对应的表达式不同,我们需要认真分析.
2. 常规情景下的机械效率计算:
(1) 垂直使用滑轮组时 (如图3-4-1甲, 不计绳重及摩擦):
(2)垂直使用滑轮组日物体在液体中时 (如图3-4-1乙, 不计绳重及摩擦):
(3)水平使用滑轮组时 (如图3-4-1丙):
(4)斜面的机械效率 (如图3-4-1丁所示):
学思路
铺垫1
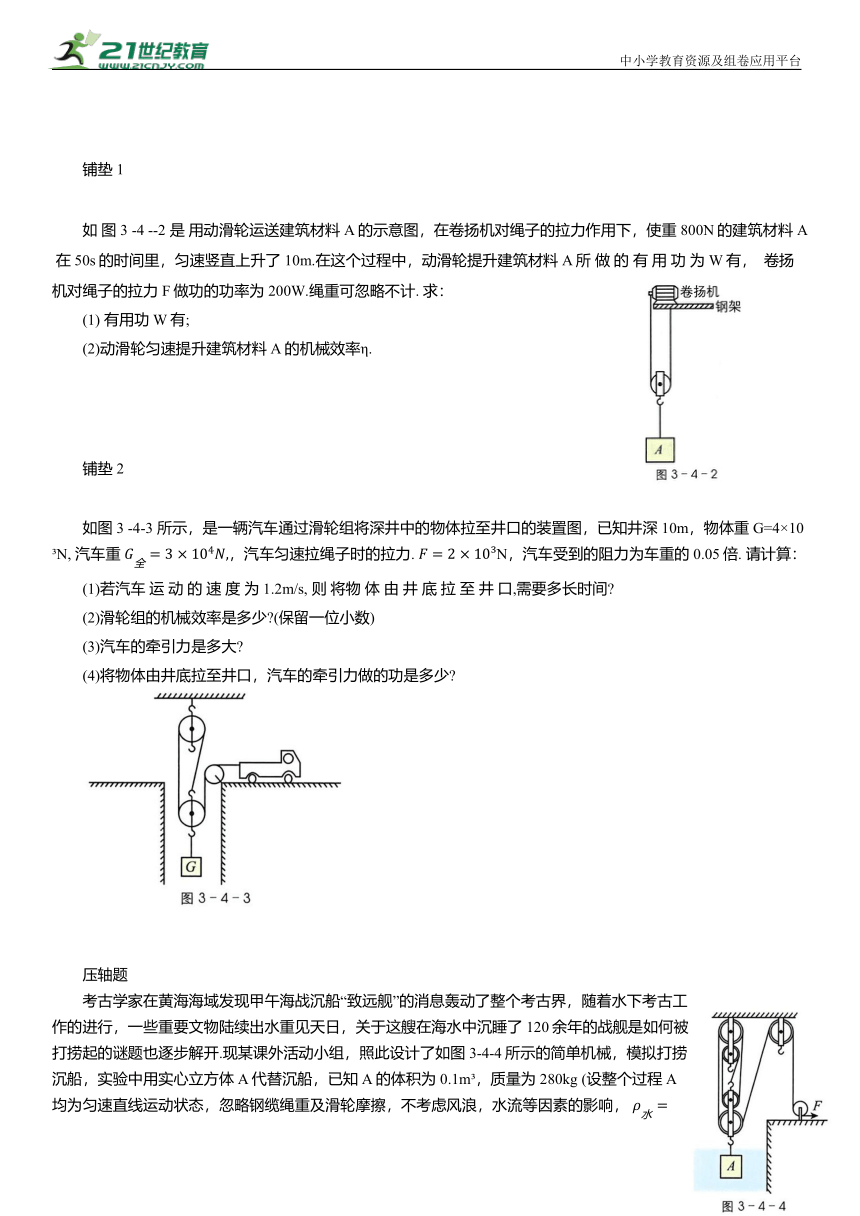
如 图 3 -4 --2 是 用动滑轮运送建筑材料A的示意图,在卷扬机对绳子的拉力作用下,使重 800N的建筑材料 A 在50s的时间里,匀速竖直上升了 10m.在这个过程中,动滑轮提升建筑材料A所 做 的 有 用 功 为 W有, 卷扬机对绳子的拉力 F做功的功率为200W.绳重可忽略不计. 求:
(1) 有用功W有;
(2)动滑轮匀速提升建筑材料A的机械效率η.
铺垫2
如图 3 -4-3 所示,是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图,已知井深 10m,物体重G=4×10 N, 汽车重 ,汽车匀速拉绳子时的拉力. N,汽车受到的阻力为车重的0.05倍. 请计算:
(1)若汽车 运 动 的 速 度 为 1.2m/s, 则 将物 体 由 井 底 拉 至 井 口,需要多长时间
(2)滑轮组的机械效率是多少 (保留一位小数)
(3)汽车的牵引力是多大
(4)将物体由井底拉至井口,汽车的牵引力做的功是多少
压轴题
考古学家在黄海海域发现甲午海战沉船“致远舰”的消息轰动了整个考古界,随着水下考古工作的进行,一些重要文物陆续出水重见天日,关于这艘在海水中沉睡了 120余年的战舰是如何被打捞起的谜题也逐步解开.现某课外活动小组,照此设计了如图3-4-4所示的简单机械,模拟打捞沉船,实验中用实心立方体A代替沉船,已知A的体积为0.1m ,质量为280kg (设整个过程A均为匀速直线运动状态,忽略钢缆绳重及滑轮摩擦,不考虑风浪,水流等因素的影响,
(1)A完全浸没在水中时受到的浮力是多大
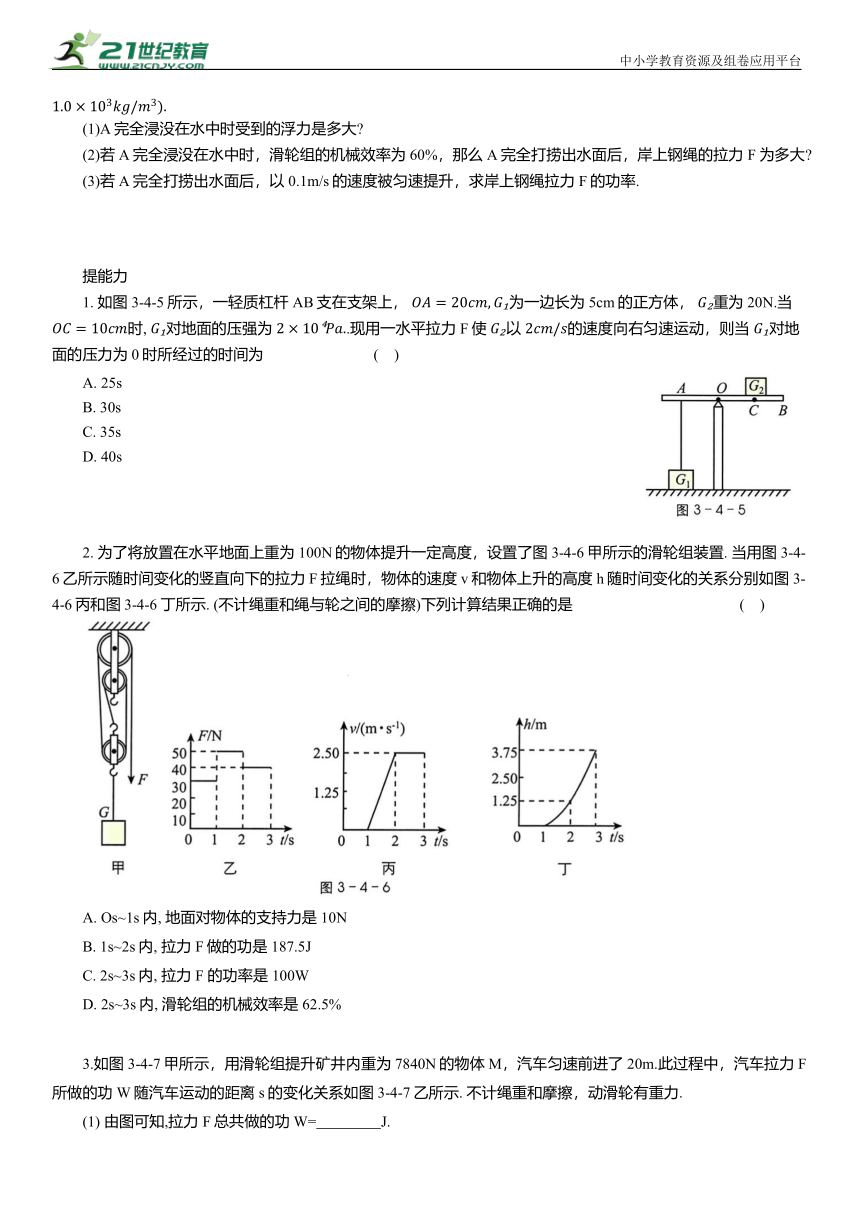
(2)若A完全浸没在水中时,滑轮组的机械效率为60%,那么A完全打捞出水面后,岸上钢绳的拉力 F 为多大
(3)若A完全打捞出水面后,以0.1m/s的速度被匀速提升,求岸上钢绳拉力F的功率.
提能力
1. 如图3-4-5所示,一轻质杠杆AB支在支架上, 为一边长为5cm的正方体, 重为20N.当 时, 对地面的压强为 .现用一水平拉力 F使 以 的速度向右匀速运动,则当 对地面的压力为0时所经过的时间为 ( )
A. 25s
B. 30s
C. 35s
D. 40s
2. 为了将放置在水平地面上重为100N的物体提升一定高度,设置了图3-4-6甲所示的滑轮组装置. 当用图3-4-6乙所示随时间变化的竖直向下的拉力F拉绳时,物体的速度v和物体上升的高度h随时间变化的关系分别如图3-4-6丙和图3-4-6丁所示. (不计绳重和绳与轮之间的摩擦)下列计算结果正确的是 ( )
A. Os~1s内, 地面对物体的支持力是 10N
B. 1s~2s内, 拉力 F做的功是 187.5J
C. 2s~3s内, 拉力 F 的功率是 100W
D. 2s~3s内, 滑轮组的机械效率是62.5%
3.如图3-4-7甲所示,用滑轮组提升矿井内重为7840N的物体M,汽车匀速前进了20m.此过程中,汽车拉力F所做的功W随汽车运动的距离s的变化关系如图3-4-7乙所示. 不计绳重和摩擦,动滑轮有重力.
(1) 由图可知,拉力 F总共做的功W= J.
(2)物体M上升的高度是 m.
(3)该滑轮组的机械效率为多大
4. 图3-4-8中轻质横杆AB可绕固定点O在竖直平面内转动, 系在横杆 A 端的细绳通过滑轮悬挂着重为400N的物体M.重 700N的运动员站在水平地面上用力举起横杆B端,恰好使AB在水平位置平衡,已知运动员双脚与地的接触面积为 求:
(1)运动员对横杆 B端施力的大小;
(2)运动员对地的压强.
5. 造福于资阳人民的“毗河引水”工程正在如火如荼地进行建设,如图3-4-9所示为乐至县境内某引水渡槽建设工地用升降机从地面提升渡槽组件的示意图.若渡槽设计高度为 .每一段组件质量为 升降机最大功率为 每根钢丝绳上能承受的最大拉力是 不计滑轮和钢丝绳的重力及摩擦力,取 求:
(1)该升降机一次最多能匀速提升多少段渡槽组件;
(2)某次提升中,升降机最大功率在 内将3段渡槽组件从地面匀速提升值设计高度,求钢丝绳拉力的功率 P 和升降机的机械效率η.
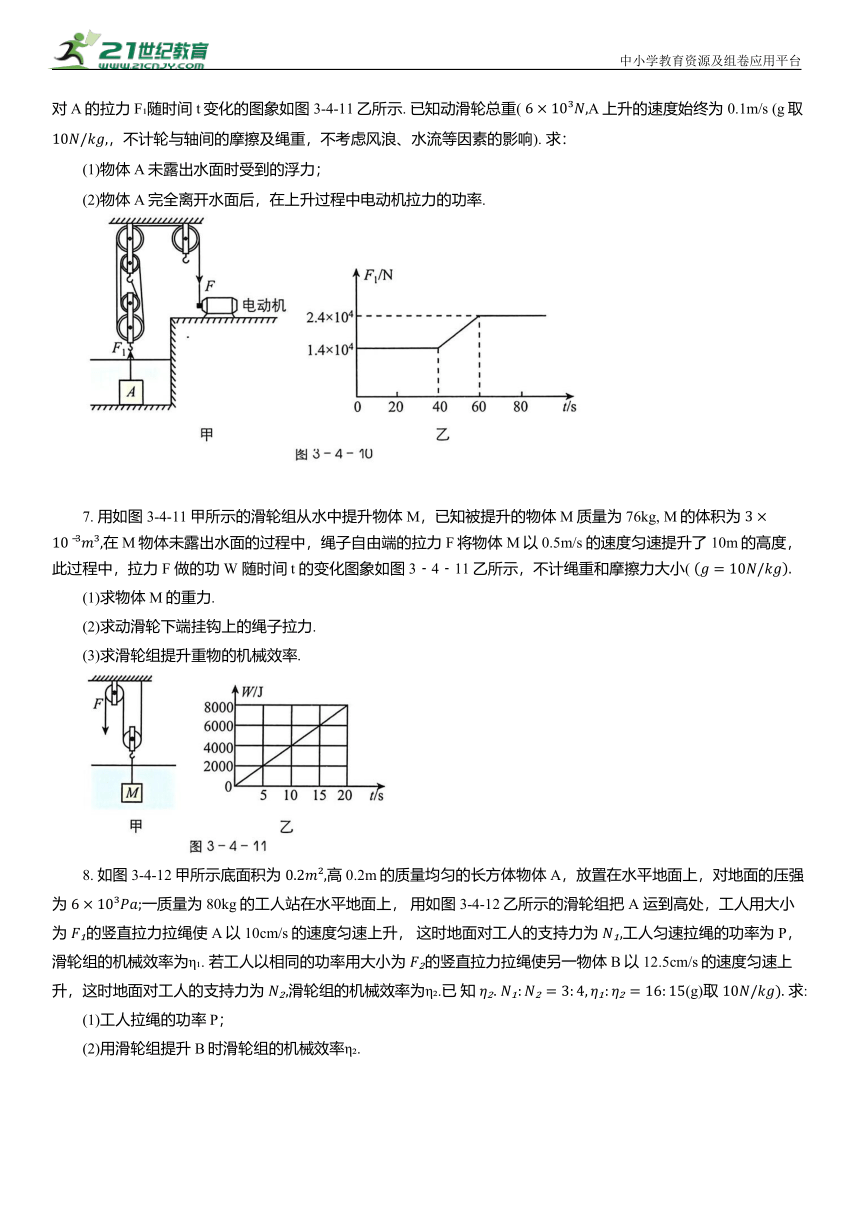
6. 图3﹣4﹣10甲是一个起吊装置示意图,使用电动机和滑轮组将物体A 从江底沿竖直方向匀速吊起,钢缆绳对A的拉力F 随时间t变化的图象如图3-4-11乙所示. 已知动滑轮总重( A上升的速度始终为0.1m/s (g取 ,不计轮与轴间的摩擦及绳重,不考虑风浪、水流等因素的影响). 求:
(1)物体A未露出水面时受到的浮力;
(2)物体A完全离开水面后,在上升过程中电动机拉力的功率.
7. 用如图3-4-11甲所示的滑轮组从水中提升物体M,已知被提升的物体M质量为76kg, M的体积为 在M物体未露出水面的过程中,绳子自由端的拉力F将物体M以0.5m/s的速度匀速提升了 10m的高度,此过程中,拉力 F 做的功 W 随时间t 的变化图象如图3﹣4﹣11乙所示,不计绳重和摩擦力大小(
(1)求物体M的重力.
(2)求动滑轮下端挂钩上的绳子拉力.
(3)求滑轮组提升重物的机械效率.
8. 如图3-4-12甲所示底面积为 高0.2m的质量均匀的长方体物体A,放置在水平地面上,对地面的压强为 一质量为80kg的工人站在水平地面上, 用如图3-4-12乙所示的滑轮组把 A 运到高处,工人用大小为 的竖直拉力拉绳使A以 10cm/s的速度匀速上升, 这时地面对工人的支持力为 工人匀速拉绳的功率为 P,滑轮组的机械效率为η . 若工人以相同的功率用大小为 的竖直拉力拉绳使另一物体B以 12.5cm/s的速度匀速上升,这时地面对工人的支持力为 滑轮组的机械效率为η .已 知 (g)取 求:
(1)工人拉绳的功率P;
(2)用滑轮组提升B时滑轮组的机械效率η .
9.用如图3-4-13甲所示的滑轮组提升水中的物体 动滑轮 A 所受重力为 物体 完全在水面下以速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为 拉力F 做功的功率为 滑轮组的机械效率为 为 了提高滑轮组的机械效率,用所受重力为 的动滑轮B替换动滑轮A,如图3-4-13乙所示,用替换动滑轮后的滑轮组提升水中的物体 物体 完全在水面下以相同的速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为 拉力 做功的功率为 滑轮组的机械效率为η .已知: 两物体的质量相等,体积Ⅴ均为 g 取 绳重、轮与轴的摩擦及水的阻力均可忽略不计. 求:
(1) 物体 受到的浮力
(2) 拉力 与 之比;
(3) 物体 M 受到的重力G.
10. 如图3-4-14所示,AB是一杠杆,可绕支点O在竖直平面内转动, 滑 轮重为10N.当在B点施加大小为F 的竖直向下的拉力时,杠杆在水平位置平衡,边长为0.1m的正方体M对水平地面的压强为 10000Pa;当在D点施加大小为F 的竖直向下的拉力时,杠杆在水平位置平衡,正方体 M对水平地面的压强为 20000Pa,不计杠杆重、绳重和摩擦, 图中各段绳子所受拉力均沿竖直方向. 求:
(1)正方体M的受到的重力;
(2)拉力 F的大小.
11. 如图3-4-15所示装置中,轻质杠杆支点为O,物块A、B通过轻质细线悬于Q点,当柱形薄壁容器中没有液体时,物体C悬挂于E 点. 杠杆在水平位置平衡; 当往容器中加入质量为 的水时,为使杠杆在水平位置平衡,物块C应悬于F 点. A、B 为均匀实心正方体,A、B的边长均为a. 连接A、B的细线长为b,B的下表面到容器底的距离也为b,柱形容器底面积为 S. 已知: O、Q两点间的距离为 三个物块的重为G kg.杠杆重力对平衡的影响忽略不计,细线重力忽略不计,物块不吸水. 求:
(1) O、E两点间的距离,
(2) E、F两点间的距离LEF.
(3)如果剪断物块A上方的细线,往容器中加水,直到容器中水的质量为 则物块处于平衡位置后,水对物块B上表面的压力
第四节 机械及其效率
学思路
铺垫 1
答案 解:(1)有用功: = 8000J;
(2) 由 得拉力 F 做的功: ×50s= 10000J,
使用动滑轮的机械效率:
答:(1) 有用功为8000J;
(2)动滑轮匀速提升建筑材料 A 的机械效率为 80%.
铺垫2
答案 解:(1)由图可知,滑轮组中由3段绳子承担重物,
则物体上升的速度为: 0.4m/s,
物体由井底拉至井口需要的时间:
(2)滑轮组的机械效率为:
=66.7%;
(3)由题意可得,汽车受到的阻力为:
汽车匀速直线运动,受到平衡力作用,在水平方向上,汽车受到向右的牵引力、 向左的拉力、 向左的阻力作用;
由力的平衡条件可得牵引力: 10 N+ 1500N=3500N;
(4)汽车运动的距离: =30m;
牵引力做功为: ×10 J.
答:(1)若汽车运动的速度为1.2m/s,则将物体由井底拉至井口,需要25s;
(2) 滑轮组的机械效率是66.7%;
(3) 汽车的牵引力是3500N;
(4)将物体由井底拉至井口,汽车的牵引力做的功是1.05×10 J.
压轴题
答案 解:(1)A完全浸没在水中时受到的浮力:F ×
(2)物体 A 的重力:G= mg =280kg×9.8N/kg=2744N,
A完全浸没在水中时,总功为 F浮)h,有用功为 所以,滑轮组的机械效率:
解得:
由图可知, n=5,
A 完全打捞出水面后,岸上钢绳的拉力:F = ;
(3) A完全打捞出水面后,以0.1m/s的速度被匀速提升时,绳端的速度:
岸上钢绳拉力F的功率:
答: (1)A 完全 浸没 在 水 中 时 受 到的 浮力是 980N;
(2)A完全打捞出水面后,岸上钢绳的拉力 F为 784N;
(3) 岸上钢绳拉力 F的功率为392W.
提能力
1. 答案 A
解析 (1)G 在 C 点时,由杠杆平衡条件得: 即: ×10cm,
解得:
物体与地面的接触面积:S = 5cm × 5cm =
由 得:物体G 对地面的压力:F= pS=
地面对物体的支持力:
G 受竖直向下的重力 G 、地面的支持力 F'、绳子的拉力 FA作用,
物体静止, 处于平衡状态, 由平衡条件得:
(2)当 G 对地面的压力为O时,杠杆在 A 点的受到的拉力
设G 位于 D 点,由杠杆平衡条件得:FA'× 即: 60N×20cm=20N×OD,解得: OD=60cm,
物体 G 的路程: s = OD- OC = 60cm- 10cm=50cm,
由 得:物体 G 的运动时间:
故选 A.
2.答案 B.
解析 (1)由图乙可知,在0~1s内,拉力F=30N.取动滑轮和重物为研究对象,受到向下的重力 G 和G动,向上的支持力 F支,及三根绳子向上的拉力 F'作用,处于静止状态;地面对重物的支持力 故 A错误;
(2)由图可知在2~3s内,重物做匀速运动, 拉力
因为从动滑轮上直接引出的绳子股数 (承担物重的绳子股数)n=3,
所以拉力F的作用点下降的速度 ×2.50m/s=7.5m/s,
拉力做功功率 (总功率): 7.5m/s=300W, 故C错误;
滑轮组的机械效率: 故 D错误;
(3) 在1~2s内, 拉力 重物上升高度
拉力 F的作用点下降的距离
拉力做的功:
故 B
正确.
3. 答案 (1) 80000; (2) 10; (3) 该滑轮组的机械效率为98%.
解析 (1)由图乙知,汽车匀速前进 20m时,拉力 F总共做的功:
(2)由图甲知,n=2,因为绳端移动的距离s=2h,
所以物体M上升的高度:
(3) 有 用 功: = 78400J;
滑轮 组的 机 械效率:
4. 答案 解:分别对物体M、杠杆AB和人进行受力分析,如下图所示:
(1)由杠杆平衡: 得:
答: (1)运动员对横杆 B端施力的大小为320N; (2) 运动员对地的压强为2.04×10 Pa.
5. 答案 解:(1)每一段组件的重力G=mg=2 滑轮组的最大拉力F =3×4×10 N=1.2×10 N,
渡槽组件的段数: 段;
(2)钢丝绳拉力做的有用功:
钢丝绳拉力的功率 3×10 w,
总功 升降机的机械效率 ×100%=75%.
答:(1)升降机一次最多能匀速提升6段渡槽组件;
(2) 钢丝绳拉力的功率3×10 W; 升降机的机械效率 75%.
6. 答案 解:物体浸在水中被匀速提起时F=G-F浮,物体露出水面时,F浮减小,F增大,当物体完全露出水面时,F=G,
(1)由图象可知,长方体A的重力 10 N,
它完全在水中时钢缆绳对其拉力为 10 N,
所以,长方体A未露出水面时受到的浮力:
10 N;
(2)滑轮组有4段绳子承担总重,
物体完全离开水平时, 电动机的拉力:F = =0.75×10 N,
则 F移动的速度:v=4×0.1m/s=0.4m/s;故拉力 F的功率:
答:(1)物体A未露出水面时受到的浮力为1×10 N;
(2)物体 A 完全离开水面后,在上升过程中电动机拉力的功率为3000W.
7. 答案 解: (1) 物体 M的重力: G=mg=76kg×10N/kg=760N;
(2)物体M浸没在水中,则
物体 M 受到的浮力:
则动滑轮下端挂钩上的绳子拉力: F浮 =760N-30N=730N;
(3)由于物体未露出水面,物体受浮力作用,则滑轮组提升重物所做的有用功:
货物以0. 5m/s 的速度匀速提 升 到 10m 的高度,
运动的时间: 由图乙可知,此时拉力做的总功是8000J,
所以滑轮组提升重物的机械效率:
答: (1) 物体M的重力为 760N;
(2)动滑轮下端挂钩上的绳子拉力为730N;
(3)滑轮组提升重物的机械效率为91.25%.
8. 答案 解:(1)对工人, 由平衡条件得:F+N=m,g=80kg×10N/kg=800N,
则:
由题意可知: 则: 44F -3F
=800N ①
提升物体时的功率相等, 解得: ②
由①②解得: 工人拉绳子的功率:
P=F v =500N×0.1m/s×3= 150W;
(2)滑轮组效率: 由题意可知:
答: (1) 工人拉绳的功率 P 为 150W;
(2)用滑轮组提升 B时滑轮组的机械效率η 为 75%.
9. 答案 解:(1)物体 M 受到的浮力: ×10 N;
(3)以动滑轮和物体 M为研究对象,受力分析如题甲、乙所示,
G=760N.
答: (1) 4×10 N; (2) 16: 15; (3) 760N.
10.答案 解: 正方体底面积S=0.1m×0.1m=0.01m ;
(1)当 F作用B 点时,杠杆、动滑轮、正方体 M受力如图甲所示;
由杠杆平 衡条件可得:F × AO = F×OB,AO:OB=1:2, 得.
由平衡条件得, 则f =2F
因为 所以N = p S= 10000Pa×0.01
即 100N=G- (4F-10N), 则90N=G-4F①
(2)当 F 作用D 点时,杠杆、动滑轮、正方体 M受力如图乙所示,
由杠杆平衡条件得:F ×AO=F×OD,
AO: OB = 1 : 2, OD : OB = 1 : 1, 得 F = F,
对滑轮, - 10N, 因 为 所 以
对 M: 则 190N= G-2F ②,由①②两式解得: G=290N, F=50N.
答: (1) 正方体M的受到的重力为290N;
(2) 拉力 F 的大小为50N.
11.答案 解:(1)当柱形薄壁容器中没有液体时,物体C悬挂于E 点.杠杆在水平位置平衡;由图知,O 为支点,Q 为阻力作用点,F =GA + GB=0.016N+0.128N=0. 144N,QO 为阻力臂,动力 OE 为动力臂;
根据杠杆的平衡条件可得: LoE, 所 以, =14.4cm;
(2)当往容器中加入质量为m 的水时,加入的水的体积为: cm ,由于 B物体下面的空余体积为
A、B 物体的底面积
则 B物体进入水的深度为
则 B物体受到的浮力 0.01m=0.04N;
所以此时对杠杆的拉力为 FB浮 =0.016N+0.128N-0.04N=0.104N,根据杠杆的平衡条件可得: ×LoF,
所 以 10.4cm, 则 10.4cm=4cm;
(3)剪断物块A 上方的细线,往容器中加水,直到容器中水的质量为 时,假设AB物体都浸没,则 0.08N,
则
所以A、B物体是整体,处于漂浮状态,由于 所以最后的状态是 A 部分体积漏出水面,且 A、B处于漂浮;
则 0.144N,
由 可 得: 所以,
则 物 体 A 浸 入 水 的 深 度 由图可知此时物块 B上表面所处的深度 1.6cm+2cm=3.6cm=0.036m,
p'=ρxgh'=1×10 kg/m ×10N/kg×0.036m=360Pa,
答: (1) O、E两点间的距离LoE =14.4cm;
(2) E、F两点间的距离LEF =4cm;
(3)物块处于平衡位置后,水对物块 B 上表面的压力
机械及其效率
讲方法
一、机械类题目的解题思想
1. 杠杆类题目的解题主要分为两步:
第一步:明确杠杆模型并找到杠杆五要素;
第二步:受力分析并根据杠杆平衡原理列出方程,并带入物理量解题.
2. 滑轮类题目的解题主要分为两步:
第一步: 明确滑轮的类型,并确定绳子股数n;
第二步:选定合适的研究对象,对其进行受力分析,并根据滑轮的特点列出方程,然后带入物理量解题.
二、效率类题目的解题思路
1.机械效率一般包括常规 (杠杆、滑轮、斜面等)的机械的机械效率和生活应用类 (起重机、卷扬机等)的机械效率.不管哪种机械的机械效率,我们都需要找到三个关键的物理量:有用功、额外功和总功,在不同的情景中,这三个物理量所对应的表达式不同,我们需要认真分析.
2. 常规情景下的机械效率计算:
(1) 垂直使用滑轮组时 (如图3-4-1甲, 不计绳重及摩擦):
(2)垂直使用滑轮组日物体在液体中时 (如图3-4-1乙, 不计绳重及摩擦):
(3)水平使用滑轮组时 (如图3-4-1丙):
(4)斜面的机械效率 (如图3-4-1丁所示):
学思路
铺垫1
如 图 3 -4 --2 是 用动滑轮运送建筑材料A的示意图,在卷扬机对绳子的拉力作用下,使重 800N的建筑材料 A 在50s的时间里,匀速竖直上升了 10m.在这个过程中,动滑轮提升建筑材料A所 做 的 有 用 功 为 W有, 卷扬机对绳子的拉力 F做功的功率为200W.绳重可忽略不计. 求:
(1) 有用功W有;
(2)动滑轮匀速提升建筑材料A的机械效率η.
铺垫2
如图 3 -4-3 所示,是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图,已知井深 10m,物体重G=4×10 N, 汽车重 ,汽车匀速拉绳子时的拉力. N,汽车受到的阻力为车重的0.05倍. 请计算:
(1)若汽车 运 动 的 速 度 为 1.2m/s, 则 将物 体 由 井 底 拉 至 井 口,需要多长时间
(2)滑轮组的机械效率是多少 (保留一位小数)
(3)汽车的牵引力是多大
(4)将物体由井底拉至井口,汽车的牵引力做的功是多少
压轴题
考古学家在黄海海域发现甲午海战沉船“致远舰”的消息轰动了整个考古界,随着水下考古工作的进行,一些重要文物陆续出水重见天日,关于这艘在海水中沉睡了 120余年的战舰是如何被打捞起的谜题也逐步解开.现某课外活动小组,照此设计了如图3-4-4所示的简单机械,模拟打捞沉船,实验中用实心立方体A代替沉船,已知A的体积为0.1m ,质量为280kg (设整个过程A均为匀速直线运动状态,忽略钢缆绳重及滑轮摩擦,不考虑风浪,水流等因素的影响,
(1)A完全浸没在水中时受到的浮力是多大
(2)若A完全浸没在水中时,滑轮组的机械效率为60%,那么A完全打捞出水面后,岸上钢绳的拉力 F 为多大
(3)若A完全打捞出水面后,以0.1m/s的速度被匀速提升,求岸上钢绳拉力F的功率.
提能力
1. 如图3-4-5所示,一轻质杠杆AB支在支架上, 为一边长为5cm的正方体, 重为20N.当 时, 对地面的压强为 .现用一水平拉力 F使 以 的速度向右匀速运动,则当 对地面的压力为0时所经过的时间为 ( )
A. 25s
B. 30s
C. 35s
D. 40s
2. 为了将放置在水平地面上重为100N的物体提升一定高度,设置了图3-4-6甲所示的滑轮组装置. 当用图3-4-6乙所示随时间变化的竖直向下的拉力F拉绳时,物体的速度v和物体上升的高度h随时间变化的关系分别如图3-4-6丙和图3-4-6丁所示. (不计绳重和绳与轮之间的摩擦)下列计算结果正确的是 ( )
A. Os~1s内, 地面对物体的支持力是 10N
B. 1s~2s内, 拉力 F做的功是 187.5J
C. 2s~3s内, 拉力 F 的功率是 100W
D. 2s~3s内, 滑轮组的机械效率是62.5%
3.如图3-4-7甲所示,用滑轮组提升矿井内重为7840N的物体M,汽车匀速前进了20m.此过程中,汽车拉力F所做的功W随汽车运动的距离s的变化关系如图3-4-7乙所示. 不计绳重和摩擦,动滑轮有重力.
(1) 由图可知,拉力 F总共做的功W= J.
(2)物体M上升的高度是 m.
(3)该滑轮组的机械效率为多大
4. 图3-4-8中轻质横杆AB可绕固定点O在竖直平面内转动, 系在横杆 A 端的细绳通过滑轮悬挂着重为400N的物体M.重 700N的运动员站在水平地面上用力举起横杆B端,恰好使AB在水平位置平衡,已知运动员双脚与地的接触面积为 求:
(1)运动员对横杆 B端施力的大小;
(2)运动员对地的压强.
5. 造福于资阳人民的“毗河引水”工程正在如火如荼地进行建设,如图3-4-9所示为乐至县境内某引水渡槽建设工地用升降机从地面提升渡槽组件的示意图.若渡槽设计高度为 .每一段组件质量为 升降机最大功率为 每根钢丝绳上能承受的最大拉力是 不计滑轮和钢丝绳的重力及摩擦力,取 求:
(1)该升降机一次最多能匀速提升多少段渡槽组件;
(2)某次提升中,升降机最大功率在 内将3段渡槽组件从地面匀速提升值设计高度,求钢丝绳拉力的功率 P 和升降机的机械效率η.
6. 图3﹣4﹣10甲是一个起吊装置示意图,使用电动机和滑轮组将物体A 从江底沿竖直方向匀速吊起,钢缆绳对A的拉力F 随时间t变化的图象如图3-4-11乙所示. 已知动滑轮总重( A上升的速度始终为0.1m/s (g取 ,不计轮与轴间的摩擦及绳重,不考虑风浪、水流等因素的影响). 求:
(1)物体A未露出水面时受到的浮力;
(2)物体A完全离开水面后,在上升过程中电动机拉力的功率.
7. 用如图3-4-11甲所示的滑轮组从水中提升物体M,已知被提升的物体M质量为76kg, M的体积为 在M物体未露出水面的过程中,绳子自由端的拉力F将物体M以0.5m/s的速度匀速提升了 10m的高度,此过程中,拉力 F 做的功 W 随时间t 的变化图象如图3﹣4﹣11乙所示,不计绳重和摩擦力大小(
(1)求物体M的重力.
(2)求动滑轮下端挂钩上的绳子拉力.
(3)求滑轮组提升重物的机械效率.
8. 如图3-4-12甲所示底面积为 高0.2m的质量均匀的长方体物体A,放置在水平地面上,对地面的压强为 一质量为80kg的工人站在水平地面上, 用如图3-4-12乙所示的滑轮组把 A 运到高处,工人用大小为 的竖直拉力拉绳使A以 10cm/s的速度匀速上升, 这时地面对工人的支持力为 工人匀速拉绳的功率为 P,滑轮组的机械效率为η . 若工人以相同的功率用大小为 的竖直拉力拉绳使另一物体B以 12.5cm/s的速度匀速上升,这时地面对工人的支持力为 滑轮组的机械效率为η .已 知 (g)取 求:
(1)工人拉绳的功率P;
(2)用滑轮组提升B时滑轮组的机械效率η .
9.用如图3-4-13甲所示的滑轮组提升水中的物体 动滑轮 A 所受重力为 物体 完全在水面下以速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为 拉力F 做功的功率为 滑轮组的机械效率为 为 了提高滑轮组的机械效率,用所受重力为 的动滑轮B替换动滑轮A,如图3-4-13乙所示,用替换动滑轮后的滑轮组提升水中的物体 物体 完全在水面下以相同的速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为 拉力 做功的功率为 滑轮组的机械效率为η .已知: 两物体的质量相等,体积Ⅴ均为 g 取 绳重、轮与轴的摩擦及水的阻力均可忽略不计. 求:
(1) 物体 受到的浮力
(2) 拉力 与 之比;
(3) 物体 M 受到的重力G.
10. 如图3-4-14所示,AB是一杠杆,可绕支点O在竖直平面内转动, 滑 轮重为10N.当在B点施加大小为F 的竖直向下的拉力时,杠杆在水平位置平衡,边长为0.1m的正方体M对水平地面的压强为 10000Pa;当在D点施加大小为F 的竖直向下的拉力时,杠杆在水平位置平衡,正方体 M对水平地面的压强为 20000Pa,不计杠杆重、绳重和摩擦, 图中各段绳子所受拉力均沿竖直方向. 求:
(1)正方体M的受到的重力;
(2)拉力 F的大小.
11. 如图3-4-15所示装置中,轻质杠杆支点为O,物块A、B通过轻质细线悬于Q点,当柱形薄壁容器中没有液体时,物体C悬挂于E 点. 杠杆在水平位置平衡; 当往容器中加入质量为 的水时,为使杠杆在水平位置平衡,物块C应悬于F 点. A、B 为均匀实心正方体,A、B的边长均为a. 连接A、B的细线长为b,B的下表面到容器底的距离也为b,柱形容器底面积为 S. 已知: O、Q两点间的距离为 三个物块的重为G kg.杠杆重力对平衡的影响忽略不计,细线重力忽略不计,物块不吸水. 求:
(1) O、E两点间的距离,
(2) E、F两点间的距离LEF.
(3)如果剪断物块A上方的细线,往容器中加水,直到容器中水的质量为 则物块处于平衡位置后,水对物块B上表面的压力
第四节 机械及其效率
学思路
铺垫 1
答案 解:(1)有用功: = 8000J;
(2) 由 得拉力 F 做的功: ×50s= 10000J,
使用动滑轮的机械效率:
答:(1) 有用功为8000J;
(2)动滑轮匀速提升建筑材料 A 的机械效率为 80%.
铺垫2
答案 解:(1)由图可知,滑轮组中由3段绳子承担重物,
则物体上升的速度为: 0.4m/s,
物体由井底拉至井口需要的时间:
(2)滑轮组的机械效率为:
=66.7%;
(3)由题意可得,汽车受到的阻力为:
汽车匀速直线运动,受到平衡力作用,在水平方向上,汽车受到向右的牵引力、 向左的拉力、 向左的阻力作用;
由力的平衡条件可得牵引力: 10 N+ 1500N=3500N;
(4)汽车运动的距离: =30m;
牵引力做功为: ×10 J.
答:(1)若汽车运动的速度为1.2m/s,则将物体由井底拉至井口,需要25s;
(2) 滑轮组的机械效率是66.7%;
(3) 汽车的牵引力是3500N;
(4)将物体由井底拉至井口,汽车的牵引力做的功是1.05×10 J.
压轴题
答案 解:(1)A完全浸没在水中时受到的浮力:F ×
(2)物体 A 的重力:G= mg =280kg×9.8N/kg=2744N,
A完全浸没在水中时,总功为 F浮)h,有用功为 所以,滑轮组的机械效率:
解得:
由图可知, n=5,
A 完全打捞出水面后,岸上钢绳的拉力:F = ;
(3) A完全打捞出水面后,以0.1m/s的速度被匀速提升时,绳端的速度:
岸上钢绳拉力F的功率:
答: (1)A 完全 浸没 在 水 中 时 受 到的 浮力是 980N;
(2)A完全打捞出水面后,岸上钢绳的拉力 F为 784N;
(3) 岸上钢绳拉力 F的功率为392W.
提能力
1. 答案 A
解析 (1)G 在 C 点时,由杠杆平衡条件得: 即: ×10cm,
解得:
物体与地面的接触面积:S = 5cm × 5cm =
由 得:物体G 对地面的压力:F= pS=
地面对物体的支持力:
G 受竖直向下的重力 G 、地面的支持力 F'、绳子的拉力 FA作用,
物体静止, 处于平衡状态, 由平衡条件得:
(2)当 G 对地面的压力为O时,杠杆在 A 点的受到的拉力
设G 位于 D 点,由杠杆平衡条件得:FA'× 即: 60N×20cm=20N×OD,解得: OD=60cm,
物体 G 的路程: s = OD- OC = 60cm- 10cm=50cm,
由 得:物体 G 的运动时间:
故选 A.
2.答案 B.
解析 (1)由图乙可知,在0~1s内,拉力F=30N.取动滑轮和重物为研究对象,受到向下的重力 G 和G动,向上的支持力 F支,及三根绳子向上的拉力 F'作用,处于静止状态;地面对重物的支持力 故 A错误;
(2)由图可知在2~3s内,重物做匀速运动, 拉力
因为从动滑轮上直接引出的绳子股数 (承担物重的绳子股数)n=3,
所以拉力F的作用点下降的速度 ×2.50m/s=7.5m/s,
拉力做功功率 (总功率): 7.5m/s=300W, 故C错误;
滑轮组的机械效率: 故 D错误;
(3) 在1~2s内, 拉力 重物上升高度
拉力 F的作用点下降的距离
拉力做的功:
故 B
正确.
3. 答案 (1) 80000; (2) 10; (3) 该滑轮组的机械效率为98%.
解析 (1)由图乙知,汽车匀速前进 20m时,拉力 F总共做的功:
(2)由图甲知,n=2,因为绳端移动的距离s=2h,
所以物体M上升的高度:
(3) 有 用 功: = 78400J;
滑轮 组的 机 械效率:
4. 答案 解:分别对物体M、杠杆AB和人进行受力分析,如下图所示:
(1)由杠杆平衡: 得:
答: (1)运动员对横杆 B端施力的大小为320N; (2) 运动员对地的压强为2.04×10 Pa.
5. 答案 解:(1)每一段组件的重力G=mg=2 滑轮组的最大拉力F =3×4×10 N=1.2×10 N,
渡槽组件的段数: 段;
(2)钢丝绳拉力做的有用功:
钢丝绳拉力的功率 3×10 w,
总功 升降机的机械效率 ×100%=75%.
答:(1)升降机一次最多能匀速提升6段渡槽组件;
(2) 钢丝绳拉力的功率3×10 W; 升降机的机械效率 75%.
6. 答案 解:物体浸在水中被匀速提起时F=G-F浮,物体露出水面时,F浮减小,F增大,当物体完全露出水面时,F=G,
(1)由图象可知,长方体A的重力 10 N,
它完全在水中时钢缆绳对其拉力为 10 N,
所以,长方体A未露出水面时受到的浮力:
10 N;
(2)滑轮组有4段绳子承担总重,
物体完全离开水平时, 电动机的拉力:F = =0.75×10 N,
则 F移动的速度:v=4×0.1m/s=0.4m/s;故拉力 F的功率:
答:(1)物体A未露出水面时受到的浮力为1×10 N;
(2)物体 A 完全离开水面后,在上升过程中电动机拉力的功率为3000W.
7. 答案 解: (1) 物体 M的重力: G=mg=76kg×10N/kg=760N;
(2)物体M浸没在水中,则
物体 M 受到的浮力:
则动滑轮下端挂钩上的绳子拉力: F浮 =760N-30N=730N;
(3)由于物体未露出水面,物体受浮力作用,则滑轮组提升重物所做的有用功:
货物以0. 5m/s 的速度匀速提 升 到 10m 的高度,
运动的时间: 由图乙可知,此时拉力做的总功是8000J,
所以滑轮组提升重物的机械效率:
答: (1) 物体M的重力为 760N;
(2)动滑轮下端挂钩上的绳子拉力为730N;
(3)滑轮组提升重物的机械效率为91.25%.
8. 答案 解:(1)对工人, 由平衡条件得:F+N=m,g=80kg×10N/kg=800N,
则:
由题意可知: 则: 44F -3F
=800N ①
提升物体时的功率相等, 解得: ②
由①②解得: 工人拉绳子的功率:
P=F v =500N×0.1m/s×3= 150W;
(2)滑轮组效率: 由题意可知:
答: (1) 工人拉绳的功率 P 为 150W;
(2)用滑轮组提升 B时滑轮组的机械效率η 为 75%.
9. 答案 解:(1)物体 M 受到的浮力: ×10 N;
(3)以动滑轮和物体 M为研究对象,受力分析如题甲、乙所示,
G=760N.
答: (1) 4×10 N; (2) 16: 15; (3) 760N.
10.答案 解: 正方体底面积S=0.1m×0.1m=0.01m ;
(1)当 F作用B 点时,杠杆、动滑轮、正方体 M受力如图甲所示;
由杠杆平 衡条件可得:F × AO = F×OB,AO:OB=1:2, 得.
由平衡条件得, 则f =2F
因为 所以N = p S= 10000Pa×0.01
即 100N=G- (4F-10N), 则90N=G-4F①
(2)当 F 作用D 点时,杠杆、动滑轮、正方体 M受力如图乙所示,
由杠杆平衡条件得:F ×AO=F×OD,
AO: OB = 1 : 2, OD : OB = 1 : 1, 得 F = F,
对滑轮, - 10N, 因 为 所 以
对 M: 则 190N= G-2F ②,由①②两式解得: G=290N, F=50N.
答: (1) 正方体M的受到的重力为290N;
(2) 拉力 F 的大小为50N.
11.答案 解:(1)当柱形薄壁容器中没有液体时,物体C悬挂于E 点.杠杆在水平位置平衡;由图知,O 为支点,Q 为阻力作用点,F =GA + GB=0.016N+0.128N=0. 144N,QO 为阻力臂,动力 OE 为动力臂;
根据杠杆的平衡条件可得: LoE, 所 以, =14.4cm;
(2)当往容器中加入质量为m 的水时,加入的水的体积为: cm ,由于 B物体下面的空余体积为
A、B 物体的底面积
则 B物体进入水的深度为
则 B物体受到的浮力 0.01m=0.04N;
所以此时对杠杆的拉力为 FB浮 =0.016N+0.128N-0.04N=0.104N,根据杠杆的平衡条件可得: ×LoF,
所 以 10.4cm, 则 10.4cm=4cm;
(3)剪断物块A 上方的细线,往容器中加水,直到容器中水的质量为 时,假设AB物体都浸没,则 0.08N,
则
所以A、B物体是整体,处于漂浮状态,由于 所以最后的状态是 A 部分体积漏出水面,且 A、B处于漂浮;
则 0.144N,
由 可 得: 所以,
则 物 体 A 浸 入 水 的 深 度 由图可知此时物块 B上表面所处的深度 1.6cm+2cm=3.6cm=0.036m,
p'=ρxgh'=1×10 kg/m ×10N/kg×0.036m=360Pa,
答: (1) O、E两点间的距离LoE =14.4cm;
(2) E、F两点间的距离LEF =4cm;
(3)物块处于平衡位置后,水对物块 B 上表面的压力
同课章节目录
