2024—2025学年上学期福建初中数学七年级开学模拟试卷2(含解析+考点卡片)
文档属性
| 名称 | 2024—2025学年上学期福建初中数学七年级开学模拟试卷2(含解析+考点卡片) |  | |
| 格式 | docx | ||
| 文件大小 | 280.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 08:33:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024—2025学年上学期福建初中数学七年级开学模拟试卷2
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)在5:7中,如果比的后项加上7,要使比值不变,前项应( )
A.加上7 B.乘7 C.乘2 D.加2
2.(2分)比﹣2小的数是( )
A.﹣3 B.﹣1 C.0 D.1
3.(2分)一根红色电线和一根蓝色电线一样长,红的剪去,蓝的剪去米,红的剩下的比蓝的短,原来这两根电线( )1米.
A.大于 B.小于 C.等于 D.都有可能
4.(2分)把一个长为2毫米的零件画在图纸上,在图纸上量得这个零件的长是2分米,则这幅图的比例尺是( )
A.1:100 B.1:1 C.100:1 D.100
5.(2分)张老师在化学实验室做实验时,将一杯100℃的开水放在石棉网上自然冷却至室温.水温T(℃)与时间t(min)的对应关系如图所示.根据图中所显示的信息,下列说法错误的是( )
A.水温从100℃逐渐下降到35℃时用了6min
B.当t=20时,水温是10℃
C.水温随时间的增加而降低
D.当0<t<10时,水温下降速度逐渐变慢
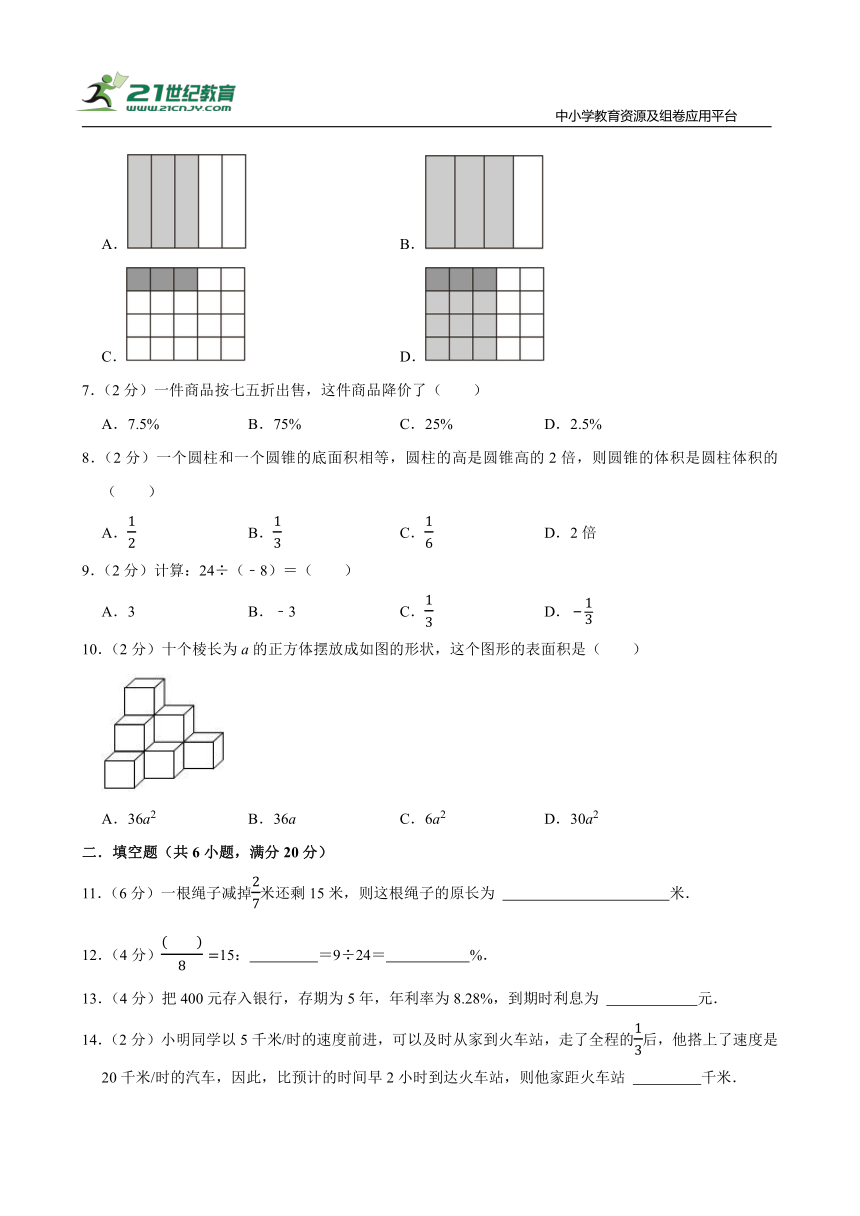
6.(2分)图中,可以表示计算过程的是( )
A. B.
C. D.
7.(2分)一件商品按七五折出售,这件商品降价了( )
A.7.5% B.75% C.25% D.2.5%
8.(2分)一个圆柱和一个圆锥的底面积相等,圆柱的高是圆锥高的2倍,则圆锥的体积是圆柱体积的( )
A. B. C. D.2倍
9.(2分)计算:24÷(﹣8)=( )
A.3 B.﹣3 C. D.
10.(2分)十个棱长为a的正方体摆放成如图的形状,这个图形的表面积是( )
A.36a2 B.36a C.6a2 D.30a2
二.填空题(共6小题,满分20分)
11.(6分)一根绳子减掉米还剩15米,则这根绳子的原长为 米.
12.(4分)15: =9÷24= %.
13.(4分)把400元存入银行,存期为5年,年利率为8.28%,到期时利息为 元.
14.(2分)小明同学以5千米/时的速度前进,可以及时从家到火车站,走了全程的后,他搭上了速度是20千米/时的汽车,因此,比预计的时间早2小时到达火车站,则他家距火车站 千米.
15.(2分)如图,长方形ABCD中,AB=5厘米,BC=3厘米,把长方形ABCD绕顶点B顺时针转动,使点A落在点A′处,点C落在点C′处,且点A、B、C′三点在一条直线上,则A点和C点所经过的路程之比为 .
16.(2分)我国木雕艺术历史悠久.如图1为一木雕的实物图,如图2此木雕可以近似地看作扇环,其中OC长为0.2米,AC长为0.5米,∠COD为100°,则木雕的面积(镂空部分忽略不计)为 平方米.(结果保留π)
三.解答题(共1小题,满分30分,每小题30分)
17.(30分)计算:
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)解方程:.
四.解答题(共7小题,满分50分)
18.(7分)如图,甲、乙、丙三个容器,甲为立方体,内壁的各条棱长为8厘米;乙为圆柱体,内壁高6厘米,内部底面半径为3厘米;丙是长方体,长12厘米,宽6厘米,高6厘米.现将甲容器盛满酒精,把甲容器内的酒精倒入与乙相同的2个容器,倒满后,把剩下的酒精倒入丙容器,求丙容器内酒精的高度(π取3,结果精确到0.1厘米).
19.(7分)已知x、y为有理数,现规定一种新运算※,满足x※y=3y﹣2x.
(1)求2※3的值;
(2)化简a※(2a+3).
20.(7分)实验小学购进鲜花150盆,其中摆放在大门两旁,其余的按2:3分别摆在教学楼和实验楼前,教学楼和实验楼前各放了多少盆鲜花?
21.(7分)A、B两地相距900米.甲乙二人同时从A地前往B地,甲每分钟行70米,乙每分钟行50米,甲到达B地后马上返回,与乙在途中相遇,两人从出发到相遇一共用了多少时间?
22.(7分)要在规定天数内修筑一段公路,若让甲队单独修筑,则正好在规定天数内按期完成;若让乙队单独修筑,则要比规定天数多8天才完成.现在由乙队单独修筑其中一小段,用去了规定时间的一半,然后甲队接着单独修筑2天,这段公路还有一半未修筑.若让两队共同再修筑2天,能否完成任务?
23.(7分)列一元一次方程解应用题:一列动车匀速行驶,完全通过一条长600米的隧道需要25秒的时间,隧道顶上有一盏灯,垂直向下发光,灯光照在动车上的时间是10秒,求这列动车的长度?
24.(8分)学校要修建一个圆柱形的水池,在比例尺是1:200的设计图纸上,水池的半径为3厘米,深为2厘米.
(1)按图施工,这个水池的实际应该挖多少米深?
(2)按图施工,这个水池的能装下多少立方米的水?
(3)为了加固和美观,施工时给水池底部和水池壁都铺了水泥,且平均厚度是10厘米,然后再用油漆将新铺水泥的表面粉刷一遍,请问粉刷部分的面积是多少平方米?(结果保留一位小数)
2024—2025学年上学期福建初中数学七年级开学模拟试卷2
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)在5:7中,如果比的后项加上7,要使比值不变,前项应( )
A.加上7 B.乘7 C.乘2 D.加2
【考点】比的基本性质.
【专题】实数;运算能力.
【答案】C
【分析】根据各个选项得出算式,再求出结果,最后根据求出的结果找出选项即可.
【解答】解:A.(5+7):(7+7)=12:14=6:7,和5:7不相等,故本选项不符合题意;
B.(5×7):(7+7)=35:14=5:2,和5:7不相等,故本选项不符合题意;
C.(5×2):(7+7)=10:14=5:7,故本选项符合题意;
D.(5+2):(7+7)=7:14=1:2,和5:7不相等,故本选项不符合题意.
故选:C.
【点评】本题考查了比的基本性质,能根据题意列出算式是解此题的关键.
2.(2分)比﹣2小的数是( )
A.﹣3 B.﹣1 C.0 D.1
【考点】有理数大小比较.
【专题】实数;数感.
【答案】A
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断出四个数中,比﹣2小的数是哪个数即可.
【解答】解:∵﹣3<﹣2<﹣1<0<1,
∴比﹣2小的数是﹣3.
故选:A.
【点评】此题主要考查了有理数大小比较,熟记有理数大小比较的法则是解答本题的关键.
3.(2分)一根红色电线和一根蓝色电线一样长,红的剪去,蓝的剪去米,红的剩下的比蓝的短,原来这两根电线( )1米.
A.大于 B.小于 C.等于 D.都有可能
【考点】分数的混合运算.
【专题】实数;运算能力.
【答案】A
【分析】根据分数乘法的意义解答即可.
【解答】解:假设原来这两根电线的长度为1米,则红的剪去,剩余米;蓝的剪去米,剩余米,这不符合题目中的“红的剩下的比蓝的短”的要求;
如果原来这两根电线的长度都大于1米,则红的剪去就大于米,所以红的剩下的比蓝的短,符合题意.
故选:A.
【点评】本题考查了分数的混合运算,掌握分数乘法的意义是解答本题的关键.
4.(2分)把一个长为2毫米的零件画在图纸上,在图纸上量得这个零件的长是2分米,则这幅图的比例尺是( )
A.1:100 B.1:1 C.100:1 D.100
【考点】比例尺.
【专题】尺规作图;数据分析观念.
【答案】C
【分析】根据图上距离、实际距离和比例尺的关系得出结论即可.
【解答】解:2分米=200毫米,
比例尺为200:2=100:1,
故选:C.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况.
5.(2分)张老师在化学实验室做实验时,将一杯100℃的开水放在石棉网上自然冷却至室温.水温T(℃)与时间t(min)的对应关系如图所示.根据图中所显示的信息,下列说法错误的是( )
A.水温从100℃逐渐下降到35℃时用了6min
B.当t=20时,水温是10℃
C.水温随时间的增加而降低
D.当0<t<10时,水温下降速度逐渐变慢
【考点】函数的图象.
【专题】函数及其图象;推理能力;应用意识.
【答案】C
【分析】根据图象逐项判断即可.
【解答】解:当T=100时,t=0;
当T=35时,t=6;
∴水温从100℃逐渐下降到35℃时用了6﹣0=6(min).
故A正确,不符合题意.
当t=20时,T=10,
故B正确,不符合题意.
当0≤t≤18时,T随t的增加而减小;
当t>18时,T不随t的增加而变化,恒为室温10℃.
故C不正确,符合题意.
当0<t<10时,曲线上各点的陡峭程度变得越来越小,
∴水温下降速度逐渐变慢.
故D正确,不符合题意.
故选:C.
【点评】本题考查函数的图象,这部分内容非常重要,一定要具备从图象上获取有用信息的能力.
6.(2分)图中,可以表示计算过程的是( )
A. B.
C. D.
【考点】分数的除法.
【专题】实数;数感.
【答案】D
【分析】根据图所表示的意义逐项进行分析即可.
【解答】解:由题可知,
A、阴影部分表示把单位“1”平均分成5份,再取其中的3份,用分数表示为,不符合题意;
B、阴影部分表示把单位“1”平均分成4份,再取其中的3份,用分数表示为,不符合题意;
C、阴影部分表示把单位“1”平均分成20份,再取其中的3份,用分数表示为,不符合题意;
D、阴影部分表示把单位“1”平均分成5份,再取其中的3份,用分数表示为,再把平均分成4份,取其中的1份,与算式4意义相同,符合题意.
故选:D.
【点评】本题考查分数的除法,能够根据图分析是解题的关键.
7.(2分)一件商品按七五折出售,这件商品降价了( )
A.7.5% B.75% C.25% D.2.5%
【考点】百分数的应用.
【专题】计算题;实数;运算能力;应用意识.
【答案】C
【分析】读懂题意,七五折出售,就是原价的75%,降价就是原价的1﹣75%.
【解答】解:1﹣75%=25%,
答:这件商品降价了25%.
故选:C.
【点评】本题考查了百分数的应用,解题的关键是理解打折的含义.
8.(2分)一个圆柱和一个圆锥的底面积相等,圆柱的高是圆锥高的2倍,则圆锥的体积是圆柱体积的( )
A. B. C. D.2倍
【考点】圆锥的体积;圆柱的体积.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力;推理能力.
【答案】C
【分析】由一个圆柱和一个圆锥的底面积相等,可设圆柱和圆锥的底面积为S,由圆柱的高是圆锥高的2倍,可设圆锥的高为h,圆柱的高为2h,根据圆柱与圆锥的体积公式,分别求出它们的体积,利用比的意义,即可求解.
【解答】解:设圆柱和圆锥的底面积为S,设圆锥的高为h,圆柱的高为2h,
圆柱的体积=S×2h=2Sh,圆锥的体积,
则圆锥的体积是圆柱体积的比是:,
答:圆锥的体积是圆柱体积的.
故选:C.
【点评】本题考查了圆柱与圆锥的体积计算以及比的意义的应用,灵活应用圆柱与圆锥的体积计算公式是解题的关键.
9.(2分)计算:24÷(﹣8)=( )
A.3 B.﹣3 C. D.
【考点】有理数的除法.
【专题】计算题;实数;运算能力.
【答案】B
【分析】先确定商的符号,再确定商的绝对值.
【解答】解;24÷(﹣8)=﹣3.
故选:B.
【点评】本题主要考查了有理数的运算,掌握有理数的除法法则是解决本题的关键.
10.(2分)十个棱长为a的正方体摆放成如图的形状,这个图形的表面积是( )
A.36a2 B.36a C.6a2 D.30a2
【考点】几何体的表面积;认识立体图形.
【专题】线段、角、相交线与平行线;空间观念.
【答案】A
【分析】先数出每个面的正方形的个数,然后加起来求出表面积即可.
【解答】解:由题意可得该图形的表面积为各个面的小正方形的面积之和,
∴该几何体前后左右上下各都有6个小正方形,共36个小正方形,
∵小正方体的棱长为 a,
∴该图形的表面积为36a2,
故选:A.
【点评】本题主要考查正方形的面积公式,关键是要准确数出图形外表面一共有几个正方形.
二.填空题(共6小题,满分20分)
11.(6分)一根绳子减掉米还剩15米,则这根绳子的原长为 15 米.
【考点】分数混合运算的应用.
【专题】计算题;实数;运算能力;应用意识.
【答案】15.
【分析】根据一根绳子减掉米还剩15米,则这根绳子的原长为15,然后计算即可.
【解答】解:由题意可得,
这根绳子的原长为:15=15(米),
故答案为:15.
【点评】本题考查分数混合运算的应用,解答本题的关键是明确题意,列出相应的算式.
12.(4分)15: 40 =9÷24= 37.5 %.
【考点】百分数的互化;分数的基本性质.
【专题】实数;运算能力.
【答案】3,40,37.5.
【分析】根据分数的基本性质进行解题即可.
【解答】解:9÷240.375=37.5%.
故答案为:3,40,37.5.
【点评】本题考查百分数的互化和分数的基本性质,熟练掌握相关的知识点是解题的关键.
13.(4分)把400元存入银行,存期为5年,年利率为8.28%,到期时利息为 165.6 元.
【考点】百分数的应用.
【专题】实数;运算能力;应用意识.
【答案】165.6.
【分析】根据“利息=本金×利率×存期”列出算式,即可求解.
【解答】解:根据“利息=本金×利率×存期”可得,
400×8.28%×5
=33.12×5
=165.6(元).
∴到期时利息为165.6元.
故答案为:165.6.
【点评】本题考查有理数的混合运算,解答本题是明确“利息=本金×利率×存期”.
14.(2分)小明同学以5千米/时的速度前进,可以及时从家到火车站,走了全程的后,他搭上了速度是20千米/时的汽车,因此,比预计的时间早2小时到达火车站,则他家距火车站 20 千米.
【考点】分数混合运算的应用.
【专题】应用题;一次方程(组)及应用;运算能力.
【答案】20.
【分析】根据“小明从家到火车站的时间=小明走全程的时间+小明做汽车走全程的时间+早到的时间”列出方程,并求解即可.
【解答】解:小明同学家距火车站x千米,由题意,
得x÷5x÷20+2.
解这个方程,得x=20.
答:小明同学家距火车站20千米,
故答案为:20.
【点评】本题主要考查了一元一次方程的应用,掌握“路程=速度×时间”是解决本题的关键.
15.(2分)如图,长方形ABCD中,AB=5厘米,BC=3厘米,把长方形ABCD绕顶点B顺时针转动,使点A落在点A′处,点C落在点C′处,且点A、B、C′三点在一条直线上,则A点和C点所经过的路程之比为 5:3 .
【考点】比的应用.
【专题】实数;运算能力;应用意识.
【答案】5:3.
【分析】分别计算A点和C点所经过的路程,然后求出比值即可.
【解答】解:点A经过的路程为:,
点C经过的路程为:,
∴A点和C点所经过的路程之比为:5:3.
故答案为:5:3.
【点评】本题考查了比的应用,解题的关键根据题意计算点A和点C经过的路程.
16.(2分)我国木雕艺术历史悠久.如图1为一木雕的实物图,如图2此木雕可以近似地看作扇环,其中OC长为0.2米,AC长为0.5米,∠COD为100°,则木雕的面积(镂空部分忽略不计)为 平方米.(结果保留π)
【考点】扇形的面积.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】根据扇形的面积公式计算即可.
【解答】解:∵OC=0.2米,AC=0.5米,∠COD=100°,
∴R=OC+AC=0.7(米),r=OC=0.2(米),
∴S木雕=S扇形AOB﹣S扇形COD
(R2﹣r2)
(0.72﹣0.22)
.
故答案为:.
【点评】本题考查扇形的面积,掌握扇形的面积公式是本题的关键.
三.解答题(共1小题,满分30分,每小题30分)
17.(30分)计算:
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)解方程:.
【考点】解一元一次方程;分数的混合运算;小数的运算.
【专题】实数;一次方程(组)及应用;运算能力.
【答案】(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)x=1.
【分析】(1)分别计算整数和分数部分,再合并;
(2)将带分数化为假分数,将除法转化为乘法,约分计算即可;
(3)先算除法,再算乘法,最后计算减法;
(4)将同分母分数相加,再计算;
(5)将小数化为分数,利用乘法分配律计算;
(6)将除法转化为乘法,再利用乘法分配律计算;
(7)先算括号内的,再算乘除,最后计算加法;
(8)利用等式的基本性质变形求解.
【解答】解:(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
;
(7)
;
(8),
,
,
,
x=1.
【点评】本题考查了分数的混合运算,解方程,解题的关键是掌握运算法则和运算顺序.
四.解答题(共7小题,满分50分)
18.(7分)如图,甲、乙、丙三个容器,甲为立方体,内壁的各条棱长为8厘米;乙为圆柱体,内壁高6厘米,内部底面半径为3厘米;丙是长方体,长12厘米,宽6厘米,高6厘米.现将甲容器盛满酒精,把甲容器内的酒精倒入与乙相同的2个容器,倒满后,把剩下的酒精倒入丙容器,求丙容器内酒精的高度(π取3,结果精确到0.1厘米).
【考点】认识立体图形;近似数和有效数字.
【专题】投影与视图;运算能力;应用意识.
【答案】2.4cm.
【分析】甲为立方体,已知其内壁的各条棱长相等,根据正方体体积公式计算其能装水的体积;根据圆柱的体积公式计算一个乙容器能装水的体积,甲容器能装水的体积﹣2×乙容器能装水的体积=还剩的水的体积;还剩的水的体积÷丙容器的底面积=丙容器内水的高度,至此不难得到算式,根据有理数混合运算的法则计算即可.
【解答】解:根据题意,得
(83﹣π×32×6×2)÷(12×6)≈2.4(cm).
∴丙容器内酒精的高度为2.4cm.
【点评】本题考查认识立体图形,掌握圆柱体积的计算公式是解题关键.
19.(7分)已知x、y为有理数,现规定一种新运算※,满足x※y=3y﹣2x.
(1)求2※3的值;
(2)化简a※(2a+3).
【考点】有理数的混合运算.
【专题】新定义;实数;运算能力.
【答案】(1)5;(2)4a+9.
【分析】(1)根据x※y=3y﹣2x,可以求得所求式子的值;
(2)根据x※y=3y﹣2x,可以将所求式子化简.
【解答】解:(1)∵x※y=3y﹣2x,
∴2※3
=3×3﹣2×2
=9﹣4
=5;
(2)∵x※y=3y﹣2x,
∴a※(2a+3)
=3(2a+3)﹣2a
=6a+9﹣2a
=4a+9.
【点评】本题考查有理数的混合运算、新运算,解答本题的关键是会用新运算解答问题.
20.(7分)实验小学购进鲜花150盆,其中摆放在大门两旁,其余的按2:3分别摆在教学楼和实验楼前,教学楼和实验楼前各放了多少盆鲜花?
【考点】分数混合运算的应用.
【专题】实数;运算能力.
【答案】教学楼前放了36盆,实验楼前放了54盆.
【分析】先求出剩下的月季花盆数,再根据比与分数的关系,求出放在教学楼前的盆数占余下盆数的,放在实验楼前的占余下盆数的,再根据分数乘法的意义列式解答.
【解答】解;
=90(盆);
(盆);
(盆);
答:教学楼前放了36盆,实验楼前放了54盆.
【点评】本题考查分数混合运算的应用,关键是求出余下的盆数,再根据按比例分配的知识进行解答.
21.(7分)A、B两地相距900米.甲乙二人同时从A地前往B地,甲每分钟行70米,乙每分钟行50米,甲到达B地后马上返回,与乙在途中相遇,两人从出发到相遇一共用了多少时间?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】15分钟.
【分析】设两人从出发到相遇一共用了x分钟,根据题意可知两人一共行了(900×2)米,利用路程=速度×时间,即可得出关于x的一元一次方程,解之即可得出结论.
【解答】解:设两人从出发到相遇一共用了x分钟,
依题意得:(70+50)x=900×2,
解得:x=15.
答:两人从出发到相遇一共用了15分钟.
【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
22.(7分)要在规定天数内修筑一段公路,若让甲队单独修筑,则正好在规定天数内按期完成;若让乙队单独修筑,则要比规定天数多8天才完成.现在由乙队单独修筑其中一小段,用去了规定时间的一半,然后甲队接着单独修筑2天,这段公路还有一半未修筑.若让两队共同再修筑2天,能否完成任务?
【考点】分式方程的应用.
【专题】分式方程及应用;运算能力;推理能力;应用意识.
【答案】若让两队再共同修筑2天,不能完成任务.
【分析】设甲队x天完成任务,则乙队(x+8)天完成任务,由题意:利用乙队单独修筑其中的一小段,用去了规定时间的一半,然后由甲队单独修筑2天,这段公路还有一半没有修筑,列出分式方程,解方程,进而得出答案.
【解答】解:设甲队x天完成任务,则乙队(x+8)天完成任务,
由题意得:,
解得:x=8,
检验得:x=8是原方程的根,
则2×(),
答:若让两队再共同修筑2天,不能完成任务.
【点评】此题主要考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
23.(7分)列一元一次方程解应用题:一列动车匀速行驶,完全通过一条长600米的隧道需要25秒的时间,隧道顶上有一盏灯,垂直向下发光,灯光照在动车上的时间是10秒,求这列动车的长度?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】火车的长度为400米.
【分析】根据题意可知:(隧道长度+火车长度)÷25=火车长度÷10,从而可以列出相应的方程,然后求解即可.
【解答】解:设火车的长度为x米,
,
解得x=400,
答:火车的长度为400米.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
24.(8分)学校要修建一个圆柱形的水池,在比例尺是1:200的设计图纸上,水池的半径为3厘米,深为2厘米.
(1)按图施工,这个水池的实际应该挖多少米深?
(2)按图施工,这个水池的能装下多少立方米的水?
(3)为了加固和美观,施工时给水池底部和水池壁都铺了水泥,且平均厚度是10厘米,然后再用油漆将新铺水泥的表面粉刷一遍,请问粉刷部分的面积是多少平方米?(结果保留一位小数)
【考点】几何体的表面积;比例尺;圆柱的表面积;圆柱的体积;近似数和有效数字.
【专题】线段、角、相交线与平行线;运算能力.
【答案】(1)这个水池的实际应该挖4米深;(2)这个水池的能装下452.16立方米的水;(2)粉刷部分的面积是253.8平方米.
【分析】(1)首先根据实际距离=图上距离÷比例尺,求出实际的半径和高,然后换算成用米作单位.
(2)根据圆柱的容积公式:V=πr2h,把数据代入公式解答.
(3)根据题意可知,刷漆的底面半径比原来水池的半径少10厘米(0.1米),水池内壁也就是圆柱的内侧面的高比原来水池的高减少了10厘米(0.1米),根据圆柱的侧面积公式:S=2πrh,圆的面积公式:S=πr2,把数据代入公式解答.
【解答】解:(1)实际半径:33×200=600(厘米),
600厘米=6米.
实际高:22×200=400(厘米)
400厘米=4米,
答:这个水池的实际应该挖4米深.
(2)3.14×62×4
=3.14×36×4
=113.04×4
=452.16(立方米).
答:这个水池的能装下452.16立方米的水.
(3)10厘米=0.1米
3.14×(6﹣0.1)×2×(4﹣0.1)+3.14×(6﹣0.1)2
=3.14×5.9×2×3.9+3.14×5.92
=37.052×3.9+3.14×34.81
=144.5028+109.3
=253.8028(平方米)
≈253.8(平方米)
答:粉刷部分的面积是253.8平方米.
【点评】本题主要考查的目的是理解掌握比例尺的意义及应用,圆柱的容积公式、圆柱的表面积公式的灵活运用,关键是熟记公式.
考点卡片
1.有理数大小比较
(1)有理数的大小比较
比较有理数的大小可以利用数轴,他们从右到左的顺序,即从大到小的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.
(2)有理数大小比较的法则:
①正数都大于0;
②负数都小于0;
③正数大于一切负数;
④两个负数,绝对值大的其值反而小.
【规律方法】有理数大小比较的三种方法
1.法则比较:正数都大于0,负数都小于0,正数大于一切负数.两个负数比较大小,绝对值大的反而小.
2.数轴比较:在数轴上右边的点表示的数大于左边的点表示的数.
3.作差比较:
若a﹣b>0,则a>b;
若a﹣b<0,则a<b;
若a﹣b=0,则a=b.
2.有理数的除法
(1)有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数,即:a÷b=a (b≠0)
(2)方法指引:
(1)两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
(2)有理数的除法要分情况灵活选择法则,若是整数与整数相除一般采用“同号得正,异号得负,并把绝对值相除”.如果有了分数,则采用“除以一个不等于0的数,等于乘这个数的倒数”,再约分.乘除混合运算时一定注意两个原则:①变除为乘,②从左到右.
3.有理数的混合运算
(1)有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
【规律方法】有理数混合运算的四种运算技巧
1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.
2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.
3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.
4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.
4.近似数和有效数字
(1)有效数字:从一个数的左边第一个不是0的数字起到末位数字止,所有的数字都是这个数的有效数字.
(2)近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.
(3)规律方法总结:
“精确到第几位”和“有几个有效数字”是精确度的两种常用的表示形式,它们实际意义是不一样的,前者可以体现出误差值绝对数的大小,而后者往往可以比较几个近似数中哪个相对更精确一些.
5.解一元一次方程
(1)解一元一次方程的一般步骤:
去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.
(2)解一元一次方程时先观察方程的形式和特点,若有分母一般先去分母;若既有分母又有括号,且括号外的项在乘括号内各项后能消去分母,就先去括号.
(3)在解类似于“ax+bx=c”的方程时,将方程左边,按合并同类项的方法并为一项即(a+b)x=c.使方程逐渐转化为ax=b的最简形式体现化归思想.将ax=b系数化为1时,要准确计算,一弄清求x时,方程两边除以的是a还是b,尤其a为分数时;二要准确判断符号,a、b同号x为正,a、b异号x为负.
6.一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价﹣进价,利润率100%);(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度﹣水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
7.分式方程的应用
1、列分式方程解应用题的一般步骤:设、列、解、验、答.
必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.
2、要掌握常见问题中的基本关系,如行程问题:速度=路程时间;工作量问题:工作效率=工作量工作时间
等等.
列分式方程解应用题一定要审清题意,找相等关系是着眼点,要学会分析题意,提高理解能力.
8.函数的图象
函数的图象定义
对于一个函数,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.
注意:①函数图形上的任意点(x,y)都满足其函数的解析式;②满足解析式的任意一对x、y的值,所对应的点一定在函数图象上;③判断点P(x,y)是否在函数图象上的方法是:将点P(x,y)的x、y的值代入函数的解析式,若能满足函数的解析式,这个点就在函数的图象上;如果不满足函数的解析式,这个点就不在函数的图象上..
9.认识立体图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
(3)重点和难点突破:
结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.能区分立体图形与平面图形,立体图形占有一定空间,各部分不都在同一平面内.
10.几何体的表面积
(1)几何体的表面积=侧面积+底面积(上、下底的面积和)
(2)常见的几种几何体的表面积的计算公式
①圆柱体表面积:2πR2+2πRh (R为圆柱体上下底圆半径,h为圆柱体高)
②圆锥体表面积:πr2(r为圆锥体底面圆半径,h为其高,n为圆锥侧面展开图中扇形的圆心角)
③长方体表面积:2(ab+ah+bh) (a为长方体的长,b为长方体的宽,h为长方体的高)
④正方体表面积:6a2(a为正方体棱长)
11.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质.分数的基本性质是约分和通分的理论依据.
12.分数的除法
分数除法是分数乘法的逆行运算(逆运算).分数除法的计算法则为:甲数除以乙数(0除外),等于甲数乘乙数的倒数.分数除法的结果能约分的要约分.
13.分数的混合运算
分数的混合运算可以分为这样2种:一种是同级运算,只包括加减或者是只有乘除的混合运算,像这样的混合运算,自然是从左往右算;一种是异级运算,加减乘除同时存在,甚至是包括小括号的,而像这样的运算自然是先算高级,再算低级,也就是没有括号的时候,先算乘除,后算加减,如果有括号先算括号.而混合运算,其实是建立在四则运算的每一个单项里,也就是分数加、减、乘、除分别怎么算.
14.分数混合运算的应用
分数的混合运算的应用包括两个部分的内容,第一是对整个应用题目信息的提取和分析得出计算的方法和分析的结果,其次是在计算的过程当中需要如何进行简便快速的运算,那么也是大家需要掌握的第二个重点问题.
15.小数的运算
在一个算式中,含有加、减、乘、除四种运算中两种或两种以上运算的,称为四则运算.运算中的数字是小数时叫做小数四则运算.法则 同级运算时,从左到右依次计算;两级运算时,先算乘除,再算加减.
16.比的基本性质
“比的基本性质:比的前项和后项同时乘或除以一个不为0的数,比值不变.最简比的前项和后项互质,且比的前项、后项都为整数.比值通常用整数表示,也可以用分数或小数表示.比的后项不能为0.比的后项乘以比值等于比的前项.比的前项除以后项等于比值.”
17.比的应用
1、比的第一种应用:已知两个或几个数量的和,这两个或几个数量的比,求这两个或者几个数量是多少?2、比的第二种应用:已知一个数量是多少,两个或几个数的比,求另外几个数量是多少?3、比的第三种应用:已知两个数量的差,两个或几个数的比,求这两个或者几个数量是多少?
18.比例尺
“比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比.公式为:比例尺=图上距离与实际距离的比.”
19.百分数的互化
1.百分比化成数值:百分比要换成数值就是把数直接除以100,如10%=10÷100=0.1.2.数值化成百分比:数值要加个百分比单位,就是把数值乘以100,如0.2=0.2x100%=20%.百分数通常不写成分数的形式,而采用百分号(%)来表示,如41%,1%等.
20.百分数的应用
超市卖货中的打折(折扣)问题,如一件上衣400元,现八折(80%)出售.成数问题,如这次小麦收成是上次的二成(20%).事物配制问题:如水占8伤,药占水的20%等.
21.扇形的面积
面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n°πr2/360°.如果其顶角采用弧度单位,则可简化为半径乘弧长乘1/2,弧长=半径×弧度)
22.圆柱的表面积
圆柱的表面积=侧面积+两个底面积(S表=S侧+2S底).
23.圆柱的体积
圆柱体积公式是用于计算圆柱体体积的公式,表达式为V=π*r2*h.
24.圆锥的体积
一个圆锥所占空间的大小,叫做这个圆锥的体积.一个圆锥的体积等于与它等底等高的圆柱的体积的三分之一,V圆锥=1/3Sh(S为圆锥的底面积,h为圆锥的高),圆锥底面积S=πR2(R为圆锥底面圆的半径.
2024—2025学年上学期福建初中数学七年级开学模拟试卷2
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)在5:7中,如果比的后项加上7,要使比值不变,前项应( )
A.加上7 B.乘7 C.乘2 D.加2
2.(2分)比﹣2小的数是( )
A.﹣3 B.﹣1 C.0 D.1
3.(2分)一根红色电线和一根蓝色电线一样长,红的剪去,蓝的剪去米,红的剩下的比蓝的短,原来这两根电线( )1米.
A.大于 B.小于 C.等于 D.都有可能
4.(2分)把一个长为2毫米的零件画在图纸上,在图纸上量得这个零件的长是2分米,则这幅图的比例尺是( )
A.1:100 B.1:1 C.100:1 D.100
5.(2分)张老师在化学实验室做实验时,将一杯100℃的开水放在石棉网上自然冷却至室温.水温T(℃)与时间t(min)的对应关系如图所示.根据图中所显示的信息,下列说法错误的是( )
A.水温从100℃逐渐下降到35℃时用了6min
B.当t=20时,水温是10℃
C.水温随时间的增加而降低
D.当0<t<10时,水温下降速度逐渐变慢
6.(2分)图中,可以表示计算过程的是( )
A. B.
C. D.
7.(2分)一件商品按七五折出售,这件商品降价了( )
A.7.5% B.75% C.25% D.2.5%
8.(2分)一个圆柱和一个圆锥的底面积相等,圆柱的高是圆锥高的2倍,则圆锥的体积是圆柱体积的( )
A. B. C. D.2倍
9.(2分)计算:24÷(﹣8)=( )
A.3 B.﹣3 C. D.
10.(2分)十个棱长为a的正方体摆放成如图的形状,这个图形的表面积是( )
A.36a2 B.36a C.6a2 D.30a2
二.填空题(共6小题,满分20分)
11.(6分)一根绳子减掉米还剩15米,则这根绳子的原长为 米.
12.(4分)15: =9÷24= %.
13.(4分)把400元存入银行,存期为5年,年利率为8.28%,到期时利息为 元.
14.(2分)小明同学以5千米/时的速度前进,可以及时从家到火车站,走了全程的后,他搭上了速度是20千米/时的汽车,因此,比预计的时间早2小时到达火车站,则他家距火车站 千米.
15.(2分)如图,长方形ABCD中,AB=5厘米,BC=3厘米,把长方形ABCD绕顶点B顺时针转动,使点A落在点A′处,点C落在点C′处,且点A、B、C′三点在一条直线上,则A点和C点所经过的路程之比为 .
16.(2分)我国木雕艺术历史悠久.如图1为一木雕的实物图,如图2此木雕可以近似地看作扇环,其中OC长为0.2米,AC长为0.5米,∠COD为100°,则木雕的面积(镂空部分忽略不计)为 平方米.(结果保留π)
三.解答题(共1小题,满分30分,每小题30分)
17.(30分)计算:
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)解方程:.
四.解答题(共7小题,满分50分)
18.(7分)如图,甲、乙、丙三个容器,甲为立方体,内壁的各条棱长为8厘米;乙为圆柱体,内壁高6厘米,内部底面半径为3厘米;丙是长方体,长12厘米,宽6厘米,高6厘米.现将甲容器盛满酒精,把甲容器内的酒精倒入与乙相同的2个容器,倒满后,把剩下的酒精倒入丙容器,求丙容器内酒精的高度(π取3,结果精确到0.1厘米).
19.(7分)已知x、y为有理数,现规定一种新运算※,满足x※y=3y﹣2x.
(1)求2※3的值;
(2)化简a※(2a+3).
20.(7分)实验小学购进鲜花150盆,其中摆放在大门两旁,其余的按2:3分别摆在教学楼和实验楼前,教学楼和实验楼前各放了多少盆鲜花?
21.(7分)A、B两地相距900米.甲乙二人同时从A地前往B地,甲每分钟行70米,乙每分钟行50米,甲到达B地后马上返回,与乙在途中相遇,两人从出发到相遇一共用了多少时间?
22.(7分)要在规定天数内修筑一段公路,若让甲队单独修筑,则正好在规定天数内按期完成;若让乙队单独修筑,则要比规定天数多8天才完成.现在由乙队单独修筑其中一小段,用去了规定时间的一半,然后甲队接着单独修筑2天,这段公路还有一半未修筑.若让两队共同再修筑2天,能否完成任务?
23.(7分)列一元一次方程解应用题:一列动车匀速行驶,完全通过一条长600米的隧道需要25秒的时间,隧道顶上有一盏灯,垂直向下发光,灯光照在动车上的时间是10秒,求这列动车的长度?
24.(8分)学校要修建一个圆柱形的水池,在比例尺是1:200的设计图纸上,水池的半径为3厘米,深为2厘米.
(1)按图施工,这个水池的实际应该挖多少米深?
(2)按图施工,这个水池的能装下多少立方米的水?
(3)为了加固和美观,施工时给水池底部和水池壁都铺了水泥,且平均厚度是10厘米,然后再用油漆将新铺水泥的表面粉刷一遍,请问粉刷部分的面积是多少平方米?(结果保留一位小数)
2024—2025学年上学期福建初中数学七年级开学模拟试卷2
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)在5:7中,如果比的后项加上7,要使比值不变,前项应( )
A.加上7 B.乘7 C.乘2 D.加2
【考点】比的基本性质.
【专题】实数;运算能力.
【答案】C
【分析】根据各个选项得出算式,再求出结果,最后根据求出的结果找出选项即可.
【解答】解:A.(5+7):(7+7)=12:14=6:7,和5:7不相等,故本选项不符合题意;
B.(5×7):(7+7)=35:14=5:2,和5:7不相等,故本选项不符合题意;
C.(5×2):(7+7)=10:14=5:7,故本选项符合题意;
D.(5+2):(7+7)=7:14=1:2,和5:7不相等,故本选项不符合题意.
故选:C.
【点评】本题考查了比的基本性质,能根据题意列出算式是解此题的关键.
2.(2分)比﹣2小的数是( )
A.﹣3 B.﹣1 C.0 D.1
【考点】有理数大小比较.
【专题】实数;数感.
【答案】A
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断出四个数中,比﹣2小的数是哪个数即可.
【解答】解:∵﹣3<﹣2<﹣1<0<1,
∴比﹣2小的数是﹣3.
故选:A.
【点评】此题主要考查了有理数大小比较,熟记有理数大小比较的法则是解答本题的关键.
3.(2分)一根红色电线和一根蓝色电线一样长,红的剪去,蓝的剪去米,红的剩下的比蓝的短,原来这两根电线( )1米.
A.大于 B.小于 C.等于 D.都有可能
【考点】分数的混合运算.
【专题】实数;运算能力.
【答案】A
【分析】根据分数乘法的意义解答即可.
【解答】解:假设原来这两根电线的长度为1米,则红的剪去,剩余米;蓝的剪去米,剩余米,这不符合题目中的“红的剩下的比蓝的短”的要求;
如果原来这两根电线的长度都大于1米,则红的剪去就大于米,所以红的剩下的比蓝的短,符合题意.
故选:A.
【点评】本题考查了分数的混合运算,掌握分数乘法的意义是解答本题的关键.
4.(2分)把一个长为2毫米的零件画在图纸上,在图纸上量得这个零件的长是2分米,则这幅图的比例尺是( )
A.1:100 B.1:1 C.100:1 D.100
【考点】比例尺.
【专题】尺规作图;数据分析观念.
【答案】C
【分析】根据图上距离、实际距离和比例尺的关系得出结论即可.
【解答】解:2分米=200毫米,
比例尺为200:2=100:1,
故选:C.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况.
5.(2分)张老师在化学实验室做实验时,将一杯100℃的开水放在石棉网上自然冷却至室温.水温T(℃)与时间t(min)的对应关系如图所示.根据图中所显示的信息,下列说法错误的是( )
A.水温从100℃逐渐下降到35℃时用了6min
B.当t=20时,水温是10℃
C.水温随时间的增加而降低
D.当0<t<10时,水温下降速度逐渐变慢
【考点】函数的图象.
【专题】函数及其图象;推理能力;应用意识.
【答案】C
【分析】根据图象逐项判断即可.
【解答】解:当T=100时,t=0;
当T=35时,t=6;
∴水温从100℃逐渐下降到35℃时用了6﹣0=6(min).
故A正确,不符合题意.
当t=20时,T=10,
故B正确,不符合题意.
当0≤t≤18时,T随t的增加而减小;
当t>18时,T不随t的增加而变化,恒为室温10℃.
故C不正确,符合题意.
当0<t<10时,曲线上各点的陡峭程度变得越来越小,
∴水温下降速度逐渐变慢.
故D正确,不符合题意.
故选:C.
【点评】本题考查函数的图象,这部分内容非常重要,一定要具备从图象上获取有用信息的能力.
6.(2分)图中,可以表示计算过程的是( )
A. B.
C. D.
【考点】分数的除法.
【专题】实数;数感.
【答案】D
【分析】根据图所表示的意义逐项进行分析即可.
【解答】解:由题可知,
A、阴影部分表示把单位“1”平均分成5份,再取其中的3份,用分数表示为,不符合题意;
B、阴影部分表示把单位“1”平均分成4份,再取其中的3份,用分数表示为,不符合题意;
C、阴影部分表示把单位“1”平均分成20份,再取其中的3份,用分数表示为,不符合题意;
D、阴影部分表示把单位“1”平均分成5份,再取其中的3份,用分数表示为,再把平均分成4份,取其中的1份,与算式4意义相同,符合题意.
故选:D.
【点评】本题考查分数的除法,能够根据图分析是解题的关键.
7.(2分)一件商品按七五折出售,这件商品降价了( )
A.7.5% B.75% C.25% D.2.5%
【考点】百分数的应用.
【专题】计算题;实数;运算能力;应用意识.
【答案】C
【分析】读懂题意,七五折出售,就是原价的75%,降价就是原价的1﹣75%.
【解答】解:1﹣75%=25%,
答:这件商品降价了25%.
故选:C.
【点评】本题考查了百分数的应用,解题的关键是理解打折的含义.
8.(2分)一个圆柱和一个圆锥的底面积相等,圆柱的高是圆锥高的2倍,则圆锥的体积是圆柱体积的( )
A. B. C. D.2倍
【考点】圆锥的体积;圆柱的体积.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力;推理能力.
【答案】C
【分析】由一个圆柱和一个圆锥的底面积相等,可设圆柱和圆锥的底面积为S,由圆柱的高是圆锥高的2倍,可设圆锥的高为h,圆柱的高为2h,根据圆柱与圆锥的体积公式,分别求出它们的体积,利用比的意义,即可求解.
【解答】解:设圆柱和圆锥的底面积为S,设圆锥的高为h,圆柱的高为2h,
圆柱的体积=S×2h=2Sh,圆锥的体积,
则圆锥的体积是圆柱体积的比是:,
答:圆锥的体积是圆柱体积的.
故选:C.
【点评】本题考查了圆柱与圆锥的体积计算以及比的意义的应用,灵活应用圆柱与圆锥的体积计算公式是解题的关键.
9.(2分)计算:24÷(﹣8)=( )
A.3 B.﹣3 C. D.
【考点】有理数的除法.
【专题】计算题;实数;运算能力.
【答案】B
【分析】先确定商的符号,再确定商的绝对值.
【解答】解;24÷(﹣8)=﹣3.
故选:B.
【点评】本题主要考查了有理数的运算,掌握有理数的除法法则是解决本题的关键.
10.(2分)十个棱长为a的正方体摆放成如图的形状,这个图形的表面积是( )
A.36a2 B.36a C.6a2 D.30a2
【考点】几何体的表面积;认识立体图形.
【专题】线段、角、相交线与平行线;空间观念.
【答案】A
【分析】先数出每个面的正方形的个数,然后加起来求出表面积即可.
【解答】解:由题意可得该图形的表面积为各个面的小正方形的面积之和,
∴该几何体前后左右上下各都有6个小正方形,共36个小正方形,
∵小正方体的棱长为 a,
∴该图形的表面积为36a2,
故选:A.
【点评】本题主要考查正方形的面积公式,关键是要准确数出图形外表面一共有几个正方形.
二.填空题(共6小题,满分20分)
11.(6分)一根绳子减掉米还剩15米,则这根绳子的原长为 15 米.
【考点】分数混合运算的应用.
【专题】计算题;实数;运算能力;应用意识.
【答案】15.
【分析】根据一根绳子减掉米还剩15米,则这根绳子的原长为15,然后计算即可.
【解答】解:由题意可得,
这根绳子的原长为:15=15(米),
故答案为:15.
【点评】本题考查分数混合运算的应用,解答本题的关键是明确题意,列出相应的算式.
12.(4分)15: 40 =9÷24= 37.5 %.
【考点】百分数的互化;分数的基本性质.
【专题】实数;运算能力.
【答案】3,40,37.5.
【分析】根据分数的基本性质进行解题即可.
【解答】解:9÷240.375=37.5%.
故答案为:3,40,37.5.
【点评】本题考查百分数的互化和分数的基本性质,熟练掌握相关的知识点是解题的关键.
13.(4分)把400元存入银行,存期为5年,年利率为8.28%,到期时利息为 165.6 元.
【考点】百分数的应用.
【专题】实数;运算能力;应用意识.
【答案】165.6.
【分析】根据“利息=本金×利率×存期”列出算式,即可求解.
【解答】解:根据“利息=本金×利率×存期”可得,
400×8.28%×5
=33.12×5
=165.6(元).
∴到期时利息为165.6元.
故答案为:165.6.
【点评】本题考查有理数的混合运算,解答本题是明确“利息=本金×利率×存期”.
14.(2分)小明同学以5千米/时的速度前进,可以及时从家到火车站,走了全程的后,他搭上了速度是20千米/时的汽车,因此,比预计的时间早2小时到达火车站,则他家距火车站 20 千米.
【考点】分数混合运算的应用.
【专题】应用题;一次方程(组)及应用;运算能力.
【答案】20.
【分析】根据“小明从家到火车站的时间=小明走全程的时间+小明做汽车走全程的时间+早到的时间”列出方程,并求解即可.
【解答】解:小明同学家距火车站x千米,由题意,
得x÷5x÷20+2.
解这个方程,得x=20.
答:小明同学家距火车站20千米,
故答案为:20.
【点评】本题主要考查了一元一次方程的应用,掌握“路程=速度×时间”是解决本题的关键.
15.(2分)如图,长方形ABCD中,AB=5厘米,BC=3厘米,把长方形ABCD绕顶点B顺时针转动,使点A落在点A′处,点C落在点C′处,且点A、B、C′三点在一条直线上,则A点和C点所经过的路程之比为 5:3 .
【考点】比的应用.
【专题】实数;运算能力;应用意识.
【答案】5:3.
【分析】分别计算A点和C点所经过的路程,然后求出比值即可.
【解答】解:点A经过的路程为:,
点C经过的路程为:,
∴A点和C点所经过的路程之比为:5:3.
故答案为:5:3.
【点评】本题考查了比的应用,解题的关键根据题意计算点A和点C经过的路程.
16.(2分)我国木雕艺术历史悠久.如图1为一木雕的实物图,如图2此木雕可以近似地看作扇环,其中OC长为0.2米,AC长为0.5米,∠COD为100°,则木雕的面积(镂空部分忽略不计)为 平方米.(结果保留π)
【考点】扇形的面积.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】根据扇形的面积公式计算即可.
【解答】解:∵OC=0.2米,AC=0.5米,∠COD=100°,
∴R=OC+AC=0.7(米),r=OC=0.2(米),
∴S木雕=S扇形AOB﹣S扇形COD
(R2﹣r2)
(0.72﹣0.22)
.
故答案为:.
【点评】本题考查扇形的面积,掌握扇形的面积公式是本题的关键.
三.解答题(共1小题,满分30分,每小题30分)
17.(30分)计算:
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)解方程:.
【考点】解一元一次方程;分数的混合运算;小数的运算.
【专题】实数;一次方程(组)及应用;运算能力.
【答案】(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)x=1.
【分析】(1)分别计算整数和分数部分,再合并;
(2)将带分数化为假分数,将除法转化为乘法,约分计算即可;
(3)先算除法,再算乘法,最后计算减法;
(4)将同分母分数相加,再计算;
(5)将小数化为分数,利用乘法分配律计算;
(6)将除法转化为乘法,再利用乘法分配律计算;
(7)先算括号内的,再算乘除,最后计算加法;
(8)利用等式的基本性质变形求解.
【解答】解:(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
;
(7)
;
(8),
,
,
,
x=1.
【点评】本题考查了分数的混合运算,解方程,解题的关键是掌握运算法则和运算顺序.
四.解答题(共7小题,满分50分)
18.(7分)如图,甲、乙、丙三个容器,甲为立方体,内壁的各条棱长为8厘米;乙为圆柱体,内壁高6厘米,内部底面半径为3厘米;丙是长方体,长12厘米,宽6厘米,高6厘米.现将甲容器盛满酒精,把甲容器内的酒精倒入与乙相同的2个容器,倒满后,把剩下的酒精倒入丙容器,求丙容器内酒精的高度(π取3,结果精确到0.1厘米).
【考点】认识立体图形;近似数和有效数字.
【专题】投影与视图;运算能力;应用意识.
【答案】2.4cm.
【分析】甲为立方体,已知其内壁的各条棱长相等,根据正方体体积公式计算其能装水的体积;根据圆柱的体积公式计算一个乙容器能装水的体积,甲容器能装水的体积﹣2×乙容器能装水的体积=还剩的水的体积;还剩的水的体积÷丙容器的底面积=丙容器内水的高度,至此不难得到算式,根据有理数混合运算的法则计算即可.
【解答】解:根据题意,得
(83﹣π×32×6×2)÷(12×6)≈2.4(cm).
∴丙容器内酒精的高度为2.4cm.
【点评】本题考查认识立体图形,掌握圆柱体积的计算公式是解题关键.
19.(7分)已知x、y为有理数,现规定一种新运算※,满足x※y=3y﹣2x.
(1)求2※3的值;
(2)化简a※(2a+3).
【考点】有理数的混合运算.
【专题】新定义;实数;运算能力.
【答案】(1)5;(2)4a+9.
【分析】(1)根据x※y=3y﹣2x,可以求得所求式子的值;
(2)根据x※y=3y﹣2x,可以将所求式子化简.
【解答】解:(1)∵x※y=3y﹣2x,
∴2※3
=3×3﹣2×2
=9﹣4
=5;
(2)∵x※y=3y﹣2x,
∴a※(2a+3)
=3(2a+3)﹣2a
=6a+9﹣2a
=4a+9.
【点评】本题考查有理数的混合运算、新运算,解答本题的关键是会用新运算解答问题.
20.(7分)实验小学购进鲜花150盆,其中摆放在大门两旁,其余的按2:3分别摆在教学楼和实验楼前,教学楼和实验楼前各放了多少盆鲜花?
【考点】分数混合运算的应用.
【专题】实数;运算能力.
【答案】教学楼前放了36盆,实验楼前放了54盆.
【分析】先求出剩下的月季花盆数,再根据比与分数的关系,求出放在教学楼前的盆数占余下盆数的,放在实验楼前的占余下盆数的,再根据分数乘法的意义列式解答.
【解答】解;
=90(盆);
(盆);
(盆);
答:教学楼前放了36盆,实验楼前放了54盆.
【点评】本题考查分数混合运算的应用,关键是求出余下的盆数,再根据按比例分配的知识进行解答.
21.(7分)A、B两地相距900米.甲乙二人同时从A地前往B地,甲每分钟行70米,乙每分钟行50米,甲到达B地后马上返回,与乙在途中相遇,两人从出发到相遇一共用了多少时间?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】15分钟.
【分析】设两人从出发到相遇一共用了x分钟,根据题意可知两人一共行了(900×2)米,利用路程=速度×时间,即可得出关于x的一元一次方程,解之即可得出结论.
【解答】解:设两人从出发到相遇一共用了x分钟,
依题意得:(70+50)x=900×2,
解得:x=15.
答:两人从出发到相遇一共用了15分钟.
【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
22.(7分)要在规定天数内修筑一段公路,若让甲队单独修筑,则正好在规定天数内按期完成;若让乙队单独修筑,则要比规定天数多8天才完成.现在由乙队单独修筑其中一小段,用去了规定时间的一半,然后甲队接着单独修筑2天,这段公路还有一半未修筑.若让两队共同再修筑2天,能否完成任务?
【考点】分式方程的应用.
【专题】分式方程及应用;运算能力;推理能力;应用意识.
【答案】若让两队再共同修筑2天,不能完成任务.
【分析】设甲队x天完成任务,则乙队(x+8)天完成任务,由题意:利用乙队单独修筑其中的一小段,用去了规定时间的一半,然后由甲队单独修筑2天,这段公路还有一半没有修筑,列出分式方程,解方程,进而得出答案.
【解答】解:设甲队x天完成任务,则乙队(x+8)天完成任务,
由题意得:,
解得:x=8,
检验得:x=8是原方程的根,
则2×(),
答:若让两队再共同修筑2天,不能完成任务.
【点评】此题主要考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
23.(7分)列一元一次方程解应用题:一列动车匀速行驶,完全通过一条长600米的隧道需要25秒的时间,隧道顶上有一盏灯,垂直向下发光,灯光照在动车上的时间是10秒,求这列动车的长度?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】火车的长度为400米.
【分析】根据题意可知:(隧道长度+火车长度)÷25=火车长度÷10,从而可以列出相应的方程,然后求解即可.
【解答】解:设火车的长度为x米,
,
解得x=400,
答:火车的长度为400米.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
24.(8分)学校要修建一个圆柱形的水池,在比例尺是1:200的设计图纸上,水池的半径为3厘米,深为2厘米.
(1)按图施工,这个水池的实际应该挖多少米深?
(2)按图施工,这个水池的能装下多少立方米的水?
(3)为了加固和美观,施工时给水池底部和水池壁都铺了水泥,且平均厚度是10厘米,然后再用油漆将新铺水泥的表面粉刷一遍,请问粉刷部分的面积是多少平方米?(结果保留一位小数)
【考点】几何体的表面积;比例尺;圆柱的表面积;圆柱的体积;近似数和有效数字.
【专题】线段、角、相交线与平行线;运算能力.
【答案】(1)这个水池的实际应该挖4米深;(2)这个水池的能装下452.16立方米的水;(2)粉刷部分的面积是253.8平方米.
【分析】(1)首先根据实际距离=图上距离÷比例尺,求出实际的半径和高,然后换算成用米作单位.
(2)根据圆柱的容积公式:V=πr2h,把数据代入公式解答.
(3)根据题意可知,刷漆的底面半径比原来水池的半径少10厘米(0.1米),水池内壁也就是圆柱的内侧面的高比原来水池的高减少了10厘米(0.1米),根据圆柱的侧面积公式:S=2πrh,圆的面积公式:S=πr2,把数据代入公式解答.
【解答】解:(1)实际半径:33×200=600(厘米),
600厘米=6米.
实际高:22×200=400(厘米)
400厘米=4米,
答:这个水池的实际应该挖4米深.
(2)3.14×62×4
=3.14×36×4
=113.04×4
=452.16(立方米).
答:这个水池的能装下452.16立方米的水.
(3)10厘米=0.1米
3.14×(6﹣0.1)×2×(4﹣0.1)+3.14×(6﹣0.1)2
=3.14×5.9×2×3.9+3.14×5.92
=37.052×3.9+3.14×34.81
=144.5028+109.3
=253.8028(平方米)
≈253.8(平方米)
答:粉刷部分的面积是253.8平方米.
【点评】本题主要考查的目的是理解掌握比例尺的意义及应用,圆柱的容积公式、圆柱的表面积公式的灵活运用,关键是熟记公式.
考点卡片
1.有理数大小比较
(1)有理数的大小比较
比较有理数的大小可以利用数轴,他们从右到左的顺序,即从大到小的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.
(2)有理数大小比较的法则:
①正数都大于0;
②负数都小于0;
③正数大于一切负数;
④两个负数,绝对值大的其值反而小.
【规律方法】有理数大小比较的三种方法
1.法则比较:正数都大于0,负数都小于0,正数大于一切负数.两个负数比较大小,绝对值大的反而小.
2.数轴比较:在数轴上右边的点表示的数大于左边的点表示的数.
3.作差比较:
若a﹣b>0,则a>b;
若a﹣b<0,则a<b;
若a﹣b=0,则a=b.
2.有理数的除法
(1)有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数,即:a÷b=a (b≠0)
(2)方法指引:
(1)两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
(2)有理数的除法要分情况灵活选择法则,若是整数与整数相除一般采用“同号得正,异号得负,并把绝对值相除”.如果有了分数,则采用“除以一个不等于0的数,等于乘这个数的倒数”,再约分.乘除混合运算时一定注意两个原则:①变除为乘,②从左到右.
3.有理数的混合运算
(1)有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
【规律方法】有理数混合运算的四种运算技巧
1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.
2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.
3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.
4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.
4.近似数和有效数字
(1)有效数字:从一个数的左边第一个不是0的数字起到末位数字止,所有的数字都是这个数的有效数字.
(2)近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.
(3)规律方法总结:
“精确到第几位”和“有几个有效数字”是精确度的两种常用的表示形式,它们实际意义是不一样的,前者可以体现出误差值绝对数的大小,而后者往往可以比较几个近似数中哪个相对更精确一些.
5.解一元一次方程
(1)解一元一次方程的一般步骤:
去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.
(2)解一元一次方程时先观察方程的形式和特点,若有分母一般先去分母;若既有分母又有括号,且括号外的项在乘括号内各项后能消去分母,就先去括号.
(3)在解类似于“ax+bx=c”的方程时,将方程左边,按合并同类项的方法并为一项即(a+b)x=c.使方程逐渐转化为ax=b的最简形式体现化归思想.将ax=b系数化为1时,要准确计算,一弄清求x时,方程两边除以的是a还是b,尤其a为分数时;二要准确判断符号,a、b同号x为正,a、b异号x为负.
6.一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价﹣进价,利润率100%);(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度﹣水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
7.分式方程的应用
1、列分式方程解应用题的一般步骤:设、列、解、验、答.
必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.
2、要掌握常见问题中的基本关系,如行程问题:速度=路程时间;工作量问题:工作效率=工作量工作时间
等等.
列分式方程解应用题一定要审清题意,找相等关系是着眼点,要学会分析题意,提高理解能力.
8.函数的图象
函数的图象定义
对于一个函数,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.
注意:①函数图形上的任意点(x,y)都满足其函数的解析式;②满足解析式的任意一对x、y的值,所对应的点一定在函数图象上;③判断点P(x,y)是否在函数图象上的方法是:将点P(x,y)的x、y的值代入函数的解析式,若能满足函数的解析式,这个点就在函数的图象上;如果不满足函数的解析式,这个点就不在函数的图象上..
9.认识立体图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
(3)重点和难点突破:
结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.能区分立体图形与平面图形,立体图形占有一定空间,各部分不都在同一平面内.
10.几何体的表面积
(1)几何体的表面积=侧面积+底面积(上、下底的面积和)
(2)常见的几种几何体的表面积的计算公式
①圆柱体表面积:2πR2+2πRh (R为圆柱体上下底圆半径,h为圆柱体高)
②圆锥体表面积:πr2(r为圆锥体底面圆半径,h为其高,n为圆锥侧面展开图中扇形的圆心角)
③长方体表面积:2(ab+ah+bh) (a为长方体的长,b为长方体的宽,h为长方体的高)
④正方体表面积:6a2(a为正方体棱长)
11.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质.分数的基本性质是约分和通分的理论依据.
12.分数的除法
分数除法是分数乘法的逆行运算(逆运算).分数除法的计算法则为:甲数除以乙数(0除外),等于甲数乘乙数的倒数.分数除法的结果能约分的要约分.
13.分数的混合运算
分数的混合运算可以分为这样2种:一种是同级运算,只包括加减或者是只有乘除的混合运算,像这样的混合运算,自然是从左往右算;一种是异级运算,加减乘除同时存在,甚至是包括小括号的,而像这样的运算自然是先算高级,再算低级,也就是没有括号的时候,先算乘除,后算加减,如果有括号先算括号.而混合运算,其实是建立在四则运算的每一个单项里,也就是分数加、减、乘、除分别怎么算.
14.分数混合运算的应用
分数的混合运算的应用包括两个部分的内容,第一是对整个应用题目信息的提取和分析得出计算的方法和分析的结果,其次是在计算的过程当中需要如何进行简便快速的运算,那么也是大家需要掌握的第二个重点问题.
15.小数的运算
在一个算式中,含有加、减、乘、除四种运算中两种或两种以上运算的,称为四则运算.运算中的数字是小数时叫做小数四则运算.法则 同级运算时,从左到右依次计算;两级运算时,先算乘除,再算加减.
16.比的基本性质
“比的基本性质:比的前项和后项同时乘或除以一个不为0的数,比值不变.最简比的前项和后项互质,且比的前项、后项都为整数.比值通常用整数表示,也可以用分数或小数表示.比的后项不能为0.比的后项乘以比值等于比的前项.比的前项除以后项等于比值.”
17.比的应用
1、比的第一种应用:已知两个或几个数量的和,这两个或几个数量的比,求这两个或者几个数量是多少?2、比的第二种应用:已知一个数量是多少,两个或几个数的比,求另外几个数量是多少?3、比的第三种应用:已知两个数量的差,两个或几个数的比,求这两个或者几个数量是多少?
18.比例尺
“比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比.公式为:比例尺=图上距离与实际距离的比.”
19.百分数的互化
1.百分比化成数值:百分比要换成数值就是把数直接除以100,如10%=10÷100=0.1.2.数值化成百分比:数值要加个百分比单位,就是把数值乘以100,如0.2=0.2x100%=20%.百分数通常不写成分数的形式,而采用百分号(%)来表示,如41%,1%等.
20.百分数的应用
超市卖货中的打折(折扣)问题,如一件上衣400元,现八折(80%)出售.成数问题,如这次小麦收成是上次的二成(20%).事物配制问题:如水占8伤,药占水的20%等.
21.扇形的面积
面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n°πr2/360°.如果其顶角采用弧度单位,则可简化为半径乘弧长乘1/2,弧长=半径×弧度)
22.圆柱的表面积
圆柱的表面积=侧面积+两个底面积(S表=S侧+2S底).
23.圆柱的体积
圆柱体积公式是用于计算圆柱体体积的公式,表达式为V=π*r2*h.
24.圆锥的体积
一个圆锥所占空间的大小,叫做这个圆锥的体积.一个圆锥的体积等于与它等底等高的圆柱的体积的三分之一,V圆锥=1/3Sh(S为圆锥的底面积,h为圆锥的高),圆锥底面积S=πR2(R为圆锥底面圆的半径.
同课章节目录
