2024—2025学年上学期长沙初中数学七年级开学模拟试卷1(含解析+知识卡片)
文档属性
| 名称 | 2024—2025学年上学期长沙初中数学七年级开学模拟试卷1(含解析+知识卡片) |  | |
| 格式 | docx | ||
| 文件大小 | 317.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 08:36:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024—2025学年上学期长沙初中数学七年级开学模拟试卷1
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下面的数中,与2022的和为0的是( )
A.2022 B.﹣2022 C. D.
2.(3分)2022年宁波舟山港完成货物吞吐量超12.5亿吨,连续14年位居全球第一.其中12.5亿用科学记数法表示为( )
A.12.5×108 B.1.25×109 C.0.125×109 D.1.25×108
3.(3分)下列各组数中,数值相等的是( )
A.﹣35与(﹣5)3 B.﹣35与(﹣3)5
C.﹣34与(﹣5)4 D.(﹣3×5)3与﹣3×53
4.(3分)下列各式中,与3x2y3是同类项的是( )
A.2x5 B.3x3y2 C.x2y3 D.y5
5.(3分)下列等式变形正确的是( )
A.若a=b,则a﹣3=3﹣b B.若ax=ay,则x=y
C.若a=b,则 D.若,则b=d
6.(3分)如图,OC⊥AB于点O,∠1=∠2,则图中互余的角有( )
A.1对 B.2对 C.3对 D.4对
7.(3分)某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
8.(3分)小红所在城市的居民用水实行“阶梯价格”收费,收费办法是:每户用水不超过20m3,每立方米水费x元;超过20m3,每立方米加收1.05元,小红家今年3月份用水28m3,缴纳水费89.6元,根据题意列出关于x的方程,正确的是( )
A.20x+8(x+1.05)=89.6
B.20x+8(x﹣1.05)=89.6
C.28(x+1.05)=89.6
D.28(x+1.05)﹣8×1.05=89.6
9.(3分)下列说法正确的是( )
A.连接两点的线段,叫做两点间的距离
B.射线OA与射线AO表示的是同一条射线
C.经过两点有一条直线,并且只有一条直线
D.从一点引出的两条直线所形成的图形叫做角
10.(3分)按一定规律排列的一列数依次为3,6,12,24,…,按此规律排列下去,这列数的第7个数是( )
A.96 B.124 C.192 D.234
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)淮北有一天的最低气温是﹣6℃,最高气温是12℃,这一天的最高气温与最低气温相差 度.
12.(3分)若平面内有点A、B、C、D,过其中任意两点画直线,可以画 条直线.
13.(3分)已知,2m﹣5n=﹣5,则代数式4m﹣10n的值为 .
14.(3分)钟表上显示10时36分,则此刻时针与分针的夹角的度数为 °.
15.(3分)将纸条照如图方式折一下,经测量∠ABC为30°,那么∠CBD= .
16.(3分)一组“数值转换机”按下面的程序计算,如果输入的数是10,那么输出的结果为19,要使输出的结果为13,则输入的最小正整数是 .
三.解答题(共9小题,满分72分,每小题8分)
17.(8分)计算:
(1)2﹣18
(2)﹣14﹣2×(﹣3)2÷||
18.(8分)解方程:2(x+2)+1=7﹣2(x﹣1).
19.(6分)(1)已知代数式3a﹣7b的值为﹣3,求代数式2(2a+b﹣1)+5(a﹣4b+1)﹣3b的值.
(2)先化简,再求值:﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2,其中a=2,b.
20.(6分)阅读下面材料,完成任务.
绝对值的几何意义指的是数轴上的点到原点的距离,例如|2|的几何意义是数轴上表示数2的点到原点之间的距离,我们可以理解为|2﹣0|,同理|7﹣3|的几何意义是数轴上表示数7的点与表示数3的点之间的距离.若出现|7+3|,则先对式子进行调整,得|7﹣(﹣3)|,其几何意义为数轴上表示数7的点与表示数﹣3的点之间的距离.
(1)|﹣1+5|的几何意义是数﹣1和数 的距离,故|﹣1+5|= .
(2)|x﹣2|+|x+3|的最小值是 .
(3)|x﹣2|+|x﹣1|+|x+3|的最小值是 .
21.(6分)如图,已知三点A、B、C,请用尺规作图完成.(保留作图痕迹,不要求写作法)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+AC.
22.(9分)甲、乙两家影院为刺激票房收入,五一期间均推出了优惠活动.
甲影院:3人以内(含3人)按原价购票,超出3人时,超出的人员购票打五折;乙影院:购票一律打八折.
若某电影在两家影院的原价都是60元一张票,小明同学一家人去看电影,若他们到甲、乙两家影院购票费用相同,请问他们一家总共多少人?
23.(9分)如图,在直线l上按指定方向依次取点A,B,C,D,且使AB:BC:CD=2:3:4.若AB的中点M与CD的中点N的距离是15cm,求AB的长.
24.(10分)阅读与理解:
定义:如果两个一元一次方程的解之和为1,我们就称这两个方程互为“美好方程”.
例如:方程2x﹣1=3的解为x=2,x+1=0解为x=﹣1,两个方程解之和为1,所以这两个方程互为“美好方程”.
(1)请判断方程4x﹣(x+5)=1与方程﹣2y﹣y=3是否互为“美好方程”;
(2)若关于x的方程与方程3x=x+4是互为“美好方程”,求m的值.
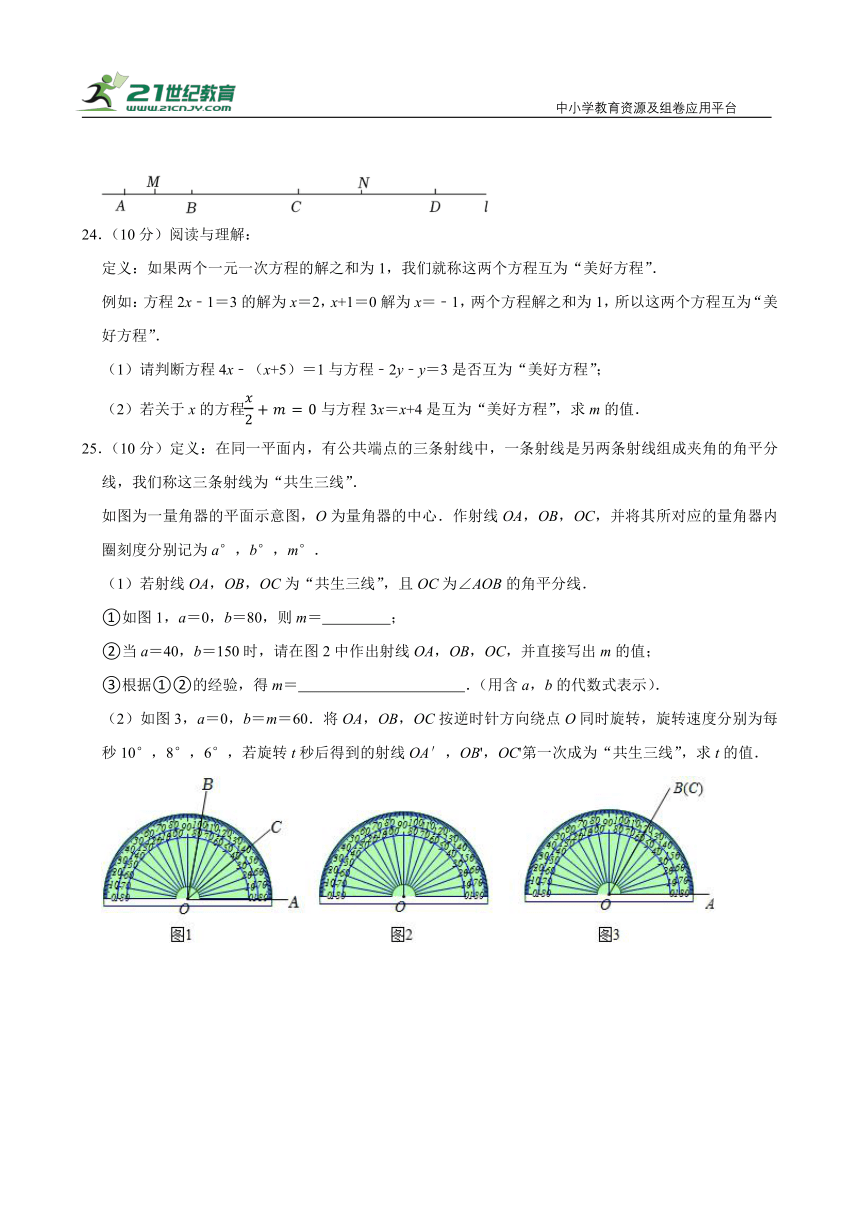
25.(10分)定义:在同一平面内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.
如图为一量角器的平面示意图,O为量角器的中心.作射线OA,OB,OC,并将其所对应的量角器内圈刻度分别记为a°,b°,m°.
(1)若射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线.
①如图1,a=0,b=80,则m= ;
②当a=40,b=150时,请在图2中作出射线OA,OB,OC,并直接写出m的值;
③根据①②的经验,得m= .(用含a,b的代数式表示).
(2)如图3,a=0,b=m=60.将OA,OB,OC按逆时针方向绕点O同时旋转,旋转速度分别为每秒10°,8°,6°,若旋转t秒后得到的射线OA′,OB',OC'第一次成为“共生三线”,求t的值.
2024—2025学年上学期长沙初中数学七年级开学模拟试卷1
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下面的数中,与2022的和为0的是( )
A.2022 B.﹣2022 C. D.
【考点】相反数.
【专题】计算题;实数;运算能力.
【答案】B
【分析】利用有理数的加法或互为相反数的定义计算并判断.
【解答】解:与2022的和为0的数是﹣2022,
故选:B.
【点评】本题考查了有理数的加法法则,解题的关键是掌握有理数的加法法则.
2.(3分)2022年宁波舟山港完成货物吞吐量超12.5亿吨,连续14年位居全球第一.其中12.5亿用科学记数法表示为( )
A.12.5×108 B.1.25×109 C.0.125×109 D.1.25×108
【考点】科学记数法—表示较大的数.
【专题】实数;数感.
【答案】B
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
【解答】解:12.5亿=1250000000=1.25×109.
故选:B.
【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
3.(3分)下列各组数中,数值相等的是( )
A.﹣35与(﹣5)3 B.﹣35与(﹣3)5
C.﹣34与(﹣5)4 D.(﹣3×5)3与﹣3×53
【考点】有理数的乘方;有理数的乘法.
【专题】实数;运算能力.
【答案】B
【分析】根据有理数的乘方、有理数的乘法法则解决此题.
【解答】解:A.根据有理数的乘方,﹣35=﹣243,(﹣5)3=﹣125,故﹣35≠(﹣5)3,那么A不符合题意.
B.根据有理数的乘方,﹣35=﹣243,(﹣3)5=﹣243,故﹣35=(﹣3)5,那么B符合题意.
C.根据有理数的乘方,﹣34=﹣81,(﹣5)4=625,那么﹣34≠(﹣5)4,那么C不符合题意.
D.根据有理数的乘法以及乘方,(﹣3×5)3=﹣27×53≠﹣3×53,那么D不符合题意.
故选:B.
【点评】本题主要考查有理数的乘方、有理数的乘法,熟练掌握有理数的乘方、有理数的乘法法则是解决本题的关键.
4.(3分)下列各式中,与3x2y3是同类项的是( )
A.2x5 B.3x3y2 C.x2y3 D.y5
【考点】同类项.
【专题】整式;数感;符号意识;模型思想.
【答案】C
【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,进行判断即可.
【解答】解:A、2x5与3x2y3不是同类项,故本选项错误;
B、3x3y2与3x2y3不是同类项,故本选项错误;
C、x2y3与3x2y3是同类项,故本选项正确;
D、y5与3x2y3不是同类项,故本选项错误;
故选:C.
【点评】本题考查了同类项的知识,解答本题的关键是理解同类项的定义.
5.(3分)下列等式变形正确的是( )
A.若a=b,则a﹣3=3﹣b B.若ax=ay,则x=y
C.若a=b,则 D.若,则b=d
【考点】等式的性质.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】根据等式的性质逐个判断即可.
【解答】解:A.∵a=b,
∴a﹣3=b﹣3,故本选项不符合题意;
B.当a=0时,由ax=ay不能推出x=y,故本选项不符合题意;
C.当c=0时,由a=b不能推出,故本选项不符合题意;
D.∵,
∴等式两边都乘c得:b=d,故本选项符合题意;
故选:D.
【点评】本题考查了等式的性质,能熟记等式的性质是解此题的关键,等式的性质1:等式的两边加(或减)同一个数(或式子),等式仍成立;等式的性质2:等式的两边乘同一个数,等式仍成立;等式的两边都除以同一个不等于0的数,等式仍成立.
6.(3分)如图,OC⊥AB于点O,∠1=∠2,则图中互余的角有( )
A.1对 B.2对 C.3对 D.4对
【考点】垂线;余角和补角.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】D
【分析】根据OC⊥AB于点O,可知∠1与∠AOD互为余角,∠2与∠COD互为余角,又因为∠1=∠2,则相互交换又多了两对互余角.
【解答】解:∵OC⊥AB,
∴∠1+∠AOD=90°,∠2+∠COE=90°,
即∠1与∠AOD互为余角,∠2与∠COE互为余角,
∵∠1=∠2,
∴∠1+∠COE=90°,∠2+∠AOD=90°,
即∠1与∠COE互为余角,∠2与∠AOD互为余角.
所以图中互余的角有4对.
故选:D.
【点评】本题考查了垂线的知识,解答本题的关键是根据垂直得出直角,继而找到互余的角.
7.(3分)某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
【考点】方向角.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】B
【分析】根据方位角的概念画出图形,再根据已知结合角的和差关系求解.
【解答】解:如图所示:
∵某人在A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,
∴∠BAD=40°,∠CAD=35°,
∴∠BAC=∠BAD+∠CAD=40°+35°=75°.
故选:B.
【点评】本题考查了方向角,解答此类题关键是需要从运动的角度,正确画出方位角,再结合角的和差关系求解.
8.(3分)小红所在城市的居民用水实行“阶梯价格”收费,收费办法是:每户用水不超过20m3,每立方米水费x元;超过20m3,每立方米加收1.05元,小红家今年3月份用水28m3,缴纳水费89.6元,根据题意列出关于x的方程,正确的是( )
A.20x+8(x+1.05)=89.6
B.20x+8(x﹣1.05)=89.6
C.28(x+1.05)=89.6
D.28(x+1.05)﹣8×1.05=89.6
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;应用意识.
【答案】A
【分析】利用总价=单价×数量,结合“阶梯价格”收费标准,即可得出关于x的一元一次方程,此题得解.
【解答】解:根据题意得:20x+(28﹣20)(x+1.05)=89.6,
即20x+8(x+1.05)=89.6.
故选:A.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
9.(3分)下列说法正确的是( )
A.连接两点的线段,叫做两点间的距离
B.射线OA与射线AO表示的是同一条射线
C.经过两点有一条直线,并且只有一条直线
D.从一点引出的两条直线所形成的图形叫做角
【考点】角的概念;直线、射线、线段;直线的性质:两点确定一条直线;两点间的距离.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】依据角的概念、射线的概念、直线的性质以及两点间的距离,即可得到正确结论.
【解答】解:A.连接两点的线段的长度,叫做两点间的距离,故本选项错误;
B.射线OA与射线AO表示的是不同的两条射线,故本选项错误;
C.经过两点有一条直线,并且只有一条直线,故本选项正确;
D.从一点引出的两条射线所形成的图形叫做角,故本选项错误;
故选:C.
【点评】本题主要考查了角的概念、射线的概念、直线的性质以及两点间的距离,平面上任意两点间都有一定距离,指的是连接这两点的线段的长度.
10.(3分)按一定规律排列的一列数依次为3,6,12,24,…,按此规律排列下去,这列数的第7个数是( )
A.96 B.124 C.192 D.234
【考点】规律型:数字的变化类.
【专题】规律型;运算能力.
【答案】C
【分析】观察这列数发现每个数是3的倍数,倍数分别是1,2,22,23,…,即可算出第7个数.
【解答】解:观察一系列等式得:第(n+1)个数为3×2n,
则这列数中的7个数为3×26=192.
故选:C.
【点评】此题考查了规律型:数字的变化类,弄清题中的规律是解本题的关键.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)淮北有一天的最低气温是﹣6℃,最高气温是12℃,这一天的最高气温与最低气温相差 18 度.
【考点】有理数的减法;正数和负数.
【专题】计算题;实数;运算能力.
【答案】18.
【分析】根据有理数减法法则计算即可.
【解答】解:由题可知:12﹣(﹣6)=18(℃).
故答案为:18.
【点评】本题考查有理数的减法,掌握有理数减法法则是解题的关键.
12.(3分)若平面内有点A、B、C、D,过其中任意两点画直线,可以画 1或4或6 条直线.
【考点】直线的性质:两点确定一条直线;直线、射线、线段.
【专题】线段、角、相交线与平行线;几何直观.
【答案】1或4或6.
【分析】根据四个点共线,其中三点共线,任意三点不共线3种情况讨论,作出图形可得答案
【解答】解:如图,
故平面内有点A、B、C、D,过其中任意两点画直线,可以画1条或4条或6条直线,
故答案为:1或4或6.
【点评】此题主要考查了直线,关键是掌握两点确定一条直线.
13.(3分)已知,2m﹣5n=﹣5,则代数式4m﹣10n的值为 ﹣10 .
【考点】代数式求值.
【专题】整式;运算能力.
【答案】﹣10.
【分析】代数式4m﹣10n可化成2(2m﹣5n),将2m﹣5n=﹣5代入即可得解.
【解答】解:∵2m﹣5n=﹣5,
∴4m﹣10n=2(2m﹣5n)=2×(﹣5)=﹣10.
故答案为:﹣10.
【点评】此题考查了代数式的求值,解题的关键是整体代入.
14.(3分)钟表上显示10时36分,则此刻时针与分针的夹角的度数为 102 °.
【考点】钟面角.
【专题】线段、角、相交线与平行线;运算能力;推理能力.
【答案】102.
【分析】因为钟表上的刻度是把一个圆平均分成了 12 等份,每一份是30°,借助图形,找出时针和分针之间相差的大格数,用大格数乘 30°即可.
【解答】解:“时针在钟面上每分钟转 0.5°,分针每分钟转6°,
∴钟表上10时36分钟时,时针与分针的夹角可以看成时针转过10时0.5°×36=18°,分针在数字7与8之间.
∵钟表 12 个数字,每相邻两个数字之间的夹角为30°,
∴12时20分钟时分针与时针的夹角2×30°+18°102°.
故答案为:102.
【点评】本题考查钟面角,解答本题的关键是明确钟面角的特点,求出相应的角的度数.
15.(3分)将纸条照如图方式折一下,经测量∠ABC为30°,那么∠CBD= 75° .
【考点】角的计算;翻折变换(折叠问题).
【答案】见试题解答内容
【分析】延长AB,则根据折叠的性质可得,∠EBD=∠CBD,据此即可求解.
【解答】解:延长AB.
则∠EBD=∠CBD75°.
故答案为:75°.
【点评】本题考查了折叠的性质,理解∠EBD=∠CBD是解决本题的关键.
16.(3分)一组“数值转换机”按下面的程序计算,如果输入的数是10,那么输出的结果为19,要使输出的结果为13,则输入的最小正整数是 4 .
【考点】代数式求值;有理数的混合运算.
【专题】计算题;整式.
【答案】见试题解答内容
【分析】根据输出的结果确定出x的所有可能值即可.
【解答】解:当2x﹣1=13时,x=7,
当2x﹣1=7时,x=4,
当2x﹣1=4时,x,不是整数;
所以输入的最小正整数为4,
故答案为:4.
【点评】此题考查了代数式求值,弄清程序中的运算过程是解本题的关键.
三.解答题(共9小题,满分72分,每小题8分)
17.(8分)计算:
(1)2﹣18
(2)﹣14﹣2×(﹣3)2÷||
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】见试题解答内容
【分析】(1)原式利用乘法分配律计算即可求出值;
(2)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可求出值.
【解答】解:(1)原式=2﹣9+14﹣6=1;
(2)原式=﹣1﹣18×3=﹣1﹣54=﹣55.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
18.(8分)解方程:2(x+2)+1=7﹣2(x﹣1).
【考点】解一元一次方程.
【专题】计算题;一次方程(组)及应用;运算能力.
【答案】x=1.
【分析】去括号,移项,合并同类项,系数化为1,解一元一次方程即可.
【解答】解:2(x+2)+1=7﹣2(x﹣1),
去括号得:2x+4+1=7﹣2x+2,
移项得:2x+2x=7+2﹣4﹣1,
合并同类项得:4x=4,
系数化为1得:x=1.
【点评】本题考查了解一元一次方程,解题的关键是掌握解一元一次方程的步骤.
19.(6分)(1)已知代数式3a﹣7b的值为﹣3,求代数式2(2a+b﹣1)+5(a﹣4b+1)﹣3b的值.
(2)先化简,再求值:﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2,其中a=2,b.
【考点】整式的加减—化简求值.
【专题】整式;运算能力.
【答案】(1)﹣6;
(2).
【分析】(1)将代数式2(2a+b﹣1)+5(a﹣4b+1)﹣3b进行化简并整理可得3(3a﹣7b)+3,然后代入已知数据计算即可;
(2)将﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2进行化简,然后将a=2,b代入计算即可.
【解答】解:(1)2(2a+b﹣1)+5(a﹣4b+1)﹣3b
=4a+2b﹣2+5a﹣20b+5﹣3b
=9a﹣21b+3
=3(3a﹣7b)+3,
∵3a﹣7b=﹣3,
∴原式=3×(﹣3)+3=﹣6;
(2)﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2
=﹣5ab+2(3ab﹣4ab2ab)﹣5ab2
=﹣5ab+6ab﹣8ab2+ab﹣5ab2
=2ab﹣13ab2,
∵a=2,b,
∴原式=2×213×2×()2
=2
.
【点评】本题主要考查整式的化简求值,整式化简过程中,去括号时应注意判断去括号后是否需要变号.
20.(6分)阅读下面材料,完成任务.
绝对值的几何意义指的是数轴上的点到原点的距离,例如|2|的几何意义是数轴上表示数2的点到原点之间的距离,我们可以理解为|2﹣0|,同理|7﹣3|的几何意义是数轴上表示数7的点与表示数3的点之间的距离.若出现|7+3|,则先对式子进行调整,得|7﹣(﹣3)|,其几何意义为数轴上表示数7的点与表示数﹣3的点之间的距离.
(1)|﹣1+5|的几何意义是数﹣1和数 ﹣5 的距离,故|﹣1+5|= 4 .
(2)|x﹣2|+|x+3|的最小值是 5 .
(3)|x﹣2|+|x﹣1|+|x+3|的最小值是 5 .
【考点】数轴;绝对值.
【专题】实数;运算能力.
【答案】(1)﹣5,4;
(2)5;
(3)3.
【分析】(1)根据两点间的距离公式即可求解;
(2)根据式子|x﹣2|+|x+3|表示数m到2和﹣3的距离之和即可确定最小值;
(3)根据绝对值的几何意义,可得|x﹣2|+|x﹣1|+|x+3|有最小值,当x=﹣1时,|x﹣2|+|x﹣1|+|x+3|的最小值为5.
【解答】解:(1)|﹣1+5|的几何意义是数﹣1和数﹣5的距离,故|﹣1+5|=4.
故答案为:﹣5,4;
(2)式子|x﹣2|+|x+3|表示数m到2和﹣3的距离之和,
∴|x﹣2|+|x+3|的最小值是|2﹣(﹣3)|=5,
故答案为:5;
(3)根据绝对值的几何意义,可得|x﹣2|+|x﹣1|+|x+3|有最小值,
当x=﹣1时,|x﹣2|+|x﹣1|+|x+3|的最小值为5.
故答案为:5.
【点评】本题考查了数轴,绝对值的性质,读懂题目信息,会利用绝对值的几何意义是解决本题的关键.
21.(6分)如图,已知三点A、B、C,请用尺规作图完成.(保留作图痕迹,不要求写作法)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+AC.
【考点】作图—复杂作图;直线、射线、线段.
【专题】作图题;几何直观.
【答案】(1)(2)(3)作图见解析部分.
【分析】根据直线,射线,线段的定义解决问题即可.
【解答】解:(1)如图,直线AB即为所求作.
(2)如图,射线AC即为所求作.
(3)如图,线段CE即为所求作.
【点评】本题考查作图﹣复杂作图,直线,射线,线段的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
22.(9分)甲、乙两家影院为刺激票房收入,五一期间均推出了优惠活动.
甲影院:3人以内(含3人)按原价购票,超出3人时,超出的人员购票打五折;乙影院:购票一律打八折.
若某电影在两家影院的原价都是60元一张票,小明同学一家人去看电影,若他们到甲、乙两家影院购票费用相同,请问他们一家总共多少人?
【考点】一元一次方程的应用.
【专题】销售问题;一次方程(组)及应用;应用意识.
【答案】他们一家总共5人.
【分析】根据等量关系:在两家影院购票费用相同,列出方程计算即可求解.
【解答】解:设他们一家总共x人,由题意有:
60×3+0.5×60(x﹣3)=0.8×60x,
解得x=5.
故他们一家总共5人.
【点评】此题考查了一元一次方程的应用,弄清题意找到等量关系列出方程是解本题的关键.
23.(9分)如图,在直线l上按指定方向依次取点A,B,C,D,且使AB:BC:CD=2:3:4.若AB的中点M与CD的中点N的距离是15cm,求AB的长.
【考点】两点间的距离.
【专题】线段、角、相交线与平行线;运算能力;推理能力.
【答案】5cm.
【分析】根据题意,设AB=2x cm,则BC=3x cm,CD=4x cm,再根据点M、N分别是线段AB,CD的中点可知BM=x cm,CN=2x cm,再由MN=15cm求出x的值,进而可得出结论.
【解答】解:设AB=2x cm,则BC=3x cm,CD=4x cm,
∵M是AB的中点,N是CD的中点,
∴MBAB,CNCD.
∵AB=2x cm,CD=4xcm,
∴MB=xc m,CN=2x cm.
∵MB+BC+CN=15cm,
∴x+3x+2x=15,
∴x=2.5,
∴AB=5cm.
【点评】本题考查两点间的距离,掌握相关知识是解题的关键.
24.(10分)阅读与理解:
定义:如果两个一元一次方程的解之和为1,我们就称这两个方程互为“美好方程”.
例如:方程2x﹣1=3的解为x=2,x+1=0解为x=﹣1,两个方程解之和为1,所以这两个方程互为“美好方程”.
(1)请判断方程4x﹣(x+5)=1与方程﹣2y﹣y=3是否互为“美好方程”;
(2)若关于x的方程与方程3x=x+4是互为“美好方程”,求m的值.
【考点】一元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】(1)方程4x﹣(x+5)=1与方程﹣2y﹣y=3是互为“美好方程”,理由见解析;
(2).
【分析】(1)根据“美好方程”的定义进行判断即可;
(2)先求出两个方程的解分别为:x=﹣2m,x=2,再根据关于x的方程与方程3x=x+4是互为“美好方程”得出﹣2m+2=1解关于m的方程即可.
【解答】解:(1)解方程4x﹣(x+5)=1得:x=2,
解方程﹣2y﹣y=3得:y=﹣1,
∴x+y=2﹣1=1,
∴方程4x﹣(x+5)=1与方程﹣2y﹣y=3是互为“美好方程”.
(2)关于x的方程的解为:x=﹣2m,
方程3x=x+4的解为x=2,
∵关于x的方程与方程3x=x+4是互为“美好方程”,
∴﹣2m+2=1,
解得:.
【点评】本题主要考查了解一元一次方程,解题的关键是熟练掌握解一元一次方程的方法,准确计算.
25.(10分)定义:在同一平面内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.
如图为一量角器的平面示意图,O为量角器的中心.作射线OA,OB,OC,并将其所对应的量角器内圈刻度分别记为a°,b°,m°.
(1)若射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线.
①如图1,a=0,b=80,则m= 40 ;
②当a=40,b=150时,请在图2中作出射线OA,OB,OC,并直接写出m的值;
③根据①②的经验,得m= (a+b) .(用含a,b的代数式表示).
(2)如图3,a=0,b=m=60.将OA,OB,OC按逆时针方向绕点O同时旋转,旋转速度分别为每秒10°,8°,6°,若旋转t秒后得到的射线OA′,OB',OC'第一次成为“共生三线”,求t的值.
【考点】一元一次方程的应用;角平分线的定义;角的计算;列代数式.
【专题】一次方程(组)及应用;线段、角、相交线与平行线;几何直观;运算能力.
【答案】(1)40.
②m=95.
③(a+b).
(2)10.
【分析】(1)①由射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线,即可求出;
②由条件,得∠AOB=150°﹣40°=110°,易知射线OC是∠AOB的平分线,所以∠AOC∠AOB=55°,m=40+55=95;
③根据①②的经验,得m(a+b).
(2)由题意可知,旋转t s后射线OA′,OB′,OC′对应的刻度分别记为(10t)°,(60+8t)°,(60+6t)°,根据OC′是∠A′OB′的平分线,构建方程即可.
【解答】解:(1)①由题意可知,m40,
故答案为:40.
②由条件,得∠AOB=150°﹣40°=110°,
易知射线OC是∠AOB的平分线,
∴∠AOC∠AOB=55°,
∴m=40+55=95.
③根据①②的经验,得m(a+b).
故答案为:(a+b).
(2)由题意可知,旋转t s后射线OA′,OB′,OC′对应的刻度分别记为(10t)°,(60+8t)°,(60+6t)°,
∵OC′是∠A′OB′的平分线,则(60+6t)﹣(60+8t)=10t﹣(60+6t),
解得,t=10.
∴满足题意的t的值为10.
【点评】本题主要考查了一元一次方程的应用,列代数式,角平分线的定义,角的计算,解题的关键是注意分类讨论.
考点卡片
1.正数和负数
1、在以前学过的0以外的数叫做正数,在正数前面加负号“﹣”,叫做负数,一个数前面的“+”“﹣”号叫做它的符号.
2、0既不是正数也不是负数.0是正负数的分界点,正数是大于0的数,负数是小于0的数.
3、用正负数表示两种具有相反意义的量.具有相反意义的量都是互相依存的两个量,它包含两个要素,一是它们的意义相反,二是它们都是数量.
2.数轴
(1)数轴的概念:规定了原点、正方向、单位长度的直线叫做数轴.
数轴的三要素:原点,单位长度,正方向.
(2)数轴上的点:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数.(一般取右方向为正方向,数轴上的点对应任意实数,包括无理数.)
(3)用数轴比较大小:一般来说,当数轴方向朝右时,右边的数总比左边的数大.
3.相反数
(1)相反数的概念:只有符号不同的两个数叫做互为相反数.
(2)相反数的意义:掌握相反数是成对出现的,不能单独存在,从数轴上看,除0外,互为相反数的两个数,它们分别在原点两旁且到原点距离相等.
(3)多重符号的化简:与“+”个数无关,有奇数个“﹣”号结果为负,有偶数个“﹣”号,结果为正.
(4)规律方法总结:求一个数的相反数的方法就是在这个数的前边添加“﹣”,如a的相反数是﹣a,m+n的相反数是﹣(m+n),这时m+n是一个整体,在整体前面添负号时,要用小括号.
4.绝对值
(1)概念:数轴上某个数与原点的距离叫做这个数的绝对值.
①互为相反数的两个数绝对值相等;
②绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数.
③有理数的绝对值都是非负数.
(2)如果用字母a表示有理数,则数a 绝对值要由字母a本身的取值来确定:
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数﹣a;
③当a是零时,a的绝对值是零.
即|a|={a(a>0)0(a=0)﹣a(a<0)
5.有理数的减法
(1)有理数减法法则:减去一个数,等于加上这个数的相反数. 即:a﹣b=a+(﹣b)
(2)方法指引:
①在进行减法运算时,首先弄清减数的符号;
②将有理数转化为加法时,要同时改变两个符号:一是运算符号(减号变加号); 二是减数的性质符号(减数变相反数);
【注意】:在有理数减法运算时,被减数与减数的位置不能随意交换;因为减法没有交换律.
减法法则不能与加法法则类比,0加任何数都不变,0减任何数应依法则进行计算.
6.有理数的乘法
(1)有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
(2)任何数同零相乘,都得0.
(3)多个有理数相乘的法则:①几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.②几个数相乘,有一个因数为0,积就为0.
(4)方法指引:
①运用乘法法则,先确定符号,再把绝对值相乘.
②多个因数相乘,看0因数和积的符号当先,这样做使运算既准确又简单.
7.有理数的乘方
(1)有理数乘方的定义:求n个相同因数积的运算,叫做乘方.
乘方的结果叫做幂,在an中,a叫做底数,n叫做指数.an读作a的n次方.(将an看作是a的n次方的结果时,也可以读作a的n次幂.)
(2)乘方的法则:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
(3)方法指引:
①有理数的乘方运算与有理数的加减乘除运算一样,首先要确定幂的符号,然后再计算幂的绝对值;
②由于乘方运算比乘除运算又高一级,所以有加减乘除和乘方运算,应先算乘方,再做乘除,最后做加减.
8.有理数的混合运算
(1)有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
【规律方法】有理数混合运算的四种运算技巧
1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.
2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.
3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.
4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.
9.科学记数法—表示较大的数
(1)科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是正整数,这种记数法叫做科学记数法.【科学记数法形式:a×10n,其中1≤a<10,n为正整数.】
(2)规律方法总结:
①科学记数法中a的要求和10的指数n的表示规律为关键,由于10的指数比原来的整数位数少1;按此规律,先数一下原数的整数位数,即可求出10的指数n.
②记数法要求是大于10的数可用科学记数法表示,实质上绝对值大于10的负数同样可用此法表示,只是前面多一个负号.
10.列代数式
(1)定义:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
(2)列代数式五点注意:①仔细辨别词义. 列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分. ②分清数量关系.要正确列代数式,只有分清数量之间的关系. ③注意运算顺序.列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.④规范书写格式.列代数时要按要求规范地书写.像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号.注意代数式括号的适当运用. ⑤正确进行代换.列代数式时,有时需将题中的字母代入公式,这就要求正确进行代换.
【规律方法】列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“ ”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
11.代数式求值
(1)代数式的值:用数值代替代数式里的字母,计算后所得的结果叫做代数式的值.
(2)代数式的求值:求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.
题型简单总结以下三种:
①已知条件不化简,所给代数式化简;
②已知条件化简,所给代数式不化简;
③已知条件和所给代数式都要化简.
12.同类项
(1)定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
同类项中所含字母可以看成是数字、单项式、多项式等.
(2)注意事项:
①一是所含字母相同,二是相同字母的指数也相同,两者缺一不可;
②同类项与系数的大小无关;
③同类项与它们所含的字母顺序无关;
④所有常数项都是同类项.
13.规律型:数字的变化类
探究题是近几年中考命题的亮点,尤其是与数列有关的命题更是层出不穷,形式多样,它要求在已有知识的基础上去探究,观察思考发现规律.
(1)探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法,通常将数字与序号建立数量关系或者与前后数字进行简单运算,从而得出通项公式.
(2)利用方程解决问题.当问题中有多个未知数时,可先设出其中一个为x,再利用它们之间的关系,设出其他未知数,然后列方程.
14.整式的加减—化简求值
给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
15.等式的性质
(1)等式的性质
性质1、等式两边加同一个数(或式子)结果仍得等式;
性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
(2)利用等式的性质解方程
利用等式的性质对方程进行变形,使方程的形式向x=a的形式转化.
应用时要注意把握两关:
①怎样变形;
②依据哪一条,变形时只有做到步步有据,才能保证是正确的.
16.一元一次方程的解
定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.
把方程的解代入原方程,等式左右两边相等.
17.解一元一次方程
(1)解一元一次方程的一般步骤:
去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.
(2)解一元一次方程时先观察方程的形式和特点,若有分母一般先去分母;若既有分母又有括号,且括号外的项在乘括号内各项后能消去分母,就先去括号.
(3)在解类似于“ax+bx=c”的方程时,将方程左边,按合并同类项的方法并为一项即(a+b)x=c.使方程逐渐转化为ax=b的最简形式体现化归思想.将ax=b系数化为1时,要准确计算,一弄清求x时,方程两边除以的是a还是b,尤其a为分数时;二要准确判断符号,a、b同号x为正,a、b异号x为负.
18.由实际问题抽象出一元一次方程
审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.
(1)“总量=各部分量的和”是列方程解应用题中一个基本的关系式,在这一类问题中,表示出各部分的量和总量,然后利用它们之间的等量关系列方程.
(2)“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.通过对同一个量从不同的角度用不同的式子表示,进而列出方程.
19.一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价﹣进价,利润率100%);(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度﹣水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
20.直线、射线、线段
(1)直线、射线、线段的表示方法
①直线:用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB.
②射线:是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.
③线段:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).
(2)点与直线的位置关系:①点经过直线,说明点在直线上;②点不经过直线,说明点在直线外.
21.直线的性质:两点确定一条直线
(1)直线公理:经过两点有且只有一条直线.
简称:两点确定一条直线.
(2)经过一点的直线有无数条,过两点就唯一确定,过三点就不一定了.
22.两点间的距离
(1)两点间的距离
连接两点间的线段的长度叫两点间的距离.
(2)平面上任意两点间都有一定距离,它指的是连接这两点的线段的长度,学习此概念时,注意强调最后的两个字“长度”,也就是说,它是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.可以说画线段,但不能说画距离.
23.角的概念
(1)角的定义:有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.
(2)角的表示方法:角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.
(3)平角、周角:角也可以看作是由一条射线绕它的端点旋转而形成的图形,当始边与终边成一条直线时形成平角,当始 边与终边旋转重合时,形成周角.
(4)角的度量:度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
24.钟面角
(1)钟面一周平均分60格,相邻两格刻度之间的时间间隔是1分钟,时针1分钟走格,分针1分钟走1格.钟面上每一格的度数为360°÷12=30°.
(2)计算钟面上时针与分针所成角的度数,一般先从钟面上找出某一时刻分针与时针所处的位置,确定其夹角,再根据表面上每一格30°的规律,计算出分针与时针的夹角的度数.
(3)钟面上的路程问题
分针:60分钟转一圈,每分钟转动的角度为:360°÷60=6°
时针:12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.
25.方向角
方向角是从正北或正南方向到目标方向所形成的小于90°的角
(1)方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
(2)用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
(3)画方向角
以正南或正北方向作方向角的始边,另一边则表示对象所处的方向的射线.
26.角平分线的定义
(1)角平分线的定义
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
(2)性质:若OC是∠AOB的平分线
则∠AOC=∠BOC∠AOB或∠AOB=2∠AOC=2∠BOC.
(3)平分角的方法有很多,如度量法、折叠法、尺规作图法等,要注意积累,多动手实践.
27.角的计算
(1)角的和差倍分
①∠AOB是∠AOC和∠BOC的和,记作:∠AOB=∠AOC+∠BOC.∠AOC是∠AOB和∠BOC的差,记作:∠AOC=∠AOB﹣∠BOC.②若射线OC是∠AOB的三等分线,则∠AOB=3∠BOC或∠BOC∠AOB.
(2)度、分、秒的加减运算.在进行度分秒的加减时,要将度与度,分与分,秒与秒相加减,分秒相加,逢60要进位,相减时,要借1化60.
(3)度、分、秒的乘除运算.①乘法:度、分、秒分别相乘,结果逢60要进位.②除法:度、分、秒分别去除,把每一次的余数化作下一级单位进一步去除.
28.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
29.垂线
(1)垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
30.作图—复杂作图
复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.
解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
31.翻折变换(折叠问题)
1、翻折变换(折叠问题)实质上就是轴对称变换.
2、折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
3、在解决实际问题时,对于折叠较为复杂的问题可以实际操作图形的折叠,这样便于找到图形间的关系.
首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.我们运用方程解决时,应认真审题,设出正确的未知数.
2024—2025学年上学期长沙初中数学七年级开学模拟试卷1
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下面的数中,与2022的和为0的是( )
A.2022 B.﹣2022 C. D.
2.(3分)2022年宁波舟山港完成货物吞吐量超12.5亿吨,连续14年位居全球第一.其中12.5亿用科学记数法表示为( )
A.12.5×108 B.1.25×109 C.0.125×109 D.1.25×108
3.(3分)下列各组数中,数值相等的是( )
A.﹣35与(﹣5)3 B.﹣35与(﹣3)5
C.﹣34与(﹣5)4 D.(﹣3×5)3与﹣3×53
4.(3分)下列各式中,与3x2y3是同类项的是( )
A.2x5 B.3x3y2 C.x2y3 D.y5
5.(3分)下列等式变形正确的是( )
A.若a=b,则a﹣3=3﹣b B.若ax=ay,则x=y
C.若a=b,则 D.若,则b=d
6.(3分)如图,OC⊥AB于点O,∠1=∠2,则图中互余的角有( )
A.1对 B.2对 C.3对 D.4对
7.(3分)某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
8.(3分)小红所在城市的居民用水实行“阶梯价格”收费,收费办法是:每户用水不超过20m3,每立方米水费x元;超过20m3,每立方米加收1.05元,小红家今年3月份用水28m3,缴纳水费89.6元,根据题意列出关于x的方程,正确的是( )
A.20x+8(x+1.05)=89.6
B.20x+8(x﹣1.05)=89.6
C.28(x+1.05)=89.6
D.28(x+1.05)﹣8×1.05=89.6
9.(3分)下列说法正确的是( )
A.连接两点的线段,叫做两点间的距离
B.射线OA与射线AO表示的是同一条射线
C.经过两点有一条直线,并且只有一条直线
D.从一点引出的两条直线所形成的图形叫做角
10.(3分)按一定规律排列的一列数依次为3,6,12,24,…,按此规律排列下去,这列数的第7个数是( )
A.96 B.124 C.192 D.234
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)淮北有一天的最低气温是﹣6℃,最高气温是12℃,这一天的最高气温与最低气温相差 度.
12.(3分)若平面内有点A、B、C、D,过其中任意两点画直线,可以画 条直线.
13.(3分)已知,2m﹣5n=﹣5,则代数式4m﹣10n的值为 .
14.(3分)钟表上显示10时36分,则此刻时针与分针的夹角的度数为 °.
15.(3分)将纸条照如图方式折一下,经测量∠ABC为30°,那么∠CBD= .
16.(3分)一组“数值转换机”按下面的程序计算,如果输入的数是10,那么输出的结果为19,要使输出的结果为13,则输入的最小正整数是 .
三.解答题(共9小题,满分72分,每小题8分)
17.(8分)计算:
(1)2﹣18
(2)﹣14﹣2×(﹣3)2÷||
18.(8分)解方程:2(x+2)+1=7﹣2(x﹣1).
19.(6分)(1)已知代数式3a﹣7b的值为﹣3,求代数式2(2a+b﹣1)+5(a﹣4b+1)﹣3b的值.
(2)先化简,再求值:﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2,其中a=2,b.
20.(6分)阅读下面材料,完成任务.
绝对值的几何意义指的是数轴上的点到原点的距离,例如|2|的几何意义是数轴上表示数2的点到原点之间的距离,我们可以理解为|2﹣0|,同理|7﹣3|的几何意义是数轴上表示数7的点与表示数3的点之间的距离.若出现|7+3|,则先对式子进行调整,得|7﹣(﹣3)|,其几何意义为数轴上表示数7的点与表示数﹣3的点之间的距离.
(1)|﹣1+5|的几何意义是数﹣1和数 的距离,故|﹣1+5|= .
(2)|x﹣2|+|x+3|的最小值是 .
(3)|x﹣2|+|x﹣1|+|x+3|的最小值是 .
21.(6分)如图,已知三点A、B、C,请用尺规作图完成.(保留作图痕迹,不要求写作法)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+AC.
22.(9分)甲、乙两家影院为刺激票房收入,五一期间均推出了优惠活动.
甲影院:3人以内(含3人)按原价购票,超出3人时,超出的人员购票打五折;乙影院:购票一律打八折.
若某电影在两家影院的原价都是60元一张票,小明同学一家人去看电影,若他们到甲、乙两家影院购票费用相同,请问他们一家总共多少人?
23.(9分)如图,在直线l上按指定方向依次取点A,B,C,D,且使AB:BC:CD=2:3:4.若AB的中点M与CD的中点N的距离是15cm,求AB的长.
24.(10分)阅读与理解:
定义:如果两个一元一次方程的解之和为1,我们就称这两个方程互为“美好方程”.
例如:方程2x﹣1=3的解为x=2,x+1=0解为x=﹣1,两个方程解之和为1,所以这两个方程互为“美好方程”.
(1)请判断方程4x﹣(x+5)=1与方程﹣2y﹣y=3是否互为“美好方程”;
(2)若关于x的方程与方程3x=x+4是互为“美好方程”,求m的值.
25.(10分)定义:在同一平面内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.
如图为一量角器的平面示意图,O为量角器的中心.作射线OA,OB,OC,并将其所对应的量角器内圈刻度分别记为a°,b°,m°.
(1)若射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线.
①如图1,a=0,b=80,则m= ;
②当a=40,b=150时,请在图2中作出射线OA,OB,OC,并直接写出m的值;
③根据①②的经验,得m= .(用含a,b的代数式表示).
(2)如图3,a=0,b=m=60.将OA,OB,OC按逆时针方向绕点O同时旋转,旋转速度分别为每秒10°,8°,6°,若旋转t秒后得到的射线OA′,OB',OC'第一次成为“共生三线”,求t的值.
2024—2025学年上学期长沙初中数学七年级开学模拟试卷1
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下面的数中,与2022的和为0的是( )
A.2022 B.﹣2022 C. D.
【考点】相反数.
【专题】计算题;实数;运算能力.
【答案】B
【分析】利用有理数的加法或互为相反数的定义计算并判断.
【解答】解:与2022的和为0的数是﹣2022,
故选:B.
【点评】本题考查了有理数的加法法则,解题的关键是掌握有理数的加法法则.
2.(3分)2022年宁波舟山港完成货物吞吐量超12.5亿吨,连续14年位居全球第一.其中12.5亿用科学记数法表示为( )
A.12.5×108 B.1.25×109 C.0.125×109 D.1.25×108
【考点】科学记数法—表示较大的数.
【专题】实数;数感.
【答案】B
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
【解答】解:12.5亿=1250000000=1.25×109.
故选:B.
【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
3.(3分)下列各组数中,数值相等的是( )
A.﹣35与(﹣5)3 B.﹣35与(﹣3)5
C.﹣34与(﹣5)4 D.(﹣3×5)3与﹣3×53
【考点】有理数的乘方;有理数的乘法.
【专题】实数;运算能力.
【答案】B
【分析】根据有理数的乘方、有理数的乘法法则解决此题.
【解答】解:A.根据有理数的乘方,﹣35=﹣243,(﹣5)3=﹣125,故﹣35≠(﹣5)3,那么A不符合题意.
B.根据有理数的乘方,﹣35=﹣243,(﹣3)5=﹣243,故﹣35=(﹣3)5,那么B符合题意.
C.根据有理数的乘方,﹣34=﹣81,(﹣5)4=625,那么﹣34≠(﹣5)4,那么C不符合题意.
D.根据有理数的乘法以及乘方,(﹣3×5)3=﹣27×53≠﹣3×53,那么D不符合题意.
故选:B.
【点评】本题主要考查有理数的乘方、有理数的乘法,熟练掌握有理数的乘方、有理数的乘法法则是解决本题的关键.
4.(3分)下列各式中,与3x2y3是同类项的是( )
A.2x5 B.3x3y2 C.x2y3 D.y5
【考点】同类项.
【专题】整式;数感;符号意识;模型思想.
【答案】C
【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,进行判断即可.
【解答】解:A、2x5与3x2y3不是同类项,故本选项错误;
B、3x3y2与3x2y3不是同类项,故本选项错误;
C、x2y3与3x2y3是同类项,故本选项正确;
D、y5与3x2y3不是同类项,故本选项错误;
故选:C.
【点评】本题考查了同类项的知识,解答本题的关键是理解同类项的定义.
5.(3分)下列等式变形正确的是( )
A.若a=b,则a﹣3=3﹣b B.若ax=ay,则x=y
C.若a=b,则 D.若,则b=d
【考点】等式的性质.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】根据等式的性质逐个判断即可.
【解答】解:A.∵a=b,
∴a﹣3=b﹣3,故本选项不符合题意;
B.当a=0时,由ax=ay不能推出x=y,故本选项不符合题意;
C.当c=0时,由a=b不能推出,故本选项不符合题意;
D.∵,
∴等式两边都乘c得:b=d,故本选项符合题意;
故选:D.
【点评】本题考查了等式的性质,能熟记等式的性质是解此题的关键,等式的性质1:等式的两边加(或减)同一个数(或式子),等式仍成立;等式的性质2:等式的两边乘同一个数,等式仍成立;等式的两边都除以同一个不等于0的数,等式仍成立.
6.(3分)如图,OC⊥AB于点O,∠1=∠2,则图中互余的角有( )
A.1对 B.2对 C.3对 D.4对
【考点】垂线;余角和补角.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】D
【分析】根据OC⊥AB于点O,可知∠1与∠AOD互为余角,∠2与∠COD互为余角,又因为∠1=∠2,则相互交换又多了两对互余角.
【解答】解:∵OC⊥AB,
∴∠1+∠AOD=90°,∠2+∠COE=90°,
即∠1与∠AOD互为余角,∠2与∠COE互为余角,
∵∠1=∠2,
∴∠1+∠COE=90°,∠2+∠AOD=90°,
即∠1与∠COE互为余角,∠2与∠AOD互为余角.
所以图中互余的角有4对.
故选:D.
【点评】本题考查了垂线的知识,解答本题的关键是根据垂直得出直角,继而找到互余的角.
7.(3分)某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
【考点】方向角.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】B
【分析】根据方位角的概念画出图形,再根据已知结合角的和差关系求解.
【解答】解:如图所示:
∵某人在A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,
∴∠BAD=40°,∠CAD=35°,
∴∠BAC=∠BAD+∠CAD=40°+35°=75°.
故选:B.
【点评】本题考查了方向角,解答此类题关键是需要从运动的角度,正确画出方位角,再结合角的和差关系求解.
8.(3分)小红所在城市的居民用水实行“阶梯价格”收费,收费办法是:每户用水不超过20m3,每立方米水费x元;超过20m3,每立方米加收1.05元,小红家今年3月份用水28m3,缴纳水费89.6元,根据题意列出关于x的方程,正确的是( )
A.20x+8(x+1.05)=89.6
B.20x+8(x﹣1.05)=89.6
C.28(x+1.05)=89.6
D.28(x+1.05)﹣8×1.05=89.6
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;应用意识.
【答案】A
【分析】利用总价=单价×数量,结合“阶梯价格”收费标准,即可得出关于x的一元一次方程,此题得解.
【解答】解:根据题意得:20x+(28﹣20)(x+1.05)=89.6,
即20x+8(x+1.05)=89.6.
故选:A.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
9.(3分)下列说法正确的是( )
A.连接两点的线段,叫做两点间的距离
B.射线OA与射线AO表示的是同一条射线
C.经过两点有一条直线,并且只有一条直线
D.从一点引出的两条直线所形成的图形叫做角
【考点】角的概念;直线、射线、线段;直线的性质:两点确定一条直线;两点间的距离.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】依据角的概念、射线的概念、直线的性质以及两点间的距离,即可得到正确结论.
【解答】解:A.连接两点的线段的长度,叫做两点间的距离,故本选项错误;
B.射线OA与射线AO表示的是不同的两条射线,故本选项错误;
C.经过两点有一条直线,并且只有一条直线,故本选项正确;
D.从一点引出的两条射线所形成的图形叫做角,故本选项错误;
故选:C.
【点评】本题主要考查了角的概念、射线的概念、直线的性质以及两点间的距离,平面上任意两点间都有一定距离,指的是连接这两点的线段的长度.
10.(3分)按一定规律排列的一列数依次为3,6,12,24,…,按此规律排列下去,这列数的第7个数是( )
A.96 B.124 C.192 D.234
【考点】规律型:数字的变化类.
【专题】规律型;运算能力.
【答案】C
【分析】观察这列数发现每个数是3的倍数,倍数分别是1,2,22,23,…,即可算出第7个数.
【解答】解:观察一系列等式得:第(n+1)个数为3×2n,
则这列数中的7个数为3×26=192.
故选:C.
【点评】此题考查了规律型:数字的变化类,弄清题中的规律是解本题的关键.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)淮北有一天的最低气温是﹣6℃,最高气温是12℃,这一天的最高气温与最低气温相差 18 度.
【考点】有理数的减法;正数和负数.
【专题】计算题;实数;运算能力.
【答案】18.
【分析】根据有理数减法法则计算即可.
【解答】解:由题可知:12﹣(﹣6)=18(℃).
故答案为:18.
【点评】本题考查有理数的减法,掌握有理数减法法则是解题的关键.
12.(3分)若平面内有点A、B、C、D,过其中任意两点画直线,可以画 1或4或6 条直线.
【考点】直线的性质:两点确定一条直线;直线、射线、线段.
【专题】线段、角、相交线与平行线;几何直观.
【答案】1或4或6.
【分析】根据四个点共线,其中三点共线,任意三点不共线3种情况讨论,作出图形可得答案
【解答】解:如图,
故平面内有点A、B、C、D,过其中任意两点画直线,可以画1条或4条或6条直线,
故答案为:1或4或6.
【点评】此题主要考查了直线,关键是掌握两点确定一条直线.
13.(3分)已知,2m﹣5n=﹣5,则代数式4m﹣10n的值为 ﹣10 .
【考点】代数式求值.
【专题】整式;运算能力.
【答案】﹣10.
【分析】代数式4m﹣10n可化成2(2m﹣5n),将2m﹣5n=﹣5代入即可得解.
【解答】解:∵2m﹣5n=﹣5,
∴4m﹣10n=2(2m﹣5n)=2×(﹣5)=﹣10.
故答案为:﹣10.
【点评】此题考查了代数式的求值,解题的关键是整体代入.
14.(3分)钟表上显示10时36分,则此刻时针与分针的夹角的度数为 102 °.
【考点】钟面角.
【专题】线段、角、相交线与平行线;运算能力;推理能力.
【答案】102.
【分析】因为钟表上的刻度是把一个圆平均分成了 12 等份,每一份是30°,借助图形,找出时针和分针之间相差的大格数,用大格数乘 30°即可.
【解答】解:“时针在钟面上每分钟转 0.5°,分针每分钟转6°,
∴钟表上10时36分钟时,时针与分针的夹角可以看成时针转过10时0.5°×36=18°,分针在数字7与8之间.
∵钟表 12 个数字,每相邻两个数字之间的夹角为30°,
∴12时20分钟时分针与时针的夹角2×30°+18°102°.
故答案为:102.
【点评】本题考查钟面角,解答本题的关键是明确钟面角的特点,求出相应的角的度数.
15.(3分)将纸条照如图方式折一下,经测量∠ABC为30°,那么∠CBD= 75° .
【考点】角的计算;翻折变换(折叠问题).
【答案】见试题解答内容
【分析】延长AB,则根据折叠的性质可得,∠EBD=∠CBD,据此即可求解.
【解答】解:延长AB.
则∠EBD=∠CBD75°.
故答案为:75°.
【点评】本题考查了折叠的性质,理解∠EBD=∠CBD是解决本题的关键.
16.(3分)一组“数值转换机”按下面的程序计算,如果输入的数是10,那么输出的结果为19,要使输出的结果为13,则输入的最小正整数是 4 .
【考点】代数式求值;有理数的混合运算.
【专题】计算题;整式.
【答案】见试题解答内容
【分析】根据输出的结果确定出x的所有可能值即可.
【解答】解:当2x﹣1=13时,x=7,
当2x﹣1=7时,x=4,
当2x﹣1=4时,x,不是整数;
所以输入的最小正整数为4,
故答案为:4.
【点评】此题考查了代数式求值,弄清程序中的运算过程是解本题的关键.
三.解答题(共9小题,满分72分,每小题8分)
17.(8分)计算:
(1)2﹣18
(2)﹣14﹣2×(﹣3)2÷||
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】见试题解答内容
【分析】(1)原式利用乘法分配律计算即可求出值;
(2)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可求出值.
【解答】解:(1)原式=2﹣9+14﹣6=1;
(2)原式=﹣1﹣18×3=﹣1﹣54=﹣55.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
18.(8分)解方程:2(x+2)+1=7﹣2(x﹣1).
【考点】解一元一次方程.
【专题】计算题;一次方程(组)及应用;运算能力.
【答案】x=1.
【分析】去括号,移项,合并同类项,系数化为1,解一元一次方程即可.
【解答】解:2(x+2)+1=7﹣2(x﹣1),
去括号得:2x+4+1=7﹣2x+2,
移项得:2x+2x=7+2﹣4﹣1,
合并同类项得:4x=4,
系数化为1得:x=1.
【点评】本题考查了解一元一次方程,解题的关键是掌握解一元一次方程的步骤.
19.(6分)(1)已知代数式3a﹣7b的值为﹣3,求代数式2(2a+b﹣1)+5(a﹣4b+1)﹣3b的值.
(2)先化简,再求值:﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2,其中a=2,b.
【考点】整式的加减—化简求值.
【专题】整式;运算能力.
【答案】(1)﹣6;
(2).
【分析】(1)将代数式2(2a+b﹣1)+5(a﹣4b+1)﹣3b进行化简并整理可得3(3a﹣7b)+3,然后代入已知数据计算即可;
(2)将﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2进行化简,然后将a=2,b代入计算即可.
【解答】解:(1)2(2a+b﹣1)+5(a﹣4b+1)﹣3b
=4a+2b﹣2+5a﹣20b+5﹣3b
=9a﹣21b+3
=3(3a﹣7b)+3,
∵3a﹣7b=﹣3,
∴原式=3×(﹣3)+3=﹣6;
(2)﹣5ab+2[3ab﹣(4ab2ab)]﹣5ab2
=﹣5ab+2(3ab﹣4ab2ab)﹣5ab2
=﹣5ab+6ab﹣8ab2+ab﹣5ab2
=2ab﹣13ab2,
∵a=2,b,
∴原式=2×213×2×()2
=2
.
【点评】本题主要考查整式的化简求值,整式化简过程中,去括号时应注意判断去括号后是否需要变号.
20.(6分)阅读下面材料,完成任务.
绝对值的几何意义指的是数轴上的点到原点的距离,例如|2|的几何意义是数轴上表示数2的点到原点之间的距离,我们可以理解为|2﹣0|,同理|7﹣3|的几何意义是数轴上表示数7的点与表示数3的点之间的距离.若出现|7+3|,则先对式子进行调整,得|7﹣(﹣3)|,其几何意义为数轴上表示数7的点与表示数﹣3的点之间的距离.
(1)|﹣1+5|的几何意义是数﹣1和数 ﹣5 的距离,故|﹣1+5|= 4 .
(2)|x﹣2|+|x+3|的最小值是 5 .
(3)|x﹣2|+|x﹣1|+|x+3|的最小值是 5 .
【考点】数轴;绝对值.
【专题】实数;运算能力.
【答案】(1)﹣5,4;
(2)5;
(3)3.
【分析】(1)根据两点间的距离公式即可求解;
(2)根据式子|x﹣2|+|x+3|表示数m到2和﹣3的距离之和即可确定最小值;
(3)根据绝对值的几何意义,可得|x﹣2|+|x﹣1|+|x+3|有最小值,当x=﹣1时,|x﹣2|+|x﹣1|+|x+3|的最小值为5.
【解答】解:(1)|﹣1+5|的几何意义是数﹣1和数﹣5的距离,故|﹣1+5|=4.
故答案为:﹣5,4;
(2)式子|x﹣2|+|x+3|表示数m到2和﹣3的距离之和,
∴|x﹣2|+|x+3|的最小值是|2﹣(﹣3)|=5,
故答案为:5;
(3)根据绝对值的几何意义,可得|x﹣2|+|x﹣1|+|x+3|有最小值,
当x=﹣1时,|x﹣2|+|x﹣1|+|x+3|的最小值为5.
故答案为:5.
【点评】本题考查了数轴,绝对值的性质,读懂题目信息,会利用绝对值的几何意义是解决本题的关键.
21.(6分)如图,已知三点A、B、C,请用尺规作图完成.(保留作图痕迹,不要求写作法)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+AC.
【考点】作图—复杂作图;直线、射线、线段.
【专题】作图题;几何直观.
【答案】(1)(2)(3)作图见解析部分.
【分析】根据直线,射线,线段的定义解决问题即可.
【解答】解:(1)如图,直线AB即为所求作.
(2)如图,射线AC即为所求作.
(3)如图,线段CE即为所求作.
【点评】本题考查作图﹣复杂作图,直线,射线,线段的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
22.(9分)甲、乙两家影院为刺激票房收入,五一期间均推出了优惠活动.
甲影院:3人以内(含3人)按原价购票,超出3人时,超出的人员购票打五折;乙影院:购票一律打八折.
若某电影在两家影院的原价都是60元一张票,小明同学一家人去看电影,若他们到甲、乙两家影院购票费用相同,请问他们一家总共多少人?
【考点】一元一次方程的应用.
【专题】销售问题;一次方程(组)及应用;应用意识.
【答案】他们一家总共5人.
【分析】根据等量关系:在两家影院购票费用相同,列出方程计算即可求解.
【解答】解:设他们一家总共x人,由题意有:
60×3+0.5×60(x﹣3)=0.8×60x,
解得x=5.
故他们一家总共5人.
【点评】此题考查了一元一次方程的应用,弄清题意找到等量关系列出方程是解本题的关键.
23.(9分)如图,在直线l上按指定方向依次取点A,B,C,D,且使AB:BC:CD=2:3:4.若AB的中点M与CD的中点N的距离是15cm,求AB的长.
【考点】两点间的距离.
【专题】线段、角、相交线与平行线;运算能力;推理能力.
【答案】5cm.
【分析】根据题意,设AB=2x cm,则BC=3x cm,CD=4x cm,再根据点M、N分别是线段AB,CD的中点可知BM=x cm,CN=2x cm,再由MN=15cm求出x的值,进而可得出结论.
【解答】解:设AB=2x cm,则BC=3x cm,CD=4x cm,
∵M是AB的中点,N是CD的中点,
∴MBAB,CNCD.
∵AB=2x cm,CD=4xcm,
∴MB=xc m,CN=2x cm.
∵MB+BC+CN=15cm,
∴x+3x+2x=15,
∴x=2.5,
∴AB=5cm.
【点评】本题考查两点间的距离,掌握相关知识是解题的关键.
24.(10分)阅读与理解:
定义:如果两个一元一次方程的解之和为1,我们就称这两个方程互为“美好方程”.
例如:方程2x﹣1=3的解为x=2,x+1=0解为x=﹣1,两个方程解之和为1,所以这两个方程互为“美好方程”.
(1)请判断方程4x﹣(x+5)=1与方程﹣2y﹣y=3是否互为“美好方程”;
(2)若关于x的方程与方程3x=x+4是互为“美好方程”,求m的值.
【考点】一元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】(1)方程4x﹣(x+5)=1与方程﹣2y﹣y=3是互为“美好方程”,理由见解析;
(2).
【分析】(1)根据“美好方程”的定义进行判断即可;
(2)先求出两个方程的解分别为:x=﹣2m,x=2,再根据关于x的方程与方程3x=x+4是互为“美好方程”得出﹣2m+2=1解关于m的方程即可.
【解答】解:(1)解方程4x﹣(x+5)=1得:x=2,
解方程﹣2y﹣y=3得:y=﹣1,
∴x+y=2﹣1=1,
∴方程4x﹣(x+5)=1与方程﹣2y﹣y=3是互为“美好方程”.
(2)关于x的方程的解为:x=﹣2m,
方程3x=x+4的解为x=2,
∵关于x的方程与方程3x=x+4是互为“美好方程”,
∴﹣2m+2=1,
解得:.
【点评】本题主要考查了解一元一次方程,解题的关键是熟练掌握解一元一次方程的方法,准确计算.
25.(10分)定义:在同一平面内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.
如图为一量角器的平面示意图,O为量角器的中心.作射线OA,OB,OC,并将其所对应的量角器内圈刻度分别记为a°,b°,m°.
(1)若射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线.
①如图1,a=0,b=80,则m= 40 ;
②当a=40,b=150时,请在图2中作出射线OA,OB,OC,并直接写出m的值;
③根据①②的经验,得m= (a+b) .(用含a,b的代数式表示).
(2)如图3,a=0,b=m=60.将OA,OB,OC按逆时针方向绕点O同时旋转,旋转速度分别为每秒10°,8°,6°,若旋转t秒后得到的射线OA′,OB',OC'第一次成为“共生三线”,求t的值.
【考点】一元一次方程的应用;角平分线的定义;角的计算;列代数式.
【专题】一次方程(组)及应用;线段、角、相交线与平行线;几何直观;运算能力.
【答案】(1)40.
②m=95.
③(a+b).
(2)10.
【分析】(1)①由射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线,即可求出;
②由条件,得∠AOB=150°﹣40°=110°,易知射线OC是∠AOB的平分线,所以∠AOC∠AOB=55°,m=40+55=95;
③根据①②的经验,得m(a+b).
(2)由题意可知,旋转t s后射线OA′,OB′,OC′对应的刻度分别记为(10t)°,(60+8t)°,(60+6t)°,根据OC′是∠A′OB′的平分线,构建方程即可.
【解答】解:(1)①由题意可知,m40,
故答案为:40.
②由条件,得∠AOB=150°﹣40°=110°,
易知射线OC是∠AOB的平分线,
∴∠AOC∠AOB=55°,
∴m=40+55=95.
③根据①②的经验,得m(a+b).
故答案为:(a+b).
(2)由题意可知,旋转t s后射线OA′,OB′,OC′对应的刻度分别记为(10t)°,(60+8t)°,(60+6t)°,
∵OC′是∠A′OB′的平分线,则(60+6t)﹣(60+8t)=10t﹣(60+6t),
解得,t=10.
∴满足题意的t的值为10.
【点评】本题主要考查了一元一次方程的应用,列代数式,角平分线的定义,角的计算,解题的关键是注意分类讨论.
考点卡片
1.正数和负数
1、在以前学过的0以外的数叫做正数,在正数前面加负号“﹣”,叫做负数,一个数前面的“+”“﹣”号叫做它的符号.
2、0既不是正数也不是负数.0是正负数的分界点,正数是大于0的数,负数是小于0的数.
3、用正负数表示两种具有相反意义的量.具有相反意义的量都是互相依存的两个量,它包含两个要素,一是它们的意义相反,二是它们都是数量.
2.数轴
(1)数轴的概念:规定了原点、正方向、单位长度的直线叫做数轴.
数轴的三要素:原点,单位长度,正方向.
(2)数轴上的点:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数.(一般取右方向为正方向,数轴上的点对应任意实数,包括无理数.)
(3)用数轴比较大小:一般来说,当数轴方向朝右时,右边的数总比左边的数大.
3.相反数
(1)相反数的概念:只有符号不同的两个数叫做互为相反数.
(2)相反数的意义:掌握相反数是成对出现的,不能单独存在,从数轴上看,除0外,互为相反数的两个数,它们分别在原点两旁且到原点距离相等.
(3)多重符号的化简:与“+”个数无关,有奇数个“﹣”号结果为负,有偶数个“﹣”号,结果为正.
(4)规律方法总结:求一个数的相反数的方法就是在这个数的前边添加“﹣”,如a的相反数是﹣a,m+n的相反数是﹣(m+n),这时m+n是一个整体,在整体前面添负号时,要用小括号.
4.绝对值
(1)概念:数轴上某个数与原点的距离叫做这个数的绝对值.
①互为相反数的两个数绝对值相等;
②绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数.
③有理数的绝对值都是非负数.
(2)如果用字母a表示有理数,则数a 绝对值要由字母a本身的取值来确定:
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数﹣a;
③当a是零时,a的绝对值是零.
即|a|={a(a>0)0(a=0)﹣a(a<0)
5.有理数的减法
(1)有理数减法法则:减去一个数,等于加上这个数的相反数. 即:a﹣b=a+(﹣b)
(2)方法指引:
①在进行减法运算时,首先弄清减数的符号;
②将有理数转化为加法时,要同时改变两个符号:一是运算符号(减号变加号); 二是减数的性质符号(减数变相反数);
【注意】:在有理数减法运算时,被减数与减数的位置不能随意交换;因为减法没有交换律.
减法法则不能与加法法则类比,0加任何数都不变,0减任何数应依法则进行计算.
6.有理数的乘法
(1)有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
(2)任何数同零相乘,都得0.
(3)多个有理数相乘的法则:①几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.②几个数相乘,有一个因数为0,积就为0.
(4)方法指引:
①运用乘法法则,先确定符号,再把绝对值相乘.
②多个因数相乘,看0因数和积的符号当先,这样做使运算既准确又简单.
7.有理数的乘方
(1)有理数乘方的定义:求n个相同因数积的运算,叫做乘方.
乘方的结果叫做幂,在an中,a叫做底数,n叫做指数.an读作a的n次方.(将an看作是a的n次方的结果时,也可以读作a的n次幂.)
(2)乘方的法则:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
(3)方法指引:
①有理数的乘方运算与有理数的加减乘除运算一样,首先要确定幂的符号,然后再计算幂的绝对值;
②由于乘方运算比乘除运算又高一级,所以有加减乘除和乘方运算,应先算乘方,再做乘除,最后做加减.
8.有理数的混合运算
(1)有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
【规律方法】有理数混合运算的四种运算技巧
1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.
2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.
3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.
4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.
9.科学记数法—表示较大的数
(1)科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是正整数,这种记数法叫做科学记数法.【科学记数法形式:a×10n,其中1≤a<10,n为正整数.】
(2)规律方法总结:
①科学记数法中a的要求和10的指数n的表示规律为关键,由于10的指数比原来的整数位数少1;按此规律,先数一下原数的整数位数,即可求出10的指数n.
②记数法要求是大于10的数可用科学记数法表示,实质上绝对值大于10的负数同样可用此法表示,只是前面多一个负号.
10.列代数式
(1)定义:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
(2)列代数式五点注意:①仔细辨别词义. 列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分. ②分清数量关系.要正确列代数式,只有分清数量之间的关系. ③注意运算顺序.列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.④规范书写格式.列代数时要按要求规范地书写.像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号.注意代数式括号的适当运用. ⑤正确进行代换.列代数式时,有时需将题中的字母代入公式,这就要求正确进行代换.
【规律方法】列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“ ”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
11.代数式求值
(1)代数式的值:用数值代替代数式里的字母,计算后所得的结果叫做代数式的值.
(2)代数式的求值:求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.
题型简单总结以下三种:
①已知条件不化简,所给代数式化简;
②已知条件化简,所给代数式不化简;
③已知条件和所给代数式都要化简.
12.同类项
(1)定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
同类项中所含字母可以看成是数字、单项式、多项式等.
(2)注意事项:
①一是所含字母相同,二是相同字母的指数也相同,两者缺一不可;
②同类项与系数的大小无关;
③同类项与它们所含的字母顺序无关;
④所有常数项都是同类项.
13.规律型:数字的变化类
探究题是近几年中考命题的亮点,尤其是与数列有关的命题更是层出不穷,形式多样,它要求在已有知识的基础上去探究,观察思考发现规律.
(1)探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法,通常将数字与序号建立数量关系或者与前后数字进行简单运算,从而得出通项公式.
(2)利用方程解决问题.当问题中有多个未知数时,可先设出其中一个为x,再利用它们之间的关系,设出其他未知数,然后列方程.
14.整式的加减—化简求值
给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
15.等式的性质
(1)等式的性质
性质1、等式两边加同一个数(或式子)结果仍得等式;
性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
(2)利用等式的性质解方程
利用等式的性质对方程进行变形,使方程的形式向x=a的形式转化.
应用时要注意把握两关:
①怎样变形;
②依据哪一条,变形时只有做到步步有据,才能保证是正确的.
16.一元一次方程的解
定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.
把方程的解代入原方程,等式左右两边相等.
17.解一元一次方程
(1)解一元一次方程的一般步骤:
去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.
(2)解一元一次方程时先观察方程的形式和特点,若有分母一般先去分母;若既有分母又有括号,且括号外的项在乘括号内各项后能消去分母,就先去括号.
(3)在解类似于“ax+bx=c”的方程时,将方程左边,按合并同类项的方法并为一项即(a+b)x=c.使方程逐渐转化为ax=b的最简形式体现化归思想.将ax=b系数化为1时,要准确计算,一弄清求x时,方程两边除以的是a还是b,尤其a为分数时;二要准确判断符号,a、b同号x为正,a、b异号x为负.
18.由实际问题抽象出一元一次方程
审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.
(1)“总量=各部分量的和”是列方程解应用题中一个基本的关系式,在这一类问题中,表示出各部分的量和总量,然后利用它们之间的等量关系列方程.
(2)“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.通过对同一个量从不同的角度用不同的式子表示,进而列出方程.
19.一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价﹣进价,利润率100%);(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度﹣水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
20.直线、射线、线段
(1)直线、射线、线段的表示方法
①直线:用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB.
②射线:是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.
③线段:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).
(2)点与直线的位置关系:①点经过直线,说明点在直线上;②点不经过直线,说明点在直线外.
21.直线的性质:两点确定一条直线
(1)直线公理:经过两点有且只有一条直线.
简称:两点确定一条直线.
(2)经过一点的直线有无数条,过两点就唯一确定,过三点就不一定了.
22.两点间的距离
(1)两点间的距离
连接两点间的线段的长度叫两点间的距离.
(2)平面上任意两点间都有一定距离,它指的是连接这两点的线段的长度,学习此概念时,注意强调最后的两个字“长度”,也就是说,它是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.可以说画线段,但不能说画距离.
23.角的概念
(1)角的定义:有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.
(2)角的表示方法:角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.
(3)平角、周角:角也可以看作是由一条射线绕它的端点旋转而形成的图形,当始边与终边成一条直线时形成平角,当始 边与终边旋转重合时,形成周角.
(4)角的度量:度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
24.钟面角
(1)钟面一周平均分60格,相邻两格刻度之间的时间间隔是1分钟,时针1分钟走格,分针1分钟走1格.钟面上每一格的度数为360°÷12=30°.
(2)计算钟面上时针与分针所成角的度数,一般先从钟面上找出某一时刻分针与时针所处的位置,确定其夹角,再根据表面上每一格30°的规律,计算出分针与时针的夹角的度数.
(3)钟面上的路程问题
分针:60分钟转一圈,每分钟转动的角度为:360°÷60=6°
时针:12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.
25.方向角
方向角是从正北或正南方向到目标方向所形成的小于90°的角
(1)方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
(2)用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
(3)画方向角
以正南或正北方向作方向角的始边,另一边则表示对象所处的方向的射线.
26.角平分线的定义
(1)角平分线的定义
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
(2)性质:若OC是∠AOB的平分线
则∠AOC=∠BOC∠AOB或∠AOB=2∠AOC=2∠BOC.
(3)平分角的方法有很多,如度量法、折叠法、尺规作图法等,要注意积累,多动手实践.
27.角的计算
(1)角的和差倍分
①∠AOB是∠AOC和∠BOC的和,记作:∠AOB=∠AOC+∠BOC.∠AOC是∠AOB和∠BOC的差,记作:∠AOC=∠AOB﹣∠BOC.②若射线OC是∠AOB的三等分线,则∠AOB=3∠BOC或∠BOC∠AOB.
(2)度、分、秒的加减运算.在进行度分秒的加减时,要将度与度,分与分,秒与秒相加减,分秒相加,逢60要进位,相减时,要借1化60.
(3)度、分、秒的乘除运算.①乘法:度、分、秒分别相乘,结果逢60要进位.②除法:度、分、秒分别去除,把每一次的余数化作下一级单位进一步去除.
28.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
29.垂线
(1)垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
30.作图—复杂作图
复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.
解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
31.翻折变换(折叠问题)
1、翻折变换(折叠问题)实质上就是轴对称变换.
2、折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
3、在解决实际问题时,对于折叠较为复杂的问题可以实际操作图形的折叠,这样便于找到图形间的关系.
首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.我们运用方程解决时,应认真审题,设出正确的未知数.
同课章节目录
