湖北省武汉市新洲区部分学校2023-2024学年高二下学期6月期末质量检测数学试卷(含解析)
文档属性
| 名称 | 湖北省武汉市新洲区部分学校2023-2024学年高二下学期6月期末质量检测数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 885.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 20:32:33 | ||
图片预览




文档简介
湖北省武汉市新洲区部分学校2023-2024学年高二下学期6月期末质量检测数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.设等差数列满足,,则( )
A.80 B.100 C.120 D.160
2.若圆与圆的公共弦长为则( )
A. B. C.2 D.4
3.的展开式中含项的系数为( )
A. B. C.28 D.56
4.5G技术在我国已经进入调整发展的阶段,5G手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:
时间x 1 2 3 4 5
销售量y(千只) 0.5 0.8 1.0 1.2 1.5
若x与y线性相关,且线性回归方程为,则下列说法正确的是( )
A.由题中数据可知,变量y与x正相关,且相关系数
B.当解释变量x每增加1个单位时,预报变量9平均增加个单位
C.线性回归方程中
D.可以预测时,该商场5G手机销量约为1.72(千只)
5.2024年“与辉同行”直播间开播,董宇辉领衔7位主播从“心”出发,其中男性5人,女性3人,现需排班晚8:00黄金档,随机抽取两人,则女生人数的期望为( )
A. B. C. D.
6.甲辰龙年春节哈尔滨火爆出圈,成为春节假期旅游城市中的“顶流”.甲,乙等6名网红主播在哈尔滨的中央大街,冰雪大世界,圣索菲亚教堂,音乐长廊4个景点中选择一个打卡游玩,若每个景点至少有一个主播去打卡游玩,每位主播都会选择一个景点打卡游玩,且甲,乙各单独1人去某一个景点打卡游玩,则不同游玩方法有( )
A.96种 B.132种 C.168种 D.204种
7.质数(primenumber)又称素数,一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则这个数为质数.数学上把相差为2的两个素数叫做“孪生素数”,如:3和5,5和7,…,那么,如果我们在不超过30的自然数中,随机选取两个不同的数,记事件A:这两个数都是素数:事件B:这两个数不是孪生素数,则( )
A. B. C. D.
8.已知函数,,若对任意的,,都有成立,则实数a的取值范围是( )
A. B. C.D.
二、多项选择题
9.对于的展开式中,只有第5项的二项式系数最大,则下列说法正确的是( )
A. B.展开式的各项系数之和为l
C.展开式的二项式系数之和为512 D.展开式中的含项系数是1792
10.定义在上的函数满足,,(若则,c为常数),则下列说法正确的是( )
A.在.处取得极大值,极大值为
B.恰有两个零点
C.若在上恒成立,则
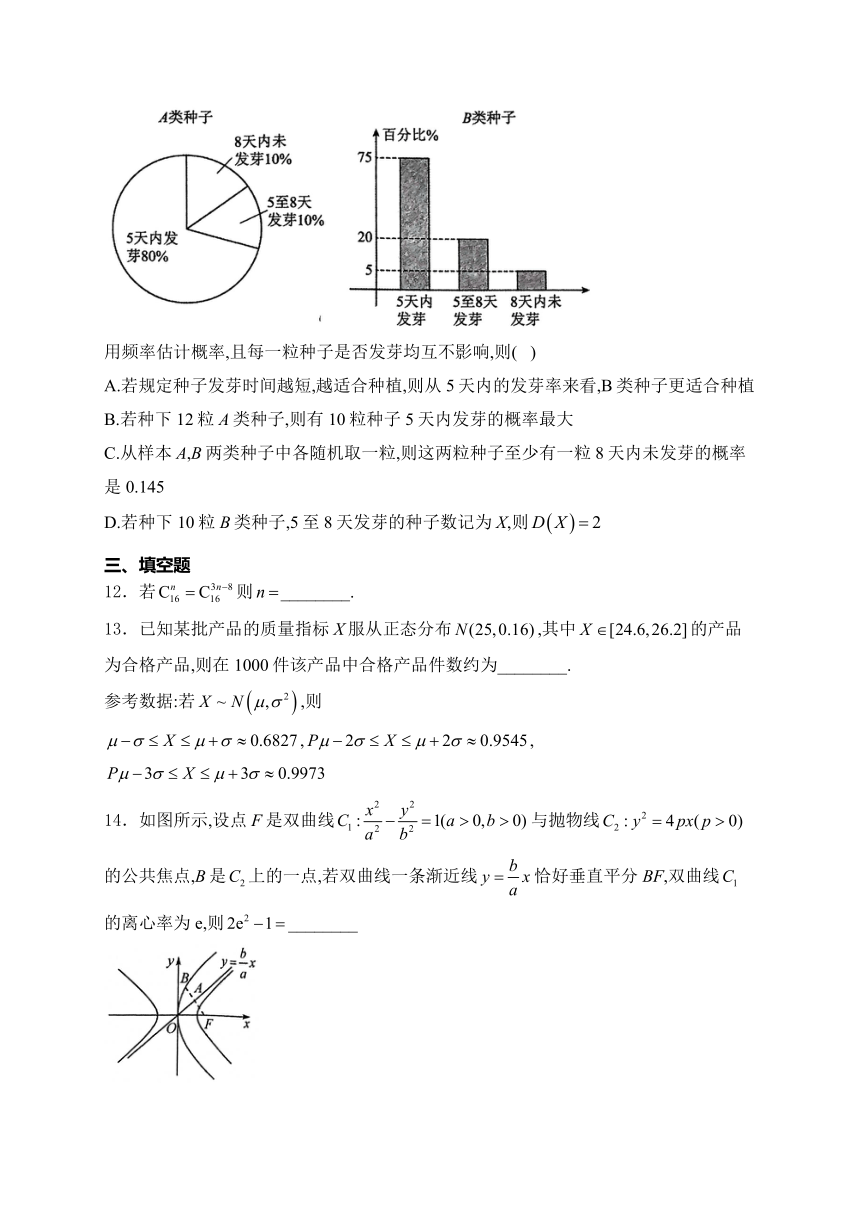
11.某种子站培育出A,B两类种子,为了研究种子的发芽率,分别抽取100粒种子进行试种,得到如下饼状图与柱状图:
用频率估计概率,且每一粒种子是否发芽均互不影响,则( )
A.若规定种子发芽时间越短,越适合种植,则从5天内的发芽率来看,B类种子更适合种植
B.若种下12粒A类种子,则有10粒种子5天内发芽的概率最大
C.从样本A,B两类种子中各随机取一粒,则这两粒种子至少有一粒8天内未发芽的概率是0.145
D.若种下10粒B类种子,5至8天发芽的种子数记为X,则
三、填空题
12.若则________.
13.已知某批产品的质量指标X服从正态分布,其中的产品为合格产品,则在1000件该产品中合格产品件数约为________.
参考数据:若,则,,
14.如图所示,设点F是双曲线与抛物线的公共焦点,B是上的一点,若双曲线一条渐近线恰好垂直平分BF,双曲线的离心率为e,则________
四、解答题
15.已知数列的前n项和为足,.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
16.如图,在四棱锥中,平面ABCD,四边形ABCD为直角梯形,,,,,,Q为PD的中点.
(1)求证:平面平面ABQ;
(2)求二面角的正弦值.
17.将氢储存在甲基环乙烷和甲苯等有机液体中是储氢和运输氢的重要方向.2023年12月俄罗斯科学院西伯利亚分院科研人员用镍和锡取代铂,研发出一种新型高效的脱氢催化剂,脱氢效率达99.9%,且对储氢载体没有破坏作用,可重复使用.近年来,我国氢能源汽车产业迅速发展,下表是某市氢能源乘用车的年销售量与年份的统计表:
年份 2018 2019 2020 2021 2022
年份编号x 1 2 3 4 5
销量y(万台) 2 3.5 2.5 8 9
(1)求y关于x的经验回归方程,并预测2024年氢能源乘用车的销量;
(2)为了研究不同性别的学生对氢能源的了解情况,某校组织了一次有关氢能源的知识竞赛活动,随机抽取了男生和女生各60名,得到如表所示的数据:
了解 不了解 合计
男生 25
女生 20
合计
(i)根据已知条件,填写上述列联表;
(ii)依据的独立性检验,能否认为该校学生对氢能源的了解情况与性别有关 参考公式:
(1)回归方程中斜率和截距的最小二乘法估计公式分别为
,;
(2),
0.050 0.010 0.001
3.841 6.635 10.828
18.中华茶文化源远流长,博大精深,制作复杂.其中绿茶在制茶过程中,在采摘后还需要经过杀青,揉捻,干燥这三道工序.现在某绿茶厂将采摘后的茶叶进行加工,其中杀青,揉捻,干燥这三道工序合格的概率分别为,p,,每道工序的加工都相互独立,且茶叶加工中三道工序至少有一道工序合格的概率为.三道工序加工都合格的绿茶为特级绿茶,恰有两道工序加工合格的绿茶为一级绿茶,恰有一道工序加工合格的绿茶为二级绿茶,其余的为不合格绿茶.
(1)在绿茶的三道工序中恰有两道工序加工合格的前提下,求杀青加工合格的概率;
(2)每盒绿茶(净重100g)原材料及制作成本为30元,其中特级绿茶,一级绿茶,二级绿茶的出厂价分别为90元,60元,40元,而不合格绿茶则不进入市场.记经过三道工序制成的一盒绿茶的利润为X元,求随机变量X的分布列及数学期望.
19.已知函数.
(1)若,求函数在处的切线方程;
(2)讨论函数的单调性;
(3)设求函数在上的零点个数.
参考答案
1.答案:D
解析:,,
又,,
,
,
,
故选:D.
2.答案:B
解析:
3.答案:A
解析:的展开式中的通项,,1,2,…,8.
令,得,故的展开式中含项的系数为.
故选:A.
4.答案:D
解析:
5.答案:C
解析:设抽取的女生人数为X,则X可能取值为0,1,2,
则,,,
所以,
故选:C.
6.答案:C
解析:根据题意,甲,乙都单独1人去某一个景点打卡游玩,
则剩下的4人去其他的两个景点游玩,则其余4位主播有两种情况:
①3位主播去一个景点,1位主播去另外一个景点,有种不同游玩方法,
②分别都是2位主播去一个景点,种不同游玩方法,
则不同游玩方法种.
故选:C.
7.答案:A
解析:
8.答案:B
解析:
9.答案:BD
解析:的展开式中,只有第5项的二项式系数最大,
则第5项为中间项,即,A错误;
令,可得展开式的各项系数之和为,B正确;
展开式的二项式系数之和为,C错误;
在的展开式中,通项,
,1,2,…,8,
令,得,
故展开式中的含项系数是,D正确.
故选:BD.
10.答案:ACD
解析:
11.答案:BC
解析:
12.答案:4或6
解析:
13.答案:840
解析:
14.答案:
解析:
15.答案:(1)见解析
(2)见解析
解析:(1)当时,,所以;
当时,由,则,
可得,
整理得,所以数列是首项为,公差为的等差数列,
故.
(2)由(1)可得:,
则,
,
两式相减得:
,
所以.
16.答案:(1)见解析
(2)
解析:(1)平面ABCD,平面ABCD,
又,,且平面PAD,平面PAD,
平面,又,,
,Q为PD的中点,所以,
又,且平面ABQ,平面ABQ,
平面ABQ,
又面PCD,
平面平面PCD
(2)以A为坐标原点,直线AB,AD,AP分别为x,y,z轴,建立如图所示的空间直角坐标系,
则,,,,,,
所以,,,
设平面ABQ的法向量为,
则,取,则,
设平面BQE的一个法向量为,
则,取,,
则1
所以二面角的正弦值为,
故所求二面角的正弦值为.
17.答案:(1)可以预测2024年氢能源乘用车的销量约为12.4万台
(2)见解析
解析:(1)年份编号的平均数,
销量y的平均数,
所以,
又
,
所以,
于是,
所以y关于x的经验回归方程为,又因为年份2024对应的编号x为7,
所以,
故可以预测2024年氢能源乘用车的销量约为12.4万台.
(2)(ⅰ)根据男生和女生各60名,补全列联表为:
了解 不了解 合计
男生 35 25 60
女生 20 40 60
合计 55 65 120
(ⅱ)零假设:该校学生对氢能源的了解情况与性别无关,
根据列联表中的数据可得:,
依据的独立性检验,可以推断不成立,即该校学生对氢能源的了解情况与性别有关.
18.答案:(1)
(2)
解析:(1)由三道工序至少有一道工序合格的概率为,得,解得
记杀青,揉捻,干燥这三道工序加工合格分别为事件A,B,C,这三道工序加工中恰有两道工序合格记为事件,
则,
,
因此,
所以在绿茶的三道工序中恰有两道工序加工合格的前提下,杀青加工合格的概率为
(2)由题意可知随机变量的所有可能取值为,10,30,60,
则,
,
,
,
则随机变量X的分布列为:
X 10 30 60
P
故X的数学期望为.
19.答案:(1)
(2)见解析
(3)见解析
解析:(1)当时,,,且,
所以在点处的切线斜率
故所求切线方程为,即;
(2)由,所以,
当时,,所以函数在上单调递增;
当时,由,则,若,则,所以在单调递增,
在上单调递减.
综上所述:当时,函数在上单调递增;当时,在单调递增,在上单调递减;
(3)由,所以,
令,由,所以,可得,
原题意等价于与在上的交点个数,
令,则,
令,则,
由,,所以在上单调递增,,即,
故在上递增,
由,所以在上单调递增,所以,
即,
当,即时,与在只有一个交点,此时在上只有一个零点;
当或,即或时,与在无交点,此时在上没有零点;
综上所述:当时,在上只有一个零点;
当或时,在上没有零点.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.设等差数列满足,,则( )
A.80 B.100 C.120 D.160
2.若圆与圆的公共弦长为则( )
A. B. C.2 D.4
3.的展开式中含项的系数为( )
A. B. C.28 D.56
4.5G技术在我国已经进入调整发展的阶段,5G手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:
时间x 1 2 3 4 5
销售量y(千只) 0.5 0.8 1.0 1.2 1.5
若x与y线性相关,且线性回归方程为,则下列说法正确的是( )
A.由题中数据可知,变量y与x正相关,且相关系数
B.当解释变量x每增加1个单位时,预报变量9平均增加个单位
C.线性回归方程中
D.可以预测时,该商场5G手机销量约为1.72(千只)
5.2024年“与辉同行”直播间开播,董宇辉领衔7位主播从“心”出发,其中男性5人,女性3人,现需排班晚8:00黄金档,随机抽取两人,则女生人数的期望为( )
A. B. C. D.
6.甲辰龙年春节哈尔滨火爆出圈,成为春节假期旅游城市中的“顶流”.甲,乙等6名网红主播在哈尔滨的中央大街,冰雪大世界,圣索菲亚教堂,音乐长廊4个景点中选择一个打卡游玩,若每个景点至少有一个主播去打卡游玩,每位主播都会选择一个景点打卡游玩,且甲,乙各单独1人去某一个景点打卡游玩,则不同游玩方法有( )
A.96种 B.132种 C.168种 D.204种
7.质数(primenumber)又称素数,一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则这个数为质数.数学上把相差为2的两个素数叫做“孪生素数”,如:3和5,5和7,…,那么,如果我们在不超过30的自然数中,随机选取两个不同的数,记事件A:这两个数都是素数:事件B:这两个数不是孪生素数,则( )
A. B. C. D.
8.已知函数,,若对任意的,,都有成立,则实数a的取值范围是( )
A. B. C.D.
二、多项选择题
9.对于的展开式中,只有第5项的二项式系数最大,则下列说法正确的是( )
A. B.展开式的各项系数之和为l
C.展开式的二项式系数之和为512 D.展开式中的含项系数是1792
10.定义在上的函数满足,,(若则,c为常数),则下列说法正确的是( )
A.在.处取得极大值,极大值为
B.恰有两个零点
C.若在上恒成立,则
11.某种子站培育出A,B两类种子,为了研究种子的发芽率,分别抽取100粒种子进行试种,得到如下饼状图与柱状图:
用频率估计概率,且每一粒种子是否发芽均互不影响,则( )
A.若规定种子发芽时间越短,越适合种植,则从5天内的发芽率来看,B类种子更适合种植
B.若种下12粒A类种子,则有10粒种子5天内发芽的概率最大
C.从样本A,B两类种子中各随机取一粒,则这两粒种子至少有一粒8天内未发芽的概率是0.145
D.若种下10粒B类种子,5至8天发芽的种子数记为X,则
三、填空题
12.若则________.
13.已知某批产品的质量指标X服从正态分布,其中的产品为合格产品,则在1000件该产品中合格产品件数约为________.
参考数据:若,则,,
14.如图所示,设点F是双曲线与抛物线的公共焦点,B是上的一点,若双曲线一条渐近线恰好垂直平分BF,双曲线的离心率为e,则________
四、解答题
15.已知数列的前n项和为足,.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
16.如图,在四棱锥中,平面ABCD,四边形ABCD为直角梯形,,,,,,Q为PD的中点.
(1)求证:平面平面ABQ;
(2)求二面角的正弦值.
17.将氢储存在甲基环乙烷和甲苯等有机液体中是储氢和运输氢的重要方向.2023年12月俄罗斯科学院西伯利亚分院科研人员用镍和锡取代铂,研发出一种新型高效的脱氢催化剂,脱氢效率达99.9%,且对储氢载体没有破坏作用,可重复使用.近年来,我国氢能源汽车产业迅速发展,下表是某市氢能源乘用车的年销售量与年份的统计表:
年份 2018 2019 2020 2021 2022
年份编号x 1 2 3 4 5
销量y(万台) 2 3.5 2.5 8 9
(1)求y关于x的经验回归方程,并预测2024年氢能源乘用车的销量;
(2)为了研究不同性别的学生对氢能源的了解情况,某校组织了一次有关氢能源的知识竞赛活动,随机抽取了男生和女生各60名,得到如表所示的数据:
了解 不了解 合计
男生 25
女生 20
合计
(i)根据已知条件,填写上述列联表;
(ii)依据的独立性检验,能否认为该校学生对氢能源的了解情况与性别有关 参考公式:
(1)回归方程中斜率和截距的最小二乘法估计公式分别为
,;
(2),
0.050 0.010 0.001
3.841 6.635 10.828
18.中华茶文化源远流长,博大精深,制作复杂.其中绿茶在制茶过程中,在采摘后还需要经过杀青,揉捻,干燥这三道工序.现在某绿茶厂将采摘后的茶叶进行加工,其中杀青,揉捻,干燥这三道工序合格的概率分别为,p,,每道工序的加工都相互独立,且茶叶加工中三道工序至少有一道工序合格的概率为.三道工序加工都合格的绿茶为特级绿茶,恰有两道工序加工合格的绿茶为一级绿茶,恰有一道工序加工合格的绿茶为二级绿茶,其余的为不合格绿茶.
(1)在绿茶的三道工序中恰有两道工序加工合格的前提下,求杀青加工合格的概率;
(2)每盒绿茶(净重100g)原材料及制作成本为30元,其中特级绿茶,一级绿茶,二级绿茶的出厂价分别为90元,60元,40元,而不合格绿茶则不进入市场.记经过三道工序制成的一盒绿茶的利润为X元,求随机变量X的分布列及数学期望.
19.已知函数.
(1)若,求函数在处的切线方程;
(2)讨论函数的单调性;
(3)设求函数在上的零点个数.
参考答案
1.答案:D
解析:,,
又,,
,
,
,
故选:D.
2.答案:B
解析:
3.答案:A
解析:的展开式中的通项,,1,2,…,8.
令,得,故的展开式中含项的系数为.
故选:A.
4.答案:D
解析:
5.答案:C
解析:设抽取的女生人数为X,则X可能取值为0,1,2,
则,,,
所以,
故选:C.
6.答案:C
解析:根据题意,甲,乙都单独1人去某一个景点打卡游玩,
则剩下的4人去其他的两个景点游玩,则其余4位主播有两种情况:
①3位主播去一个景点,1位主播去另外一个景点,有种不同游玩方法,
②分别都是2位主播去一个景点,种不同游玩方法,
则不同游玩方法种.
故选:C.
7.答案:A
解析:
8.答案:B
解析:
9.答案:BD
解析:的展开式中,只有第5项的二项式系数最大,
则第5项为中间项,即,A错误;
令,可得展开式的各项系数之和为,B正确;
展开式的二项式系数之和为,C错误;
在的展开式中,通项,
,1,2,…,8,
令,得,
故展开式中的含项系数是,D正确.
故选:BD.
10.答案:ACD
解析:
11.答案:BC
解析:
12.答案:4或6
解析:
13.答案:840
解析:
14.答案:
解析:
15.答案:(1)见解析
(2)见解析
解析:(1)当时,,所以;
当时,由,则,
可得,
整理得,所以数列是首项为,公差为的等差数列,
故.
(2)由(1)可得:,
则,
,
两式相减得:
,
所以.
16.答案:(1)见解析
(2)
解析:(1)平面ABCD,平面ABCD,
又,,且平面PAD,平面PAD,
平面,又,,
,Q为PD的中点,所以,
又,且平面ABQ,平面ABQ,
平面ABQ,
又面PCD,
平面平面PCD
(2)以A为坐标原点,直线AB,AD,AP分别为x,y,z轴,建立如图所示的空间直角坐标系,
则,,,,,,
所以,,,
设平面ABQ的法向量为,
则,取,则,
设平面BQE的一个法向量为,
则,取,,
则1
所以二面角的正弦值为,
故所求二面角的正弦值为.
17.答案:(1)可以预测2024年氢能源乘用车的销量约为12.4万台
(2)见解析
解析:(1)年份编号的平均数,
销量y的平均数,
所以,
又
,
所以,
于是,
所以y关于x的经验回归方程为,又因为年份2024对应的编号x为7,
所以,
故可以预测2024年氢能源乘用车的销量约为12.4万台.
(2)(ⅰ)根据男生和女生各60名,补全列联表为:
了解 不了解 合计
男生 35 25 60
女生 20 40 60
合计 55 65 120
(ⅱ)零假设:该校学生对氢能源的了解情况与性别无关,
根据列联表中的数据可得:,
依据的独立性检验,可以推断不成立,即该校学生对氢能源的了解情况与性别有关.
18.答案:(1)
(2)
解析:(1)由三道工序至少有一道工序合格的概率为,得,解得
记杀青,揉捻,干燥这三道工序加工合格分别为事件A,B,C,这三道工序加工中恰有两道工序合格记为事件,
则,
,
因此,
所以在绿茶的三道工序中恰有两道工序加工合格的前提下,杀青加工合格的概率为
(2)由题意可知随机变量的所有可能取值为,10,30,60,
则,
,
,
,
则随机变量X的分布列为:
X 10 30 60
P
故X的数学期望为.
19.答案:(1)
(2)见解析
(3)见解析
解析:(1)当时,,,且,
所以在点处的切线斜率
故所求切线方程为,即;
(2)由,所以,
当时,,所以函数在上单调递增;
当时,由,则,若,则,所以在单调递增,
在上单调递减.
综上所述:当时,函数在上单调递增;当时,在单调递增,在上单调递减;
(3)由,所以,
令,由,所以,可得,
原题意等价于与在上的交点个数,
令,则,
令,则,
由,,所以在上单调递增,,即,
故在上递增,
由,所以在上单调递增,所以,
即,
当,即时,与在只有一个交点,此时在上只有一个零点;
当或,即或时,与在无交点,此时在上没有零点;
综上所述:当时,在上只有一个零点;
当或时,在上没有零点.
同课章节目录
