苏科版八年级数学上册 1.2全等三角形试题(含详解)
文档属性
| 名称 | 苏科版八年级数学上册 1.2全等三角形试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 732.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 16:04:47 | ||
图片预览


文档简介
1.2全等三角形
一、单选题
1.下列说法:①两个形状相同的图形称为全等图形;②边、角分别对应相等的两个多边形全等;③全等图形的形状、大小都相同;④面积相等的两个三角形全等.其中正确的是( )
A.①②③ B.①②④ C.①③ D.②③
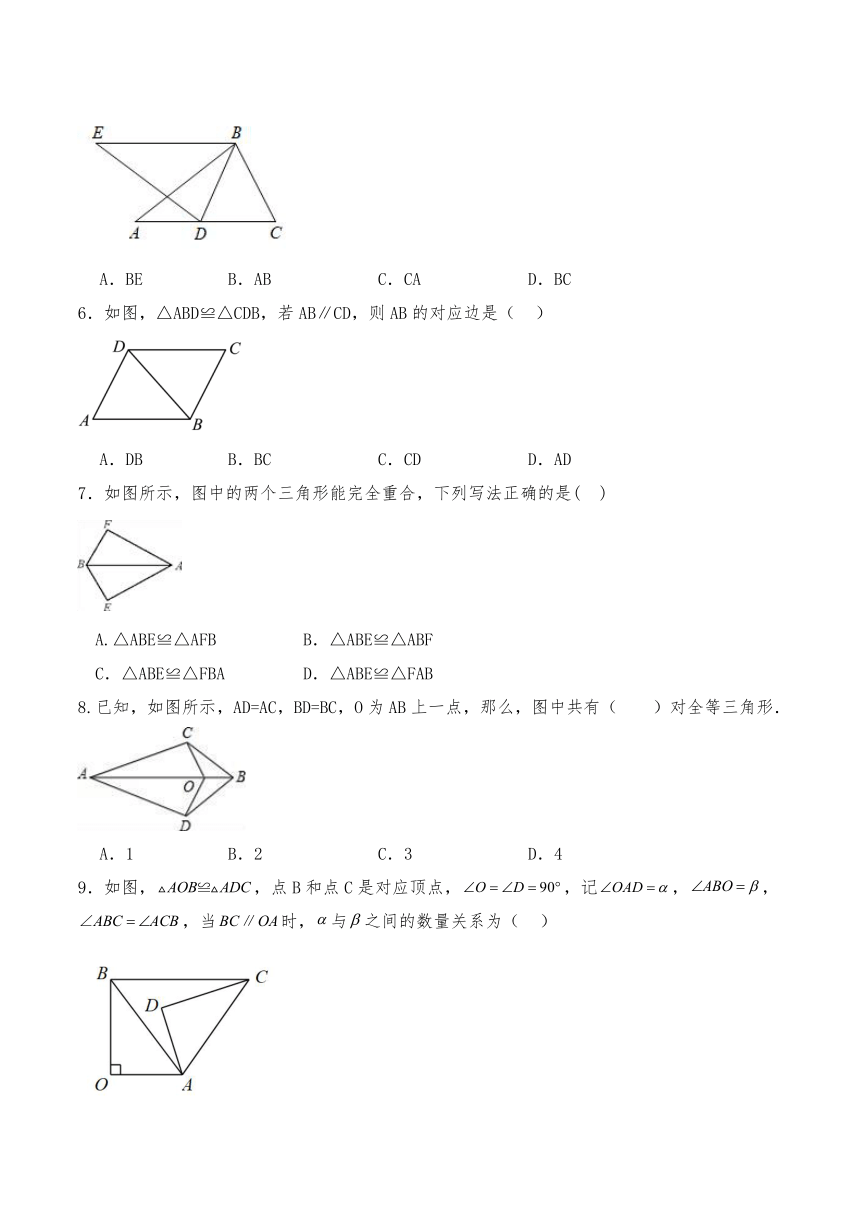
2.如图,若,四个点B、E、C、F在同一直线上,,则的长是( )
A.2 B.3 C.5 D.7
3.已知图中的两个三角形全等,则的度数是( )
A. B. C. D.
4.以下四组图形中,与如下图形全等的是( )
A. B. C. D.
5.如图,两个三角形△ABC与△BDE全等,观察图形,判断在这两个三角形中边DE的对应边为( )
A.BE B.AB C.CA D.BC
6.如图,△ABD≌△CDB,若AB∥CD,则AB的对应边是( )
A.DB B.BC C.CD D.AD
7.如图所示,图中的两个三角形能完全重合,下列写法正确的是( )
A.△ABE≌△AFB B.△ABE≌△ABF
C.△ABE≌△FBA D.△ABE≌△FAB
8.已知,如图所示,AD=AC,BD=BC,O为AB上一点,那么,图中共有( )对全等三角形.
A.1 B.2 C.3 D.4
9.如图,,点B和点C是对应顶点,,记,,,当时,与之间的数量关系为( )
A. B. C. D.
10.如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边;②AC与CA是对应边;③点A与点A是对应顶点;④点C与点C是对应顶点;⑤∠ACB与∠CAD是对应角,
其中正确的是( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.能够完全重合的两个图形叫做 .如果两个图形全等.它们的形状和大小一定 .
12.如图,,,,则的度数是 .
13.如图,,,,,则 .
14.如图,已知,,则的度数为 .
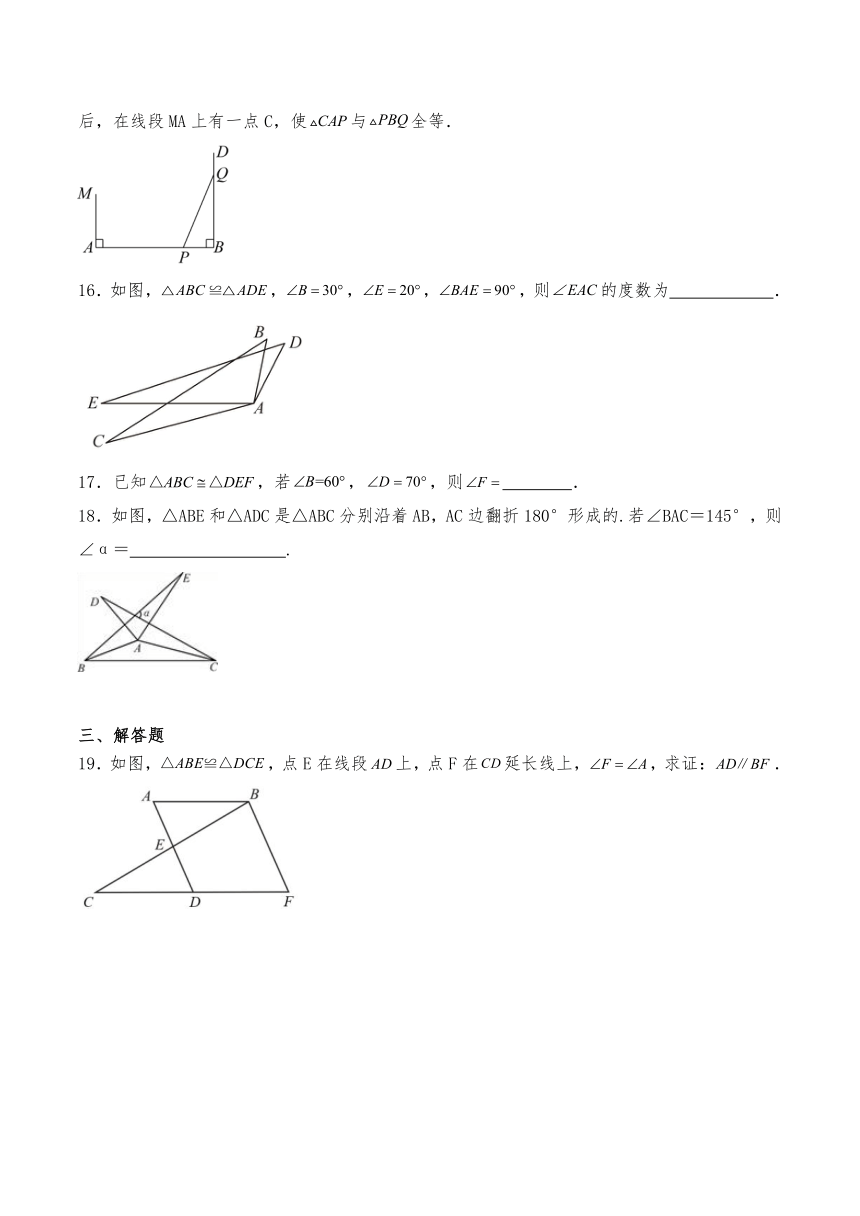
15.如图,已知线段,于点A,,射线于B,P点从B点向A运动,每秒走1m,Q点从B点向D运动,每秒走3m,P,Q同时从B出发,则出发 秒后,在线段MA上有一点C,使与全等.
16.如图,,,,,则的度数为 .
17.已知,若,,则 .
18.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠BAC=145°,则∠α= .
三、解答题
19.如图,,点E在线段上,点F在延长线上,,求证:.
20.如图所示,A,D,E三点在同一直线上,且,求证:.
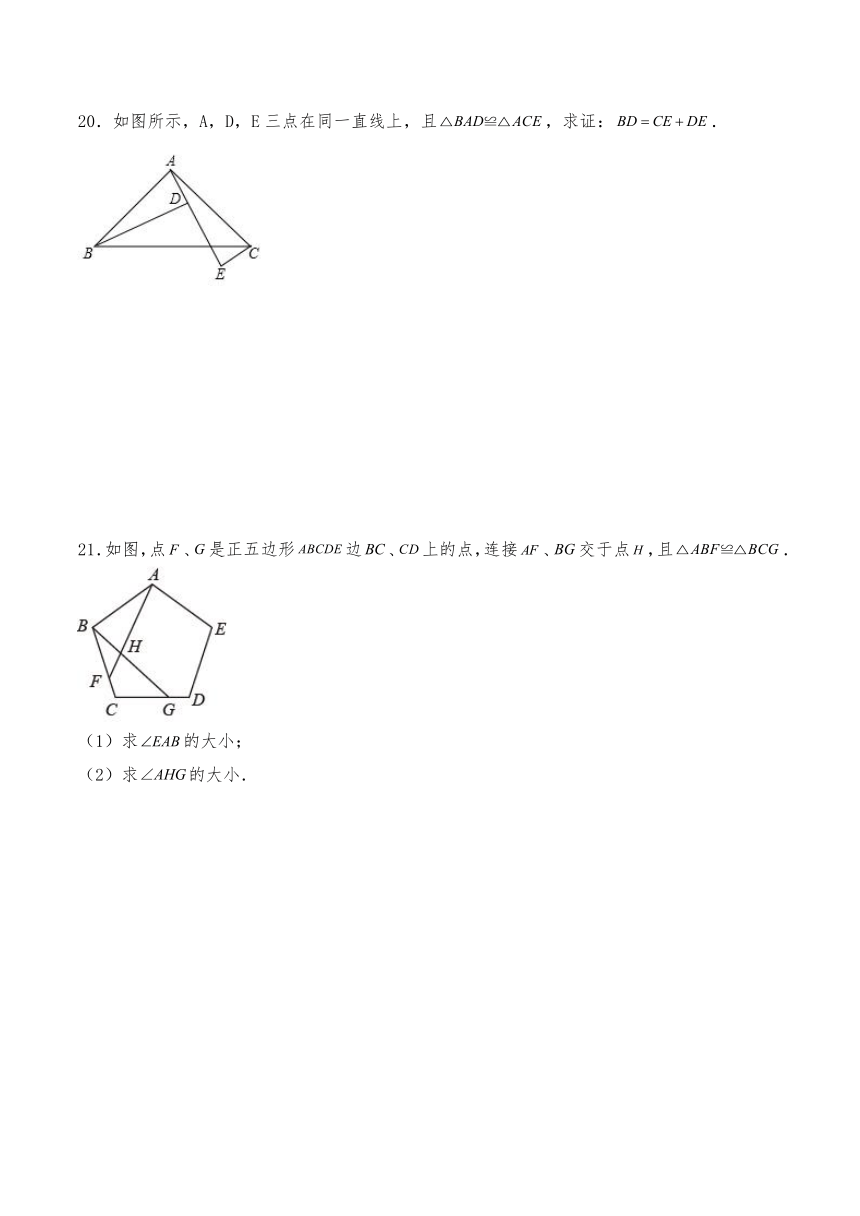
21.如图,点、是正五边形边、上的点,连接、交于点,且.
(1)求的大小;
(2)求的大小.
22.如图,已知,且点B,C,D在同一条直线上,延长交于点F.
(1)求证:;
(2)已知,,求的长度.
23.如图,点A、D、C、B在同一条直线上,,∠B=33°,,BC=5cm,CD=2cm.求:
(1)的度数;
(2)AC的长.
24.如图,已知,平分,若,,求的度数.
25.如图,已知.
(1)若,,求的度数;
(2)若,求的长.
26.如图,已知四边形ABCD中,AB=BC=8cm,CD=6cm,∠B=∠C,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,点Q运动的速度是每秒2cm,点P运动的速度是每秒acm(a≤2),当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒,
(1)BQ= ;BP= ;(用含a或t的代数式表示)
(2)运动过程中,连接PQ、DQ,△BPQ与△CDQ是否全等?若能,请求出相应的t和a的值;若不能,请说明理由.
27.如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图①,当P在BC上,t= 时,△APC的面积等于△ABC面积的一半;
(2)如图②,在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止,在两点运动过程中的某一时刻,恰好△APQ与△DEF全等,求点Q的运动速度.
答案
一、单选题
1.D
【详解】①两个形状相同的图形称为全等图形,说法错误;
②边、角分别对应相等的两个多边形全等,说法正确;
③全等图形的形状、大小都相同,说法正确;
④面积相等的两个三角形是全等图形,说法错误,
2.A
【详解】解:∵,
∴,
又,
∴,
∵,
∵.
3.D
【详解】解:∵如图,两个三角形全等,与的角是、边的夹角,
∴的度数是.
4.B
【详解】解:由全等形的概念结合图形可知:A、C、D中图形形状与题干中已给的图形不一致,故不符合题意;B中的图形可以由题干中已给的图形顺时针或逆时针旋转得到.
5.B
【详解】观察图形可知:BE>AB,BE>BC,∴BE和AC是对应边,显然BD和BC是对应边,∴DE 和AB是对应边.
6.C
【详解】∵AB∥CD,
∴∠CDB=∠ABD,
∴这两个角为对应角,对应角所对的边为对应边,
∴BC和DA为对应边,
∴AB的对应边为CD.
7.B
【详解】解:要把对应顶点写在对应位置.∵B和B对应,A和A对应,E和F对应,故△ABE≌△ABF.
8.C
【详解】△ACO和△ADO,△ADB和△ACB,△COB和△DOB全等,
9.B
【详解】解:,,
,
,,
,,
,
,
化简得:.
10.B
【详解】解:△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D.
①AB与CD是对应边.故①正确;
②AC与CA是对应边.故②正确;
③点A与点C是对应顶点.故③错误;
④点C与点A是对应顶点.故④错误;
⑤∠ACB与∠CAD是对应角.故⑤正确.
综上所述,正确的结论是①②⑤,共有3个.
二、填空题
11. 全等形 相等
12.
【详解】解:∵,
∴,
∴.
13.
【详解】解:∵,,
∴,
∵,
∴,
∴,
14.
【分析】先根据三角形内角和定理求出,再由全等三角形的性质即可得到.
【详解】解:∵,
∴,
∵,
∴,
15.5
【详解】解:当时,,即,
解得:;
当时,米,
此时所用时间为10,,不合题意,舍去;
综上,出发5秒后,在线段上有一点,使与全等.
16.
【详解】解:,
,,
,
,
,
,
,
17.
【详解】解:,
,
在中,,
.
又,
,
18.70°
∴∠BAE=∠BAC=145°,∠DAC=∠BAC=145°,∠E=∠ACD=∠ACB,
∴∠DAE=∠BAC+∠BAE+∠DAC-360°=145°+145°+145°-360°=75°,
∴∠EAC=∠DAC-∠DAE=145°-75°=70°,
∵∠E+∠α+∠EMD=180°,∠EAC+∠AMC+∠ACD=180°,∠EMD=∠AMC,
∴∠α=∠EAC=70°,
三、解答题
19.解: ,
∴∠A=∠CDE
,
∴∠CDE=∠F
∴AD∥BF
20.证明:,
,,
,
.
21.解:(1)五边形是正变形
(2)
,
又
22.(1)证明:∵,
∴,.
∵点B,C,D在同一条直线上,
∴,
∴.
∵,
∴,
∴,即;
(2)∵,
∴,,
∴
∴,
∴.
23.(1)解:∵,,
∴,
∵,,
∴.
(2)解:∵,BC=5cm,
∴AD=BC=5cm,
∵CD=2cm,
∴AC=AD+CD=7cm.
24.∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
25.(1)解:∵,
∴,
∵,
∴,
∵,
∴;
(2)解:∵,
∴,
∴,
即,
∵
∴,
∴.
26.解:(1)由题意得,AP=atcm,BP=(8﹣at)cm,BQ=2tcm,
故答案为:2tcm,(8﹣at)cm;
(2)△BPQ与△CDQ能全等;
∵∠B=∠C,
∴△BPQ与△CDQ全等存在两种情况:
①当△PBQ≌△QCD时,PB=CQ,BQ=CD,
∴2t=6,8﹣at=8﹣2t,
∴a=2,t=3;
②当△PBQ≌△DCQ时,PB=DC,BQ=CQ,
∴8﹣at=6,2t=8﹣2t,
∴a=1,t=2;
综上,△BPQ与△CDQ能全等,此时a=2,t=3或a=1,t=2.
27.(1)解:,
∵△APC的面积等于△ABC面积的一半,
,
当P点运动到BC边上时,此时,
即,
,
此时,
当P点运动到AB边上时,
此时,
∵△APC的边AP上的高与△ABC的边AB上的高相等,
∴,
∴此时P点在AB边的中点,
此时,
综上所述,当t=或时,△APC的面积等于△ABC面积的一半;
(2)设点Q的运动速度为xcm/s,
①当点P在AC上,点Q在AB上,△APQ≌△DEF时,
AP=DE=4cm,AQ=DF=5cm,
∴4÷3=5÷x
解得x=cm/s;
②当点P在AC上,点Q在AB上,△APQ≌△DFE时,
AP=DF =5cm,AQ=DE=4cm,
∴5÷3=4÷x,
解得x=cm/s;
③当点P在AB上,点Q在AC上,△AQP≌△DEF时,
AP=DF=5cm,AQ=DE=4cm,
∴点P的路程为9+12+15-5=31cm,点Q的路程为9+12+15-4=32cm,
∴31÷3=32÷x
解得x=cm/s;
④当点P在AB上,点Q在AC上,△APQ≌△DEF时
AP=DE=4cm,AQ=DF=5cm,
∴点P的路程为9+12+15-4=32cm,点Q的路程为9+12+15-5=31cm,
∴32 ÷3=31÷x
解得x=cm/s;
∴Q运动的速度为cm/s或cm/s或cm/s或cm/s.
一、单选题
1.下列说法:①两个形状相同的图形称为全等图形;②边、角分别对应相等的两个多边形全等;③全等图形的形状、大小都相同;④面积相等的两个三角形全等.其中正确的是( )
A.①②③ B.①②④ C.①③ D.②③
2.如图,若,四个点B、E、C、F在同一直线上,,则的长是( )
A.2 B.3 C.5 D.7
3.已知图中的两个三角形全等,则的度数是( )
A. B. C. D.
4.以下四组图形中,与如下图形全等的是( )
A. B. C. D.
5.如图,两个三角形△ABC与△BDE全等,观察图形,判断在这两个三角形中边DE的对应边为( )
A.BE B.AB C.CA D.BC
6.如图,△ABD≌△CDB,若AB∥CD,则AB的对应边是( )
A.DB B.BC C.CD D.AD
7.如图所示,图中的两个三角形能完全重合,下列写法正确的是( )
A.△ABE≌△AFB B.△ABE≌△ABF
C.△ABE≌△FBA D.△ABE≌△FAB
8.已知,如图所示,AD=AC,BD=BC,O为AB上一点,那么,图中共有( )对全等三角形.
A.1 B.2 C.3 D.4
9.如图,,点B和点C是对应顶点,,记,,,当时,与之间的数量关系为( )
A. B. C. D.
10.如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边;②AC与CA是对应边;③点A与点A是对应顶点;④点C与点C是对应顶点;⑤∠ACB与∠CAD是对应角,
其中正确的是( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.能够完全重合的两个图形叫做 .如果两个图形全等.它们的形状和大小一定 .
12.如图,,,,则的度数是 .
13.如图,,,,,则 .
14.如图,已知,,则的度数为 .
15.如图,已知线段,于点A,,射线于B,P点从B点向A运动,每秒走1m,Q点从B点向D运动,每秒走3m,P,Q同时从B出发,则出发 秒后,在线段MA上有一点C,使与全等.
16.如图,,,,,则的度数为 .
17.已知,若,,则 .
18.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠BAC=145°,则∠α= .
三、解答题
19.如图,,点E在线段上,点F在延长线上,,求证:.
20.如图所示,A,D,E三点在同一直线上,且,求证:.
21.如图,点、是正五边形边、上的点,连接、交于点,且.
(1)求的大小;
(2)求的大小.
22.如图,已知,且点B,C,D在同一条直线上,延长交于点F.
(1)求证:;
(2)已知,,求的长度.
23.如图,点A、D、C、B在同一条直线上,,∠B=33°,,BC=5cm,CD=2cm.求:
(1)的度数;
(2)AC的长.
24.如图,已知,平分,若,,求的度数.
25.如图,已知.
(1)若,,求的度数;
(2)若,求的长.
26.如图,已知四边形ABCD中,AB=BC=8cm,CD=6cm,∠B=∠C,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,点Q运动的速度是每秒2cm,点P运动的速度是每秒acm(a≤2),当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒,
(1)BQ= ;BP= ;(用含a或t的代数式表示)
(2)运动过程中,连接PQ、DQ,△BPQ与△CDQ是否全等?若能,请求出相应的t和a的值;若不能,请说明理由.
27.如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图①,当P在BC上,t= 时,△APC的面积等于△ABC面积的一半;
(2)如图②,在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止,在两点运动过程中的某一时刻,恰好△APQ与△DEF全等,求点Q的运动速度.
答案
一、单选题
1.D
【详解】①两个形状相同的图形称为全等图形,说法错误;
②边、角分别对应相等的两个多边形全等,说法正确;
③全等图形的形状、大小都相同,说法正确;
④面积相等的两个三角形是全等图形,说法错误,
2.A
【详解】解:∵,
∴,
又,
∴,
∵,
∵.
3.D
【详解】解:∵如图,两个三角形全等,与的角是、边的夹角,
∴的度数是.
4.B
【详解】解:由全等形的概念结合图形可知:A、C、D中图形形状与题干中已给的图形不一致,故不符合题意;B中的图形可以由题干中已给的图形顺时针或逆时针旋转得到.
5.B
【详解】观察图形可知:BE>AB,BE>BC,∴BE和AC是对应边,显然BD和BC是对应边,∴DE 和AB是对应边.
6.C
【详解】∵AB∥CD,
∴∠CDB=∠ABD,
∴这两个角为对应角,对应角所对的边为对应边,
∴BC和DA为对应边,
∴AB的对应边为CD.
7.B
【详解】解:要把对应顶点写在对应位置.∵B和B对应,A和A对应,E和F对应,故△ABE≌△ABF.
8.C
【详解】△ACO和△ADO,△ADB和△ACB,△COB和△DOB全等,
9.B
【详解】解:,,
,
,,
,,
,
,
化简得:.
10.B
【详解】解:△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D.
①AB与CD是对应边.故①正确;
②AC与CA是对应边.故②正确;
③点A与点C是对应顶点.故③错误;
④点C与点A是对应顶点.故④错误;
⑤∠ACB与∠CAD是对应角.故⑤正确.
综上所述,正确的结论是①②⑤,共有3个.
二、填空题
11. 全等形 相等
12.
【详解】解:∵,
∴,
∴.
13.
【详解】解:∵,,
∴,
∵,
∴,
∴,
14.
【分析】先根据三角形内角和定理求出,再由全等三角形的性质即可得到.
【详解】解:∵,
∴,
∵,
∴,
15.5
【详解】解:当时,,即,
解得:;
当时,米,
此时所用时间为10,,不合题意,舍去;
综上,出发5秒后,在线段上有一点,使与全等.
16.
【详解】解:,
,,
,
,
,
,
,
17.
【详解】解:,
,
在中,,
.
又,
,
18.70°
∴∠BAE=∠BAC=145°,∠DAC=∠BAC=145°,∠E=∠ACD=∠ACB,
∴∠DAE=∠BAC+∠BAE+∠DAC-360°=145°+145°+145°-360°=75°,
∴∠EAC=∠DAC-∠DAE=145°-75°=70°,
∵∠E+∠α+∠EMD=180°,∠EAC+∠AMC+∠ACD=180°,∠EMD=∠AMC,
∴∠α=∠EAC=70°,
三、解答题
19.解: ,
∴∠A=∠CDE
,
∴∠CDE=∠F
∴AD∥BF
20.证明:,
,,
,
.
21.解:(1)五边形是正变形
(2)
,
又
22.(1)证明:∵,
∴,.
∵点B,C,D在同一条直线上,
∴,
∴.
∵,
∴,
∴,即;
(2)∵,
∴,,
∴
∴,
∴.
23.(1)解:∵,,
∴,
∵,,
∴.
(2)解:∵,BC=5cm,
∴AD=BC=5cm,
∵CD=2cm,
∴AC=AD+CD=7cm.
24.∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
25.(1)解:∵,
∴,
∵,
∴,
∵,
∴;
(2)解:∵,
∴,
∴,
即,
∵
∴,
∴.
26.解:(1)由题意得,AP=atcm,BP=(8﹣at)cm,BQ=2tcm,
故答案为:2tcm,(8﹣at)cm;
(2)△BPQ与△CDQ能全等;
∵∠B=∠C,
∴△BPQ与△CDQ全等存在两种情况:
①当△PBQ≌△QCD时,PB=CQ,BQ=CD,
∴2t=6,8﹣at=8﹣2t,
∴a=2,t=3;
②当△PBQ≌△DCQ时,PB=DC,BQ=CQ,
∴8﹣at=6,2t=8﹣2t,
∴a=1,t=2;
综上,△BPQ与△CDQ能全等,此时a=2,t=3或a=1,t=2.
27.(1)解:,
∵△APC的面积等于△ABC面积的一半,
,
当P点运动到BC边上时,此时,
即,
,
此时,
当P点运动到AB边上时,
此时,
∵△APC的边AP上的高与△ABC的边AB上的高相等,
∴,
∴此时P点在AB边的中点,
此时,
综上所述,当t=或时,△APC的面积等于△ABC面积的一半;
(2)设点Q的运动速度为xcm/s,
①当点P在AC上,点Q在AB上,△APQ≌△DEF时,
AP=DE=4cm,AQ=DF=5cm,
∴4÷3=5÷x
解得x=cm/s;
②当点P在AC上,点Q在AB上,△APQ≌△DFE时,
AP=DF =5cm,AQ=DE=4cm,
∴5÷3=4÷x,
解得x=cm/s;
③当点P在AB上,点Q在AC上,△AQP≌△DEF时,
AP=DF=5cm,AQ=DE=4cm,
∴点P的路程为9+12+15-5=31cm,点Q的路程为9+12+15-4=32cm,
∴31÷3=32÷x
解得x=cm/s;
④当点P在AB上,点Q在AC上,△APQ≌△DEF时
AP=DE=4cm,AQ=DF=5cm,
∴点P的路程为9+12+15-4=32cm,点Q的路程为9+12+15-5=31cm,
∴32 ÷3=31÷x
解得x=cm/s;
∴Q运动的速度为cm/s或cm/s或cm/s或cm/s.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
