11.3.2 直线,平面平行的判定与性质 教案
文档属性
| 名称 | 11.3.2 直线,平面平行的判定与性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 433.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 00:00:00 | ||
图片预览

文档简介
直线、平面平行的判定与性质(一) 教案
一、学习目标
知识与技能:
1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行、面面平行的有关的判定定理与性质定理。
2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题。
能力目标:
学生通过观察图形,借助已有知识,掌握直线与平面平行,平面与平面平行的判定与性质的应用。
情感目标:
1.让学生在发现中学习,增强学习的积极性。
2.让学生了解空间与平面互相转换的数学思想,直线与平面的位置关系,直线与平面平行的判定与性质,平面与平面平行的判定与性质。
二、重点难点
重点:直线与平面平行、平面与平面平行的判定和性质定理及应用。
难点:灵活的运用数学证明思想。
三、教学方法
启发式、引导式,、多注重观察和分析
四、教学过程
(一)知识梳理
直线与平面平行的判定定理与性质定理
判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与
此平面平行(简记为“线线平行 线面平行”)
图像语言: 符号语言:
性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,
那么该直线与交线平行(简记为“线面平行 线线平行”)
图形语言: 符号语言:
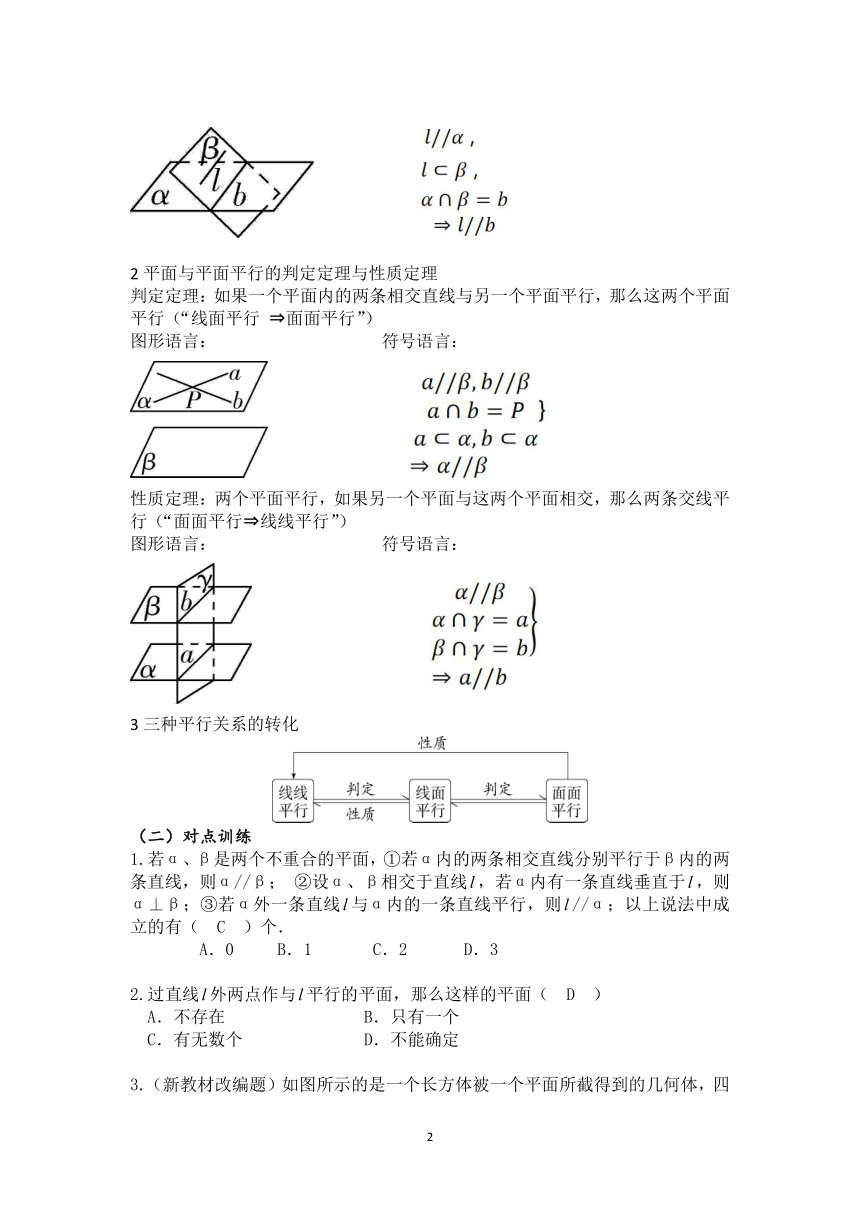
2平面与平面平行的判定定理与性质定理
判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行(“线面平行 面面平行”)
图形语言: 符号语言:
性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行(“面面平行 线线平行”)
图形语言: 符号语言:
3三种平行关系的转化
(二)对点训练
1.若α、β是两个不重合的平面,①若α内的两条相交直线分别平行于β内的两条直线,则α//β; ②设α、β相交于直线,若α内有一条直线垂直于,则α⊥β;③若α外一条直线与α内的一条直线平行,则//α;以上说法中成立的有( C )个.
A.0 B.1 C.2 D.3
2.过直线外两点作与平行的平面,那么这样的平面( D )
A.不存在 B.只有一个
C.有无数个 D.不能确定
3.(新教材改编题)如图所示的是一个长方体被一个平面所截得到的几何体,四边形 EFGH为截面,则四边形 EFGH的形状为__平行四边形__________.
(三)关键能力突破
例1.如图,四面体ABCD被一平面所截,截面EFGH为平行四边形,
求证:CD//平面EFGH
例2. 如图,在正方形ABCD和正方形ADEF中,M、N分别是对角线AE、BD上的点,且AM=BN。求证:MN//平面EDC
方法一:连接AN并延长与DC的延长线交于G点,
连接EG,证明MN//EG.
方法二:过M点作MF//AD交ED于H,过N点作
NK//BC交DC于J,连接HJ.证明MN//HJ
方法三:作ML//ED交AD于L,连接LN,证明
平面MNL//平面EDC
方法感悟:
(四)练习
1.设α,β为两个平面,则α//β的充要条件是( B )
A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行
C.α,β平行于同一条直线 D.α,β垂直于同一平面
2.如图,已知正方体ABCD ,M,N分别是的中点,则( A )
A.直线与直线垂直,直线MN//平面ABCD
B.直线与直线平行,直线MN⊥平面
C.直线与直线相交,直线MN//平面ABCD
D.直线与直线异面,直线MN⊥平面
3. 在正方体ABCD 中,E,F分别为AB,BC的中点,则( A )
A.平面⊥平面 B.平面⊥平面
C.平面//平面 D.平面//平面
作业
1.如图,在正方体 中,分别为对角线 上的点,且
(1) 求证: ;
(2) 若 上的点, 的值为多少时,
能使平面 ?请给出证明
如图所示,平面 ,点 ,点 ,点 ,点 ,点 分别在线段 , 上,且 .
(1) 求证: ;
(2) 若分别是 的中点, , ,且所成的角为 , 求 的长.
解:因为EF//HG
HG 平面BCD
EF 平面BCD
所以EF//平面BCD
又因为FE 平面ACD
平面ACD∩平面BCD=CD
所以CD//EF
EF 平面EFGH
CD 平面EFGH
所以DC//平面EFGH
一、学习目标
知识与技能:
1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行、面面平行的有关的判定定理与性质定理。
2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题。
能力目标:
学生通过观察图形,借助已有知识,掌握直线与平面平行,平面与平面平行的判定与性质的应用。
情感目标:
1.让学生在发现中学习,增强学习的积极性。
2.让学生了解空间与平面互相转换的数学思想,直线与平面的位置关系,直线与平面平行的判定与性质,平面与平面平行的判定与性质。
二、重点难点
重点:直线与平面平行、平面与平面平行的判定和性质定理及应用。
难点:灵活的运用数学证明思想。
三、教学方法
启发式、引导式,、多注重观察和分析
四、教学过程
(一)知识梳理
直线与平面平行的判定定理与性质定理
判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与
此平面平行(简记为“线线平行 线面平行”)
图像语言: 符号语言:
性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,
那么该直线与交线平行(简记为“线面平行 线线平行”)
图形语言: 符号语言:
2平面与平面平行的判定定理与性质定理
判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行(“线面平行 面面平行”)
图形语言: 符号语言:
性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行(“面面平行 线线平行”)
图形语言: 符号语言:
3三种平行关系的转化
(二)对点训练
1.若α、β是两个不重合的平面,①若α内的两条相交直线分别平行于β内的两条直线,则α//β; ②设α、β相交于直线,若α内有一条直线垂直于,则α⊥β;③若α外一条直线与α内的一条直线平行,则//α;以上说法中成立的有( C )个.
A.0 B.1 C.2 D.3
2.过直线外两点作与平行的平面,那么这样的平面( D )
A.不存在 B.只有一个
C.有无数个 D.不能确定
3.(新教材改编题)如图所示的是一个长方体被一个平面所截得到的几何体,四边形 EFGH为截面,则四边形 EFGH的形状为__平行四边形__________.
(三)关键能力突破
例1.如图,四面体ABCD被一平面所截,截面EFGH为平行四边形,
求证:CD//平面EFGH
例2. 如图,在正方形ABCD和正方形ADEF中,M、N分别是对角线AE、BD上的点,且AM=BN。求证:MN//平面EDC
方法一:连接AN并延长与DC的延长线交于G点,
连接EG,证明MN//EG.
方法二:过M点作MF//AD交ED于H,过N点作
NK//BC交DC于J,连接HJ.证明MN//HJ
方法三:作ML//ED交AD于L,连接LN,证明
平面MNL//平面EDC
方法感悟:
(四)练习
1.设α,β为两个平面,则α//β的充要条件是( B )
A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行
C.α,β平行于同一条直线 D.α,β垂直于同一平面
2.如图,已知正方体ABCD ,M,N分别是的中点,则( A )
A.直线与直线垂直,直线MN//平面ABCD
B.直线与直线平行,直线MN⊥平面
C.直线与直线相交,直线MN//平面ABCD
D.直线与直线异面,直线MN⊥平面
3. 在正方体ABCD 中,E,F分别为AB,BC的中点,则( A )
A.平面⊥平面 B.平面⊥平面
C.平面//平面 D.平面//平面
作业
1.如图,在正方体 中,分别为对角线 上的点,且
(1) 求证: ;
(2) 若 上的点, 的值为多少时,
能使平面 ?请给出证明
如图所示,平面 ,点 ,点 ,点 ,点 ,点 分别在线段 , 上,且 .
(1) 求证: ;
(2) 若分别是 的中点, , ,且所成的角为 , 求 的长.
解:因为EF//HG
HG 平面BCD
EF 平面BCD
所以EF//平面BCD
又因为FE 平面ACD
平面ACD∩平面BCD=CD
所以CD//EF
EF 平面EFGH
CD 平面EFGH
所以DC//平面EFGH
