长方体和正方体的体积预习讲义(思维导图、易错例题、针对性训练)数学六年级上册苏教版
文档属性
| 名称 | 长方体和正方体的体积预习讲义(思维导图、易错例题、针对性训练)数学六年级上册苏教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 453.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 16:54:02 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
长方体和正方体的体积预习讲义(思维导图、易错例题、针对性训练)数学六年级上册苏教版
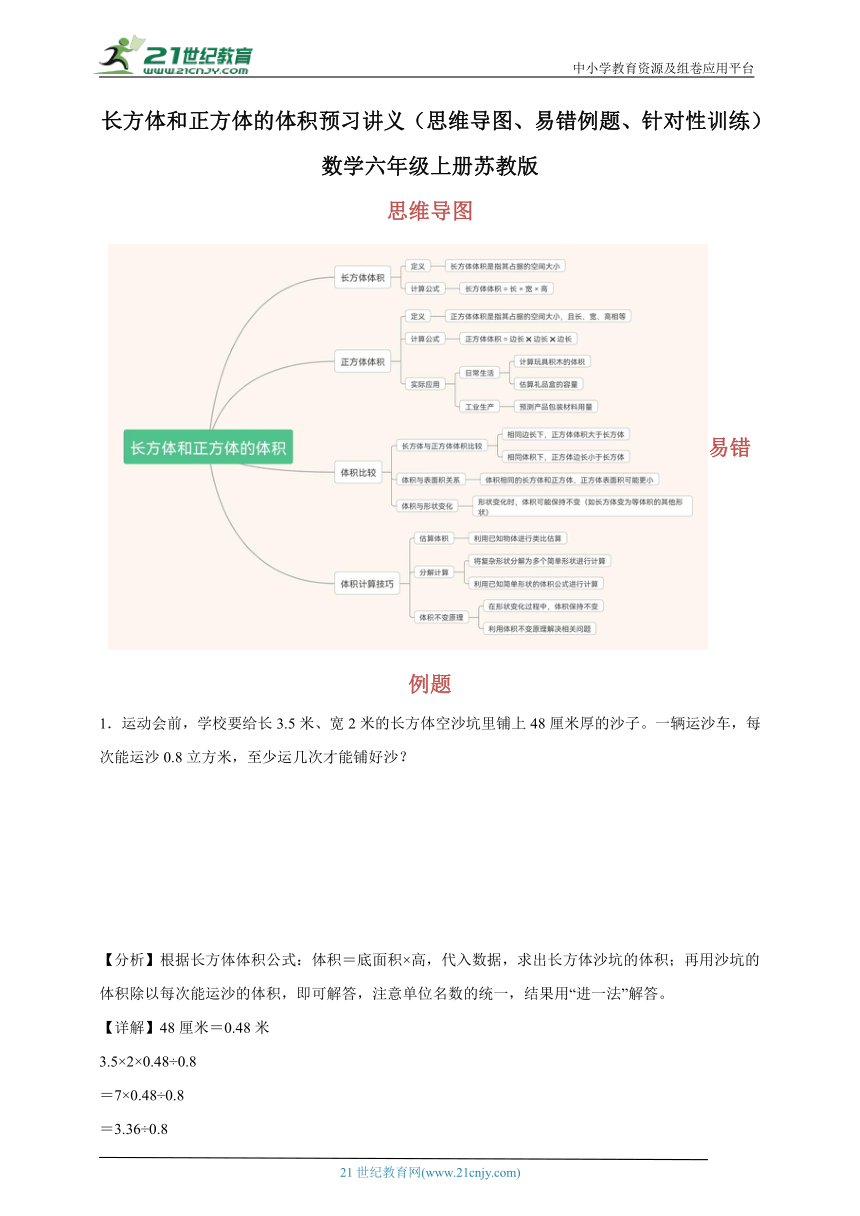
思维导图
易错例题
1.运动会前,学校要给长3.5米、宽2米的长方体空沙坑里铺上48厘米厚的沙子。一辆运沙车,每次能运沙0.8立方米,至少运几次才能铺好沙?
【分析】根据长方体体积公式:体积=底面积×高,代入数据,求出长方体沙坑的体积;再用沙坑的体积除以每次能运沙的体积,即可解答,注意单位名数的统一,结果用“进一法”解答。
【详解】48厘米=0.48米
3.5×2×0.48÷0.8
=7×0.48÷0.8
=3.36÷0.8
≈5(次)
答:至少运5次才能铺好沙。
2.张华用“排水法”测量1颗玻璃球的体积,下面是他的测量记录。
①选择一个正方体容器,从里面量,棱长是10厘米。
②往这个容器中倒入一些水,测得水面的高度是7厘米。
③把12颗完全相同的玻璃球轻轻地放入容器中,所有玻璃球都被水完全浸没。
④再次测得水面的高度是8.5厘米。
根据上面的测量记录,计算出1颗玻璃球的体积是多少立方厘米?
【分析】由题意可知原来水面的高度是7厘米,此时水的形状是一个长方体,体积就是10×10×7;将12颗完全相同的玻璃球放入容器后,水面升至8.5厘米,此时水的体积和玻璃球的体积和是10×10×8.5.再用现在的体积减去原来的体积,就能得到12颗玻璃球的体积和,因为玻璃球是完全相同的,最后用求得的差值除以12就能得到每个玻璃球的体积。
【详解】10×10×7=700(立方厘米)
10×10×8.5=850(立方厘米)
850-700=150(立方厘米)
150÷12=12.5(立方厘米)
答:1颗玻璃球的体积是12.5立方厘米。
【点睛】本题主要是要分析得出水面上升的体积就是放入小球的体积。
3.一张长方形硬纸板的面积是6平方分米,周长是10分米,水平摆放后向上平移,形成的长方体的表面积是36平方分米。这个长方体的体积是多少?
【分析】这是一道关于长方体的题目,根据长方形的周长、面积公式与长方体的表面积、体积公式解答; 由长方形的周长=(长+宽)×2可知,长+宽=周长÷2,据此可求出长方形长与宽的和,再结合长方形的面积=长×宽,可判断出长方形纸板的长与宽; 由长方体的表面积=(长×宽+长×高+宽×高)×2可得,长方体的高=(表面积÷2-长×宽)÷(长+宽),据此可求出长方体的高; 然后根据长方体的体积=长×宽×高,可求出这个长方体的体积。
【详解】10÷2=5(分米)
3+2=5(分米)
3×2=6(平方分米)
因此可知:长方形的长是3分米,宽是2分米。
长方体的高:
(36÷2-3×2)÷(3+2)
=(18-6)÷5
=12÷5
=2.4(分米)
长方体的体积:3×2×2.4
=6×2.4
=14.4(立方分米)
答:这个长方体的体积是14.4立方分米。
【点睛】利用长方体的表面积公式求出长方体的高是解题的关键。
4.一个长方体,若长增加4分米,宽和高都不变,则体积增加60立方分米;若宽减少3分米,长和高都不变,则体积减少72立方分米;若高增加2分米,长和宽都不变,则体积增加80立方分米。原来长方体的表面积是多少平方分米?
【分析】首先根据题意可知,如果长增加4分米,宽和高都不变,它的体积增加60立方分米,根据长方体的体积公式:长×宽×高,用原来的宽乘原来的高再乘增加部分的长就是增加部分的体积,可以求出:宽×高=60÷4=15(平方分米)
如果宽减小3分米,长和高都不变,它的体积减少72立方分米,可以求出:长×高=72÷3=24(平方分米)﹔
如果高增加2分米,长和宽都不变,它的体积增加80立方分米,可以求出长×宽=80÷2=40(平方分米);
然后根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据进行计算即可解决问题。
【详解】由分析可知:
宽×高:60÷4=15(平方分米)
长×高:72÷3=24(平方分米)
长×宽:80÷2=40(平方分米)
(15+24+40)×2
=(39+40)×2
=79×2
=158(平方分米)
针对性训练
一、选择题
1.一个长方体水箱最多能盛水20升,它的( )是20升。
A.体积 B.容积 C.表面积 D.底面积
2.一个从里面量长6dm、宽5dm、高4dm的长方体盒子,最多能放( )个棱长2dm的小正方体。
A.12 B.10 C.15 D.18
3.下面现实情境中最适合提出与“体积”有关的问题是( )。
A.给相框装上花边 B.给一块长方形菜地的四周围上篱笆
C.给学校的窗户安玻璃 D.给一个游泳池注水
4.一个长20厘米、宽9厘米、高3厘米的物体,最有可能是( )。
A.叠起来的10张作业纸 B.铅笔盒 C.数学书 D.橡皮
5.一个正方体的底面周长是12cm,它的体积是( )cm3。
A.9 B.27 C.36 D.48
6.把一个长6厘米,宽5厘米,高4厘米的长方体切成一个最大的正方体。这个正方体的体积是( )立方厘米。
A.216 B.132 C.125 D.64
7.一个长方体水缸,长20厘米,宽15厘米,将一块石头投入水中(石头全部浸没)水面上升2厘米,这块石头体积的计算算式是( )。
A. B.
C. D.
8.如图,一根长2m的长方体木料沿虚线锯成两段后,表面积增加100cm2,它的体积是( )。
A.200cm3 B.2cm3 C.10000cm3 D.1cm3
二、填空题
9.在括号里填上合适的单位名称。
(1)一块橡皮的体积大约是8( )。
(2)一个教室大约占地48( )。
(3)一盒纯牛奶是250( )。
(4)一种小汽车的油箱容积是40( )。
10.6立方米80立方分米=( )立方米 90秒=( )分
11.一个正方体的棱长总和是96厘米,这个正方体的表面积是( )平方厘米,体积是( )立方厘米。
12.一个长方体木块长21厘米,宽15厘米,高6厘米,体积是( )立方厘米;从这个木块上切下一个最大的正方体后,剩下部分的体积是( )立方厘米。
13.将一根60dm长的长方体木料平均锯成3段,表面积增加了80dm2,原来这根木料的体积是( )dm3。
14.把长7cm、宽5cm、高9cm的两个同样的长方体拼成一个更大的长方体,拼成的长方体的表面积最小是( )cm2,体积是( )cm3。
三、计算题
15.请你求下面正方体的表面积和体积。(单位:cm)
16.计算下边立体图形的表面积和体积。(单位:cm)
17.求下面图形的表面积和体积(单位:厘米)。
四、解答题
18.一根长12米的长方体木料,截成两段完全相同的长方体时,表面积增加了24平方分米,这根木料原来的体积是多少立方分米?
19.一个长方体水槽,从里面量得长15厘米、宽12厘米、高10厘米,水深7厘米。当把一块棱长6厘米的正方体石块完全浸没在水中后,水面上升到多少厘米?
20.把一个长8米、宽5米、高4.5米的水池中注满水,然后把两条长3米、宽2米、高4米的石柱浸没在水池中,水池溢出的水的体积是多少?
21.加工厂要加工一批洗衣机的机套(没有底面),每台洗衣机的长是50厘米,宽是40厘米,高70厘米。
(1)一台洗衣机的体积是多少立方分米?
(2)做100个洗衣机套至少要用布多少平方米?
参考答案:
1.B
【分析】容器所能容纳物体的体积,是容器的容积,据此解答即可。
【详解】一个长方体水箱最多能盛水20升,是将水箱看作一个容器,能容纳20升水的体积,所以是指水箱的容积是20升;
故答案为:B
2.A
【分析】分别用长方体的长、宽、高除以正方体的棱长,求出长方体的长、宽、高分别可以放多少个正方体,再相乘即可。
【详解】6÷2=3(个)
4÷2=2(个)
5÷2=2(个)……1(分米)
3×2×2=12(个)
故答案选:A
3.D
【分析】封闭图形一周的长度就是它的周长。物体表面或封闭图形的的大小就是它的面积。物体所占空间的大小就是它的体积。
【详解】A.给相框装上花边,花边的长度就是相框的周长;
B.给一块长方形菜地的四周围上篱笆,篱笆的长度指的是菜地的周长;
C.给学校的窗户安玻璃,指的是窗户的面积;
D.给一个游泳池注水,指的是水的体积。
故答案为:D
4.B
【分析】棱长1厘米的正方体,体积是1立方厘米,大约是1个手指头的大小,根据长方体体积=长×宽×高,求出这个物体的体积,再根据体积单位的认识,以及生活经验进行选择。
【详解】20×9×3=540(立方厘米)
A.叠起来的10张作业纸体积大约是2立方厘米;
B.铅笔盒的体积有可能是540立方厘米;
C.数学书的体积大约是200立方厘米;
D.橡皮的体积大约是6立方厘米;
最有可能是铅笔盒。
故答案为:B
5.B
【分析】根据正方形边长=周长÷4,求出正方体棱长,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】12÷4=3(cm)
3×3×3=27(cm3)
它的体积是27cm3。
故答案为:B
6.D
【分析】把一个长方体切成一个最大的正方体,正方体棱长=长方体最短的棱长,据此确定正方体棱长,根据正方体体积=棱长×棱长×棱长,列式计算即可。
【详解】把一个长6厘米,宽5厘米,高4厘米的长方体切成一个最大的正方体。这个正方体的棱长是4厘米。
4×4×4=64(立方厘米)
这个正方体的体积是64立方厘米。
故答案为:D
7.A
【分析】因为石头完全浸没在水中,所以石头的体积等于上升的水的体积,上升的水的体积等于长是20厘米,宽15厘米,高是2厘米的长方体的体积,根据长方体体积长×宽×高,计算即可。
【详解】20×15×2
=300×2
=600(立方厘米)
这块石头体积的计算算式是20×15×2。
故答案为:A
8.C
【分析】把一根长方体木料沿虚线锯成两段后,表面积比原来增加了2个横截面的面积,再根据长方体的体积公式:V=Sh,据此进行计算即可。
【详解】2m=200cm
100÷2=50(cm2)
50×200=10000(cm3)
则它的体积是10000cm3。
故答案为:C
9.(1)立方厘米/cm3
(2)平方米/m2
(3)毫升/mL
(4)升/L
【分析】根据面积单位、体积(容积)单位和数据大小的认识,结合实际生活;1立方厘米大约有大拇手指头的大小,所以一块橡皮用立方厘米比较合适;一个卧室的面积大约是15平方米,所以教室面积比卧室大一些,用平方米比较合适;1瓶矿泉水大约500毫升,1盒纯牛奶比1瓶矿泉水小,所以1盒纯牛奶用毫升比较合适;1桶食用油大约5升,1个油箱比食用油桶大的多,所以油箱容积用升比较合适。
【详解】(1)一块橡皮的体积大约是8立方厘米。
(2)一个教室大约占地48平方米。
(3)一盒纯牛奶是250毫升。
(4)一种小汽车的油箱容积是40升。
10. 6.08 1.5
【分析】根据进率:1立方米=1000立方分米,1分=60秒;从高级单位向低级单位转换,乘进率;从低级单位向高级单位转换,除以进率;据此解答。
【详解】(1)80÷1000=0.08(立方米)
6+0.08=6.08(立方米)
6立方米80立方分米=6.08立方米
(2)90÷60=1.5(分)
90秒=1.5分
11. 384 512
【分析】首先根据正方体的棱长总和=棱长×12,由此求出正方体的棱长,再根据正方体的表面积公式S=6a2,体积公式V=a3,把数据分别代入公式解答即可。
【详解】棱长:
正方体表面积:
(平方厘米)
正方体体积:
(立方厘米)
【点睛】本题考查正方体的棱长和、表面积、体积,解答本题的关键是掌握正方体的棱长和、表面积、体积计算公式。
12. 1890 1674
【分析】长方体体积=长×宽×高,据此求出木块体积;从长方体上切下一个最大的正方体,正方体的棱长等于长方体最短的一条棱,剩下部分的体积=长方体体积-正方体体积,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】21×15×6
=315×6
=1890(立方厘米)
6×6×6
=36×6
=216(立方厘米)
1890-216=1674(立方厘米)
它的体积是1890立方厘米,剩下部分的体积是1674立方厘米。
13.1200
【分析】长方体木料平均锯成3段,需要锯2次,每锯一次增加2个截面,增加的表面积÷增加的截面数量=横截面面积,根据长方体体积=横截面面积×长,列式计算即可。
【详解】2×(3-1)
=2×2
=4(个)
80÷4×60=1200(dm3)
原来这根木料的体积是1200dm3。
14. 446 630
【分析】要想拼成的表面积最小,要把最大的面重合在一起,即将7×9的面重合,拼成的长方体的长是7cm,宽是9cm,高是5+5=10(cm),再根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,将数据带入公式即可。
【详解】5+5=10(cm)
(7×10+9×10+7×9)×2
=(70+90+63)×2
=223×2
=446(cm2)
7×9×10=630(cm3)
则拼成的长方体的表面积最小是446cm2,体积是630cm3。
15.96平方厘米;64立方厘米
【分析】根据正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,列式计算即可。
【详解】4×4×6
=16×6
=96(平方厘米)
4×4×4
=16×4
=64(立方厘米)
它的表面积是96平方厘米,体积是64立方厘米。
16.150cm2;99cm3
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;
组合图形的表面积=长方体的表面积+正方体4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算求解。
组合图形的体积=长方体的体积+正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据计算求解。
【详解】表面积:
(8×3+8×3+3×3)×2+3×3×4
=(24+24+9)×2+9×4
=57×2+36
=114+36
=150(cm2)
体积:
8×3×3+3×3×3
=72+27
=99(cm3)
立体图形的表面积是150cm2,体积是99cm3。
17.2720平方厘米;8832立方厘米
【分析】在长方体的顶点处挖去一个小长方体,减少了3个面,又出现了同样的3个面,因此这个立体图形的表面积等于大长方体的表面积,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式计算;
这个立体图形的体积=大长方体体积-小长方体体积,长方体体积=长×宽×高,据此列式计算。
【详解】(24×20+24×20+20×20)×2
=(480+480+400)×2
=1360×2
=2720(平方厘米)
24×20×20-8×8×12
=9600-768
=8832(立方厘米)
这个立体图形的表面积是2720平方厘米,体积是8832立方厘米。
18.1440立方分米
【分析】根据题意,把长方体木料截成两段,要截1次,表面积会增加2个截面的面积;先用增加的表面积除以2,求出一个截面的面积;再根据长方体的体积公式V=Sh,求出这根木料原来的体积。注意单位的换算:1米=10分米。
【详解】12米=120分米
24÷2=12(平方分米)
12×120=1440(立方分米)
答:这个木料原来的体积是1440立方分米。
19.8.2厘米
【分析】石块的体积就是水面上升的体积,根据正方体体积=棱长×棱长×棱长,求出石块的体积,石块的体积÷长方体水槽底面积=水面上升的高度,加上原来水深即可。
【详解】6×6×6÷(15×12)+7
=216÷180+7
=1.2+7
=8.2(厘米)
答:水面上升到8.2厘米。
20.48立方米
【分析】根据题意,溢出水的体积就是石柱浸入水的体积,用石柱长×宽×高=溢出的水的体积,据此列式解答。
【详解】3×2×4×2
=6×4×2
=24×2
=48(立方米)
答:水池溢出的水的体积是48立方米。
21.(1)140立方分米
(2)146平方米
【分析】(1)根据所给数据,洗衣机是一个长方体,长方体体积=长×宽×高,代入数据求出洗衣机的体积,再根据1000立方厘米=1立方分米进行单位换算。
(2)1个洗衣机套所需要的布的面积是长方体5个面积的面积,即1个上底面和4个侧面的面积和,根据公式长方体的表面积(5个面)=长×宽+(长×高+宽×高)×2,代入数据求一个洗衣机套所用布的面积,再乘100,即可解答。注意根据10000平方厘米=1平方米进行单位换算。
【详解】(1)50×40×70=140000(立方厘米)=140(立方分米)
答:一台洗衣机的体积是140立方分米.
(2)[50×40+(40×70+50×70)×2]×100
=[2000+(2800+3500)×2]×100
=[2000+6300×2]×100
=[2000+12600]×100
=14600×100
=1460000(平方厘米)=146(平方米)
答:做100个洗衣机套至少要用布146平方米。
答:原来长方体的表面积是158平方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
长方体和正方体的体积预习讲义(思维导图、易错例题、针对性训练)数学六年级上册苏教版
思维导图
易错例题
1.运动会前,学校要给长3.5米、宽2米的长方体空沙坑里铺上48厘米厚的沙子。一辆运沙车,每次能运沙0.8立方米,至少运几次才能铺好沙?
【分析】根据长方体体积公式:体积=底面积×高,代入数据,求出长方体沙坑的体积;再用沙坑的体积除以每次能运沙的体积,即可解答,注意单位名数的统一,结果用“进一法”解答。
【详解】48厘米=0.48米
3.5×2×0.48÷0.8
=7×0.48÷0.8
=3.36÷0.8
≈5(次)
答:至少运5次才能铺好沙。
2.张华用“排水法”测量1颗玻璃球的体积,下面是他的测量记录。
①选择一个正方体容器,从里面量,棱长是10厘米。
②往这个容器中倒入一些水,测得水面的高度是7厘米。
③把12颗完全相同的玻璃球轻轻地放入容器中,所有玻璃球都被水完全浸没。
④再次测得水面的高度是8.5厘米。
根据上面的测量记录,计算出1颗玻璃球的体积是多少立方厘米?
【分析】由题意可知原来水面的高度是7厘米,此时水的形状是一个长方体,体积就是10×10×7;将12颗完全相同的玻璃球放入容器后,水面升至8.5厘米,此时水的体积和玻璃球的体积和是10×10×8.5.再用现在的体积减去原来的体积,就能得到12颗玻璃球的体积和,因为玻璃球是完全相同的,最后用求得的差值除以12就能得到每个玻璃球的体积。
【详解】10×10×7=700(立方厘米)
10×10×8.5=850(立方厘米)
850-700=150(立方厘米)
150÷12=12.5(立方厘米)
答:1颗玻璃球的体积是12.5立方厘米。
【点睛】本题主要是要分析得出水面上升的体积就是放入小球的体积。
3.一张长方形硬纸板的面积是6平方分米,周长是10分米,水平摆放后向上平移,形成的长方体的表面积是36平方分米。这个长方体的体积是多少?
【分析】这是一道关于长方体的题目,根据长方形的周长、面积公式与长方体的表面积、体积公式解答; 由长方形的周长=(长+宽)×2可知,长+宽=周长÷2,据此可求出长方形长与宽的和,再结合长方形的面积=长×宽,可判断出长方形纸板的长与宽; 由长方体的表面积=(长×宽+长×高+宽×高)×2可得,长方体的高=(表面积÷2-长×宽)÷(长+宽),据此可求出长方体的高; 然后根据长方体的体积=长×宽×高,可求出这个长方体的体积。
【详解】10÷2=5(分米)
3+2=5(分米)
3×2=6(平方分米)
因此可知:长方形的长是3分米,宽是2分米。
长方体的高:
(36÷2-3×2)÷(3+2)
=(18-6)÷5
=12÷5
=2.4(分米)
长方体的体积:3×2×2.4
=6×2.4
=14.4(立方分米)
答:这个长方体的体积是14.4立方分米。
【点睛】利用长方体的表面积公式求出长方体的高是解题的关键。
4.一个长方体,若长增加4分米,宽和高都不变,则体积增加60立方分米;若宽减少3分米,长和高都不变,则体积减少72立方分米;若高增加2分米,长和宽都不变,则体积增加80立方分米。原来长方体的表面积是多少平方分米?
【分析】首先根据题意可知,如果长增加4分米,宽和高都不变,它的体积增加60立方分米,根据长方体的体积公式:长×宽×高,用原来的宽乘原来的高再乘增加部分的长就是增加部分的体积,可以求出:宽×高=60÷4=15(平方分米)
如果宽减小3分米,长和高都不变,它的体积减少72立方分米,可以求出:长×高=72÷3=24(平方分米)﹔
如果高增加2分米,长和宽都不变,它的体积增加80立方分米,可以求出长×宽=80÷2=40(平方分米);
然后根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据进行计算即可解决问题。
【详解】由分析可知:
宽×高:60÷4=15(平方分米)
长×高:72÷3=24(平方分米)
长×宽:80÷2=40(平方分米)
(15+24+40)×2
=(39+40)×2
=79×2
=158(平方分米)
针对性训练
一、选择题
1.一个长方体水箱最多能盛水20升,它的( )是20升。
A.体积 B.容积 C.表面积 D.底面积
2.一个从里面量长6dm、宽5dm、高4dm的长方体盒子,最多能放( )个棱长2dm的小正方体。
A.12 B.10 C.15 D.18
3.下面现实情境中最适合提出与“体积”有关的问题是( )。
A.给相框装上花边 B.给一块长方形菜地的四周围上篱笆
C.给学校的窗户安玻璃 D.给一个游泳池注水
4.一个长20厘米、宽9厘米、高3厘米的物体,最有可能是( )。
A.叠起来的10张作业纸 B.铅笔盒 C.数学书 D.橡皮
5.一个正方体的底面周长是12cm,它的体积是( )cm3。
A.9 B.27 C.36 D.48
6.把一个长6厘米,宽5厘米,高4厘米的长方体切成一个最大的正方体。这个正方体的体积是( )立方厘米。
A.216 B.132 C.125 D.64
7.一个长方体水缸,长20厘米,宽15厘米,将一块石头投入水中(石头全部浸没)水面上升2厘米,这块石头体积的计算算式是( )。
A. B.
C. D.
8.如图,一根长2m的长方体木料沿虚线锯成两段后,表面积增加100cm2,它的体积是( )。
A.200cm3 B.2cm3 C.10000cm3 D.1cm3
二、填空题
9.在括号里填上合适的单位名称。
(1)一块橡皮的体积大约是8( )。
(2)一个教室大约占地48( )。
(3)一盒纯牛奶是250( )。
(4)一种小汽车的油箱容积是40( )。
10.6立方米80立方分米=( )立方米 90秒=( )分
11.一个正方体的棱长总和是96厘米,这个正方体的表面积是( )平方厘米,体积是( )立方厘米。
12.一个长方体木块长21厘米,宽15厘米,高6厘米,体积是( )立方厘米;从这个木块上切下一个最大的正方体后,剩下部分的体积是( )立方厘米。
13.将一根60dm长的长方体木料平均锯成3段,表面积增加了80dm2,原来这根木料的体积是( )dm3。
14.把长7cm、宽5cm、高9cm的两个同样的长方体拼成一个更大的长方体,拼成的长方体的表面积最小是( )cm2,体积是( )cm3。
三、计算题
15.请你求下面正方体的表面积和体积。(单位:cm)
16.计算下边立体图形的表面积和体积。(单位:cm)
17.求下面图形的表面积和体积(单位:厘米)。
四、解答题
18.一根长12米的长方体木料,截成两段完全相同的长方体时,表面积增加了24平方分米,这根木料原来的体积是多少立方分米?
19.一个长方体水槽,从里面量得长15厘米、宽12厘米、高10厘米,水深7厘米。当把一块棱长6厘米的正方体石块完全浸没在水中后,水面上升到多少厘米?
20.把一个长8米、宽5米、高4.5米的水池中注满水,然后把两条长3米、宽2米、高4米的石柱浸没在水池中,水池溢出的水的体积是多少?
21.加工厂要加工一批洗衣机的机套(没有底面),每台洗衣机的长是50厘米,宽是40厘米,高70厘米。
(1)一台洗衣机的体积是多少立方分米?
(2)做100个洗衣机套至少要用布多少平方米?
参考答案:
1.B
【分析】容器所能容纳物体的体积,是容器的容积,据此解答即可。
【详解】一个长方体水箱最多能盛水20升,是将水箱看作一个容器,能容纳20升水的体积,所以是指水箱的容积是20升;
故答案为:B
2.A
【分析】分别用长方体的长、宽、高除以正方体的棱长,求出长方体的长、宽、高分别可以放多少个正方体,再相乘即可。
【详解】6÷2=3(个)
4÷2=2(个)
5÷2=2(个)……1(分米)
3×2×2=12(个)
故答案选:A
3.D
【分析】封闭图形一周的长度就是它的周长。物体表面或封闭图形的的大小就是它的面积。物体所占空间的大小就是它的体积。
【详解】A.给相框装上花边,花边的长度就是相框的周长;
B.给一块长方形菜地的四周围上篱笆,篱笆的长度指的是菜地的周长;
C.给学校的窗户安玻璃,指的是窗户的面积;
D.给一个游泳池注水,指的是水的体积。
故答案为:D
4.B
【分析】棱长1厘米的正方体,体积是1立方厘米,大约是1个手指头的大小,根据长方体体积=长×宽×高,求出这个物体的体积,再根据体积单位的认识,以及生活经验进行选择。
【详解】20×9×3=540(立方厘米)
A.叠起来的10张作业纸体积大约是2立方厘米;
B.铅笔盒的体积有可能是540立方厘米;
C.数学书的体积大约是200立方厘米;
D.橡皮的体积大约是6立方厘米;
最有可能是铅笔盒。
故答案为:B
5.B
【分析】根据正方形边长=周长÷4,求出正方体棱长,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】12÷4=3(cm)
3×3×3=27(cm3)
它的体积是27cm3。
故答案为:B
6.D
【分析】把一个长方体切成一个最大的正方体,正方体棱长=长方体最短的棱长,据此确定正方体棱长,根据正方体体积=棱长×棱长×棱长,列式计算即可。
【详解】把一个长6厘米,宽5厘米,高4厘米的长方体切成一个最大的正方体。这个正方体的棱长是4厘米。
4×4×4=64(立方厘米)
这个正方体的体积是64立方厘米。
故答案为:D
7.A
【分析】因为石头完全浸没在水中,所以石头的体积等于上升的水的体积,上升的水的体积等于长是20厘米,宽15厘米,高是2厘米的长方体的体积,根据长方体体积长×宽×高,计算即可。
【详解】20×15×2
=300×2
=600(立方厘米)
这块石头体积的计算算式是20×15×2。
故答案为:A
8.C
【分析】把一根长方体木料沿虚线锯成两段后,表面积比原来增加了2个横截面的面积,再根据长方体的体积公式:V=Sh,据此进行计算即可。
【详解】2m=200cm
100÷2=50(cm2)
50×200=10000(cm3)
则它的体积是10000cm3。
故答案为:C
9.(1)立方厘米/cm3
(2)平方米/m2
(3)毫升/mL
(4)升/L
【分析】根据面积单位、体积(容积)单位和数据大小的认识,结合实际生活;1立方厘米大约有大拇手指头的大小,所以一块橡皮用立方厘米比较合适;一个卧室的面积大约是15平方米,所以教室面积比卧室大一些,用平方米比较合适;1瓶矿泉水大约500毫升,1盒纯牛奶比1瓶矿泉水小,所以1盒纯牛奶用毫升比较合适;1桶食用油大约5升,1个油箱比食用油桶大的多,所以油箱容积用升比较合适。
【详解】(1)一块橡皮的体积大约是8立方厘米。
(2)一个教室大约占地48平方米。
(3)一盒纯牛奶是250毫升。
(4)一种小汽车的油箱容积是40升。
10. 6.08 1.5
【分析】根据进率:1立方米=1000立方分米,1分=60秒;从高级单位向低级单位转换,乘进率;从低级单位向高级单位转换,除以进率;据此解答。
【详解】(1)80÷1000=0.08(立方米)
6+0.08=6.08(立方米)
6立方米80立方分米=6.08立方米
(2)90÷60=1.5(分)
90秒=1.5分
11. 384 512
【分析】首先根据正方体的棱长总和=棱长×12,由此求出正方体的棱长,再根据正方体的表面积公式S=6a2,体积公式V=a3,把数据分别代入公式解答即可。
【详解】棱长:
正方体表面积:
(平方厘米)
正方体体积:
(立方厘米)
【点睛】本题考查正方体的棱长和、表面积、体积,解答本题的关键是掌握正方体的棱长和、表面积、体积计算公式。
12. 1890 1674
【分析】长方体体积=长×宽×高,据此求出木块体积;从长方体上切下一个最大的正方体,正方体的棱长等于长方体最短的一条棱,剩下部分的体积=长方体体积-正方体体积,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】21×15×6
=315×6
=1890(立方厘米)
6×6×6
=36×6
=216(立方厘米)
1890-216=1674(立方厘米)
它的体积是1890立方厘米,剩下部分的体积是1674立方厘米。
13.1200
【分析】长方体木料平均锯成3段,需要锯2次,每锯一次增加2个截面,增加的表面积÷增加的截面数量=横截面面积,根据长方体体积=横截面面积×长,列式计算即可。
【详解】2×(3-1)
=2×2
=4(个)
80÷4×60=1200(dm3)
原来这根木料的体积是1200dm3。
14. 446 630
【分析】要想拼成的表面积最小,要把最大的面重合在一起,即将7×9的面重合,拼成的长方体的长是7cm,宽是9cm,高是5+5=10(cm),再根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,将数据带入公式即可。
【详解】5+5=10(cm)
(7×10+9×10+7×9)×2
=(70+90+63)×2
=223×2
=446(cm2)
7×9×10=630(cm3)
则拼成的长方体的表面积最小是446cm2,体积是630cm3。
15.96平方厘米;64立方厘米
【分析】根据正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,列式计算即可。
【详解】4×4×6
=16×6
=96(平方厘米)
4×4×4
=16×4
=64(立方厘米)
它的表面积是96平方厘米,体积是64立方厘米。
16.150cm2;99cm3
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;
组合图形的表面积=长方体的表面积+正方体4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算求解。
组合图形的体积=长方体的体积+正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据计算求解。
【详解】表面积:
(8×3+8×3+3×3)×2+3×3×4
=(24+24+9)×2+9×4
=57×2+36
=114+36
=150(cm2)
体积:
8×3×3+3×3×3
=72+27
=99(cm3)
立体图形的表面积是150cm2,体积是99cm3。
17.2720平方厘米;8832立方厘米
【分析】在长方体的顶点处挖去一个小长方体,减少了3个面,又出现了同样的3个面,因此这个立体图形的表面积等于大长方体的表面积,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式计算;
这个立体图形的体积=大长方体体积-小长方体体积,长方体体积=长×宽×高,据此列式计算。
【详解】(24×20+24×20+20×20)×2
=(480+480+400)×2
=1360×2
=2720(平方厘米)
24×20×20-8×8×12
=9600-768
=8832(立方厘米)
这个立体图形的表面积是2720平方厘米,体积是8832立方厘米。
18.1440立方分米
【分析】根据题意,把长方体木料截成两段,要截1次,表面积会增加2个截面的面积;先用增加的表面积除以2,求出一个截面的面积;再根据长方体的体积公式V=Sh,求出这根木料原来的体积。注意单位的换算:1米=10分米。
【详解】12米=120分米
24÷2=12(平方分米)
12×120=1440(立方分米)
答:这个木料原来的体积是1440立方分米。
19.8.2厘米
【分析】石块的体积就是水面上升的体积,根据正方体体积=棱长×棱长×棱长,求出石块的体积,石块的体积÷长方体水槽底面积=水面上升的高度,加上原来水深即可。
【详解】6×6×6÷(15×12)+7
=216÷180+7
=1.2+7
=8.2(厘米)
答:水面上升到8.2厘米。
20.48立方米
【分析】根据题意,溢出水的体积就是石柱浸入水的体积,用石柱长×宽×高=溢出的水的体积,据此列式解答。
【详解】3×2×4×2
=6×4×2
=24×2
=48(立方米)
答:水池溢出的水的体积是48立方米。
21.(1)140立方分米
(2)146平方米
【分析】(1)根据所给数据,洗衣机是一个长方体,长方体体积=长×宽×高,代入数据求出洗衣机的体积,再根据1000立方厘米=1立方分米进行单位换算。
(2)1个洗衣机套所需要的布的面积是长方体5个面积的面积,即1个上底面和4个侧面的面积和,根据公式长方体的表面积(5个面)=长×宽+(长×高+宽×高)×2,代入数据求一个洗衣机套所用布的面积,再乘100,即可解答。注意根据10000平方厘米=1平方米进行单位换算。
【详解】(1)50×40×70=140000(立方厘米)=140(立方分米)
答:一台洗衣机的体积是140立方分米.
(2)[50×40+(40×70+50×70)×2]×100
=[2000+(2800+3500)×2]×100
=[2000+6300×2]×100
=[2000+12600]×100
=14600×100
=1460000(平方厘米)=146(平方米)
答:做100个洗衣机套至少要用布146平方米。
答:原来长方体的表面积是158平方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
