小升初分班考易错点检测卷(试题)2023-2024学年数学六年级下册青岛版(含解析)
文档属性
| 名称 | 小升初分班考易错点检测卷(试题)2023-2024学年数学六年级下册青岛版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 667.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 19:48:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考易错点检测卷(试题)2023-2024学年数学六年级下册青岛版
一、选择题
1.下列各比,能与组成比例的是( )。
A. B.6∶5 C. D.5∶6
2.爸爸有2万元钱,有两种理财方式:一种是买3年期国债,年利率为4%;另一种是买银行1年期理财产品,年收益率是4%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大( )。
A.国债 B.理财产品 C.一样大 D.无法确定
3.同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,下列说法中不可能实现的是( )。
A.朝上的面点数之和为12 B.朝上的面点数之和小于3
C.朝上的面点数之和大于4且小于8 D.朝上的面点数之和为13
4.甲、乙、丙、丁四个商店同时促销一种原价为100元的花生油。甲商店按原价的85%出售;乙商店满200元一律降价25%出售;丙商店买四送一;丁商店第二桶打六折。妈妈要买2桶这样的花生油,想花钱最少,应该到( )商店去买。
A.甲 B.乙 C.丙 D.丁
5.有一列数:1,,,,,,,,,,,,,,,,…,则排列在第( )。
A.88个 B.94个 C.88个或94个 D.81个或88个
6.一个圆柱和一个圆锥的体积相等,高也相等。若圆柱的底面积是6.28平方厘米,则圆锥的底面积是( )平方厘米。
A.6.28 B.12.56 C.18.84 D.37.68
二、填空题
7.在括号填上合适的单位。
一间卧室的占地面积为30( );一瓶眼药水的容积是5( )。
8.三个连续自然数,中间的一个是N,其余两个分别是( )和( )。
9.在公路的一边种下21棵树(两端都种),每两棵之间的距离是4米,这条路长( )米。
10.一个正方体棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
11.一个最简真分数,它的分子、分母的乘积是12,这个分数是( )。
12.等底等高的圆柱和圆锥体积之差是24立方厘米,那么圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
13.如表中,若A与B成正比例,则“☆”代表的数是( ),若A与B成反比例,则“☆”代表的数是( )。
A 2 4
B 6 ☆
14.在一幅比例尺是1∶3000000的地图上量得甲、乙两地之间的距离是2厘米,甲、乙两地之间的实际距离是( )千米。
三、判断题
15.一个圆柱的高缩小到原来的,底面半径扩大到原来的3倍,它的体积不变。( )
16.点动成线,所以一只蚂蚁将距洞口20厘米处的食物拖回洞里所经过的路线一定是一条长为20厘米的线段。( )
17.在方格图中,数对(5,6)和(6,5)表示的是同一点。( )
18.正方形、长方形、圆和平行四边形都是轴对称图形。( )
19.在﹣5和﹣8之间,只有﹣6和﹣7两个负整数。( )
四、计算题
20.口算。
21.下列各题,怎样算简便就怎样算。
22.解方程。
23.计算下面图形的面积。
五、解答题
24.学校为了改善运动环境,修筑了一条塑胶跑道,实际造价21.6万元,比原计划的多0.6万元,原计划造价多少万元?(列方程解答)
25.如图是王大伯刚刚收获的圆锥形状的小麦堆,请问小麦堆的体积是多少立方米?(圆周率取3.14,得数用四舍五入法保留整数)
26.2022年6月5日10点44分,在酒泉卫星发射中心,神舟十四号载人飞船发射成功。飞船的某精密零件是按20∶1放大后画在图纸上的,量的这个零件在图纸上的长度为18厘米,则这个零件实际长多少毫米?
27.小张和小李是骑行爱好者,两人同时分别从两地骑车相向而行,小张每小时行驶20千米,小李的速度比小张慢10%,1.5小时后两人相遇。全程长多少千米?
28.修一条长150米的铁路,甲队单独修完需要15天,乙队单独修完需要30天。现在甲乙一起合修了全长的,问他们合修了多少天?
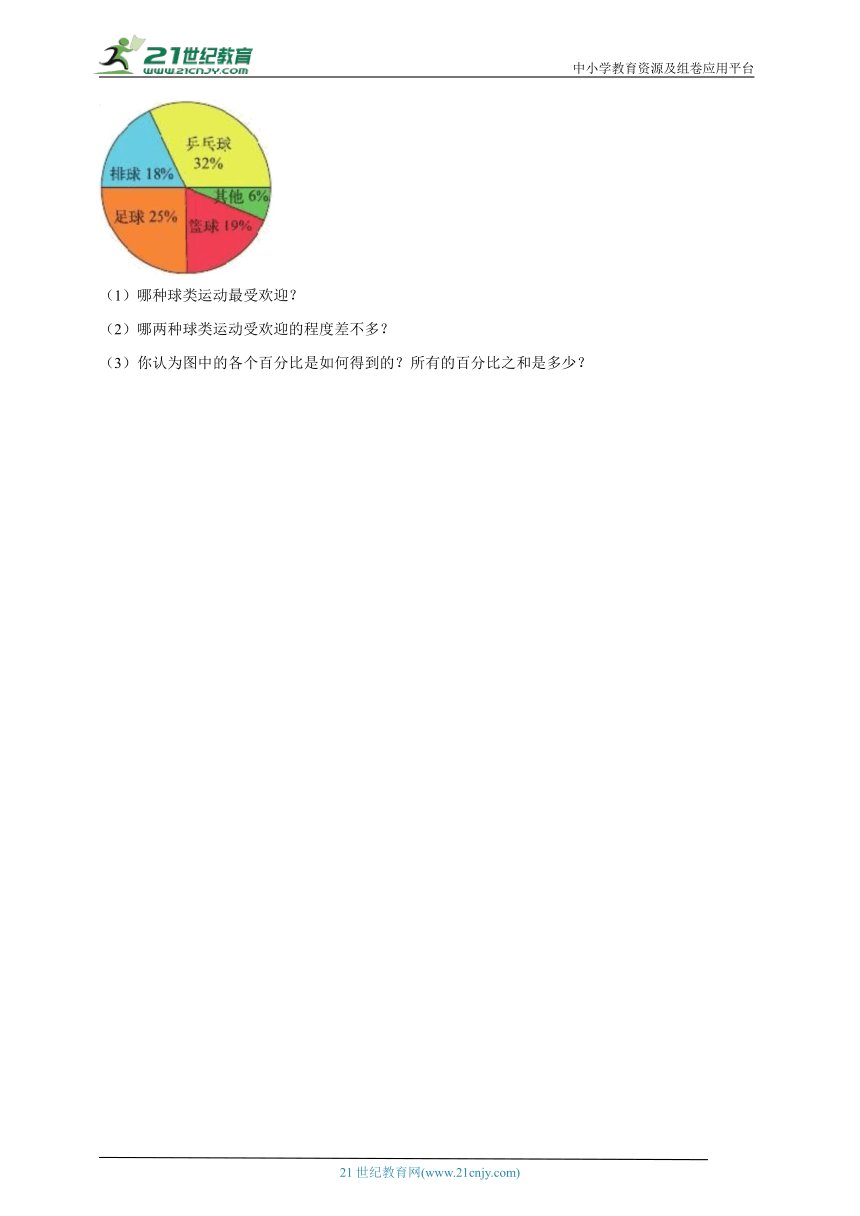
29.下图是某小学六年级学生关于“最受欢迎的球类运动”的统计图。
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎的程度差不多?
(3)你认为图中的各个百分比是如何得到的?所有的百分比之和是多少?
参考答案:
1.B
【分析】根据比例的意义,即表示两个比相等的式子叫做比例;判断两个比能否组成比例,就是看两个比的比值是否相等,若相等,则能组成比例,反之不能;先求出的比值,找出与它比值相等的式子即可。
【详解】=
A.=
B.6∶5=
C.=
D.5∶6=
故答案为:B
【点睛】此题考查的是比例的意义,解答此题的关键是明白:判断两个比能否组成比例,就是看两个比的比值是否相等,若相等,则能组成比例,反之不能。
2.B
【分析】先算出爸爸2万元买3年国债到期的利息,20000×4%×3=2400元,加上本金,20000+2400=22400元;爸爸买理财产品收益:第一年为:20000×4%=800元,本金+利息为:800+20000=20800元;第二年为:20800×4%=832元,本金+利息为:20800+832=21632元;第三年为:21632×4%=865.28元,本金+利息为:21632+865.28=22497.28元;比较22400和22497.28的大小,即可解答问题。
【详解】三年期:10000×4%×3
=400×3
=1200(元)
先买一年期,把本金和利息取出来合在一起,再存入一年,
10000×4%×1=400(元)
(10000+400)×4%×1
=10400×4%×1
=416(元)
(10000+400+416)×4%×1
=10816×4%×1
=432.64(元)
400+416+432.64
=816+432.64
=1248.64(元)
1200<1248.64
买银行1年期理财产品收益更大。
故答案为:B
【点睛】本题考查了利息相关问题,公式:利息=本金×利率×时间。
3.D
【分析】分别利用不可能事件和随机事件的定义分析得出即可。
【详解】因为同时抛掷两枚质地均匀的正方体骰子,正方体骰子的点数和应大于或等于2,而小于或等于12。显然,是不可能事件的是点数之和是13。
故答案为:D
【点睛】此题主要考查了随机事件和不可能事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.用到的知识点为:必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件。
4.B
【分析】根据题意,分别计算出妈妈在甲、乙、丙、丁四个商店买两桶油需要花的钱,进行比较一下即可知道,哪家商店便宜。
【详解】甲商店:
100×2×85%
=200×85%
=170(元)
乙商店:
100×2=200(元)
200×(1-25%)
=200×75%
=150(元)
丙商店:
100×2=200(元)
丁商店:
100+100×60%
=100+60
=160(元)
200>170>160>150
所以,乙商店最便宜。
故答案为:B
【点睛】正确理解“按原价的85%出售”、“满200元一律降价25%出售”、“买四送一”、“第二桶打六折”的意义,是解答此题的关键。
5.C
【分析】根据所给数可知,分母是1的有1个;分母是2的有3个;分母是3的有5个;分母是4的有7个……据此计算出分母是1-9的一共的个数,分母是10时,可能是第7个,也可能是第13个。据此计算即可。
【详解】1+3+5+7+9+11+13+15+17+7=88
1+3+5+7+9+11+13+15+17+13=94
据此可知排列在第88个或者第94个。
故答案为:C
【点睛】分析处数列的排列规律是解题关键。
6.C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,高也相等时,圆锥的底面积是圆柱底面积的3倍。据此解答即可。
【详解】6.28×3=18.84(平方厘米)
所以,圆锥的底面积是18.84平方厘米。
故答案为:C
【点睛】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
7. 平方米/m2 毫升/mL
【分析】边长1米的正方形,面积是1平方米,所以计量一间卧室的占地面积用“平方米”作单位比较合适;
1毫升液体的体积就是1立方厘米,计量比较少的液体,通常用“毫升”作单位,所以计量一瓶眼药水的容积用“毫升”作单位比较合适。
【详解】一间卧室的占地面积为30平方米;
一瓶眼药水的容积是5毫升。
8. N-1 N+1
【分析】根据三个连续自然数的特点可知,相邻两个自然数相差1;已知中间的一个是N,那么其余两个数分别比N少1和比N多1,据此解答。
【详解】三个连续自然数,中间的一个是N,其余两个分别是N-1和N+1。
9.80
【分析】根据植树问题中两端都栽的情况,间隔数=棵数-1;可知公路的一边种下21棵树,那么有(21-1)个间隔;再根据“间距×间隔数=全长”,求出这条路的全长。
【详解】4×(21-1)
=4×20
=80(米)
这条路长80米。
10. 4 8
【分析】根据正方体的表面积公式S=6a2以及积的变化规律可知,一个正方体棱长扩大到原来的2倍,则它的表面积扩大到原来的(2×2)倍;
根据正方体的体积公式V=a3以及积的变化规律可知,一个正方体棱长扩大到原来的2倍,则它的体积扩大到原来的(2×2×2)倍。
【详解】2×2=4
2×2×2=8
一个正方体棱长扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
11.或
【分析】根据题意,分子、分母的乘积是12,先看12是由哪两个数相乘得到,再把它们组成真分数,从中找出最简分数即可。
分子比分母小的分数叫做真分数;最简真分数是指分子和分母只有公因数1的真分数。
【详解】12=1×12=2×6=3×4
可以组成的真分数是:、、;
其中最简真分数是、;
所以,这个分数是或。
12. 36 12
【分析】根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍;可以把圆锥的体积看作1份,圆柱的体积看作3份,相差(3-1)份;
已知等底等高的圆柱和圆锥体积之差是24立方厘米,用体积之差除以份数差,即可求出一份数,也就是圆锥的体积;再用圆锥的体积乘3,求出圆柱的体积。
【详解】圆锥的体积:
24÷(3-1)
=24÷2
=12(立方厘米)
圆柱的体积:
12×3=36(立方厘米)
那么圆柱的体积是36立方厘米,圆锥的体积是12立方厘米。
13. 12 3
【分析】根据题意,若A和B成正比例,则2∶6=4∶☆,进而求出☆的值;若A和B成反比例,则2×6=4×☆,进而求出☆的值。
【详解】若A和B成正比例,
则2∶6=4∶☆
2☆=6×4
2☆=24
2☆÷2=24÷2
☆=12
若A和B成反比例,
则2×6=4×☆
12=4☆
4☆÷4=12÷4
☆=3
所以若A与B成正比例,则“☆”代表的数是12,若A与B成反比例,则“☆”代表的数是3。
14.60
【分析】已知一幅地图的比例尺和甲、乙两地的图上距离,根据“实际距离=图上距离÷比例尺”,以及进率“1千米=100000厘米”,求出甲、乙两地的实际距离。
【详解】2÷
=2×3000000
=6000000(厘米)
6000000厘米=60千米
甲、乙两地之间的实际距离是60千米。
15.×
【分析】根据圆柱的体积公式,假设原来圆柱的高为3,半径为1,高缩小到原来的后高为,底面半径扩大到原来的3倍后为,分别计算出变化前后圆柱的体积,再进行比较即可。
【详解】假设原来圆柱的高为3,半径为1,高缩小到原来的后高为,底面半径扩大到原来的3倍后为。
原来的体积:
变化后的体积:
所以一个圆柱的高缩小到原来的,底面半径扩大到原来的3倍,它的体积扩大到原来的3倍,原题说法错误。
故答案为:×
16.×
【分析】根据“两点之间线段最短”,但蚂蚁将距洞口20厘米处的食物拖回洞里,在拖动的过程中蚂蚁可能走的是曲线,所以所经过的路线不一定是一条长为20厘米的线段。
【详解】一只蚂蚁将距洞口20厘米处的食物拖回洞里所经过的路线不一定是一条长为20厘米的线段。
原题说法错误。
故答案为:×
17.×
【分析】用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
【详解】数对(5,6)表示第5列第6行,(6,5)表示第6列第5行,数对(5,6)和(6,5)表示的位置不同。
故答案为:×
18.×
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫作轴对称图形,这条直线就是其对称轴。
【详解】正方形、长方形、圆是轴对称图形,平行四边形不是轴对称图形。原题说法错误。
故答案为:×
19.√
【分析】比0大的数是正数,比0小的数是负数。0既不是正数,也不是负数。负数除了负整数,还有负小数、负分数, 据此判断。
【详解】根据分析可得:
﹣5和﹣8之间,有无数个负数,如﹣5.7,﹣6…,但负整数只有﹣6和﹣7两个。原说法正确。
故答案为:√
20.320;4.5;6.7;0.42;
2;3;;
【详解】略
21.8.5;11;
【分析】(1)运用乘法分配律进行计算即可;
(2)运用乘法分配律进行计算即可;
(3)先算括号里面的加法和减法,再算括号外面的乘法即可。
【详解】
=
=
=
=
=
=11
=
=
22.;;
【分析】先把20%化为小数0.2,再化简等号左边的算式,然后应用等式的性质2,方程左右两边同时除以0.7,得到方程的解;
根据比例的基本性质,把比例式转化为乘积式,再应用等式的性质2,方程左右两边同时除以0.4,得到方程的解;
根据比例的基本性质,把比例式转化为乘积式,再应用等式的性质2,方程左右两边同时除以,得到方程的解。
【详解】
解:0.5x+0.2x=8.4
0.7x=8.4
x=8.4÷0.7
x=12
解:0.4x=0.75×12
0.4x=9
x=9÷0.4
x=22.5
解:
23.4.43dm2
【分析】根据梯形的面积公式:S=(a+b)h÷2,半圆的面积公式:S=r2÷2,把数据代入公式求出梯形与半圆的面积,再用梯形的面积减去半圆的面积求差即可。
【详解】(2+4)×2÷2-3.14×(2÷2)2÷2
=6×2÷2-3.14×1÷2
=6-1.57
=4.43(dm2)
它的面积是4.43dm2。
24.30万元
【详解】根据题意可知等量关系:原计划造价×+0.6万元=实际造价,设原计划造价x万元,列方程计算即可。
【解答】解:设原计划造价x万元。
x+0.6=21.6
x=21.6-0.6
x=21
x=21÷
x=21×
x=30
答:原计划造价30万元。
【点睛】本题主要考查了分数除法的应用,关键是找等量关系再列方程解答。
25.33立方米
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式计算即可求出这堆小麦的体积。
【详解】8÷2=4(米)
3.14×42×2×
=3.14×16×2×
=100.48×
≈33(立方米)
答:小麦堆的体积是33立方米。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
26.9毫米
【分析】要求这个零件实际长多少厘米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【详解】18厘米=180毫米
180÷=9(毫米)
答:这个零件实际长9毫米。
【点睛】此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论,注意单位统一。
27.57千米
【分析】小李的速度比小张慢10%,则把小张的速度看作单位“1”,小李的速度是小张的(1-10%),根据百分数乘法的意义,用小张的速度乘(1-10%)即可求出小李的速度,再根据速度和×相遇时间=总路程解答即可。
【详解】20×(1-10%)
=20×0.9
=18(千米/时)
(20+18)×1.5
=38×1.5
=57(千米)
答:全程长57千米。
【点睛】本题考查了百分数的应用以及相遇问题,明确求比一个数多(少)百分之几的数是多少,用乘法计算。
28.2天
【分析】根据甲乙单独完成工作的时间,可以用分率(把总量看作单位“1”)表示出甲乙的工作效率,再用除以两人的工作效率之和即可。
【详解】甲:1÷15=
乙:1÷30=
=
=2(天)
答:他们合修了2天。
【点睛】本题考查了工作量、工作时间、工作效率的关系,熟练掌握三者的关系是解题的关键。
29.(1)乒乓球
(2)排球和篮球
(3)见详解
【分析】(1)比较各种球类运动的对应百分率,哪种球类运动的对应百分率最大,哪种球类运动最受欢迎;
(2)观察扇形统计图或比较比较各种球类运动的对应百分率,所占区域差不多大,或对应百分率较为接近的两种球类运动受欢迎的程度差不多;
(3)将总人数看作单位“1”,喜欢每种球类运动的人数÷总人数,即可求出各个百分比,所有的百分比之和是“1”。
【详解】(1)32%>25%>19%>18%>6%
答:乒乓球运动最受欢迎。
(2)排球和篮球所占区域差不多大,对应百分率较为接近。
答:排球和篮球运动受欢迎的程度差不多。
(3)喜欢乒乓球的人数÷总人数=喜欢乒乓球运动的对应百分率;
喜欢排球的人数÷总人数=喜欢排球运动的对应百分率;
喜欢足球的人数÷总人数=喜欢足球运动的对应百分率;
喜欢篮球的人数÷总人数=喜欢篮球运动的对应百分率;
喜欢其他的人数÷总人数=喜欢其他运动的对应百分率;
32%+25%+19%+18%+6%=1
所有的百分比之和是1。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考易错点检测卷(试题)2023-2024学年数学六年级下册青岛版
一、选择题
1.下列各比,能与组成比例的是( )。
A. B.6∶5 C. D.5∶6
2.爸爸有2万元钱,有两种理财方式:一种是买3年期国债,年利率为4%;另一种是买银行1年期理财产品,年收益率是4%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大( )。
A.国债 B.理财产品 C.一样大 D.无法确定
3.同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,下列说法中不可能实现的是( )。
A.朝上的面点数之和为12 B.朝上的面点数之和小于3
C.朝上的面点数之和大于4且小于8 D.朝上的面点数之和为13
4.甲、乙、丙、丁四个商店同时促销一种原价为100元的花生油。甲商店按原价的85%出售;乙商店满200元一律降价25%出售;丙商店买四送一;丁商店第二桶打六折。妈妈要买2桶这样的花生油,想花钱最少,应该到( )商店去买。
A.甲 B.乙 C.丙 D.丁
5.有一列数:1,,,,,,,,,,,,,,,,…,则排列在第( )。
A.88个 B.94个 C.88个或94个 D.81个或88个
6.一个圆柱和一个圆锥的体积相等,高也相等。若圆柱的底面积是6.28平方厘米,则圆锥的底面积是( )平方厘米。
A.6.28 B.12.56 C.18.84 D.37.68
二、填空题
7.在括号填上合适的单位。
一间卧室的占地面积为30( );一瓶眼药水的容积是5( )。
8.三个连续自然数,中间的一个是N,其余两个分别是( )和( )。
9.在公路的一边种下21棵树(两端都种),每两棵之间的距离是4米,这条路长( )米。
10.一个正方体棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
11.一个最简真分数,它的分子、分母的乘积是12,这个分数是( )。
12.等底等高的圆柱和圆锥体积之差是24立方厘米,那么圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
13.如表中,若A与B成正比例,则“☆”代表的数是( ),若A与B成反比例,则“☆”代表的数是( )。
A 2 4
B 6 ☆
14.在一幅比例尺是1∶3000000的地图上量得甲、乙两地之间的距离是2厘米,甲、乙两地之间的实际距离是( )千米。
三、判断题
15.一个圆柱的高缩小到原来的,底面半径扩大到原来的3倍,它的体积不变。( )
16.点动成线,所以一只蚂蚁将距洞口20厘米处的食物拖回洞里所经过的路线一定是一条长为20厘米的线段。( )
17.在方格图中,数对(5,6)和(6,5)表示的是同一点。( )
18.正方形、长方形、圆和平行四边形都是轴对称图形。( )
19.在﹣5和﹣8之间,只有﹣6和﹣7两个负整数。( )
四、计算题
20.口算。
21.下列各题,怎样算简便就怎样算。
22.解方程。
23.计算下面图形的面积。
五、解答题
24.学校为了改善运动环境,修筑了一条塑胶跑道,实际造价21.6万元,比原计划的多0.6万元,原计划造价多少万元?(列方程解答)
25.如图是王大伯刚刚收获的圆锥形状的小麦堆,请问小麦堆的体积是多少立方米?(圆周率取3.14,得数用四舍五入法保留整数)
26.2022年6月5日10点44分,在酒泉卫星发射中心,神舟十四号载人飞船发射成功。飞船的某精密零件是按20∶1放大后画在图纸上的,量的这个零件在图纸上的长度为18厘米,则这个零件实际长多少毫米?
27.小张和小李是骑行爱好者,两人同时分别从两地骑车相向而行,小张每小时行驶20千米,小李的速度比小张慢10%,1.5小时后两人相遇。全程长多少千米?
28.修一条长150米的铁路,甲队单独修完需要15天,乙队单独修完需要30天。现在甲乙一起合修了全长的,问他们合修了多少天?
29.下图是某小学六年级学生关于“最受欢迎的球类运动”的统计图。
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎的程度差不多?
(3)你认为图中的各个百分比是如何得到的?所有的百分比之和是多少?
参考答案:
1.B
【分析】根据比例的意义,即表示两个比相等的式子叫做比例;判断两个比能否组成比例,就是看两个比的比值是否相等,若相等,则能组成比例,反之不能;先求出的比值,找出与它比值相等的式子即可。
【详解】=
A.=
B.6∶5=
C.=
D.5∶6=
故答案为:B
【点睛】此题考查的是比例的意义,解答此题的关键是明白:判断两个比能否组成比例,就是看两个比的比值是否相等,若相等,则能组成比例,反之不能。
2.B
【分析】先算出爸爸2万元买3年国债到期的利息,20000×4%×3=2400元,加上本金,20000+2400=22400元;爸爸买理财产品收益:第一年为:20000×4%=800元,本金+利息为:800+20000=20800元;第二年为:20800×4%=832元,本金+利息为:20800+832=21632元;第三年为:21632×4%=865.28元,本金+利息为:21632+865.28=22497.28元;比较22400和22497.28的大小,即可解答问题。
【详解】三年期:10000×4%×3
=400×3
=1200(元)
先买一年期,把本金和利息取出来合在一起,再存入一年,
10000×4%×1=400(元)
(10000+400)×4%×1
=10400×4%×1
=416(元)
(10000+400+416)×4%×1
=10816×4%×1
=432.64(元)
400+416+432.64
=816+432.64
=1248.64(元)
1200<1248.64
买银行1年期理财产品收益更大。
故答案为:B
【点睛】本题考查了利息相关问题,公式:利息=本金×利率×时间。
3.D
【分析】分别利用不可能事件和随机事件的定义分析得出即可。
【详解】因为同时抛掷两枚质地均匀的正方体骰子,正方体骰子的点数和应大于或等于2,而小于或等于12。显然,是不可能事件的是点数之和是13。
故答案为:D
【点睛】此题主要考查了随机事件和不可能事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.用到的知识点为:必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件。
4.B
【分析】根据题意,分别计算出妈妈在甲、乙、丙、丁四个商店买两桶油需要花的钱,进行比较一下即可知道,哪家商店便宜。
【详解】甲商店:
100×2×85%
=200×85%
=170(元)
乙商店:
100×2=200(元)
200×(1-25%)
=200×75%
=150(元)
丙商店:
100×2=200(元)
丁商店:
100+100×60%
=100+60
=160(元)
200>170>160>150
所以,乙商店最便宜。
故答案为:B
【点睛】正确理解“按原价的85%出售”、“满200元一律降价25%出售”、“买四送一”、“第二桶打六折”的意义,是解答此题的关键。
5.C
【分析】根据所给数可知,分母是1的有1个;分母是2的有3个;分母是3的有5个;分母是4的有7个……据此计算出分母是1-9的一共的个数,分母是10时,可能是第7个,也可能是第13个。据此计算即可。
【详解】1+3+5+7+9+11+13+15+17+7=88
1+3+5+7+9+11+13+15+17+13=94
据此可知排列在第88个或者第94个。
故答案为:C
【点睛】分析处数列的排列规律是解题关键。
6.C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,高也相等时,圆锥的底面积是圆柱底面积的3倍。据此解答即可。
【详解】6.28×3=18.84(平方厘米)
所以,圆锥的底面积是18.84平方厘米。
故答案为:C
【点睛】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
7. 平方米/m2 毫升/mL
【分析】边长1米的正方形,面积是1平方米,所以计量一间卧室的占地面积用“平方米”作单位比较合适;
1毫升液体的体积就是1立方厘米,计量比较少的液体,通常用“毫升”作单位,所以计量一瓶眼药水的容积用“毫升”作单位比较合适。
【详解】一间卧室的占地面积为30平方米;
一瓶眼药水的容积是5毫升。
8. N-1 N+1
【分析】根据三个连续自然数的特点可知,相邻两个自然数相差1;已知中间的一个是N,那么其余两个数分别比N少1和比N多1,据此解答。
【详解】三个连续自然数,中间的一个是N,其余两个分别是N-1和N+1。
9.80
【分析】根据植树问题中两端都栽的情况,间隔数=棵数-1;可知公路的一边种下21棵树,那么有(21-1)个间隔;再根据“间距×间隔数=全长”,求出这条路的全长。
【详解】4×(21-1)
=4×20
=80(米)
这条路长80米。
10. 4 8
【分析】根据正方体的表面积公式S=6a2以及积的变化规律可知,一个正方体棱长扩大到原来的2倍,则它的表面积扩大到原来的(2×2)倍;
根据正方体的体积公式V=a3以及积的变化规律可知,一个正方体棱长扩大到原来的2倍,则它的体积扩大到原来的(2×2×2)倍。
【详解】2×2=4
2×2×2=8
一个正方体棱长扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
11.或
【分析】根据题意,分子、分母的乘积是12,先看12是由哪两个数相乘得到,再把它们组成真分数,从中找出最简分数即可。
分子比分母小的分数叫做真分数;最简真分数是指分子和分母只有公因数1的真分数。
【详解】12=1×12=2×6=3×4
可以组成的真分数是:、、;
其中最简真分数是、;
所以,这个分数是或。
12. 36 12
【分析】根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍;可以把圆锥的体积看作1份,圆柱的体积看作3份,相差(3-1)份;
已知等底等高的圆柱和圆锥体积之差是24立方厘米,用体积之差除以份数差,即可求出一份数,也就是圆锥的体积;再用圆锥的体积乘3,求出圆柱的体积。
【详解】圆锥的体积:
24÷(3-1)
=24÷2
=12(立方厘米)
圆柱的体积:
12×3=36(立方厘米)
那么圆柱的体积是36立方厘米,圆锥的体积是12立方厘米。
13. 12 3
【分析】根据题意,若A和B成正比例,则2∶6=4∶☆,进而求出☆的值;若A和B成反比例,则2×6=4×☆,进而求出☆的值。
【详解】若A和B成正比例,
则2∶6=4∶☆
2☆=6×4
2☆=24
2☆÷2=24÷2
☆=12
若A和B成反比例,
则2×6=4×☆
12=4☆
4☆÷4=12÷4
☆=3
所以若A与B成正比例,则“☆”代表的数是12,若A与B成反比例,则“☆”代表的数是3。
14.60
【分析】已知一幅地图的比例尺和甲、乙两地的图上距离,根据“实际距离=图上距离÷比例尺”,以及进率“1千米=100000厘米”,求出甲、乙两地的实际距离。
【详解】2÷
=2×3000000
=6000000(厘米)
6000000厘米=60千米
甲、乙两地之间的实际距离是60千米。
15.×
【分析】根据圆柱的体积公式,假设原来圆柱的高为3,半径为1,高缩小到原来的后高为,底面半径扩大到原来的3倍后为,分别计算出变化前后圆柱的体积,再进行比较即可。
【详解】假设原来圆柱的高为3,半径为1,高缩小到原来的后高为,底面半径扩大到原来的3倍后为。
原来的体积:
变化后的体积:
所以一个圆柱的高缩小到原来的,底面半径扩大到原来的3倍,它的体积扩大到原来的3倍,原题说法错误。
故答案为:×
16.×
【分析】根据“两点之间线段最短”,但蚂蚁将距洞口20厘米处的食物拖回洞里,在拖动的过程中蚂蚁可能走的是曲线,所以所经过的路线不一定是一条长为20厘米的线段。
【详解】一只蚂蚁将距洞口20厘米处的食物拖回洞里所经过的路线不一定是一条长为20厘米的线段。
原题说法错误。
故答案为:×
17.×
【分析】用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
【详解】数对(5,6)表示第5列第6行,(6,5)表示第6列第5行,数对(5,6)和(6,5)表示的位置不同。
故答案为:×
18.×
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫作轴对称图形,这条直线就是其对称轴。
【详解】正方形、长方形、圆是轴对称图形,平行四边形不是轴对称图形。原题说法错误。
故答案为:×
19.√
【分析】比0大的数是正数,比0小的数是负数。0既不是正数,也不是负数。负数除了负整数,还有负小数、负分数, 据此判断。
【详解】根据分析可得:
﹣5和﹣8之间,有无数个负数,如﹣5.7,﹣6…,但负整数只有﹣6和﹣7两个。原说法正确。
故答案为:√
20.320;4.5;6.7;0.42;
2;3;;
【详解】略
21.8.5;11;
【分析】(1)运用乘法分配律进行计算即可;
(2)运用乘法分配律进行计算即可;
(3)先算括号里面的加法和减法,再算括号外面的乘法即可。
【详解】
=
=
=
=
=
=11
=
=
22.;;
【分析】先把20%化为小数0.2,再化简等号左边的算式,然后应用等式的性质2,方程左右两边同时除以0.7,得到方程的解;
根据比例的基本性质,把比例式转化为乘积式,再应用等式的性质2,方程左右两边同时除以0.4,得到方程的解;
根据比例的基本性质,把比例式转化为乘积式,再应用等式的性质2,方程左右两边同时除以,得到方程的解。
【详解】
解:0.5x+0.2x=8.4
0.7x=8.4
x=8.4÷0.7
x=12
解:0.4x=0.75×12
0.4x=9
x=9÷0.4
x=22.5
解:
23.4.43dm2
【分析】根据梯形的面积公式:S=(a+b)h÷2,半圆的面积公式:S=r2÷2,把数据代入公式求出梯形与半圆的面积,再用梯形的面积减去半圆的面积求差即可。
【详解】(2+4)×2÷2-3.14×(2÷2)2÷2
=6×2÷2-3.14×1÷2
=6-1.57
=4.43(dm2)
它的面积是4.43dm2。
24.30万元
【详解】根据题意可知等量关系:原计划造价×+0.6万元=实际造价,设原计划造价x万元,列方程计算即可。
【解答】解:设原计划造价x万元。
x+0.6=21.6
x=21.6-0.6
x=21
x=21÷
x=21×
x=30
答:原计划造价30万元。
【点睛】本题主要考查了分数除法的应用,关键是找等量关系再列方程解答。
25.33立方米
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式计算即可求出这堆小麦的体积。
【详解】8÷2=4(米)
3.14×42×2×
=3.14×16×2×
=100.48×
≈33(立方米)
答:小麦堆的体积是33立方米。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
26.9毫米
【分析】要求这个零件实际长多少厘米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【详解】18厘米=180毫米
180÷=9(毫米)
答:这个零件实际长9毫米。
【点睛】此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论,注意单位统一。
27.57千米
【分析】小李的速度比小张慢10%,则把小张的速度看作单位“1”,小李的速度是小张的(1-10%),根据百分数乘法的意义,用小张的速度乘(1-10%)即可求出小李的速度,再根据速度和×相遇时间=总路程解答即可。
【详解】20×(1-10%)
=20×0.9
=18(千米/时)
(20+18)×1.5
=38×1.5
=57(千米)
答:全程长57千米。
【点睛】本题考查了百分数的应用以及相遇问题,明确求比一个数多(少)百分之几的数是多少,用乘法计算。
28.2天
【分析】根据甲乙单独完成工作的时间,可以用分率(把总量看作单位“1”)表示出甲乙的工作效率,再用除以两人的工作效率之和即可。
【详解】甲:1÷15=
乙:1÷30=
=
=2(天)
答:他们合修了2天。
【点睛】本题考查了工作量、工作时间、工作效率的关系,熟练掌握三者的关系是解题的关键。
29.(1)乒乓球
(2)排球和篮球
(3)见详解
【分析】(1)比较各种球类运动的对应百分率,哪种球类运动的对应百分率最大,哪种球类运动最受欢迎;
(2)观察扇形统计图或比较比较各种球类运动的对应百分率,所占区域差不多大,或对应百分率较为接近的两种球类运动受欢迎的程度差不多;
(3)将总人数看作单位“1”,喜欢每种球类运动的人数÷总人数,即可求出各个百分比,所有的百分比之和是“1”。
【详解】(1)32%>25%>19%>18%>6%
答:乒乓球运动最受欢迎。
(2)排球和篮球所占区域差不多大,对应百分率较为接近。
答:排球和篮球运动受欢迎的程度差不多。
(3)喜欢乒乓球的人数÷总人数=喜欢乒乓球运动的对应百分率;
喜欢排球的人数÷总人数=喜欢排球运动的对应百分率;
喜欢足球的人数÷总人数=喜欢足球运动的对应百分率;
喜欢篮球的人数÷总人数=喜欢篮球运动的对应百分率;
喜欢其他的人数÷总人数=喜欢其他运动的对应百分率;
32%+25%+19%+18%+6%=1
所有的百分比之和是1。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
