三角形的面积预习讲义(思维导图、易错例题、针对性训练)数学五年级上册苏教版
文档属性
| 名称 | 三角形的面积预习讲义(思维导图、易错例题、针对性训练)数学五年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 20:11:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
三角形的面积预习讲义(思维导图、易错例题、针对性训练)数学五年级上册苏教版
思维导图
易错例题
1.用两个完全一样的三角形能拼成一个底10厘米、高8厘米的平行四边形,每个三角形的面积是多少平方厘米?
【答案】40平方厘米
【分析】先根据平行四边形的面积=底×高,求出拼成的平行四边形的面积,也是这两个完全一样的三角形的面积之和;
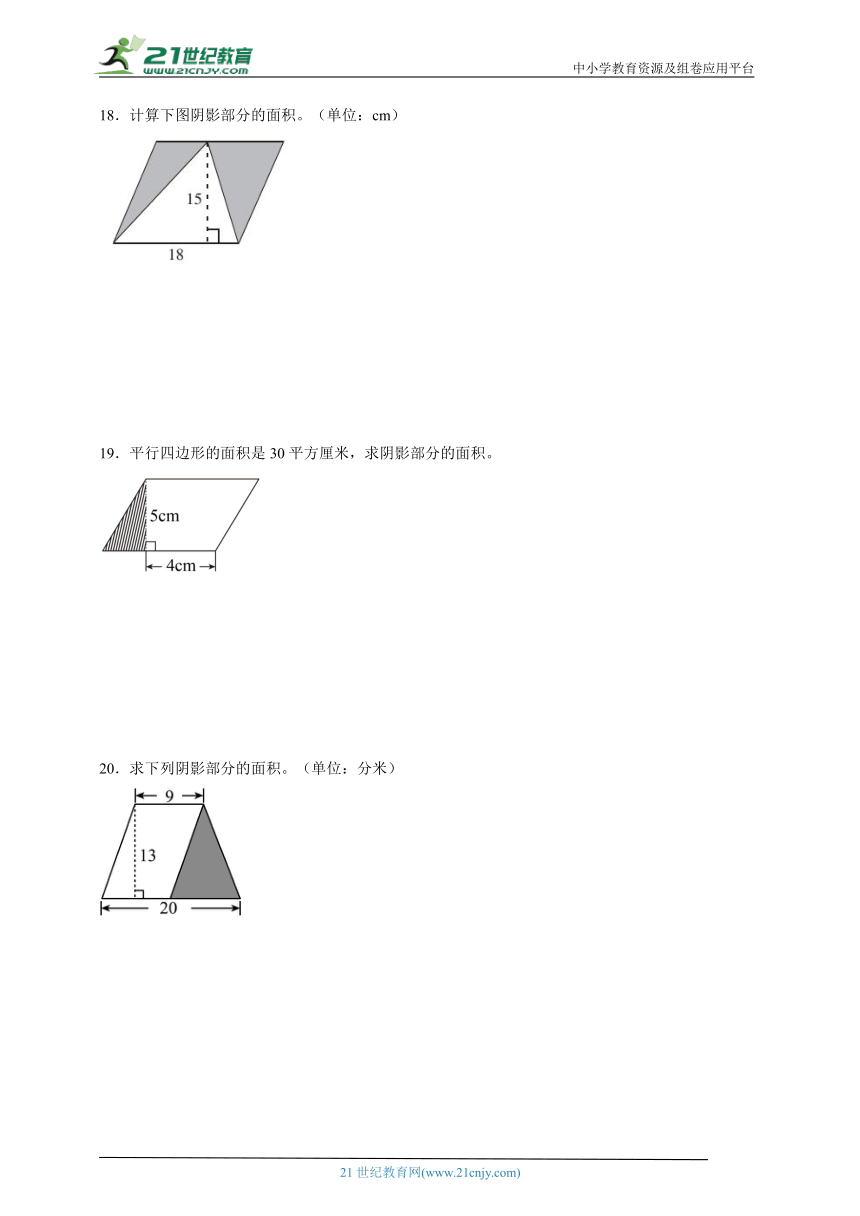
再用平行四边形的面积除以2,即可求出每个三角形的面积。
【详解】平行四边形的面积:10×8=80(平方厘米)
一个三角形的面积:80÷2=40(平方厘米)
答:每个三角形的面积是40平方厘米。
2.下图两个平行四边形的面积都是50平方厘米,两个涂色三角形的面积相等吗?为什么?
【答案】相等;理由见详解
【分析】已知两个平行四边形的面积都是50平方厘米,观察图形可知,两个涂色三角形与平行四边形等底等高,根据三角形的面积=底×高÷2,平行四边形的面积=底×高,可知三角形的面积是与它等底等高平行四边形面积的一半,据此解答。
【详解】50÷2=25(平方厘米)
答:两个涂色三角形的面积相等,都是25平方厘米。因为两个涂色三角形与平行四边形等底等高,所以两个涂色三角形的面积都等于平行四边形面积的一半。
3.一个梯形花坛,分成了一个平行四边形和一个三角形,分别种了郁金香和月季(如下图)。
这两种花的占地面积各是多少?
【答案】郁金香180平方米;月季54平方米
【分析】从图中可知,郁金香是一个底为15米、高为12米的平行四边形,根据平行四边形的面积=底×高,代入数据计算,即可求出郁金香的占地面积;
月季是一个底为(24-15)米,高为12米的三角形,根据三角形的面积=底×高÷2,代入数据计算,即可求出月季的占地面积。
【详解】郁金香的面积:
15×12=180(平方米)
月季的面积:
(24-15)×12÷2
=9×12÷2
=54(平方米)
答:郁金香的占地面积是180平方米,月季的占地面积是54平方米。
4.杨叔叔家有一块地。他把这块地分成一个平行四边形和三角形。平行四边形地里种黄瓜,三角形地里种西红柿。种西红柿的面积是36平方米。种黄瓜的面积是多少平方米?
【答案】96平方米
【分析】观察图形可知,平行四边形和三角形等高;已知三角形的面积是36平方米,底是6米,根据三角形的高=面积×2÷底,求出三角形的高,也就是平行四边形的高;又已知平行四边形的底是8米,根据平行四边形的面积=底×高,即可求出种黄瓜的面积。
【详解】三角形的高:
36×2÷6
=72÷6
=12(米)
平行四边形的面积:
8×12=96(平方米)
答:种黄瓜的面积是96平方米。
针对性训练
一、选择题
1.两个面积相等的三角形,形状( )。
A.不同 B.相同 C.有可能相同,也有可能不同
2.一个三角形的面积是40cm2,高是5cm,它的底是( )cm。
A.4 B.8 C.16
3.面积和底都相等的平行四边形和三角形,平行四边形的高是三角形高的( )。
A.4倍 B.2倍 C.一半
4.一个平行四边形和一个三角形等底等高,它们的面积之和是24平方厘米。三角形的面积是( )平方厘米。
A.12 B.8 C.4
5.直角三角形的三条边分别长6cm,8cm,10cm,这个三角形的面积是( )。
A. B. C.
6.如图,一组平行线所夹的两个阴影部分面积相比较。( )。
A.平行四边形面积大
B.面积一样大
C.三角形面积大
7.一个长方形的长是20cm,宽是15cm,在这个长方形内画一个最大的三角形,三角形的面积是( )。
A.150cm2 B.300cm2 C.75cm2
8.三角形的底和高都扩大到原来的2倍,则面积( )。
A.扩大到原来的2倍 B.扩大到原来的4倍 C.不变
二、填空题
9.下图中,平行四边形的面积是50平方厘米,三角形C的面积是( )平方厘米。
10.一个直角三角形的三条边分别是3厘米、4厘米和5厘米,这个直角三角形的面积是( )平方厘米。
11.如图,一块直角三角形的玻璃被打碎了,只剩下一部分,工人叔叔要照原样再切一块。这块玻璃的面积是( )cm2。
12.一个三角形的底是7分米,面积是63平方分米,高是( )分米。
三、判断题
13.一个三角形底边越小,面积就越小。( )
14.平行四边形的面积一定是三角形的面积的2倍。( )
15.若平行四边形与三角形等底等高,则它们的面积必定相等。( )
16.下图中两个涂色三角形的面积相等。( )
17.一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。( )
四、计算题
18.计算下图阴影部分的面积。(单位:cm)
19.平行四边形的面积是30平方厘米,求阴影部分的面积。
20.求下列阴影部分的面积。(单位:分米)
五、解答题
21.如下图,红领巾的底是98厘米,高是32厘米。红领巾的面积是多少平方厘米?
22.一块三角形棉花地底是120米,高是150米,如果每公顷地能产出棉花1500千克,这块地一共产出多少吨的棉花?
23.如图所示,完成下面的各题。
①用数对表示三角形B、C两个顶点的位置。
②画出三角形ABC关于直线的轴对称图形,并用阴影表示。
③画出将三角形ABC向右平移4格后的图形,并用阴影表示。
④如果图中每个小正方形的面积是1平方厘米,三角形ABC的面积是( )平方厘米。
24.如图,正方形的边长是12厘米,三角形甲的面积比三角形乙的面积大24平方厘米,线段长多少厘米?
25.一块三角形果园地,底30米,高16米。现在在这个果园里栽上梨树,已知每棵梨树的占地面积是4平方米,这块果园最多可以栽梨树多少棵?
26.一块三角形的地砖,它的底是36厘米,高是15厘米,它的面积是多少?
27.随着科学技术的发展进步,城市建设也融入了许多先进、智能的元素。郑州市地铁在部分站点设置了投影导向,能更加醒目地向大家传递信息。请根据图中的数据算一算,B出口的投影导向图的面积是多少?
28.小明和哥哥一起做了一个风筝,准备周末郊游时玩。
参考答案:
1.C
【分析】三角形的面积=底×高÷2,如果两个三角形的底与高的乘积相等,那么它们的面积就相等,与形状无关,据此分析解答。
【详解】由分析可知,两个面积相等的三角形,形状有可能相同,也有可能不同。
故答案为:C
2.C
【分析】根据三角形的面积=底×高÷2可得,三角形的底=三角形的面积×2÷高,据此代入数据解答即可。
【详解】40×2÷5
=80÷5
=16(cm)
它的底是16cm。
故答案为:C
3.C
【分析】设平行四边形和三角形的面积都为S,底为a。三角形面积=底×高÷2,三角形高=三角形面积×2÷底,即三角形高=S×2÷a=S÷a×2;平行四边面积=底×高,平行四边形高=平行四边面积÷底,即平行四边形高= S÷a。用平行四边形高÷平行四边形高即可求出它们的关系。
【详解】解:设平行四边形和三角形的面积都为S,底为a。
三角形的高=S×2÷a=S÷a×2
平行四边形的高= S÷a
S÷a÷(S÷a×2)
=(S÷a)÷(S÷a)÷2
=1÷2
=0.5
即,平行四边形的高是三角形高的一半。
故答案为:C
4.B
【分析】根据题意,结合平行四边形的面积公式:S=ah,三角形的面积公式:S=ah÷2可知,平行四边形的面积是与它等底等高的三角形面积的2倍,所以它们的面积和是三角形面积的3倍。据此解答。
【详解】24÷3=8(平方厘米)
三角形的面积是8平方厘米。
故答案为:B
5.A
【分析】因为直角三角形中,斜边最长,所以这个三角形的底和高分别是6cm和8cm,根据三角形面积公式:S=底×高÷2,将数据代入求解即可。
【详解】由分析可得:
6×8÷2
=48÷2
=24(cm2)
综上所述:直角三角形的三条边分别长6cm,8cm,10cm,这个三角形的面积是24cm2。
故答案为:A
【点睛】本题考查了三角形面积公式的灵活运用,解题的关键是牢记公式。
6.B
【分析】根据题意结合图形可知,平行四边形和三角形是等高的,所以设高为h,再根据三角形的面积公式:(底×高)÷2,平行四边形的面积公式:底×高,可以算出三角形的面积为8h÷2=4h,平行四边形的面积为4h。据此解答。
【详解】设高为h,所以三角形的面积为8h÷2=4h,平行四边形的面积为4h。
故答案为:B
【点睛】此题考查了三角形的面积公式以及平行四边形的面积公式。
7.A
【分析】长方形内画一个最大的三角形,三角形面积是长方形面积的一半,根据长方形面积=长×宽,求出长方形面积,除以2就是三角形面积。
【详解】20×15÷2
=300÷2
=150(cm2)
三角形的面积是150cm2。
故答案为:A
【点睛】关键是理解长方形和三角形之间的关系,掌握并灵活运用长方形面积公式。
8.B
【分析】假设三角形的底和高都是1,扩大到原来的2倍底和高都变成2,依据三角形的面积=底×高÷2,算出变化前后的面积做对比求解即可。
【详解】1×1÷2
=1÷2
=0.5
2×2÷2
=4÷2
=2
2÷0.5=4
三角形的面积扩大4倍。
故答案为:B
【点睛】熟练掌握三角形的面积公式是解题的关键。
9.25
【分析】观察图形可知,平行四边形和三角形C等底等高;根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知等底等高的三角形的面积是平行四边形面积的一半,据此解答。
【详解】50÷2=25(平方厘米)
三角形C的面积是25平方厘米。
10.6
【分析】直角三角形较短的两条边是直角边,两直角边可以看作底和高,根据三角形面积=底×高÷2,列式计算即可。
【详解】3×4÷2=6(平方厘米)
这个直角三角形的面积是6平方厘米。
11.18
【分析】根据三角形的内角和为180°可知,这个直角三角形的一个角是45°,另一个角是180°-90°-45°=45°,两个角相等,说明它是一个等腰直角三角形,则它的两条直角边相等,都是6cm。三角形的面积=底×高÷2,据此解答。
【详解】180°-90°-45°=45°
这个三角形是等腰直角三角形。
6×6÷2=18(cm2)
则这块玻璃的面积是18cm2。
12.18
【分析】根据三角形面积公式可得,三角形的高=面积×2÷底,据此列式计算。
【详解】63×2÷7=18(分米)
高是18分米。
13.×
【分析】根据三角形的面积=底×高÷2,可知三角形面积的大小与底边和对应的高有关。如果底边和高都变大或都变小,则三角形的面积一定变大或变小;如果只知道底边变小,不知道高是如何变化的,则三角形的面积不一定变小。
【详解】根据三角形的面积=底×高÷2,可知一个三角形底边越小,面积不一定变小。
原题说法错误。
故答案为:×
14.×
【分析】由三角形面积公式的推导过程可知,三角形的面积是与它等底等高的平行四边形面积的一半,而平行四边形的面积是与它等底等高三角形面积的2倍,据此解答。
【详解】由分析可知,平行四边形的面积是与它等底等高三角形面积的2倍,原题说法错误。
故答案为:×
15.×
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,据此解答。
【详解】根据平行四边形和三角形的面积公式,若平行四边形与三角形等底等高,则平行四边形的面积是三角形面积的2倍。原题说法错误。
故答案为:×
16.√
【分析】图中每个正方形大小相等,可以设正方形的边长是1厘米,然后根据三角形的面积=底×高÷2,分别求出两个涂色三角形的面积,再比较,得出结论。
【详解】设正方形的边长是1厘米。
上面涂色三角形的面积:1×1÷2=0.5(平方厘米)
下面涂色三角形的面积:1×1÷2=0.5(平方厘米)
0.5=0.5
所以,两个涂色三角形的面积相等。
原题说法正确。
故答案为:√
17.√
【分析】根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,求出高,再进行比较,即可解答。
【详解】16×2÷4
=32÷4
=8(cm)
一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。
原题干说法正确。
故答案为:√
18.135cm2
【分析】观察图形可知,阴影部分是两个等高的三角形,且它们的底相加等于18cm,所以它们的面积之和相当于一个底为18cm、高为15cm的三角形的面积;根据三角形的面积=底×高÷2,代入数据计算即可求出阴影部分的面积。
【详解】18×15÷2
=270÷2
=135(cm2)
阴影部分的面积是135cm2。
19.5平方厘米
【分析】根据平行四边形的面积公式:S=ah,即a=S÷h,据此求出平行四边形的底,进而求出阴影部分(三角形)的底,再根据三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】30÷5=6(厘米)
(6-4)×5÷2
=2×5÷2
=10÷2
=5(平方厘米)
则阴影部分的面积是5平方厘米。
20.71.5平方分米
【分析】由图可知,阴影部分的面积是底为(20-9)分米,高为13分米的三角形,根据三角形的面积=底×高÷2,代入数据进行解答即可。
【详解】(20-9)×13÷2
=11×13÷2
=143÷2
=71.5(平方分米)
阴影部分的面积是71.5平方分米。
21.1568平方厘米
【分析】红领巾是三角形。已知底是98厘米,高32厘米,应用三角形的面积公式就可求出红领巾的面积,即三角形的面积=底×高÷2。
【详解】98×32÷2
=3136÷2
=1568(平方厘米)
答:红领巾的面积是1568平方厘米。
22.1.35吨
【分析】根据三角形面积公式:面积=底×高÷2,代入数据,求出三角形棉花地的面积,1公顷=10000平方米,把面积单位化为公顷,再乘1500,求出能产出棉花的重量,1吨=1000千克,再化成吨,即可解答。
【详解】120×150÷2
=18000÷2
=9000(平方米)
9000平方米=0.9公顷
1500×0.9=1350(千克)
1350千克=1.35吨
答:这块地一共产出1.35吨的棉花。
23.①B(6,7);C(9,4)
②图见详解
③图见详解
④12
【分析】①数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,找出三角形B、C两个顶点在方格中对应的列数和行数,再用数对表示出来即可。
②补全轴对称图形的方法:找出三角形ABC三个顶点,依据对称轴画出三个顶点的对称点,再依据三角形ABC的形状顺次连接各点,画出最终的轴对称图形,并用阴影表示。
③根据平移的特征,把三角形ABC三个顶点分别先向右平移4格,再依次连接各顶点,即可得到平移后的三角形,并用阴影表示。
④从“每个小正方形的面积是1平方厘米”可知,小正方形的边长是1厘米,三角形ABC的底是8厘米,高是3厘米。根据三角形的面积底高,求出三角形ABC的面积即可。
【详解】①用数对表示三角形B、C两个顶点的位置。B(6,7);C(9,4)。
②、③根据要求作图如下:
④三角形ABC的面积:
8×3÷2
=24÷2
=12(平方厘米)
三角形ABC的面积是12平方厘米。
24.8厘米
【分析】如图,三角形甲的面积比三角形乙的面积大24平方厘米,甲+丙-24平方厘米=乙+丙,即正方形面积-24平方厘米=三角形BDE的面积,根据三角形的底=面积×2÷底,求出BD长,BD-CD=BC,据此列式解答。
【详解】12×12-24
=144-24
=120(平方厘米)
120×2÷12=20(厘米)
20-12=8(厘米)
答:线段长8厘米。
【点睛】关键是掌握并灵活运用正方形和三角形面积公式,根据三角形甲和三角形乙之间的关系,确定三角形BDE的面积。
25.60棵
【分析】根据三角形面积=底×高÷2,先求出果园面积,果园面积4每棵梨树占地面积=可以栽的梨树棵数,据此列式解答。
【详解】30×16÷2
=480÷2
=240(平方米)
240÷4=60(棵)
答:这块果园最多可以栽梨树60棵。
26.270平方厘米
【分析】根据三角形面积=底×高÷2,列式解答即可。
【详解】36×15÷2
=540÷2
=270(平方厘米)
答:它的面积是270平方厘米。
【点睛】关键是掌握并灵活运用三角形面积公式。
27.130平方分米
【分析】看图可知,投影导向图可以分成一个长方形加上一个三角形,根据长方形的面积公式:长×宽;三角形的面积公式:(底×高)÷2,两者面积加起来即可求出投影导向图的面积。
【详解】长方形的面积:10×9=90(平方分米)
三角形的面积:16×5÷2
=80÷2
=40(平方分米)
90+40=130(平方分米)
答:B出口的投影导向图的面积是130平方分米。
【点睛】此题考查了学生对三角形的面积公式以及长方形的面积公式的熟练掌握程度。
28.5张
【分析】根据三角形的面积=底×高÷2,用8×5÷2即可求出三角形的面积,再用三角形的面积除以一张纸的面积,即可求出需要的纸张数量。
【详解】8×5÷2÷4=5(张)
答:要用5张纸。
【点睛】本题主要考查了三角形面积公式的灵活应用,要熟练掌握相关公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
三角形的面积预习讲义(思维导图、易错例题、针对性训练)数学五年级上册苏教版
思维导图
易错例题
1.用两个完全一样的三角形能拼成一个底10厘米、高8厘米的平行四边形,每个三角形的面积是多少平方厘米?
【答案】40平方厘米
【分析】先根据平行四边形的面积=底×高,求出拼成的平行四边形的面积,也是这两个完全一样的三角形的面积之和;
再用平行四边形的面积除以2,即可求出每个三角形的面积。
【详解】平行四边形的面积:10×8=80(平方厘米)
一个三角形的面积:80÷2=40(平方厘米)
答:每个三角形的面积是40平方厘米。
2.下图两个平行四边形的面积都是50平方厘米,两个涂色三角形的面积相等吗?为什么?
【答案】相等;理由见详解
【分析】已知两个平行四边形的面积都是50平方厘米,观察图形可知,两个涂色三角形与平行四边形等底等高,根据三角形的面积=底×高÷2,平行四边形的面积=底×高,可知三角形的面积是与它等底等高平行四边形面积的一半,据此解答。
【详解】50÷2=25(平方厘米)
答:两个涂色三角形的面积相等,都是25平方厘米。因为两个涂色三角形与平行四边形等底等高,所以两个涂色三角形的面积都等于平行四边形面积的一半。
3.一个梯形花坛,分成了一个平行四边形和一个三角形,分别种了郁金香和月季(如下图)。
这两种花的占地面积各是多少?
【答案】郁金香180平方米;月季54平方米
【分析】从图中可知,郁金香是一个底为15米、高为12米的平行四边形,根据平行四边形的面积=底×高,代入数据计算,即可求出郁金香的占地面积;
月季是一个底为(24-15)米,高为12米的三角形,根据三角形的面积=底×高÷2,代入数据计算,即可求出月季的占地面积。
【详解】郁金香的面积:
15×12=180(平方米)
月季的面积:
(24-15)×12÷2
=9×12÷2
=54(平方米)
答:郁金香的占地面积是180平方米,月季的占地面积是54平方米。
4.杨叔叔家有一块地。他把这块地分成一个平行四边形和三角形。平行四边形地里种黄瓜,三角形地里种西红柿。种西红柿的面积是36平方米。种黄瓜的面积是多少平方米?
【答案】96平方米
【分析】观察图形可知,平行四边形和三角形等高;已知三角形的面积是36平方米,底是6米,根据三角形的高=面积×2÷底,求出三角形的高,也就是平行四边形的高;又已知平行四边形的底是8米,根据平行四边形的面积=底×高,即可求出种黄瓜的面积。
【详解】三角形的高:
36×2÷6
=72÷6
=12(米)
平行四边形的面积:
8×12=96(平方米)
答:种黄瓜的面积是96平方米。
针对性训练
一、选择题
1.两个面积相等的三角形,形状( )。
A.不同 B.相同 C.有可能相同,也有可能不同
2.一个三角形的面积是40cm2,高是5cm,它的底是( )cm。
A.4 B.8 C.16
3.面积和底都相等的平行四边形和三角形,平行四边形的高是三角形高的( )。
A.4倍 B.2倍 C.一半
4.一个平行四边形和一个三角形等底等高,它们的面积之和是24平方厘米。三角形的面积是( )平方厘米。
A.12 B.8 C.4
5.直角三角形的三条边分别长6cm,8cm,10cm,这个三角形的面积是( )。
A. B. C.
6.如图,一组平行线所夹的两个阴影部分面积相比较。( )。
A.平行四边形面积大
B.面积一样大
C.三角形面积大
7.一个长方形的长是20cm,宽是15cm,在这个长方形内画一个最大的三角形,三角形的面积是( )。
A.150cm2 B.300cm2 C.75cm2
8.三角形的底和高都扩大到原来的2倍,则面积( )。
A.扩大到原来的2倍 B.扩大到原来的4倍 C.不变
二、填空题
9.下图中,平行四边形的面积是50平方厘米,三角形C的面积是( )平方厘米。
10.一个直角三角形的三条边分别是3厘米、4厘米和5厘米,这个直角三角形的面积是( )平方厘米。
11.如图,一块直角三角形的玻璃被打碎了,只剩下一部分,工人叔叔要照原样再切一块。这块玻璃的面积是( )cm2。
12.一个三角形的底是7分米,面积是63平方分米,高是( )分米。
三、判断题
13.一个三角形底边越小,面积就越小。( )
14.平行四边形的面积一定是三角形的面积的2倍。( )
15.若平行四边形与三角形等底等高,则它们的面积必定相等。( )
16.下图中两个涂色三角形的面积相等。( )
17.一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。( )
四、计算题
18.计算下图阴影部分的面积。(单位:cm)
19.平行四边形的面积是30平方厘米,求阴影部分的面积。
20.求下列阴影部分的面积。(单位:分米)
五、解答题
21.如下图,红领巾的底是98厘米,高是32厘米。红领巾的面积是多少平方厘米?
22.一块三角形棉花地底是120米,高是150米,如果每公顷地能产出棉花1500千克,这块地一共产出多少吨的棉花?
23.如图所示,完成下面的各题。
①用数对表示三角形B、C两个顶点的位置。
②画出三角形ABC关于直线的轴对称图形,并用阴影表示。
③画出将三角形ABC向右平移4格后的图形,并用阴影表示。
④如果图中每个小正方形的面积是1平方厘米,三角形ABC的面积是( )平方厘米。
24.如图,正方形的边长是12厘米,三角形甲的面积比三角形乙的面积大24平方厘米,线段长多少厘米?
25.一块三角形果园地,底30米,高16米。现在在这个果园里栽上梨树,已知每棵梨树的占地面积是4平方米,这块果园最多可以栽梨树多少棵?
26.一块三角形的地砖,它的底是36厘米,高是15厘米,它的面积是多少?
27.随着科学技术的发展进步,城市建设也融入了许多先进、智能的元素。郑州市地铁在部分站点设置了投影导向,能更加醒目地向大家传递信息。请根据图中的数据算一算,B出口的投影导向图的面积是多少?
28.小明和哥哥一起做了一个风筝,准备周末郊游时玩。
参考答案:
1.C
【分析】三角形的面积=底×高÷2,如果两个三角形的底与高的乘积相等,那么它们的面积就相等,与形状无关,据此分析解答。
【详解】由分析可知,两个面积相等的三角形,形状有可能相同,也有可能不同。
故答案为:C
2.C
【分析】根据三角形的面积=底×高÷2可得,三角形的底=三角形的面积×2÷高,据此代入数据解答即可。
【详解】40×2÷5
=80÷5
=16(cm)
它的底是16cm。
故答案为:C
3.C
【分析】设平行四边形和三角形的面积都为S,底为a。三角形面积=底×高÷2,三角形高=三角形面积×2÷底,即三角形高=S×2÷a=S÷a×2;平行四边面积=底×高,平行四边形高=平行四边面积÷底,即平行四边形高= S÷a。用平行四边形高÷平行四边形高即可求出它们的关系。
【详解】解:设平行四边形和三角形的面积都为S,底为a。
三角形的高=S×2÷a=S÷a×2
平行四边形的高= S÷a
S÷a÷(S÷a×2)
=(S÷a)÷(S÷a)÷2
=1÷2
=0.5
即,平行四边形的高是三角形高的一半。
故答案为:C
4.B
【分析】根据题意,结合平行四边形的面积公式:S=ah,三角形的面积公式:S=ah÷2可知,平行四边形的面积是与它等底等高的三角形面积的2倍,所以它们的面积和是三角形面积的3倍。据此解答。
【详解】24÷3=8(平方厘米)
三角形的面积是8平方厘米。
故答案为:B
5.A
【分析】因为直角三角形中,斜边最长,所以这个三角形的底和高分别是6cm和8cm,根据三角形面积公式:S=底×高÷2,将数据代入求解即可。
【详解】由分析可得:
6×8÷2
=48÷2
=24(cm2)
综上所述:直角三角形的三条边分别长6cm,8cm,10cm,这个三角形的面积是24cm2。
故答案为:A
【点睛】本题考查了三角形面积公式的灵活运用,解题的关键是牢记公式。
6.B
【分析】根据题意结合图形可知,平行四边形和三角形是等高的,所以设高为h,再根据三角形的面积公式:(底×高)÷2,平行四边形的面积公式:底×高,可以算出三角形的面积为8h÷2=4h,平行四边形的面积为4h。据此解答。
【详解】设高为h,所以三角形的面积为8h÷2=4h,平行四边形的面积为4h。
故答案为:B
【点睛】此题考查了三角形的面积公式以及平行四边形的面积公式。
7.A
【分析】长方形内画一个最大的三角形,三角形面积是长方形面积的一半,根据长方形面积=长×宽,求出长方形面积,除以2就是三角形面积。
【详解】20×15÷2
=300÷2
=150(cm2)
三角形的面积是150cm2。
故答案为:A
【点睛】关键是理解长方形和三角形之间的关系,掌握并灵活运用长方形面积公式。
8.B
【分析】假设三角形的底和高都是1,扩大到原来的2倍底和高都变成2,依据三角形的面积=底×高÷2,算出变化前后的面积做对比求解即可。
【详解】1×1÷2
=1÷2
=0.5
2×2÷2
=4÷2
=2
2÷0.5=4
三角形的面积扩大4倍。
故答案为:B
【点睛】熟练掌握三角形的面积公式是解题的关键。
9.25
【分析】观察图形可知,平行四边形和三角形C等底等高;根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知等底等高的三角形的面积是平行四边形面积的一半,据此解答。
【详解】50÷2=25(平方厘米)
三角形C的面积是25平方厘米。
10.6
【分析】直角三角形较短的两条边是直角边,两直角边可以看作底和高,根据三角形面积=底×高÷2,列式计算即可。
【详解】3×4÷2=6(平方厘米)
这个直角三角形的面积是6平方厘米。
11.18
【分析】根据三角形的内角和为180°可知,这个直角三角形的一个角是45°,另一个角是180°-90°-45°=45°,两个角相等,说明它是一个等腰直角三角形,则它的两条直角边相等,都是6cm。三角形的面积=底×高÷2,据此解答。
【详解】180°-90°-45°=45°
这个三角形是等腰直角三角形。
6×6÷2=18(cm2)
则这块玻璃的面积是18cm2。
12.18
【分析】根据三角形面积公式可得,三角形的高=面积×2÷底,据此列式计算。
【详解】63×2÷7=18(分米)
高是18分米。
13.×
【分析】根据三角形的面积=底×高÷2,可知三角形面积的大小与底边和对应的高有关。如果底边和高都变大或都变小,则三角形的面积一定变大或变小;如果只知道底边变小,不知道高是如何变化的,则三角形的面积不一定变小。
【详解】根据三角形的面积=底×高÷2,可知一个三角形底边越小,面积不一定变小。
原题说法错误。
故答案为:×
14.×
【分析】由三角形面积公式的推导过程可知,三角形的面积是与它等底等高的平行四边形面积的一半,而平行四边形的面积是与它等底等高三角形面积的2倍,据此解答。
【详解】由分析可知,平行四边形的面积是与它等底等高三角形面积的2倍,原题说法错误。
故答案为:×
15.×
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,据此解答。
【详解】根据平行四边形和三角形的面积公式,若平行四边形与三角形等底等高,则平行四边形的面积是三角形面积的2倍。原题说法错误。
故答案为:×
16.√
【分析】图中每个正方形大小相等,可以设正方形的边长是1厘米,然后根据三角形的面积=底×高÷2,分别求出两个涂色三角形的面积,再比较,得出结论。
【详解】设正方形的边长是1厘米。
上面涂色三角形的面积:1×1÷2=0.5(平方厘米)
下面涂色三角形的面积:1×1÷2=0.5(平方厘米)
0.5=0.5
所以,两个涂色三角形的面积相等。
原题说法正确。
故答案为:√
17.√
【分析】根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,求出高,再进行比较,即可解答。
【详解】16×2÷4
=32÷4
=8(cm)
一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。
原题干说法正确。
故答案为:√
18.135cm2
【分析】观察图形可知,阴影部分是两个等高的三角形,且它们的底相加等于18cm,所以它们的面积之和相当于一个底为18cm、高为15cm的三角形的面积;根据三角形的面积=底×高÷2,代入数据计算即可求出阴影部分的面积。
【详解】18×15÷2
=270÷2
=135(cm2)
阴影部分的面积是135cm2。
19.5平方厘米
【分析】根据平行四边形的面积公式:S=ah,即a=S÷h,据此求出平行四边形的底,进而求出阴影部分(三角形)的底,再根据三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】30÷5=6(厘米)
(6-4)×5÷2
=2×5÷2
=10÷2
=5(平方厘米)
则阴影部分的面积是5平方厘米。
20.71.5平方分米
【分析】由图可知,阴影部分的面积是底为(20-9)分米,高为13分米的三角形,根据三角形的面积=底×高÷2,代入数据进行解答即可。
【详解】(20-9)×13÷2
=11×13÷2
=143÷2
=71.5(平方分米)
阴影部分的面积是71.5平方分米。
21.1568平方厘米
【分析】红领巾是三角形。已知底是98厘米,高32厘米,应用三角形的面积公式就可求出红领巾的面积,即三角形的面积=底×高÷2。
【详解】98×32÷2
=3136÷2
=1568(平方厘米)
答:红领巾的面积是1568平方厘米。
22.1.35吨
【分析】根据三角形面积公式:面积=底×高÷2,代入数据,求出三角形棉花地的面积,1公顷=10000平方米,把面积单位化为公顷,再乘1500,求出能产出棉花的重量,1吨=1000千克,再化成吨,即可解答。
【详解】120×150÷2
=18000÷2
=9000(平方米)
9000平方米=0.9公顷
1500×0.9=1350(千克)
1350千克=1.35吨
答:这块地一共产出1.35吨的棉花。
23.①B(6,7);C(9,4)
②图见详解
③图见详解
④12
【分析】①数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,找出三角形B、C两个顶点在方格中对应的列数和行数,再用数对表示出来即可。
②补全轴对称图形的方法:找出三角形ABC三个顶点,依据对称轴画出三个顶点的对称点,再依据三角形ABC的形状顺次连接各点,画出最终的轴对称图形,并用阴影表示。
③根据平移的特征,把三角形ABC三个顶点分别先向右平移4格,再依次连接各顶点,即可得到平移后的三角形,并用阴影表示。
④从“每个小正方形的面积是1平方厘米”可知,小正方形的边长是1厘米,三角形ABC的底是8厘米,高是3厘米。根据三角形的面积底高,求出三角形ABC的面积即可。
【详解】①用数对表示三角形B、C两个顶点的位置。B(6,7);C(9,4)。
②、③根据要求作图如下:
④三角形ABC的面积:
8×3÷2
=24÷2
=12(平方厘米)
三角形ABC的面积是12平方厘米。
24.8厘米
【分析】如图,三角形甲的面积比三角形乙的面积大24平方厘米,甲+丙-24平方厘米=乙+丙,即正方形面积-24平方厘米=三角形BDE的面积,根据三角形的底=面积×2÷底,求出BD长,BD-CD=BC,据此列式解答。
【详解】12×12-24
=144-24
=120(平方厘米)
120×2÷12=20(厘米)
20-12=8(厘米)
答:线段长8厘米。
【点睛】关键是掌握并灵活运用正方形和三角形面积公式,根据三角形甲和三角形乙之间的关系,确定三角形BDE的面积。
25.60棵
【分析】根据三角形面积=底×高÷2,先求出果园面积,果园面积4每棵梨树占地面积=可以栽的梨树棵数,据此列式解答。
【详解】30×16÷2
=480÷2
=240(平方米)
240÷4=60(棵)
答:这块果园最多可以栽梨树60棵。
26.270平方厘米
【分析】根据三角形面积=底×高÷2,列式解答即可。
【详解】36×15÷2
=540÷2
=270(平方厘米)
答:它的面积是270平方厘米。
【点睛】关键是掌握并灵活运用三角形面积公式。
27.130平方分米
【分析】看图可知,投影导向图可以分成一个长方形加上一个三角形,根据长方形的面积公式:长×宽;三角形的面积公式:(底×高)÷2,两者面积加起来即可求出投影导向图的面积。
【详解】长方形的面积:10×9=90(平方分米)
三角形的面积:16×5÷2
=80÷2
=40(平方分米)
90+40=130(平方分米)
答:B出口的投影导向图的面积是130平方分米。
【点睛】此题考查了学生对三角形的面积公式以及长方形的面积公式的熟练掌握程度。
28.5张
【分析】根据三角形的面积=底×高÷2,用8×5÷2即可求出三角形的面积,再用三角形的面积除以一张纸的面积,即可求出需要的纸张数量。
【详解】8×5÷2÷4=5(张)
答:要用5张纸。
【点睛】本题主要考查了三角形面积公式的灵活应用,要熟练掌握相关公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
