6.2.1 向量的加法运算 教学设计
文档属性
| 名称 | 6.2.1 向量的加法运算 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 00:00:00 | ||
图片预览

文档简介
人教版必修二 6.2.1向量的加法运算
教学内容分析
地位与作用
本节课选自人教A版必修第二册第六章“平面向量”第二节“平面向量的线性运算”第一课时.向量既有代数意义又有几何意义,作为沟通代数几何三角的桥梁,蕴含了数形结合、类比、归纳等数学思想方法,是培养学生数学抽象、逻辑推理、数学运算、直观想象等数学学科核心素养的极好载体.本单元将会从代数几何两方面对运算对象进行扩展,首先学习平面向量的加法运算,接着就是减法运算和数乘运算,平面向量的数量积,平面向量投影和投影向量,会利用向量运算判断两个向量的平行与垂直、求两个向量的夹角.之后将学的空间向量的运算体系是完全类比平面向量的运算体系建立的,因此,平面向量的运算是向量的核心内容,起到承上启下的作用.
教学目标
(1)通过物理中力的合成等实例,能抽象形成平面向量向量加法的概念,体会由位移、力的合成到定义向量加法的过程,感悟数学抽象、逻辑推理等素养;
(2)通过平面向量的几何意义探讨加法法则,会画图表示两个向量的和向量,体会法则的重要性及其几何意义,增强对数学思维方法的理解;
(3)通过类比代数运算,从向量加法的定义及几何意义入手,研究向量加法的运算律,并会用其进行向量计算,体会研究向量运算的一般方法.
3. 教学重点及难点
重点:掌握平面向量加法运算及运算法则,理解其几何意义.
难点:向量加法运算律的证明以及应用.
学情分析
学生前面学面向量的定义及表示方法、相等向量平行向量等概念,有一定的知识基础.从向量加法运算研究的路径看,学生有了数的运算的研究经验,对数的运算路径有一定的认识,选择从物理背景引出数学内容,有利于学生更好的理解向量加法的意义,准确把握两个加法法则的特点.
教法学法分析
通过类比实数的运算以及位移的合成、力的合成,以“背景——定义——法则——性质——应用”为研究路径,培养学生发现问题、提出问题、分析问题和解决问题的能力.遵循从特殊到一般的思想方法,有利于学生接受新知识,避免了畏难情绪. 向量运算中的物理背景及蕴含的数形结合思想,帮助学生树立联系的观点,促进对数学整体性的理解.在教学设计中,采取问题引导方式来组织课堂教学.问题的设置给学生留有充分的思考空间,让学生围绕问题主线,通过自主探究达到突出教学重点,突破教学难点.
教学过程
1.创设情境 引入新课
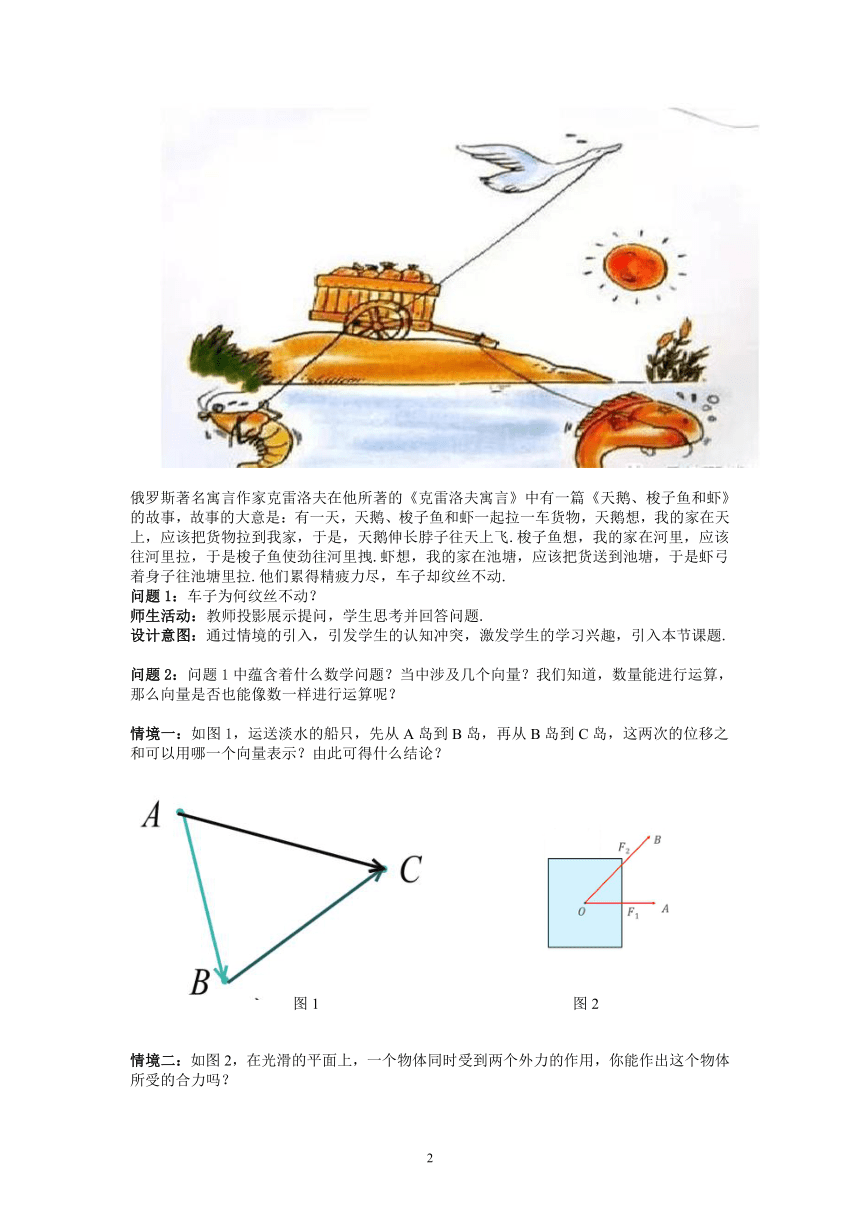
俄罗斯著名寓言作家克雷洛夫在他所著的《克雷洛夫寓言》中有一篇《天鹅、梭子鱼和虾》的故事,故事的大意是:有一天,天鹅、梭子鱼和虾一起拉一车货物,天鹅想,我的家在天上,应该把货物拉到我家,于是,天鹅伸长脖子往天上飞.梭子鱼想,我的家在河里,应该往河里拉,于是梭子鱼使劲往河里拽.虾想,我的家在池塘,应该把货送到池塘,于是虾弓着身子往池塘里拉.他们累得精疲力尽,车子却纹丝不动.
问题1:车子为何纹丝不动?
师生活动:教师投影展示提问,学生思考并回答问题.
设计意图:通过情境的引入,引发学生的认知冲突,激发学生的学习兴趣,引入本节课题.
问题2:问题1中蕴含着什么数学问题?当中涉及几个向量?我们知道,数量能进行运算,那么向量是否也能像数一样进行运算呢?
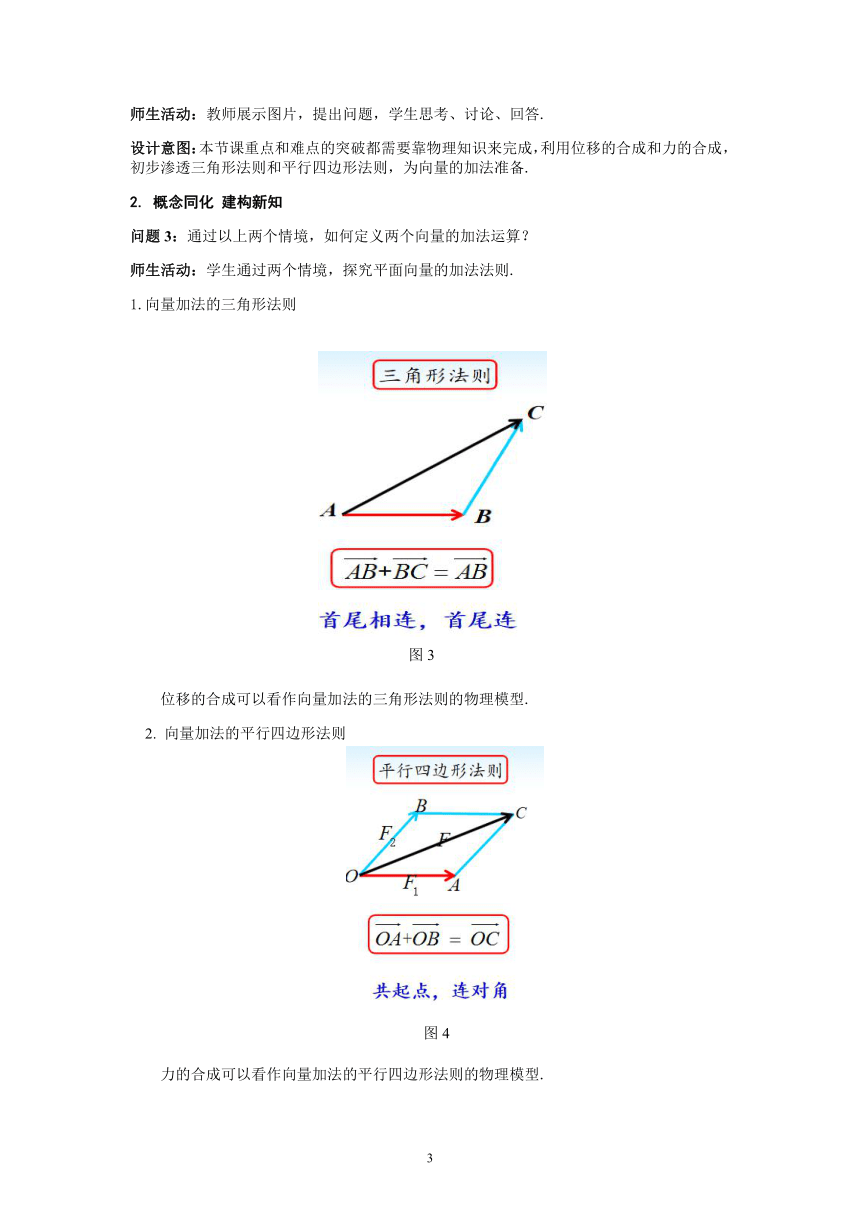
情境一:如图1,运送淡水的船只,先从A岛到B岛,再从B岛到C岛,这两次的位移之和可以用哪一个向量表示?由此可得什么结论?
情境二:如图2,在光滑的平面上,一个物体同时受到两个外力的作用,你能作出这个物体所受的合力吗?
师生活动:教师展示图片,提出问题,学生思考、讨论、回答.
设计意图:本节课重点和难点的突破都需要靠物理知识来完成,利用位移的合成和力的合成,初步渗透三角形法则和平行四边形法则,为向量的加法准备.
2. 概念同化 建构新知
问题3:通过以上两个情境,如何定义两个向量的加法运算?
师生活动:学生通过两个情境,探究平面向量的加法法则.
1.向量加法的三角形法则
位移的合成可以看作向量加法的三角形法则的物理模型.
2. 向量加法的平行四边形法则
力的合成可以看作向量加法的平行四边形法则的物理模型.
设计意图:师生合作,形成向量加法的定义,师生合作探究两个向量的和的作法,突出重点----向量加法的两个法则,利用两个情境探究得出平面向量的加法法则,培养学生迁移能力.
问题4:零向量与任一非零向量,能否求出它们的和向量?
规定:零向量与任一向量,都有.
设计意图:类比数0,规定零向量与任一非零向量的和,使学生理解特殊向量的加法,巩固知识.
问题5:向量加法的平行四边形法则和三角形法则一致吗?为什么?
物理 位移的合成 力的合成
图形
法则 三角形法则 平行四边形法则
口诀 首尾相连,首尾连 共起点,连对角
联系 两法则本质上一致,只是表示形式不同
师生活动:学生思考讨论,教师引导学生回答并展示答案.
设计意图:引导学生思考两个法则的差异,用语言高度概括,突出本节课的重点.
3.辨析理解 深化概念
例1 如图,已知向量 , 不共线时,求作.
师生活动:学生独立完成之后展示交流,进一步熟悉向量加法的两个法则,并引导学生发现两个法则的联系.
变式:如图,已知向量,,求作.
设计意图:培养学生作图能力,同时明确向量加法的三角形法则和平行四边形法则的适用范围,当两个向量共线时,只能用三角形法则,当两个向量不共线时,两个法则皆可.
问题6:观察例题和变式训练的作图结果,你能发现,,之间的关系吗?
设计意图:深化对向量加法运算的认识,明确向量加法与实数加法的本质不同.学生在自主探究、交流合作中解决问题,加深对知识的理解.
问题7:数的加法满足交换律、结合律,向量的加法也满足这些运算律吗?
数 向量
性质
设计意图:明确作图是验证向量加法运算律的有效途径,进一步培养学生观察、类比等能力,同时让学生感受“数学发现”的乐趣.
4.新知运用 巩固内化
例2 、、、、、为平面上的任意点,化简下列各式:
(1)
(2)
(3)
设计意图:提高学生的运算能力,并将三角形法则进行推广至多边形.
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输。如图,一艘船从长江A地
出发,垂直于对岸航行,航行速度的大小为15km/h,同时江水的速度为向东6km/h.
(1)用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行速度的大小与方向(用与江水速度间的夹角表示)
学生:思考并回答思路。
教师:规范解答
解:(1)如图,表示船速, 表示江水速度,以AD,AB为邻边作平行四边形ABCD,则表示船实际航行的速度.
(2)在直角三角形ABC中,.
因为,
答:船实际航行速度大小为,方向与江水速度间的夹角约为
教师:你能总结一下解决实际问题的步骤吗?
设计意图:以学生熟悉的生活问题作为例题,学会用数学的眼光观察世界,从中抽象出数学模型后再求解,最后将数学问题的解还原为实际问题的解,体会向量在解决实际问题的作用,培养数学建模、数学运算等核心素养.
5. 归纳总结 反思提升
教师:本节课你有哪些收获?请大家从知识和数学思想方法等方面小结.
研究知识
研究方法:类比实数的运算提出问题串.
数学思想:类比、数形结合、分类讨论.
设计意图:引导学生共同回顾总结,培养学生良好的学习习惯,同时也培养学生口头表达能力和概括能力.
作业设计 :
(1)教材第22—23页习题6.2第1,2,3,6,10题;
(2)阅读课本,进一步理解向量加法研究思路,体会向量运算与数运算的异同.
教学内容分析
地位与作用
本节课选自人教A版必修第二册第六章“平面向量”第二节“平面向量的线性运算”第一课时.向量既有代数意义又有几何意义,作为沟通代数几何三角的桥梁,蕴含了数形结合、类比、归纳等数学思想方法,是培养学生数学抽象、逻辑推理、数学运算、直观想象等数学学科核心素养的极好载体.本单元将会从代数几何两方面对运算对象进行扩展,首先学习平面向量的加法运算,接着就是减法运算和数乘运算,平面向量的数量积,平面向量投影和投影向量,会利用向量运算判断两个向量的平行与垂直、求两个向量的夹角.之后将学的空间向量的运算体系是完全类比平面向量的运算体系建立的,因此,平面向量的运算是向量的核心内容,起到承上启下的作用.
教学目标
(1)通过物理中力的合成等实例,能抽象形成平面向量向量加法的概念,体会由位移、力的合成到定义向量加法的过程,感悟数学抽象、逻辑推理等素养;
(2)通过平面向量的几何意义探讨加法法则,会画图表示两个向量的和向量,体会法则的重要性及其几何意义,增强对数学思维方法的理解;
(3)通过类比代数运算,从向量加法的定义及几何意义入手,研究向量加法的运算律,并会用其进行向量计算,体会研究向量运算的一般方法.
3. 教学重点及难点
重点:掌握平面向量加法运算及运算法则,理解其几何意义.
难点:向量加法运算律的证明以及应用.
学情分析
学生前面学面向量的定义及表示方法、相等向量平行向量等概念,有一定的知识基础.从向量加法运算研究的路径看,学生有了数的运算的研究经验,对数的运算路径有一定的认识,选择从物理背景引出数学内容,有利于学生更好的理解向量加法的意义,准确把握两个加法法则的特点.
教法学法分析
通过类比实数的运算以及位移的合成、力的合成,以“背景——定义——法则——性质——应用”为研究路径,培养学生发现问题、提出问题、分析问题和解决问题的能力.遵循从特殊到一般的思想方法,有利于学生接受新知识,避免了畏难情绪. 向量运算中的物理背景及蕴含的数形结合思想,帮助学生树立联系的观点,促进对数学整体性的理解.在教学设计中,采取问题引导方式来组织课堂教学.问题的设置给学生留有充分的思考空间,让学生围绕问题主线,通过自主探究达到突出教学重点,突破教学难点.
教学过程
1.创设情境 引入新课
俄罗斯著名寓言作家克雷洛夫在他所著的《克雷洛夫寓言》中有一篇《天鹅、梭子鱼和虾》的故事,故事的大意是:有一天,天鹅、梭子鱼和虾一起拉一车货物,天鹅想,我的家在天上,应该把货物拉到我家,于是,天鹅伸长脖子往天上飞.梭子鱼想,我的家在河里,应该往河里拉,于是梭子鱼使劲往河里拽.虾想,我的家在池塘,应该把货送到池塘,于是虾弓着身子往池塘里拉.他们累得精疲力尽,车子却纹丝不动.
问题1:车子为何纹丝不动?
师生活动:教师投影展示提问,学生思考并回答问题.
设计意图:通过情境的引入,引发学生的认知冲突,激发学生的学习兴趣,引入本节课题.
问题2:问题1中蕴含着什么数学问题?当中涉及几个向量?我们知道,数量能进行运算,那么向量是否也能像数一样进行运算呢?
情境一:如图1,运送淡水的船只,先从A岛到B岛,再从B岛到C岛,这两次的位移之和可以用哪一个向量表示?由此可得什么结论?
情境二:如图2,在光滑的平面上,一个物体同时受到两个外力的作用,你能作出这个物体所受的合力吗?
师生活动:教师展示图片,提出问题,学生思考、讨论、回答.
设计意图:本节课重点和难点的突破都需要靠物理知识来完成,利用位移的合成和力的合成,初步渗透三角形法则和平行四边形法则,为向量的加法准备.
2. 概念同化 建构新知
问题3:通过以上两个情境,如何定义两个向量的加法运算?
师生活动:学生通过两个情境,探究平面向量的加法法则.
1.向量加法的三角形法则
位移的合成可以看作向量加法的三角形法则的物理模型.
2. 向量加法的平行四边形法则
力的合成可以看作向量加法的平行四边形法则的物理模型.
设计意图:师生合作,形成向量加法的定义,师生合作探究两个向量的和的作法,突出重点----向量加法的两个法则,利用两个情境探究得出平面向量的加法法则,培养学生迁移能力.
问题4:零向量与任一非零向量,能否求出它们的和向量?
规定:零向量与任一向量,都有.
设计意图:类比数0,规定零向量与任一非零向量的和,使学生理解特殊向量的加法,巩固知识.
问题5:向量加法的平行四边形法则和三角形法则一致吗?为什么?
物理 位移的合成 力的合成
图形
法则 三角形法则 平行四边形法则
口诀 首尾相连,首尾连 共起点,连对角
联系 两法则本质上一致,只是表示形式不同
师生活动:学生思考讨论,教师引导学生回答并展示答案.
设计意图:引导学生思考两个法则的差异,用语言高度概括,突出本节课的重点.
3.辨析理解 深化概念
例1 如图,已知向量 , 不共线时,求作.
师生活动:学生独立完成之后展示交流,进一步熟悉向量加法的两个法则,并引导学生发现两个法则的联系.
变式:如图,已知向量,,求作.
设计意图:培养学生作图能力,同时明确向量加法的三角形法则和平行四边形法则的适用范围,当两个向量共线时,只能用三角形法则,当两个向量不共线时,两个法则皆可.
问题6:观察例题和变式训练的作图结果,你能发现,,之间的关系吗?
设计意图:深化对向量加法运算的认识,明确向量加法与实数加法的本质不同.学生在自主探究、交流合作中解决问题,加深对知识的理解.
问题7:数的加法满足交换律、结合律,向量的加法也满足这些运算律吗?
数 向量
性质
设计意图:明确作图是验证向量加法运算律的有效途径,进一步培养学生观察、类比等能力,同时让学生感受“数学发现”的乐趣.
4.新知运用 巩固内化
例2 、、、、、为平面上的任意点,化简下列各式:
(1)
(2)
(3)
设计意图:提高学生的运算能力,并将三角形法则进行推广至多边形.
例3 长江两岸之间没有大桥的地方,常常通过轮渡进行运输。如图,一艘船从长江A地
出发,垂直于对岸航行,航行速度的大小为15km/h,同时江水的速度为向东6km/h.
(1)用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行速度的大小与方向(用与江水速度间的夹角表示)
学生:思考并回答思路。
教师:规范解答
解:(1)如图,表示船速, 表示江水速度,以AD,AB为邻边作平行四边形ABCD,则表示船实际航行的速度.
(2)在直角三角形ABC中,.
因为,
答:船实际航行速度大小为,方向与江水速度间的夹角约为
教师:你能总结一下解决实际问题的步骤吗?
设计意图:以学生熟悉的生活问题作为例题,学会用数学的眼光观察世界,从中抽象出数学模型后再求解,最后将数学问题的解还原为实际问题的解,体会向量在解决实际问题的作用,培养数学建模、数学运算等核心素养.
5. 归纳总结 反思提升
教师:本节课你有哪些收获?请大家从知识和数学思想方法等方面小结.
研究知识
研究方法:类比实数的运算提出问题串.
数学思想:类比、数形结合、分类讨论.
设计意图:引导学生共同回顾总结,培养学生良好的学习习惯,同时也培养学生口头表达能力和概括能力.
作业设计 :
(1)教材第22—23页习题6.2第1,2,3,6,10题;
(2)阅读课本,进一步理解向量加法研究思路,体会向量运算与数运算的异同.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
