第五章《相交线与平行线》单元复习与能力提升解答题靶向练习 (无答案)人教版数学七年级下册
文档属性
| 名称 | 第五章《相交线与平行线》单元复习与能力提升解答题靶向练习 (无答案)人教版数学七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 291.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 21:12:01 | ||
图片预览


文档简介
人教版七年级下册数学《相交线与平行线》单元复习
与能力提升解答题靶向练习
题型一:尺规作图
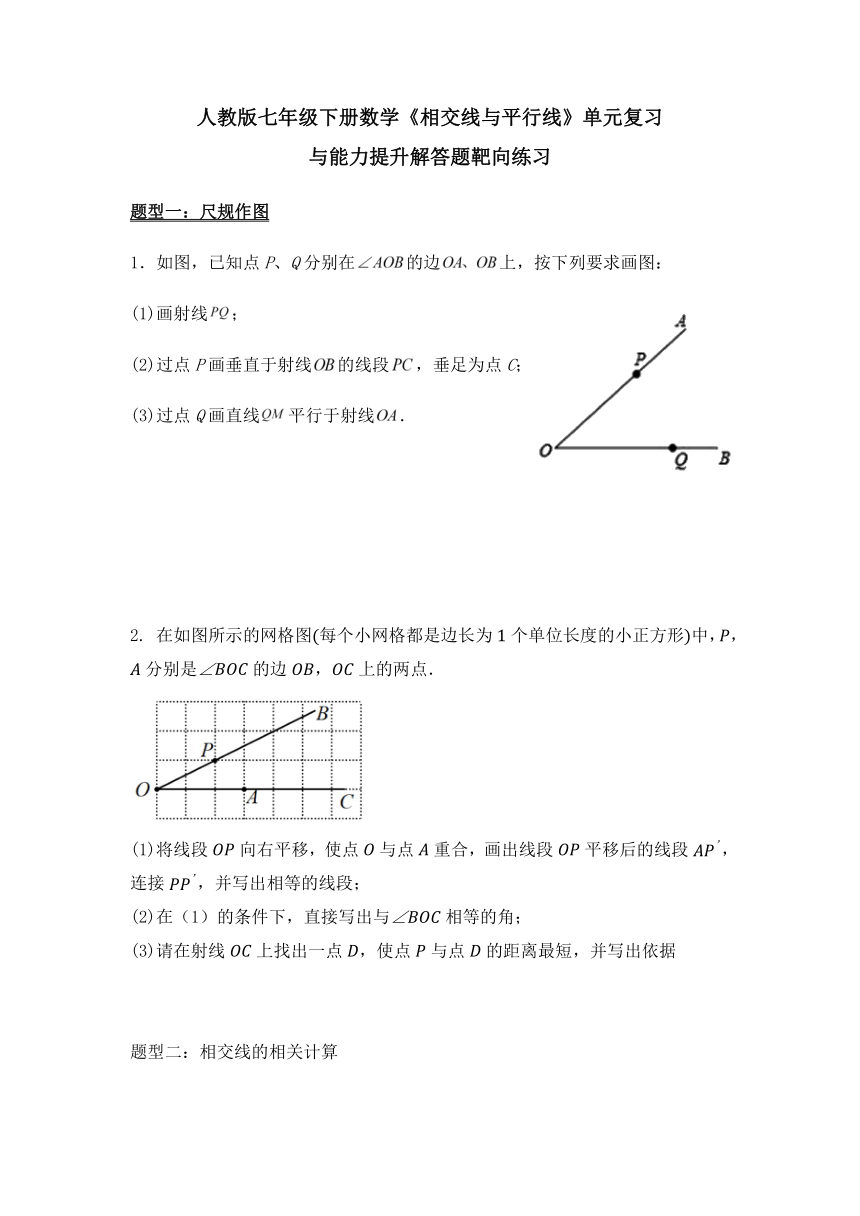
1.如图,已知点P、Q分别在的边上,按下列要求画图:
(1)画射线;
(2)过点P画垂直于射线的线段,垂足为点C;
(3)过点Q画直线平行于射线.
2. 在如图所示的网格图每个小网格都是边长为个单位长度的小正方形中,,分别是的边,上的两点.
(1)将线段向右平移,使点与点重合,画出线段平移后的线段,连接,并写出相等的线段;
(2)在(1)的条件下,直接写出与相等的角;
(3)请在射线上找出一点,使点与点的距离最短,并写出依据
题型二:相交线的相关计算
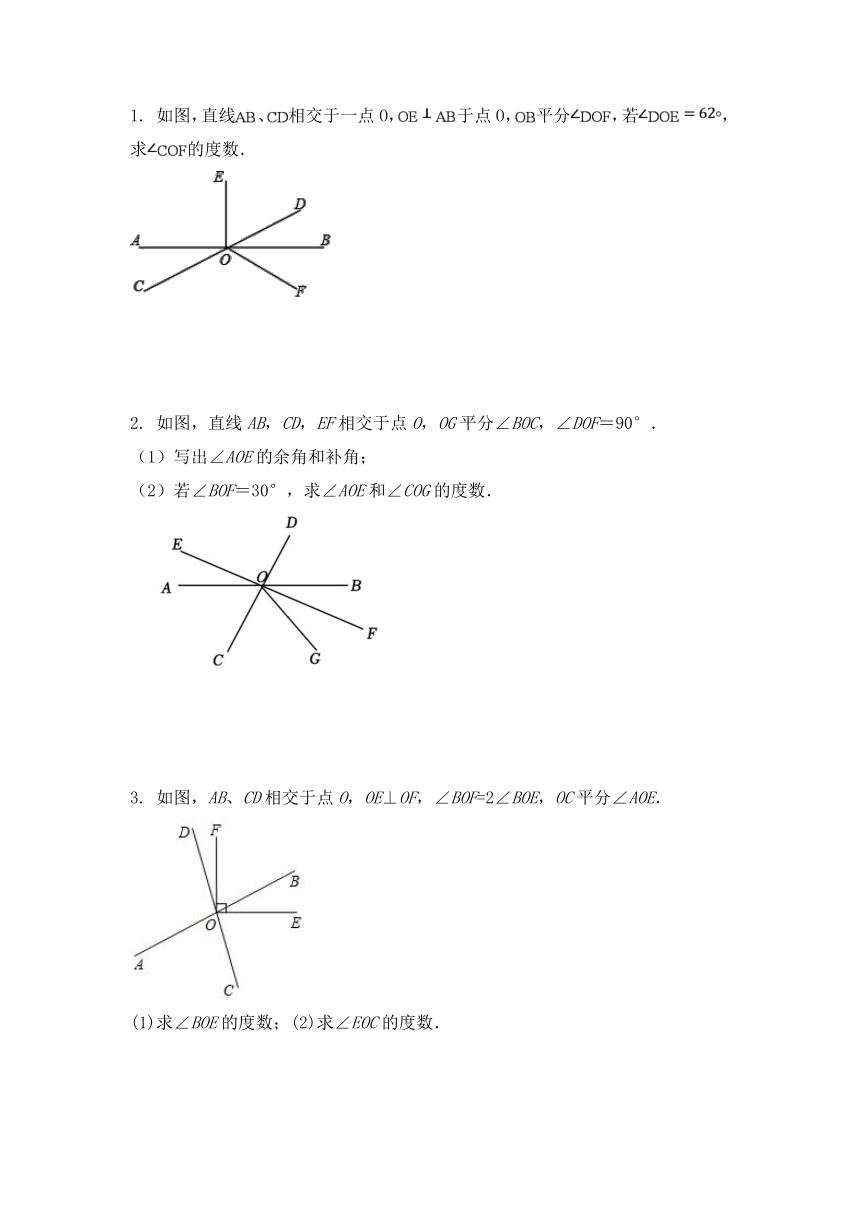
1. 如图,直线、相交于一点O,于点O,平分,若,求的度数.
2. 如图,直线AB,CD,EF相交于点O,OG平分∠BOC,∠DOF=90°.
(1)写出∠AOE的余角和补角;
(2)若∠BOF=30°,求∠AOE和∠COG的度数.
3. 如图,AB、CD相交于点O,OE⊥OF,∠BOF=2∠BOE,OC平分∠AOE.
(1)求∠BOE的度数;(2)求∠EOC的度数.
4. 已知直线经过点,,是的平分线.
(1)如图1,若,求;
(2)如图1,若,直接写出______;(用含的式子表示)
(3)将图1中的绕顶点顺时针旋转到图2的位置,其他条件不变,(2)中的结论是否还成立?试说明理由.
题型三:平行线的计算
1. 如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,已知∠1+∠2=90°,且∠2:∠3=2:5.
(1)求∠BOF的度数;
(2)试说明AB∥CD的理由.
2.已知:如图,∠CDG=∠B,AD⊥BC于点D,EF⊥BC于点F.
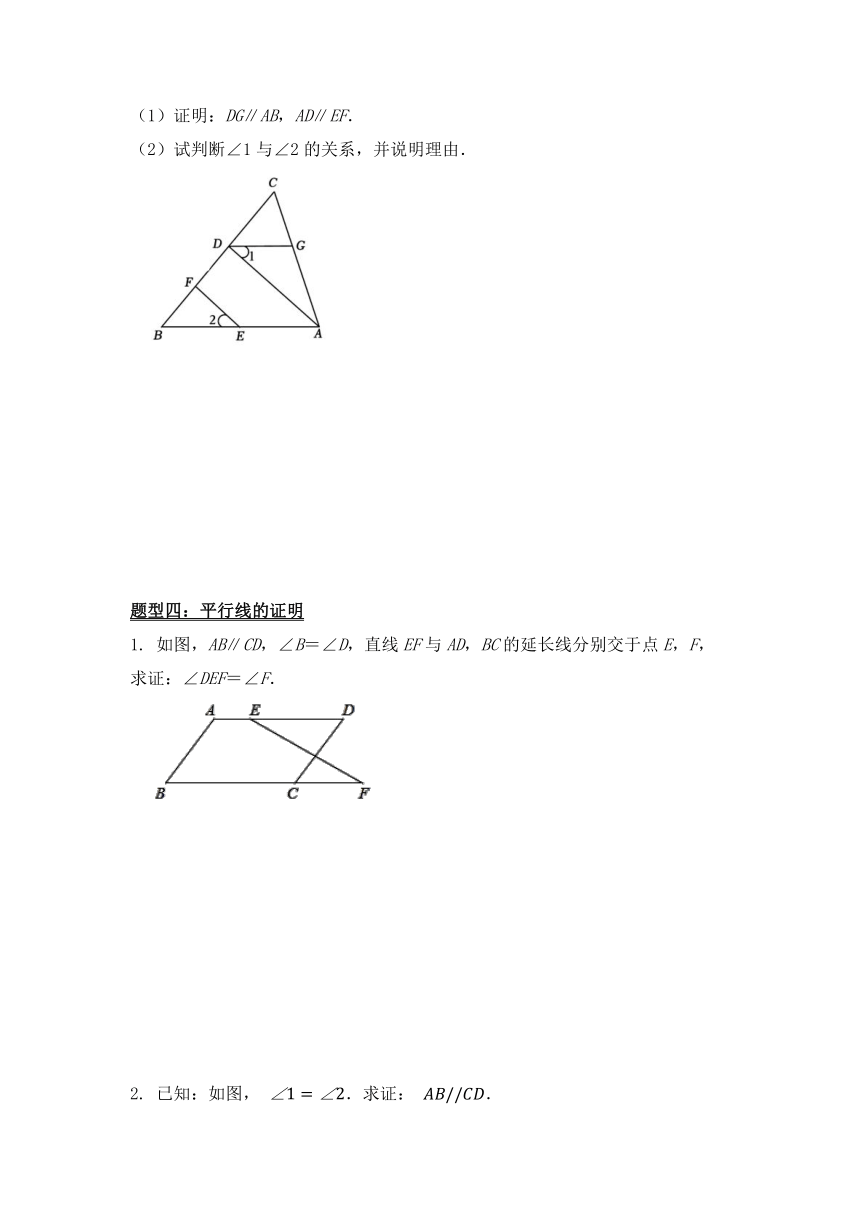
(1)证明:DG∥AB,AD∥EF.
(2)试判断∠1与∠2的关系,并说明理由.
题型四:平行线的证明
如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F,
求证:∠DEF=∠F.
2. 已知:如图, .求证: .
分析:如图,欲证,只要证______.
证明: ,(已知)
又,( )
__________.( )
.(__________,____________)
3. 如图,点B,C在线段的异侧,点E,F分别是线段,上的点,已知,.
(1)求证:;
(2)若,求证:;
(3)在(2)的条件下,若,求的度数.
题型五:相交线与平行线的综合问题
1. 如图,处是一钻井平台,位于东营港口的北偏东方向上,与港口相距海里,一艘摩托艇从出发,自西向东航行至时,改变航向以每小时海里的速度沿方向行进,此时位于的北偏西方向,则从到达需要多少小时?
2. 如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.
(1)求证:AD∥BC;
(2)若∠1=36°,求∠2的度数.
3. 已知:如图所示,∠1和∠D互余,∠C和∠D互余.
求证:AB∥CD.
证明:∵∠1和∠D互余(已知),
∴∠1+∠D=90°( ).
∵∠C和∠D互余(已知),
∴∠C+∠D=90°( ).
∴∠1=∠C( ),
∴AB∥CD( ).
4.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为______;
(2)当△PMN所放位置如图②所示时,求证:∠PFD ∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
5. 如图1,四边形为一张长方形纸片.
(1)如图2,将长方形纸片剪两刀,剪出三个角(),则__________°.
(2)如图3,将长方形纸片剪三刀,剪出四个角(),则__________°.
(3)如图4,将长方形纸片剪四刀,剪出五个角(),则___________°.
(4)根据前面探索出的规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是____________°.
与能力提升解答题靶向练习
题型一:尺规作图
1.如图,已知点P、Q分别在的边上,按下列要求画图:
(1)画射线;
(2)过点P画垂直于射线的线段,垂足为点C;
(3)过点Q画直线平行于射线.
2. 在如图所示的网格图每个小网格都是边长为个单位长度的小正方形中,,分别是的边,上的两点.
(1)将线段向右平移,使点与点重合,画出线段平移后的线段,连接,并写出相等的线段;
(2)在(1)的条件下,直接写出与相等的角;
(3)请在射线上找出一点,使点与点的距离最短,并写出依据
题型二:相交线的相关计算
1. 如图,直线、相交于一点O,于点O,平分,若,求的度数.
2. 如图,直线AB,CD,EF相交于点O,OG平分∠BOC,∠DOF=90°.
(1)写出∠AOE的余角和补角;
(2)若∠BOF=30°,求∠AOE和∠COG的度数.
3. 如图,AB、CD相交于点O,OE⊥OF,∠BOF=2∠BOE,OC平分∠AOE.
(1)求∠BOE的度数;(2)求∠EOC的度数.
4. 已知直线经过点,,是的平分线.
(1)如图1,若,求;
(2)如图1,若,直接写出______;(用含的式子表示)
(3)将图1中的绕顶点顺时针旋转到图2的位置,其他条件不变,(2)中的结论是否还成立?试说明理由.
题型三:平行线的计算
1. 如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,已知∠1+∠2=90°,且∠2:∠3=2:5.
(1)求∠BOF的度数;
(2)试说明AB∥CD的理由.
2.已知:如图,∠CDG=∠B,AD⊥BC于点D,EF⊥BC于点F.
(1)证明:DG∥AB,AD∥EF.
(2)试判断∠1与∠2的关系,并说明理由.
题型四:平行线的证明
如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F,
求证:∠DEF=∠F.
2. 已知:如图, .求证: .
分析:如图,欲证,只要证______.
证明: ,(已知)
又,( )
__________.( )
.(__________,____________)
3. 如图,点B,C在线段的异侧,点E,F分别是线段,上的点,已知,.
(1)求证:;
(2)若,求证:;
(3)在(2)的条件下,若,求的度数.
题型五:相交线与平行线的综合问题
1. 如图,处是一钻井平台,位于东营港口的北偏东方向上,与港口相距海里,一艘摩托艇从出发,自西向东航行至时,改变航向以每小时海里的速度沿方向行进,此时位于的北偏西方向,则从到达需要多少小时?
2. 如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.
(1)求证:AD∥BC;
(2)若∠1=36°,求∠2的度数.
3. 已知:如图所示,∠1和∠D互余,∠C和∠D互余.
求证:AB∥CD.
证明:∵∠1和∠D互余(已知),
∴∠1+∠D=90°( ).
∵∠C和∠D互余(已知),
∴∠C+∠D=90°( ).
∴∠1=∠C( ),
∴AB∥CD( ).
4.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为______;
(2)当△PMN所放位置如图②所示时,求证:∠PFD ∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
5. 如图1,四边形为一张长方形纸片.
(1)如图2,将长方形纸片剪两刀,剪出三个角(),则__________°.
(2)如图3,将长方形纸片剪三刀,剪出四个角(),则__________°.
(3)如图4,将长方形纸片剪四刀,剪出五个角(),则___________°.
(4)根据前面探索出的规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是____________°.
