2023—2024学年人教版数学八年级上册知识分类训练 12.3 角平分线的性质(含详案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册知识分类训练 12.3 角平分线的性质(含详案) |  | |
| 格式 | doc | ||
| 文件大小 | 446.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 07:01:04 | ||
图片预览



文档简介
人教版2024年八年级上册知识分类训练
12.3 角平分线的性质
1、角平分线的定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
2、角平分线的性质:角的平分线上的点到这个角的两边的距离相等。
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
4、角平分线的判定方法:角的内部到角的两边的距离相等的点在角的平分线上。
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
5、尺规作角的平分线:
画法:①以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
②分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.
③作射线OC.
所以,射线OC即为所求.
针对训练
1.如图,OC平分∠AOB,点P在OC上,PD⊥OB,PD=2,则点P到OA的距离是( )
A.4 B.3 C.2 D.1
2.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )
A.12 B.18 C.24 D.36
3.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=4,则PQ的长不可能是( )
A.3.9 B.4 C.4.3 D.5.5
4.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为( )
A.1 B.2 C.3 D.4
5.如图,在四边形ABCD中,∠A=90°,AD=4,BC=6,对角线BD平分∠ABC,则△BCD的面积为( )
A.15 B.12 C.8 D.6
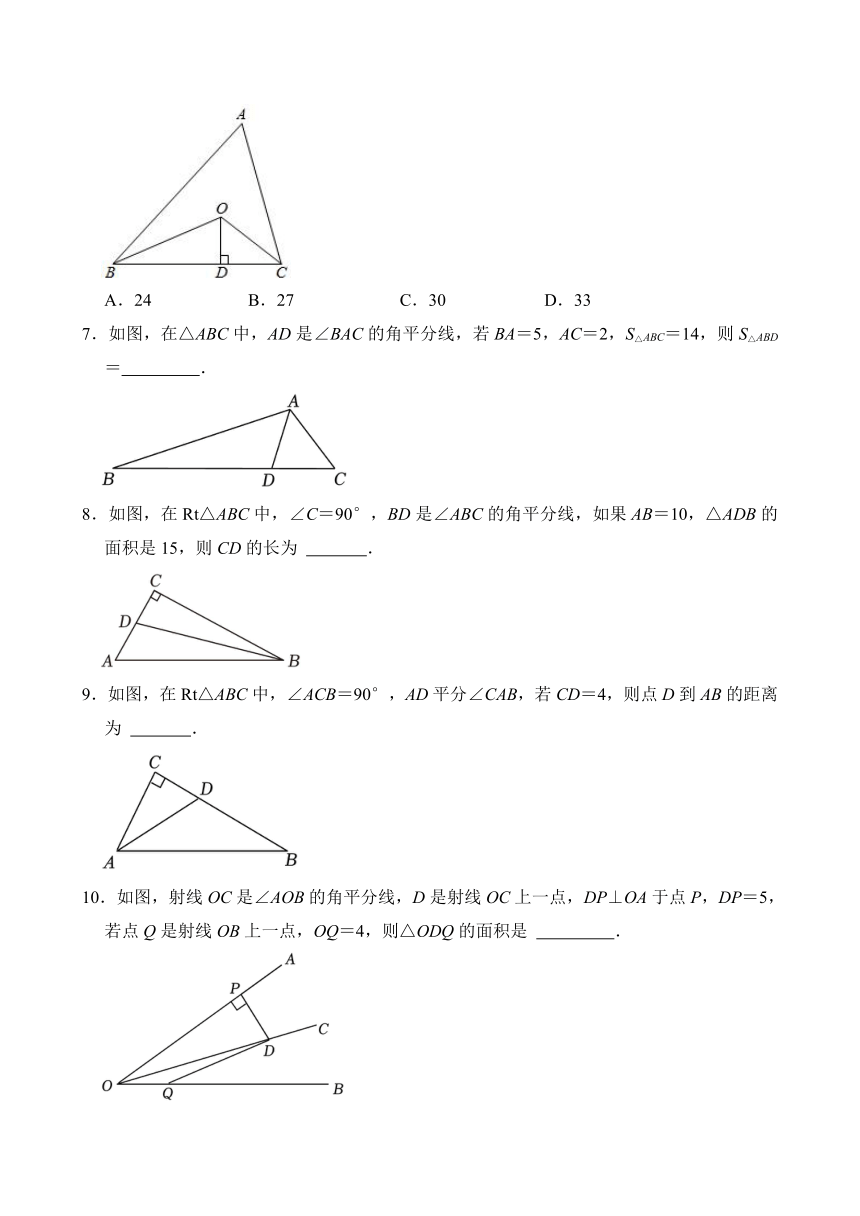
6.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
7.如图,在△ABC中,AD是∠BAC的角平分线,若BA=5,AC=2,S△ABC=14,则S△ABD= .
8.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的角平分线,如果AB=10,△ADB的面积是15,则CD的长为 .
9.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离为 .
10.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .
11.如图,在△ABC中,BD是△ABC的角平分线,DE⊥AB于点E,DE=2.AB=6.BC=4,求△ABC的面积.
12.如图在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB于点,DF⊥AC于点F.
求证:AD是△ABC的角平分线.
13.如图,CB=CD,∠D+∠ABC=180°,CE⊥AD于E,CF⊥AB交AB的延长线于点F.求证:AC平分∠DAB.
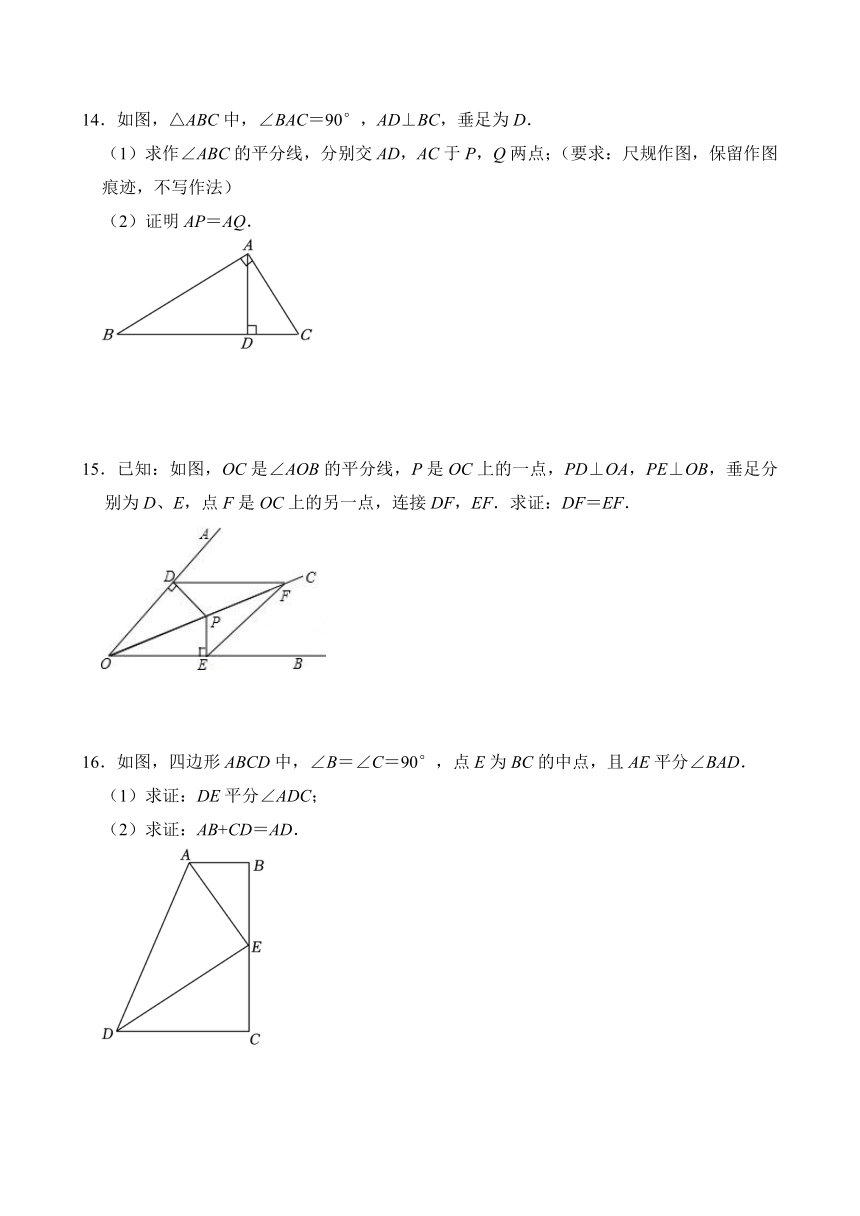
14.如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.
15.已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
16.如图,四边形ABCD中,∠B=∠C=90°,点E为BC的中点,且AE平分∠BAD.
(1)求证:DE平分∠ADC;
(2)求证:AB+CD=AD.
17.如图,△ABC中,点D在边BC延长线上,∠ACB=110°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=55°.
(1)求∠ACE的度数;
(2)求证:AE平分∠CAF;
(3)若AC+CD=14,AB=8.5,且S△ACD=21,求△ABE的面积.
参考答案
1.解:过P作PE⊥AO于E,
∵OC平分∠AOB,点P在OC上,PD⊥OB,
∴PE=PD=2,
∴点P到OA的距离是2.
故选:C.
2.解:过点G作GH⊥AB于点H,
根据题意得,AF是∠CAB的角平分线,
∵∠C=90°,
∴AC⊥CG,
∵GH⊥AB,
∴CG=GH,
∵CG=3,
∴,
故选:B.
3.解:∵OP平分∠MON,PA⊥ON于点A,PA=4,
∴当PQ⊥AM时,PQ=PA=4,
∴PQ≥4,
∴PQ的长不可能3.9.
故选:A.
4.解:
过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,
∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,
∴PQ=PW,PW=PR,
∴PR=PQ,
∵点P到AC的距离为3,
∴PQ=PR=3,
则点P到AB的距离为3,
故选:C.
5.解:过点D作DE⊥BC,垂足为E,
∵BD平分∠ABC,DE⊥BC,DA⊥AB,
∴DE=DA=4,
∵BC=6,
∴△BCD的面积=BC DE=×6×4=12,
故选:B.
6.解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×OE×AB+×OD×BC+×OF×AC
=(AB+BC+AC),
∵△ABC的周长是18,
∴S△ABC=×18=27(cm2).
故选:B.
7.解:过点D作DE⊥AB,DF⊥AC于点E,F,
∵AD是∠BAC的角平分线,
∴DE=DF,
设DE=DF=h,
∵BA=5,AC=2,S△ABC=14,
∴AB h+AC h=14,即×5h+×2h=14,
解得h=4,
∴S△ABD=AB DE=×5×4=10.
故答案为:10.
8.解:如图,过点D作DE⊥AB于点E,
∵AB=10,△ADB的面积是15,
∴,
∴DE=3,
在Rt△ABC中,∠C=90°,BD是∠ABC的角平分线,
∴CD=DE=3,
故答案为:3.
9.解:过点D,作DE⊥AB,交AB于点E,
∵∠ACB=90°,AD平分∠CAB,
∴DE=CD=4,
故答案为:4.
10.解:作DH⊥OB于点H,
∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,
∴DH=DP=5,
∴△ODQ的面积=OQ DH=4×5=10,
故答案为:10.
11.解:如图,过点D作DF⊥BC于点F.
∵BD是△ABC 的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=2,
又∵AB=6,BC=4,
∴
=.
12.证明:∵点D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF,
即点D到AB和AC的距离相等,
∴AD是△ABC的角平分线.
13.证明:∵CE⊥AD于E,CF⊥AB,
∴∠DEC=∠CFB=90°,
∵∠D+∠ABC=180°,∠CBF+∠ABC=180°,
∴∠D=∠CBF,
在△CDE与△CBF中,
,
∴△CDE≌△CBF(AAS),
∴CE=CF,
∴AC平分∠DAB.
14.(1)解:如图所示,BQ为所求作;
(2)证明:∵BQ平分∠ABC,
∴∠ABQ=∠CBQ,
∵∠BAC=90°
∴∠AQP+∠ABQ=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠CBQ+∠BPD=90°,
∵∠ABQ=∠CBQ,
∴∠AQP=∠BPD,
又∵∠BPD=∠APQ,
∴∠AQP=∠APQ,
∴AP=AQ.
15.证明:∵OP是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,,
∴△ODF≌△OEF(SAS),
∴DF=EF.
16.证明:(1)如图,过点E作EF⊥AD于F,
∵∠B=90°,AE平分∠DAB,
∴BE=EF,
∵E是BC的中点,
∴BE=CE,
∴CE=EF,
又∵∠C=90°,EF⊥AD,
∴DE是∠ADC的平分线.
(2)∵AE平分∠BAD,DE平分∠ADC,EF⊥AD,∠B=∠C=90°,
∴AB=AF,DC=DF,
∴AB+CD=AF+FD=AD.
17.(1)解:∵∠ACB=110°,
∴∠ACD=180°﹣110°=70°,
∵EH⊥BD,
∴∠CHE=90°,
∵∠CEH=55°,
∴∠ECH=90°﹣55°=35°,
∴∠ACE=180°﹣35°﹣110°=35°;
(2)证明:过E点分别作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=∠ECH=40°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF;
(3)解:∵AC+CD=14,S△ACD=21,EM=EN=EH,
∴S△ACD=S△ACE+S△CED=AC EN+CD EH=(AC+CD) EM=21,
即,
解得EM=3,
∵AB=8.5,
∴S△ABE=AB EM=.
12.3 角平分线的性质
1、角平分线的定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
2、角平分线的性质:角的平分线上的点到这个角的两边的距离相等。
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
4、角平分线的判定方法:角的内部到角的两边的距离相等的点在角的平分线上。
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
5、尺规作角的平分线:
画法:①以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
②分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.
③作射线OC.
所以,射线OC即为所求.
针对训练
1.如图,OC平分∠AOB,点P在OC上,PD⊥OB,PD=2,则点P到OA的距离是( )
A.4 B.3 C.2 D.1
2.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )
A.12 B.18 C.24 D.36
3.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=4,则PQ的长不可能是( )
A.3.9 B.4 C.4.3 D.5.5
4.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为( )
A.1 B.2 C.3 D.4
5.如图,在四边形ABCD中,∠A=90°,AD=4,BC=6,对角线BD平分∠ABC,则△BCD的面积为( )
A.15 B.12 C.8 D.6
6.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
7.如图,在△ABC中,AD是∠BAC的角平分线,若BA=5,AC=2,S△ABC=14,则S△ABD= .
8.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的角平分线,如果AB=10,△ADB的面积是15,则CD的长为 .
9.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离为 .
10.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .
11.如图,在△ABC中,BD是△ABC的角平分线,DE⊥AB于点E,DE=2.AB=6.BC=4,求△ABC的面积.
12.如图在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB于点,DF⊥AC于点F.
求证:AD是△ABC的角平分线.
13.如图,CB=CD,∠D+∠ABC=180°,CE⊥AD于E,CF⊥AB交AB的延长线于点F.求证:AC平分∠DAB.
14.如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.
15.已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
16.如图,四边形ABCD中,∠B=∠C=90°,点E为BC的中点,且AE平分∠BAD.
(1)求证:DE平分∠ADC;
(2)求证:AB+CD=AD.
17.如图,△ABC中,点D在边BC延长线上,∠ACB=110°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=55°.
(1)求∠ACE的度数;
(2)求证:AE平分∠CAF;
(3)若AC+CD=14,AB=8.5,且S△ACD=21,求△ABE的面积.
参考答案
1.解:过P作PE⊥AO于E,
∵OC平分∠AOB,点P在OC上,PD⊥OB,
∴PE=PD=2,
∴点P到OA的距离是2.
故选:C.
2.解:过点G作GH⊥AB于点H,
根据题意得,AF是∠CAB的角平分线,
∵∠C=90°,
∴AC⊥CG,
∵GH⊥AB,
∴CG=GH,
∵CG=3,
∴,
故选:B.
3.解:∵OP平分∠MON,PA⊥ON于点A,PA=4,
∴当PQ⊥AM时,PQ=PA=4,
∴PQ≥4,
∴PQ的长不可能3.9.
故选:A.
4.解:
过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,
∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,
∴PQ=PW,PW=PR,
∴PR=PQ,
∵点P到AC的距离为3,
∴PQ=PR=3,
则点P到AB的距离为3,
故选:C.
5.解:过点D作DE⊥BC,垂足为E,
∵BD平分∠ABC,DE⊥BC,DA⊥AB,
∴DE=DA=4,
∵BC=6,
∴△BCD的面积=BC DE=×6×4=12,
故选:B.
6.解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×OE×AB+×OD×BC+×OF×AC
=(AB+BC+AC),
∵△ABC的周长是18,
∴S△ABC=×18=27(cm2).
故选:B.
7.解:过点D作DE⊥AB,DF⊥AC于点E,F,
∵AD是∠BAC的角平分线,
∴DE=DF,
设DE=DF=h,
∵BA=5,AC=2,S△ABC=14,
∴AB h+AC h=14,即×5h+×2h=14,
解得h=4,
∴S△ABD=AB DE=×5×4=10.
故答案为:10.
8.解:如图,过点D作DE⊥AB于点E,
∵AB=10,△ADB的面积是15,
∴,
∴DE=3,
在Rt△ABC中,∠C=90°,BD是∠ABC的角平分线,
∴CD=DE=3,
故答案为:3.
9.解:过点D,作DE⊥AB,交AB于点E,
∵∠ACB=90°,AD平分∠CAB,
∴DE=CD=4,
故答案为:4.
10.解:作DH⊥OB于点H,
∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,
∴DH=DP=5,
∴△ODQ的面积=OQ DH=4×5=10,
故答案为:10.
11.解:如图,过点D作DF⊥BC于点F.
∵BD是△ABC 的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=2,
又∵AB=6,BC=4,
∴
=.
12.证明:∵点D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF,
即点D到AB和AC的距离相等,
∴AD是△ABC的角平分线.
13.证明:∵CE⊥AD于E,CF⊥AB,
∴∠DEC=∠CFB=90°,
∵∠D+∠ABC=180°,∠CBF+∠ABC=180°,
∴∠D=∠CBF,
在△CDE与△CBF中,
,
∴△CDE≌△CBF(AAS),
∴CE=CF,
∴AC平分∠DAB.
14.(1)解:如图所示,BQ为所求作;
(2)证明:∵BQ平分∠ABC,
∴∠ABQ=∠CBQ,
∵∠BAC=90°
∴∠AQP+∠ABQ=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠CBQ+∠BPD=90°,
∵∠ABQ=∠CBQ,
∴∠AQP=∠BPD,
又∵∠BPD=∠APQ,
∴∠AQP=∠APQ,
∴AP=AQ.
15.证明:∵OP是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,,
∴△ODF≌△OEF(SAS),
∴DF=EF.
16.证明:(1)如图,过点E作EF⊥AD于F,
∵∠B=90°,AE平分∠DAB,
∴BE=EF,
∵E是BC的中点,
∴BE=CE,
∴CE=EF,
又∵∠C=90°,EF⊥AD,
∴DE是∠ADC的平分线.
(2)∵AE平分∠BAD,DE平分∠ADC,EF⊥AD,∠B=∠C=90°,
∴AB=AF,DC=DF,
∴AB+CD=AF+FD=AD.
17.(1)解:∵∠ACB=110°,
∴∠ACD=180°﹣110°=70°,
∵EH⊥BD,
∴∠CHE=90°,
∵∠CEH=55°,
∴∠ECH=90°﹣55°=35°,
∴∠ACE=180°﹣35°﹣110°=35°;
(2)证明:过E点分别作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=∠ECH=40°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF;
(3)解:∵AC+CD=14,S△ACD=21,EM=EN=EH,
∴S△ACD=S△ACE+S△CED=AC EN+CD EH=(AC+CD) EM=21,
即,
解得EM=3,
∵AB=8.5,
∴S△ABE=AB EM=.
