人教版数学八年级上册 第12 章全等三角形 测试卷(含答案)
文档属性
| 名称 | 人教版数学八年级上册 第12 章全等三角形 测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 884.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 00:00:00 | ||
图片预览


文档简介
第12 章测试卷
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.如图,在下列4个正方形图案中,与左边正方形图案全等的图案是( )
2.如图,已知△ACE≌△DBF,下列结论中正确的个数是( )
①AC=DB;②AB=DC;③∠1=∠2;④AE∥DF;⑤S△NCE=S△DFB;⑥BC=AE;⑦BF∥EC.
A.4 B.5 C.6 D.7
3.如图,点 D,E分别在线段AB,AC上,CD与BE 相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B. AD=AE C. BD=CE D. BE=CD
4.如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
A. SSS B. SAS C. HL D. AAS
5.已知OP 是∠AOB 的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )
A. PN<3 B. PN>3 C. PN≥3 D. PN≤3
6.如图,在四边形ABCD 中,E是BC 的中点,连接AC,AE,若AB=AC,AE=CD,AD=CE,则图中的全等三角形有( )
A.0对 B.1对 C.2对 D.3对
7.如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于( )
A.585° B.540° C.270° D.315°
8.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
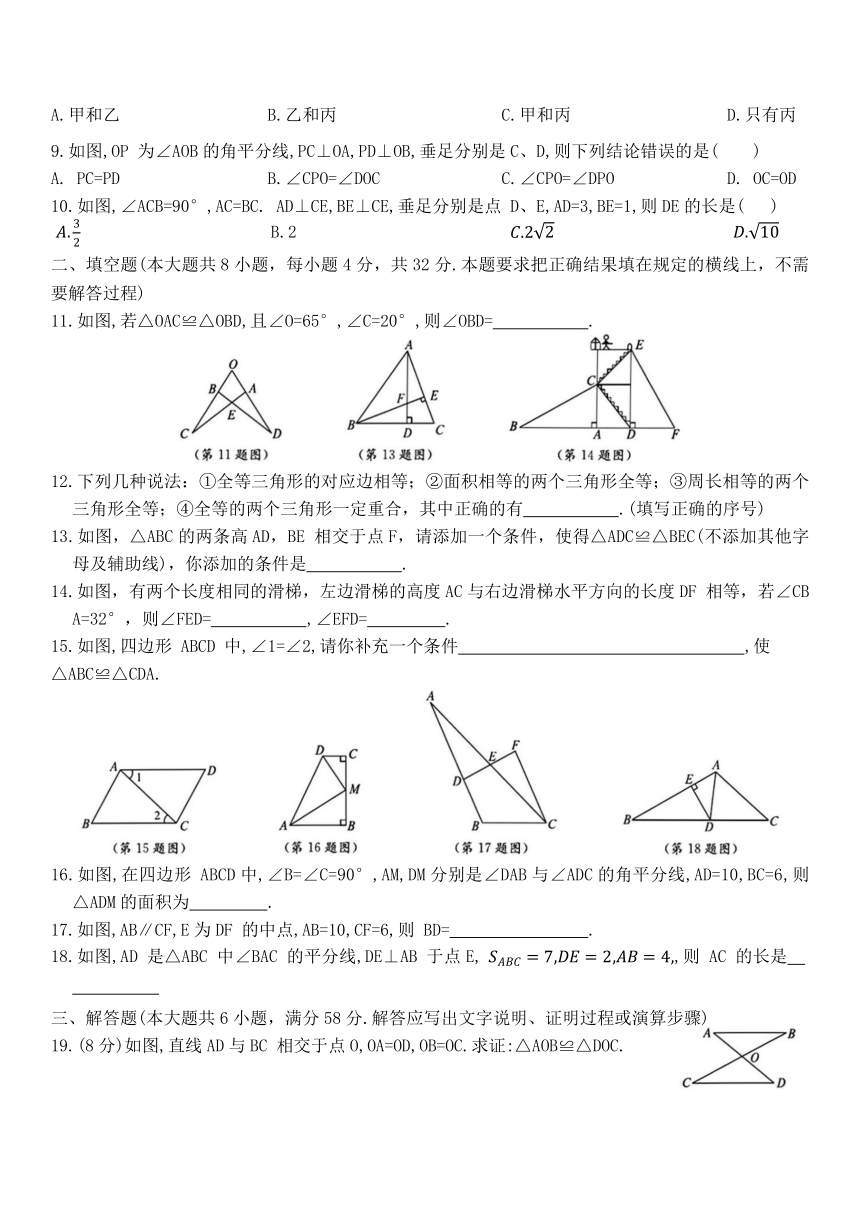
9.如图,OP 为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A. PC=PD B.∠CPO=∠DOC C.∠CPO=∠DPO D. OC=OD
10.如图,∠ACB=90°,AC=BC. AD⊥CE,BE⊥CE,垂足分别是点 D、E,AD=3,BE=1,则DE的长是( )
B.2
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.如图,若△OAC≌△OBD,且∠O=65°,∠C=20°,则∠OBD= .
12.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形一定重合,其中正确的有 .(填写正确的序号)
13.如图,△ABC的两条高AD,BE 相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
14.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF 相等,若∠CBA=32°,则∠FED= ,∠EFD= .
15.如图,四边形 ABCD 中,∠1=∠2,请你补充一个条件 ,使
△ABC≌△CDA.
16.如图,在四边形 ABCD中,∠B=∠C=90°,AM,DM分别是∠DAB与∠ADC的角平分线,AD=10,BC=6,则△ADM的面积为 .
17.如图,AB∥CF,E为DF 的中点,AB=10,CF=6,则 BD= .
18.如图,AD 是△ABC 中∠BAC 的平分线,DE⊥AB 于点E, ,则 AC 的长是
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)如图,直线AD与BC 相交于点O,OA=OD,OB=OC.求证:△AOB≌△DOC.
20.(9分)如图,已知AC平分 求证:
21.(9分)如图1,在一次军事演习中,红方侦察员发现蓝方指挥部在A 区内,到铁路到公路的距离相等,且离铁路与公路交叉处点 B 700米,如果你是红方的指挥员,请你在图2所示的作战图上标出蓝方指挥部的位置,并简要说明理由.
22.(10分)如图, 和 的顶点C,E,F,B在同一直线上,点 A,点 D 在BC 两侧,已知
与 全等吗 说明理由.
(2)CE 与BF 相等吗 为什么
23.(10 分)如图,已知. 与 的面积相等,判断 OP 是否平分 ,并说明理由.
24.(12分)如图,小强在河的一边,要测河面的一只船B与对岸码头A 的距离,他的做法如下:
①在岸边确定一点 C,使C与A,B 在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画 使F、O、A 在同一直线上;
④在线段 DF 上找一点E,使 E与O、B 共线.
他说测出线段EF的长就是船B 与码头A 的距离.他这样做有道理吗 为什么
第 12 章测试卷
1. C 2. C 3. D 4. C 5. C 6. D 7. A 8. D 9. B 10. B11.95° 12.①④ 13. AC=BC 14.32° 58°
15. AD=BC(或∠B=∠D或AB∥CD)
16.15 17.4 18.3
19.证明 在△AOB 和△DOC中,∵OA=OD,∠AOB=∠DOC,OB=OC,
∴△AOB≌△DOC(SAS).
20.证明∵AC平分∠BAD,∴∠BAC=∠DAC,在△ABC和△ADC中
∴△ABC≌△ADC(SAS).
21.解∵蓝方指挥部在A区内且到铁路到公路的距离相等,∴蓝方指挥部在两条路所成夹角的平分线上,由比例尺算出到点 B的距离为3.5cm .
22.解(1)△ABE≌△DCF.理由如下:
∵AB∥CD,∴∠B=∠C.在△ABE和△DCF中,
(2)相等,理由如下:由(1)得△ABE≌△DCF,
∴BE=CF.∴BE-EF=CF-EF,即CE=BF.23.解OP平分∠AOD.理由如下:过P点作PM⊥AB,PN⊥CD,垂足分别是M,N 两点.
∵AB=CD,△PAB与△PCD的面积相等,
∴PM=PN.∴点P到OA,OD的距离相等.
∴OP平分∠AOD(到角的两边距离相等的点在角的平分线上).
24.解 有道理,∵DF⊥CD,AC⊥CD,
∴∠C=∠D=90°,
∵O为CD中点,∴CO=DO,
在△ACO和△FDO中
∴△ACO≌△FDO(ASA),
∴AO=FO,∠A=∠F,
在△ABO和△EOF 中
∴△ABO≌△FEO(ASA),∴EF=AB.
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.如图,在下列4个正方形图案中,与左边正方形图案全等的图案是( )
2.如图,已知△ACE≌△DBF,下列结论中正确的个数是( )
①AC=DB;②AB=DC;③∠1=∠2;④AE∥DF;⑤S△NCE=S△DFB;⑥BC=AE;⑦BF∥EC.
A.4 B.5 C.6 D.7
3.如图,点 D,E分别在线段AB,AC上,CD与BE 相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B. AD=AE C. BD=CE D. BE=CD
4.如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
A. SSS B. SAS C. HL D. AAS
5.已知OP 是∠AOB 的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )
A. PN<3 B. PN>3 C. PN≥3 D. PN≤3
6.如图,在四边形ABCD 中,E是BC 的中点,连接AC,AE,若AB=AC,AE=CD,AD=CE,则图中的全等三角形有( )
A.0对 B.1对 C.2对 D.3对
7.如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于( )
A.585° B.540° C.270° D.315°
8.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
9.如图,OP 为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A. PC=PD B.∠CPO=∠DOC C.∠CPO=∠DPO D. OC=OD
10.如图,∠ACB=90°,AC=BC. AD⊥CE,BE⊥CE,垂足分别是点 D、E,AD=3,BE=1,则DE的长是( )
B.2
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.如图,若△OAC≌△OBD,且∠O=65°,∠C=20°,则∠OBD= .
12.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形一定重合,其中正确的有 .(填写正确的序号)
13.如图,△ABC的两条高AD,BE 相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
14.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF 相等,若∠CBA=32°,则∠FED= ,∠EFD= .
15.如图,四边形 ABCD 中,∠1=∠2,请你补充一个条件 ,使
△ABC≌△CDA.
16.如图,在四边形 ABCD中,∠B=∠C=90°,AM,DM分别是∠DAB与∠ADC的角平分线,AD=10,BC=6,则△ADM的面积为 .
17.如图,AB∥CF,E为DF 的中点,AB=10,CF=6,则 BD= .
18.如图,AD 是△ABC 中∠BAC 的平分线,DE⊥AB 于点E, ,则 AC 的长是
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)如图,直线AD与BC 相交于点O,OA=OD,OB=OC.求证:△AOB≌△DOC.
20.(9分)如图,已知AC平分 求证:
21.(9分)如图1,在一次军事演习中,红方侦察员发现蓝方指挥部在A 区内,到铁路到公路的距离相等,且离铁路与公路交叉处点 B 700米,如果你是红方的指挥员,请你在图2所示的作战图上标出蓝方指挥部的位置,并简要说明理由.
22.(10分)如图, 和 的顶点C,E,F,B在同一直线上,点 A,点 D 在BC 两侧,已知
与 全等吗 说明理由.
(2)CE 与BF 相等吗 为什么
23.(10 分)如图,已知. 与 的面积相等,判断 OP 是否平分 ,并说明理由.
24.(12分)如图,小强在河的一边,要测河面的一只船B与对岸码头A 的距离,他的做法如下:
①在岸边确定一点 C,使C与A,B 在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画 使F、O、A 在同一直线上;
④在线段 DF 上找一点E,使 E与O、B 共线.
他说测出线段EF的长就是船B 与码头A 的距离.他这样做有道理吗 为什么
第 12 章测试卷
1. C 2. C 3. D 4. C 5. C 6. D 7. A 8. D 9. B 10. B11.95° 12.①④ 13. AC=BC 14.32° 58°
15. AD=BC(或∠B=∠D或AB∥CD)
16.15 17.4 18.3
19.证明 在△AOB 和△DOC中,∵OA=OD,∠AOB=∠DOC,OB=OC,
∴△AOB≌△DOC(SAS).
20.证明∵AC平分∠BAD,∴∠BAC=∠DAC,在△ABC和△ADC中
∴△ABC≌△ADC(SAS).
21.解∵蓝方指挥部在A区内且到铁路到公路的距离相等,∴蓝方指挥部在两条路所成夹角的平分线上,由比例尺算出到点 B的距离为3.5cm .
22.解(1)△ABE≌△DCF.理由如下:
∵AB∥CD,∴∠B=∠C.在△ABE和△DCF中,
(2)相等,理由如下:由(1)得△ABE≌△DCF,
∴BE=CF.∴BE-EF=CF-EF,即CE=BF.23.解OP平分∠AOD.理由如下:过P点作PM⊥AB,PN⊥CD,垂足分别是M,N 两点.
∵AB=CD,△PAB与△PCD的面积相等,
∴PM=PN.∴点P到OA,OD的距离相等.
∴OP平分∠AOD(到角的两边距离相等的点在角的平分线上).
24.解 有道理,∵DF⊥CD,AC⊥CD,
∴∠C=∠D=90°,
∵O为CD中点,∴CO=DO,
在△ACO和△FDO中
∴△ACO≌△FDO(ASA),
∴AO=FO,∠A=∠F,
在△ABO和△EOF 中
∴△ABO≌△FEO(ASA),∴EF=AB.
