华师大版数学八年级下册 第17 章函数及其图象 单元测试卷(含答案)
文档属性
| 名称 | 华师大版数学八年级下册 第17 章函数及其图象 单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 646.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 09:58:19 | ||
图片预览

文档简介
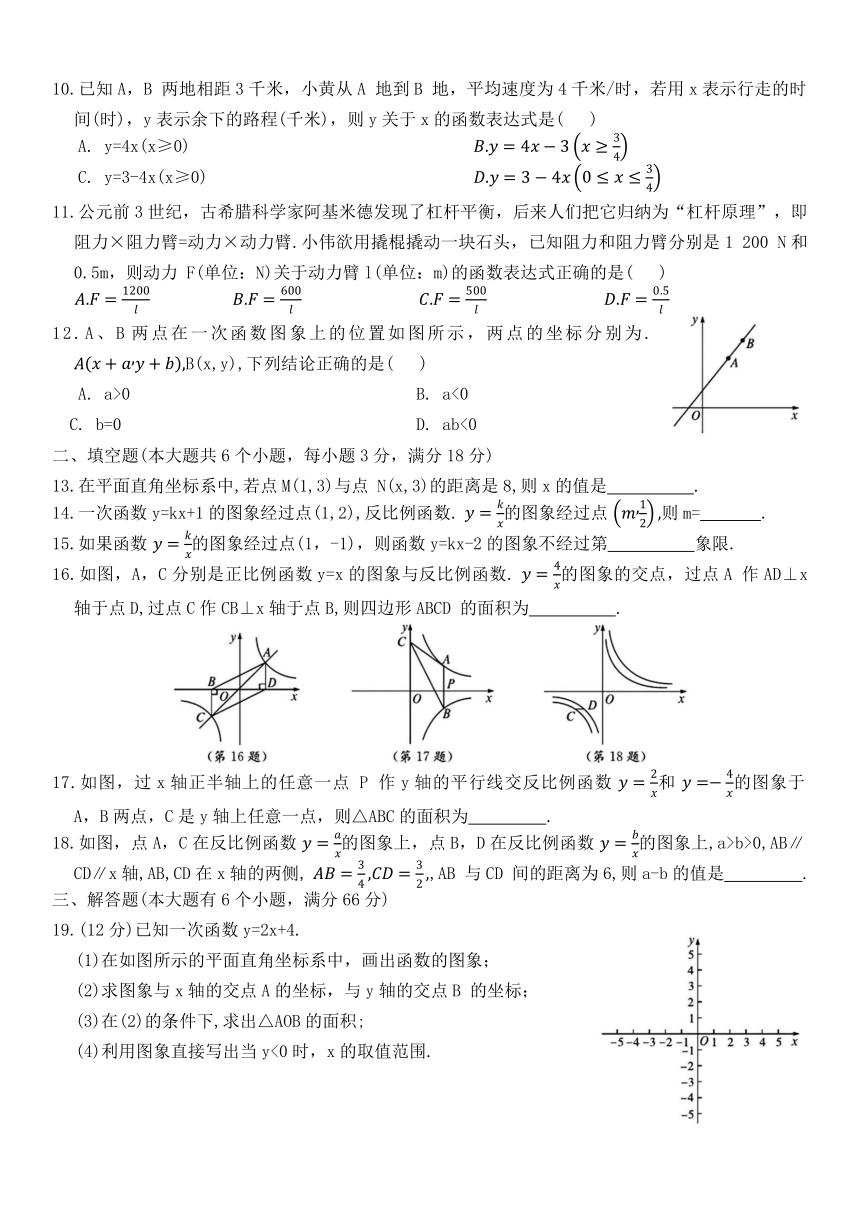
第17 章测试卷
(时间:90分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(本大题共12小题,每小题3分,满分36分)
1.小军用50元钱买单价为8元的笔记本,他剩余的钱数Q(元)与他买这种笔记本的本数x之间的关系式为Q=50-8x,则下列说法正确的是( )
A. Q和x是变量 B. Q是自变量 C.50和x是常量 D. x是Q的函数
2.函数 中,自变量x的取值范围是( )
A. x>0 B. x≥0 C. x<0 D. x≤0
3.下面说法错误的是( )
A.点(0,-2)在 y轴的负半轴上 B.点(3,2)与(3,-2)关于x轴对称
C.点(-4,-3)关于原点的对称点是(4,3) D.点在第二象限
4.如图,函数y=k(x-10)和函数 (其中k是不等于0的常数)在同一平面直角坐标系中的大致图象可能为( )
A.①③ B.①④ C.②③ D.②④
5.下列图形中,阴影部分的面积相等的是( )
A.①② B.②③ C.③④ D.①④
6.在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点.设k为整数,当直线y=x-2与y=kx+k的交点为整点时,k的值可以取( )
A.4个 B.5个 C.6个 D.7个
7.已知一次函数y=x+2与y=-2+x,下面说法正确的是( )
A.两直线交于点(1,0) B.两直线之间的距离为4个单位
C.两直线与x轴的夹角都是 30° D.两条已知直线与直线y=x都平行
8.一次函数 与反比例函数 的图象如图所示,当yA. x<2 B. x>5
C.25
9.已知关于x、y的函数 是反比例函数,则m的值为( )
A.3 B. -3 C.±3 D.0
10.已知A,B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/时,若用x表示行走的时间(时),y表示余下的路程(千米),则y关于x的函数表达式是( )
A. y=4x(x≥0)
C. y=3-4x(x≥0)
11.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1 200 N和0.5m,则动力 F(单位:N)关于动力臂l(单位:m)的函数表达式正确的是( )
12.A、B两点在一次函数图象上的位置如图所示,两点的坐标分别为. B(x,y),下列结论正确的是( )
A. a>0 B. a<0
C. b=0 D. ab<0
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.在平面直角坐标系中,若点M(1,3)与点 N(x,3)的距离是8,则x的值是 .
14.一次函数y=kx+1的图象经过点(1,2),反比例函数. 的图象经过点 则m= .
15.如果函数 的图象经过点(1,-1),则函数y=kx-2的图象不经过第 象限.
16.如图,A,C分别是正比例函数y=x的图象与反比例函数. 的图象的交点,过点A 作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD 的面积为 .
17.如图,过x轴正半轴上的任意一点 P 作y轴的平行线交反比例函数 和 的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为 .
18.如图,点A,C在反比例函数 的图象上,点B,D在反比例函数 的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧, ,AB 与CD 间的距离为6,则a-b的值是 .
三、解答题(本大题有6个小题,满分66分)
19.(12分)已知一次函数y=2x+4.
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴的交点B 的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出当y<0时,x的取值范围.
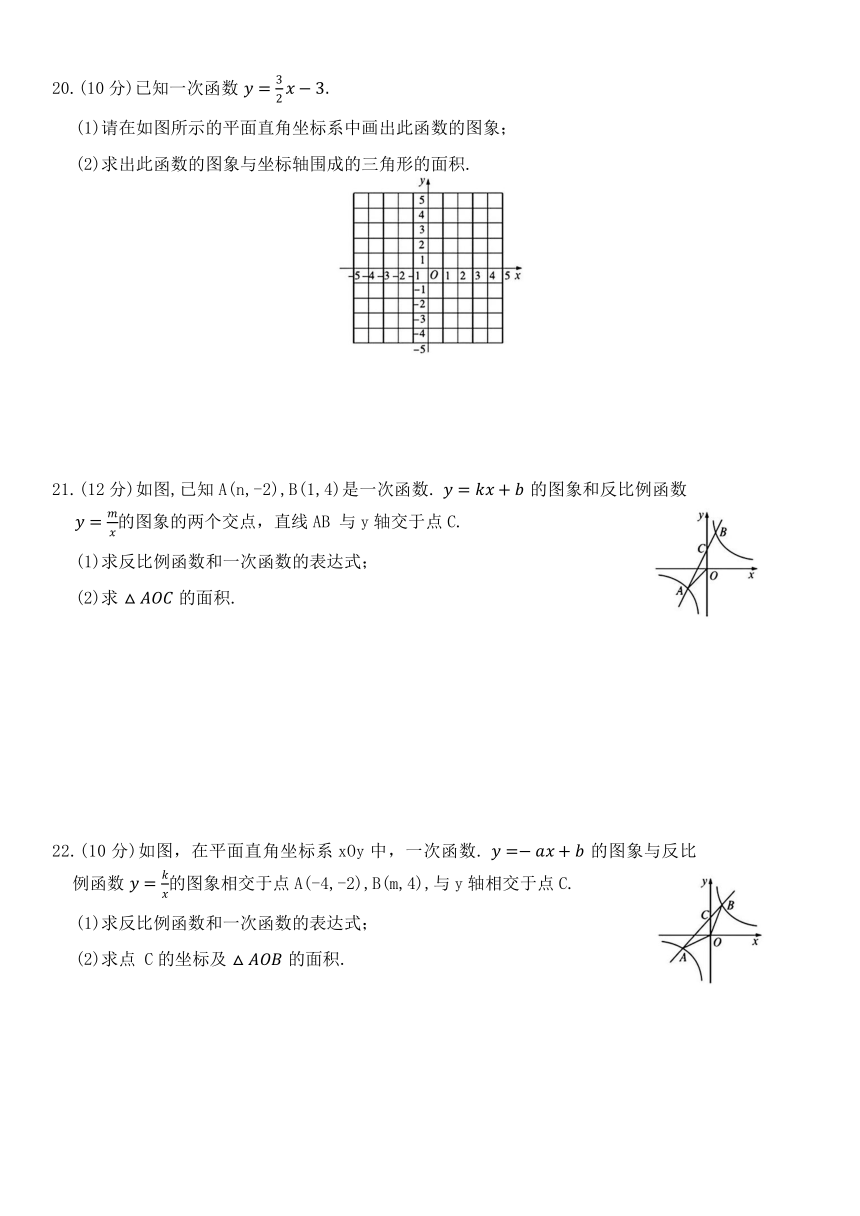
20.(10分)已知一次函数
(1)请在如图所示的平面直角坐标系中画出此函数的图象;
(2)求出此函数的图象与坐标轴围成的三角形的面积.
21.(12分)如图,已知A(n,-2),B(1,4)是一次函数. 的图象和反比例函数 的图象的两个交点,直线AB 与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求 的面积.
22.(10分)如图,在平面直角坐标系xOy中,一次函数. 的图象与反比例函数 的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求点 C的坐标及 的面积.
23.(10分)某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶路程超过3千米的部分,按每千米1.6 元计费.
(1)求出租车收费y(元)与行驶路程x(千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.4元,求他这次乘坐了多少千米的路程.
24.(12 分)如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为35 千瓦时时汽车已行驶的路程;当( 时,求1千瓦时的电量汽车能行驶的路程.
(2)当 时,求 y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
第17 章测试卷
1. A 2. B 3. D 4. C 5. C 6. A 7. D 8. D 9. A10. D 11. B 12. B
13.9或一7 14.2 15.一 16.8 17.3 18.3
19.解(1)当x=0时,y=4;当y=0时,x=-2.图象如图所示.
(2)由(1)知,A(-2,0)、B(0,4).
(4)当y<0时,x的取值范围为x<-2.
20.解(1)函数图象如图所示:
(2)函数的图象与坐标轴围成的三角形的面积为 3=3.
21.解(1)将B(1,4)的坐标代入 中,得m=4,所以
将A(n,-2)的坐标代入 中,得n=-2.
将A(-2,-2),B(1,4)的坐标分别代入y=kx+b中,得 解得
所以y=2x+2.
(2)对于y=2x+2,令x=0,则y=2,所以OC=2,所以
22.解(1)∵点A(-4,-2)在反比例函数 的图象上,∴k=-4×(-2)=8,
∴反比例函数的表达式为
∵点B(m,4)在反比例函数 的图象上,
∴4m=8,解得m=2,
∴点B(2,4).
将A(-4,-2),B(2,4)代入y=-ax+b,得
解得
∴一次函数的表达式为y=x+2.
(2)令x=0,则y=x+2=2,∴点C的坐标为(0,2),
23.解(1)∵当0又∵当 时,行驶路程超过3千米的部分是( 千米,
综上:出租车收费y(元)与行驶路程x(千米)的函数关系式是
(2)∵14.4元>8元,∴乘车路程超过3千米,
由(1)得: 解得
答:当付车费14.4元时,乘车路程为7千米.
24.解(1)由图象可知,蓄电池剩余电量为 35 千瓦时时汽车已行驶了 150千米.1千瓦时的电量汽车能行驶的路程为 (千米).
(2)设 把点(150,35),(200,10)代入,得
当 时,
答:当 时,y关于x 的函数表达式为. 当汽车已行驶 180 千米时,蓄电池的剩余电量为20千瓦时.
(时间:90分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(本大题共12小题,每小题3分,满分36分)
1.小军用50元钱买单价为8元的笔记本,他剩余的钱数Q(元)与他买这种笔记本的本数x之间的关系式为Q=50-8x,则下列说法正确的是( )
A. Q和x是变量 B. Q是自变量 C.50和x是常量 D. x是Q的函数
2.函数 中,自变量x的取值范围是( )
A. x>0 B. x≥0 C. x<0 D. x≤0
3.下面说法错误的是( )
A.点(0,-2)在 y轴的负半轴上 B.点(3,2)与(3,-2)关于x轴对称
C.点(-4,-3)关于原点的对称点是(4,3) D.点在第二象限
4.如图,函数y=k(x-10)和函数 (其中k是不等于0的常数)在同一平面直角坐标系中的大致图象可能为( )
A.①③ B.①④ C.②③ D.②④
5.下列图形中,阴影部分的面积相等的是( )
A.①② B.②③ C.③④ D.①④
6.在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点.设k为整数,当直线y=x-2与y=kx+k的交点为整点时,k的值可以取( )
A.4个 B.5个 C.6个 D.7个
7.已知一次函数y=x+2与y=-2+x,下面说法正确的是( )
A.两直线交于点(1,0) B.两直线之间的距离为4个单位
C.两直线与x轴的夹角都是 30° D.两条已知直线与直线y=x都平行
8.一次函数 与反比例函数 的图象如图所示,当y
C.2
9.已知关于x、y的函数 是反比例函数,则m的值为( )
A.3 B. -3 C.±3 D.0
10.已知A,B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/时,若用x表示行走的时间(时),y表示余下的路程(千米),则y关于x的函数表达式是( )
A. y=4x(x≥0)
C. y=3-4x(x≥0)
11.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1 200 N和0.5m,则动力 F(单位:N)关于动力臂l(单位:m)的函数表达式正确的是( )
12.A、B两点在一次函数图象上的位置如图所示,两点的坐标分别为. B(x,y),下列结论正确的是( )
A. a>0 B. a<0
C. b=0 D. ab<0
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.在平面直角坐标系中,若点M(1,3)与点 N(x,3)的距离是8,则x的值是 .
14.一次函数y=kx+1的图象经过点(1,2),反比例函数. 的图象经过点 则m= .
15.如果函数 的图象经过点(1,-1),则函数y=kx-2的图象不经过第 象限.
16.如图,A,C分别是正比例函数y=x的图象与反比例函数. 的图象的交点,过点A 作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD 的面积为 .
17.如图,过x轴正半轴上的任意一点 P 作y轴的平行线交反比例函数 和 的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为 .
18.如图,点A,C在反比例函数 的图象上,点B,D在反比例函数 的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧, ,AB 与CD 间的距离为6,则a-b的值是 .
三、解答题(本大题有6个小题,满分66分)
19.(12分)已知一次函数y=2x+4.
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴的交点B 的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出当y<0时,x的取值范围.
20.(10分)已知一次函数
(1)请在如图所示的平面直角坐标系中画出此函数的图象;
(2)求出此函数的图象与坐标轴围成的三角形的面积.
21.(12分)如图,已知A(n,-2),B(1,4)是一次函数. 的图象和反比例函数 的图象的两个交点,直线AB 与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求 的面积.
22.(10分)如图,在平面直角坐标系xOy中,一次函数. 的图象与反比例函数 的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求点 C的坐标及 的面积.
23.(10分)某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶路程超过3千米的部分,按每千米1.6 元计费.
(1)求出租车收费y(元)与行驶路程x(千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.4元,求他这次乘坐了多少千米的路程.
24.(12 分)如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为35 千瓦时时汽车已行驶的路程;当( 时,求1千瓦时的电量汽车能行驶的路程.
(2)当 时,求 y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
第17 章测试卷
1. A 2. B 3. D 4. C 5. C 6. A 7. D 8. D 9. A10. D 11. B 12. B
13.9或一7 14.2 15.一 16.8 17.3 18.3
19.解(1)当x=0时,y=4;当y=0时,x=-2.图象如图所示.
(2)由(1)知,A(-2,0)、B(0,4).
(4)当y<0时,x的取值范围为x<-2.
20.解(1)函数图象如图所示:
(2)函数的图象与坐标轴围成的三角形的面积为 3=3.
21.解(1)将B(1,4)的坐标代入 中,得m=4,所以
将A(n,-2)的坐标代入 中,得n=-2.
将A(-2,-2),B(1,4)的坐标分别代入y=kx+b中,得 解得
所以y=2x+2.
(2)对于y=2x+2,令x=0,则y=2,所以OC=2,所以
22.解(1)∵点A(-4,-2)在反比例函数 的图象上,∴k=-4×(-2)=8,
∴反比例函数的表达式为
∵点B(m,4)在反比例函数 的图象上,
∴4m=8,解得m=2,
∴点B(2,4).
将A(-4,-2),B(2,4)代入y=-ax+b,得
解得
∴一次函数的表达式为y=x+2.
(2)令x=0,则y=x+2=2,∴点C的坐标为(0,2),
23.解(1)∵当0
综上:出租车收费y(元)与行驶路程x(千米)的函数关系式是
(2)∵14.4元>8元,∴乘车路程超过3千米,
由(1)得: 解得
答:当付车费14.4元时,乘车路程为7千米.
24.解(1)由图象可知,蓄电池剩余电量为 35 千瓦时时汽车已行驶了 150千米.1千瓦时的电量汽车能行驶的路程为 (千米).
(2)设 把点(150,35),(200,10)代入,得
当 时,
答:当 时,y关于x 的函数表达式为. 当汽车已行驶 180 千米时,蓄电池的剩余电量为20千瓦时.
