数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共35张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 14:35:31 | ||
图片预览









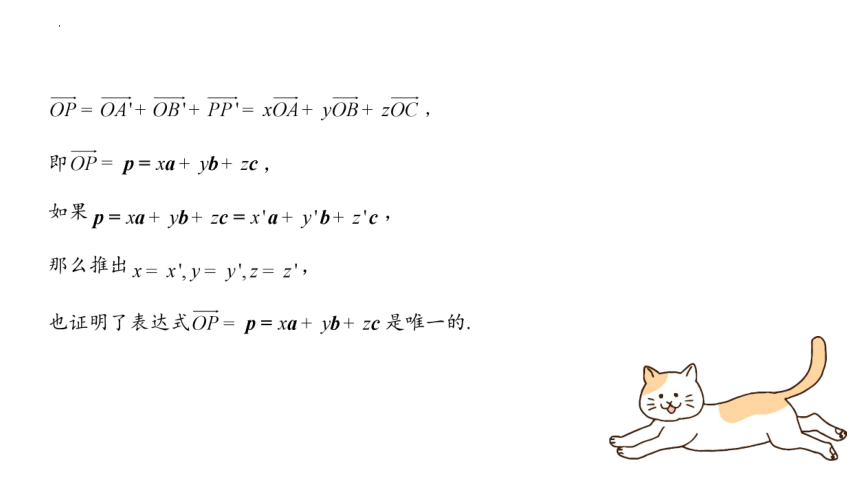
文档简介
(共35张PPT)
1.2 空间向量基本定理
学习目标
1.了解空间向量基本定理的意义
2.理解空间任一向量都可用空间不共面三个已知向量唯一线性表示
3.会用选取空间三个不共面向量作为基底表示其他向量
4.会用空间向量基本定理证明平行、垂直问题和求夹角
学习难点
学习重点
空间向量基本定理
对空间向量基本定理的理解和应用
新课导入
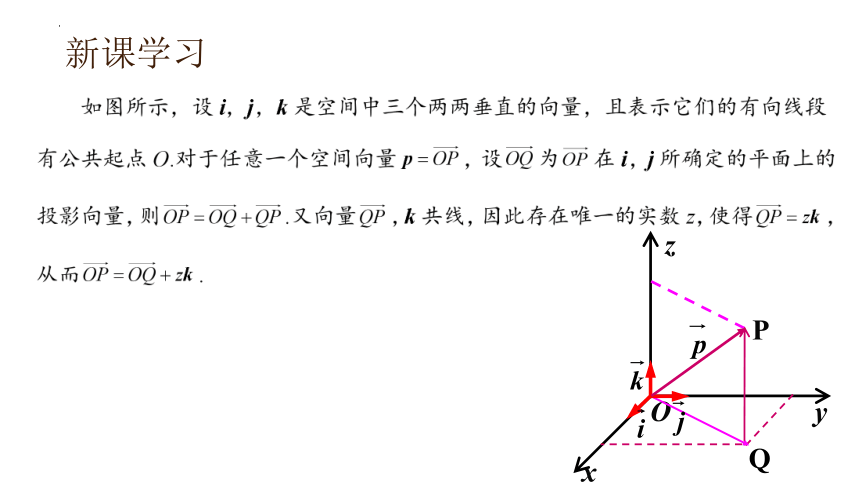
新课学习
x
y
z
O
Q
P
结论
唯一的
证明:
探究一下
在空间中,如果用任意三个不共面的向量a,b,c代替两两垂直的向量i,j,k,你能得出类似的结论吗?
类似平面基本定理,我们可以得到空间向量基本定理
空间向量基本定理
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
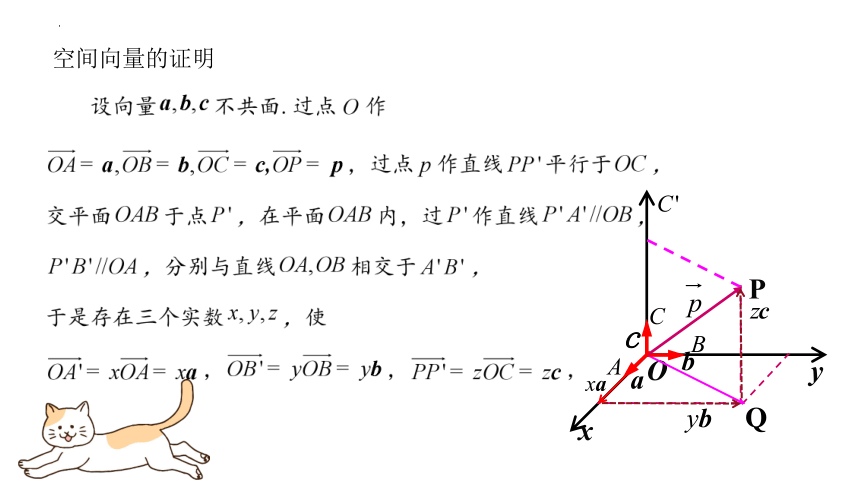
空间向量的证明
x
y
O
Q
P
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
推论:
1.判断由三个向量组成的向量组能否作为基底,关键是判断这三个向量是否共面,首先考虑三个向量是不是零向量,其次判断三个非零向量是否共面.如果从正面入手难以判断三个向量是否共面,可假设三个向量共面,利用向量共面的充要条件建立方程组,若方程组有解,则三个向量共面;若方程组无解,则三个向量不共面.
例题来了
A
B
C
M
N
P
O
解:
A
B
C
M
N
P
O
A
B
C
D
M
N
B1
A1
C1
D1
证明:
A′
B′
C′
D′
A
B
C
D
G
E
F
O
A′
B′
C′
D′
A
B
C
D
G
E
F
O
解:
课堂巩固
C
B
D
A
B
C
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
B
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
总结一下
1.空间向量基本定理
2.基底和基向量
3.空间向量的正交分解
感谢观看
1.2 空间向量基本定理
学习目标
1.了解空间向量基本定理的意义
2.理解空间任一向量都可用空间不共面三个已知向量唯一线性表示
3.会用选取空间三个不共面向量作为基底表示其他向量
4.会用空间向量基本定理证明平行、垂直问题和求夹角
学习难点
学习重点
空间向量基本定理
对空间向量基本定理的理解和应用
新课导入
新课学习
x
y
z
O
Q
P
结论
唯一的
证明:
探究一下
在空间中,如果用任意三个不共面的向量a,b,c代替两两垂直的向量i,j,k,你能得出类似的结论吗?
类似平面基本定理,我们可以得到空间向量基本定理
空间向量基本定理
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
空间向量的证明
x
y
O
Q
P
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
推论:
1.判断由三个向量组成的向量组能否作为基底,关键是判断这三个向量是否共面,首先考虑三个向量是不是零向量,其次判断三个非零向量是否共面.如果从正面入手难以判断三个向量是否共面,可假设三个向量共面,利用向量共面的充要条件建立方程组,若方程组有解,则三个向量共面;若方程组无解,则三个向量不共面.
例题来了
A
B
C
M
N
P
O
解:
A
B
C
M
N
P
O
A
B
C
D
M
N
B1
A1
C1
D1
证明:
A′
B′
C′
D′
A
B
C
D
G
E
F
O
A′
B′
C′
D′
A
B
C
D
G
E
F
O
解:
课堂巩固
C
B
D
A
B
C
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
B
输入标题
请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。请在此处点击,更换你需要的内容。
总结一下
1.空间向量基本定理
2.基底和基向量
3.空间向量的正交分解
感谢观看
