北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题(图片版,含答案)
文档属性
| 名称 | 北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题(图片版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 00:00:00 | ||
图片预览




文档简介
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
高一下数学统练 4
2024年 7月
姓名:___________班级:___________考号:___________
一、单选题(共 10题,每题 4分,共 40分)
1. 已知向量a,b满足a = (2,1) ,a b = ( 1,2),则a b =( )
A. 5 B. 0 C. 5 D. 7
【答案】C
2. A, B是圆心为O的单位圆上两个动点,当 AOB 面积最大时,则下列判断错误的是
A. AB = 2 B. AB 的长为 C. 扇形 AOB的面积为 D. AOB 等边三角形
2 4
【答案】D
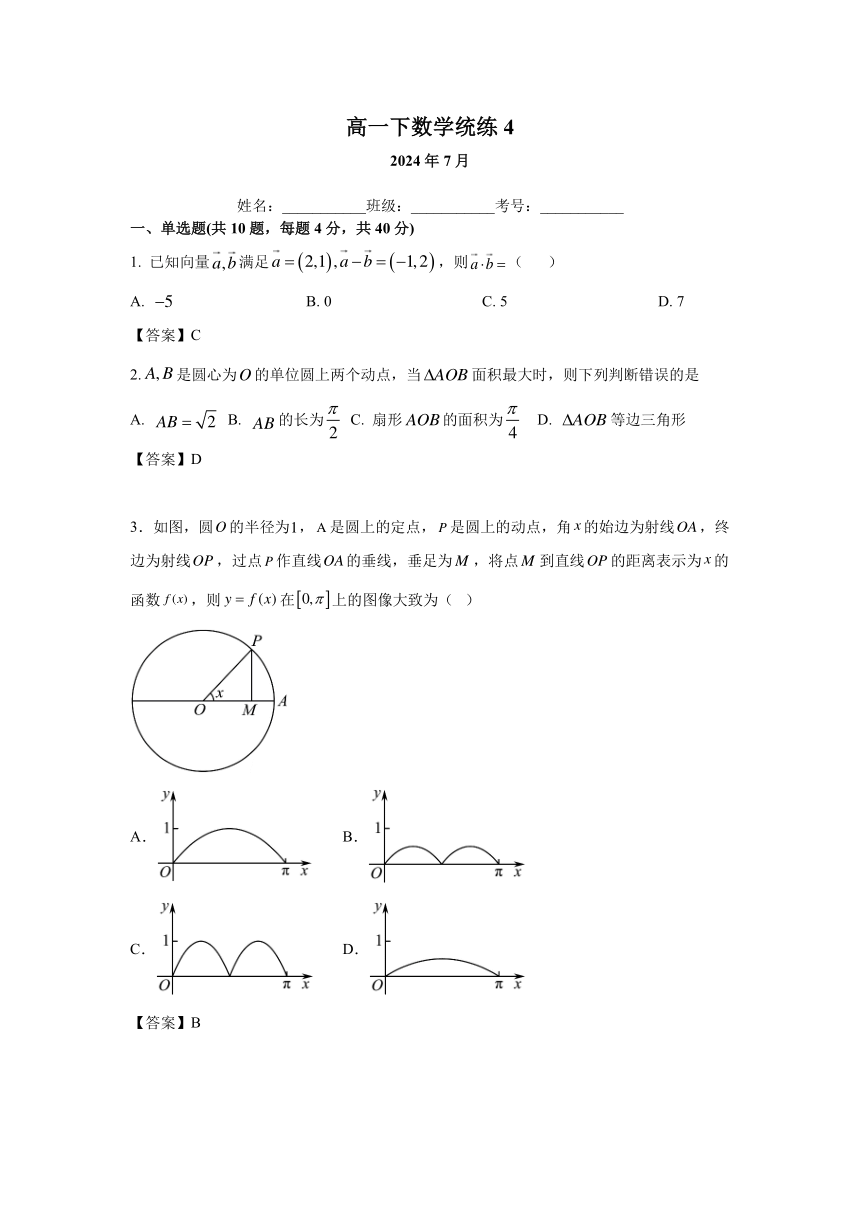
3.如图,圆O的半径为1,A 是圆上的定点, P 是圆上的动点,角 x的始边为射线OA,终
边为射线OP ,过点 P 作直线OA的垂线,垂足为M ,将点M 到直线OP 的距离表示为 x的
函数 f (x) ,则 y = f (x) 在 0, 上的图像大致为( )
A. B.
C. D.
【答案】B
{#{QQABBAYSQhA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
【详解】
如图:过M 作MD ⊥OP于D,则由题意可得:PM = sin x,OM = cos x ,
1
在Rt△OMP中, S OMP = MD OP =OM PM ,
2
OM PM cos x sin x 1
所以MD = = = cos xsin x = sin 2x ,
OP 1 2
1
∴ f (x) = sin 2x (0 x ) .
2
故选:B.
4.将函数 f (x) = sin 2x 的图象向左平移 个单位后得到函数 g(x)的图象,若函数
y = f (x) + g(x) 的最大值为a,则a的值不可能为( )
A.1 B. 2 1
C.2 D. 2 +1
【答案】D
【详解】由题意得 g (x) = sin (2x + 2 ),
则 y = f (x)+ g (x) = sin 2x + sin (2x + 2 )
= sin 2x + cos 2 sin 2x + sin 2 cos 2x
= (1+ cos 2 )sin 2x + sin 2 cos 2x
2
= (1+ cos 2 ) + sin2 2 sin (2x + )
= 2+ 2cos 2 sin (2x + ),,
因为cos 2 1,1 ,所以 2+ 2cos 2 0,2 ,所以a 0,2 .
故选:D.
5. “sin + tan 0”是“ 为第一或第三象限角”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
【答案】C
6.关于函数 f (x) = sin x + cos2x ,给出下列三个命题:
π
① f (x) 是周期函数;② 曲线 y = f (x) 关于直线 x = 对称;
2
③ f (x) 在区间[0,2π ) 上恰有3个零点.④ f (x) 最小值为 2
其中真命题的个数为
A. 1 B. 2 C. 3 D. 4
【答案】D
7. 在 ABC 中,sin B = sin 2A,c = 2a ,则( )
A. B为直角 B. B为钝角 C. C 为直角 D. C 为钝角
【答案】C
【解析】
b
【详解】由sin B = sin 2A = 2sin Acos A,即b = 2a cos A,cos A = ,
2a
b2 + c2 a2 b2 + 4a2 a2 b
又 c = 2a ,所以cos A = = = ,化简得b = 3a,
2bc 2b 2a 2a
π π π
则a :b :c =1: 3 : 2,故在 ABC 中, A = , B = ,C = ,
6 3 2
故选:C
8. 在 ABC中,AB = AC =1,D 是 AC 边的中点,则 BD CD 的取值范围是( )
3 1 1 3 1 3
(A) ( , ) (B) ( , ) (C) ( ,+ ) (D) ( , )
4 4 4 4 4 4
【答案】:A
3 x 1
9.已知 f (x) = sin x + sin2 ( 0),则下列说法错误的是( )
2 2 2
2
A.若 f (x)在 (0, )内单调,则0
3
1
B.若 f (x)在 (0, )内无零点,则0
6
C.若 y = f (x) 的最小正周期为 ,则 = 2
{#{QQABABYSQhA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
2π
D.若 = 2时,直线 x = 是函数 f (x)图象的一条对称轴
3
【答案】C
3 x 1 3 1
【详解】由题意,函数 f (x) = sin x + sin2 = sin x cos x = sin( x ),
2 2 2 2 2 6
对于 A 中,由 x (0, ),可得 x ( , ) ,
6 6 6
2
要使得 f (x)在 (0, )内单调,则满足 ,解得 ,
6 2 3
2
因为 0,所以0 ,所以 A 正确;
3
对于 B 中,由 x (0, ),可得 x ( , ) ,
6 6 6
1
要使得 f (x)在 (0, )内无零点,则 0,解得 ,
6 6
1
因为 0,所以0 ,所以 B 正确;
6
对于 C 中,函数 y = f (x) 的最小正周期为 ,可得 = ,解得 =1,所以 C 不正确;
对于 D 中,若 = 2,则函数 f (x) = sin(2x ),
6
2 3 2
当 x = 时,2x = ,此时 f ( ) =1,
3 6 2 3
2
则直线 x = 是函数 f (x)图象的一条对称轴,所以 D 正确.
3
故选:C.
10.在 ABC中, BAC = 90 ,BC = 2, 点P 在BC 边上,且 AP (AB + AC ) =1,则
AP 的取值范围是
1 1 2 2
(A) ( , 1] (B)[ ,1] (C) ( ,1] (D)[ ,1]
2 2 2 2
【答案】:A
【详解】以BC 的中点为原点,过O垂直于BC 的直线为 y 轴,BC 为 x轴,
建立平面直角坐标系,如图:
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
则B ( 1,0), (1,0),
设P (x,0), A(a,b), x 1,
OA =1, a2 +b2 =1,
则由 AP ( 1AB + AC ) =1,得 (x a, b) ( a, b) = ,
2
1
化简ax = ,
2
2 2
所以 AP = (x a) + b2 = x2 2ax + a2 + b2 = x2 ,
由 a2 +b2 =1,因为a 1,所以 a 1,
1 1
所以 x = ,
2a 2
1
所以 AP = x 的取值范围为 ,1 .
2
故选:A
二.填空题(共 5题,每题 5 分,共 25分)
11.若 z (1+ i) = 2+3i,( z C ) . z 的虚部______
5 2+3i 1+5i
【答案】: , z = =
2 1+ i 2
π
12.已知 ABC 中, A = , a = 13 ,b = 2,则c = .
6
【答案】: 3 3
13.在 ABC 中, A = 30 , AC = 2 3,满足此条件 ABC 有两解,则 BC边长度的取值
范围为 .
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
【答案】: ( 3,2 3)
10
14.已知sin + 2cos = , tan 2 = ______
2
3
【答案】: ,设OA = (2,1) ,OB = (cos ,sin ) ,OA为角 的终边
4
10 10
所以OA OB = 5 cos AOB = AOB = =
2 2 4 4
1
1
1 4 3 tan 2 = tan 2 = = =
2 tan 2 1 4
15.设 ABC 的内角 A,B,C 所对边的长分别为a,b,c
①若 A B ,则sin A sin B;
②若cos A cos B .则 A B;
③若a2 tan B = b2 tan A,则 ABC 一定为等腰直角三角形;
④若sin2 A+ cos2 C cos2 B ,则 ABC 一定为钝角三角形;
⑤若 tan A+ tan B + tan C 0,则 ABC 一定为锐角三角形.
则上述命题中正确的是________.(写出所有正确命题的编号)
【答案】①②④⑤
【详解】对于命题①②,在 ABC 中,有 A B a b sin A sin B ,
显然cos A cos B A B.
因此命题①②正确.
对于命题③,有a2 tan B = b2 tan A sin3 Acos A = sin3 Bcos B ,
记 f (x) = sin3 xcos x,则 f (0) = f = 0,
2
于是 f (x) 在 0, 上不单调,因此必然存在 f (A) = f (B) 且 A B,命题错误.
2
对于命题④,根据条件,有 sin2 A sin2 C + sin2 B 0 a2 + b2 c2 ,
因此角 C 为钝角,命题正确.
对于命题⑤,根据三角恒等式,有 tan A+ tan B + tanC = tan A tan B tanC,
于是命题正确.
故选:①②④⑤
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
三.解答题(共 3道答题,共 35分)
16.(本题 10 分)
在平面直角坐标系中,O为原点, A( 2,2) , B (3,1)
(1)BO在直线 AB 上的投影是BC ,求OC
(2)若四边形 AOBD 是以OB 为底的直角梯形,求点OD
解:(1)设OC =OB + BA = (3,1)+ ( 5,1) = (3 5 ,1+ )
12 21 25
OC BA 26 14 = 0 = OC = , -----------4 分
13 13 13
(2)四边形 AOBD 是以OB 为底的直角梯形,且OA OB = 4 0, -----6 分
AD / /OB, AD ⊥ DB,-----8 分
设 D (x, y) AD = (x + 2, y 2) , BD = (x 3, y 1)
11
x =
3y 6 = x + 2 5 x = 2
或 (舍)------10 分
(x + 2)(x 3)+ ( y 2)( y 1) = 0 17 y = 2y =
5
17.(本题 13 分)
在 ABC中, BC = 4, AC = 13 , AB =1.
(I)求 B;
(II)若 D为 BC 边上一点,再从条件①、条件②、条件③这三个条件中选择一个作为已
知,使 ABD 存在且唯一确定,求 ABD 的面积.
π
条件①: ADB = ;
4
2 2
条件②: AD = ;
3
条件③: ABD 的周长为3+ 3 .
注:如果选择的条件不符合要求,第(Ⅱ)问得 0 分;如果选择多个符合要求的条件
分别解答,按第一个解答计分.
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
解:(Ⅰ)在△ABC 中,由余弦定理得
BC2 + AB2 AC2
cos B =
2BC AB
又因为 BC = 4, AC = 13 , AB =1,
42 +12 ( 13)2 1
所以cos B = = .
2 4 1 2
π
又 B (0, π) ,所以 B = . ......................................... ...........................5 分
3
π
(II)选择条件①: ADB = .
4
AD 1
AD AB =
在△ADB 中,由正弦定理 = ,得 3 2 ,
sin B sin ADB
2 2
6
所以 AD = .
2
所以 sin BAD = sin( B + ADB)
= sin Bcos ADB +cos Bsin ADB
3 2 1 2
= +
2 2 2 2
6 + 2
= .
4
1
所以 S ABD = AB ADsin BAD .
2
1 6 6 + 2
= 1
2 2 4
3+ 3
= . ......................................................................13 分
8
选择条件③:由余弦定理 AD2 = AB2 + BD2 2AB BDcos B , AB + BD + AD = 3 3 ,
2
得 (2 + 3 BD) =1+ BD2 BD ,
解得 BD = 2,
1 1 3 3
所以 S = AB BD sin B = 1 2 = . ........................ ...............13 分 ABD
2 2 2 2
18. (本题 12 分)
π π
已知函数 f (x) = 2 sin (2x + ) 的图象上所有点向右平移 个单位长度,所得函数
2 8
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
图象关于原点对称.
(1)求 的值;
1
(2)设 g (x) = f (x) 2cos2 x + ,若 g (x)在区间 (0,m)上有且只有一个零点,求m的取值
2
范围.
π π
(1)解:将函数 f (x) = 2 sin (2x + ) 的图象上所有点向右平移 个单位长度,
2 8
π π
可得到函数 y = 2 sin 2 x + = 2 sin 2x + ,-------2 分
8 4
π π
由题意可知,函数 y = 2 sin 2x + 为奇函数,则 = kπ (k Z),
4 4
π π π
可得 = + kπ (k Z),又因为 ,则 = .----------------4 分
4 2 4
π
(2)解:由(1)可知, f (x) = 2 sin 2x + = sin 2x + cos 2x,----------6 分
4
1 1 1
则 g (x) = f (x) 2cos2 x + = sin 2x + cos 2x (1+ cos 2x)+ = sin 2x ,-------8 分
2 2 2
因为0 x m,则0 2x 2m ,
1
由 g (x) = 0,可得sin 2x = ,---------10 分
2
π 5π π 5π
因为 g (x)在区间 (0,m)上有且只有一个零点,则 2m ,解得 m .
6 6 12 12
π 5π
因此,实数m的取值范围是 , .-------------------------12 分
12 12
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
高一下数学统练 4
2024年 7月
姓名:___________班级:___________考号:___________
一、单选题(共 10题,每题 4分,共 40分)
1. 已知向量a,b满足a = (2,1) ,a b = ( 1,2),则a b =( )
A. 5 B. 0 C. 5 D. 7
【答案】C
2. A, B是圆心为O的单位圆上两个动点,当 AOB 面积最大时,则下列判断错误的是
A. AB = 2 B. AB 的长为 C. 扇形 AOB的面积为 D. AOB 等边三角形
2 4
【答案】D
3.如图,圆O的半径为1,A 是圆上的定点, P 是圆上的动点,角 x的始边为射线OA,终
边为射线OP ,过点 P 作直线OA的垂线,垂足为M ,将点M 到直线OP 的距离表示为 x的
函数 f (x) ,则 y = f (x) 在 0, 上的图像大致为( )
A. B.
C. D.
【答案】B
{#{QQABBAYSQhA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
【详解】
如图:过M 作MD ⊥OP于D,则由题意可得:PM = sin x,OM = cos x ,
1
在Rt△OMP中, S OMP = MD OP =OM PM ,
2
OM PM cos x sin x 1
所以MD = = = cos xsin x = sin 2x ,
OP 1 2
1
∴ f (x) = sin 2x (0 x ) .
2
故选:B.
4.将函数 f (x) = sin 2x 的图象向左平移 个单位后得到函数 g(x)的图象,若函数
y = f (x) + g(x) 的最大值为a,则a的值不可能为( )
A.1 B. 2 1
C.2 D. 2 +1
【答案】D
【详解】由题意得 g (x) = sin (2x + 2 ),
则 y = f (x)+ g (x) = sin 2x + sin (2x + 2 )
= sin 2x + cos 2 sin 2x + sin 2 cos 2x
= (1+ cos 2 )sin 2x + sin 2 cos 2x
2
= (1+ cos 2 ) + sin2 2 sin (2x + )
= 2+ 2cos 2 sin (2x + ),,
因为cos 2 1,1 ,所以 2+ 2cos 2 0,2 ,所以a 0,2 .
故选:D.
5. “sin + tan 0”是“ 为第一或第三象限角”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
【答案】C
6.关于函数 f (x) = sin x + cos2x ,给出下列三个命题:
π
① f (x) 是周期函数;② 曲线 y = f (x) 关于直线 x = 对称;
2
③ f (x) 在区间[0,2π ) 上恰有3个零点.④ f (x) 最小值为 2
其中真命题的个数为
A. 1 B. 2 C. 3 D. 4
【答案】D
7. 在 ABC 中,sin B = sin 2A,c = 2a ,则( )
A. B为直角 B. B为钝角 C. C 为直角 D. C 为钝角
【答案】C
【解析】
b
【详解】由sin B = sin 2A = 2sin Acos A,即b = 2a cos A,cos A = ,
2a
b2 + c2 a2 b2 + 4a2 a2 b
又 c = 2a ,所以cos A = = = ,化简得b = 3a,
2bc 2b 2a 2a
π π π
则a :b :c =1: 3 : 2,故在 ABC 中, A = , B = ,C = ,
6 3 2
故选:C
8. 在 ABC中,AB = AC =1,D 是 AC 边的中点,则 BD CD 的取值范围是( )
3 1 1 3 1 3
(A) ( , ) (B) ( , ) (C) ( ,+ ) (D) ( , )
4 4 4 4 4 4
【答案】:A
3 x 1
9.已知 f (x) = sin x + sin2 ( 0),则下列说法错误的是( )
2 2 2
2
A.若 f (x)在 (0, )内单调,则0
3
1
B.若 f (x)在 (0, )内无零点,则0
6
C.若 y = f (x) 的最小正周期为 ,则 = 2
{#{QQABABYSQhA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
2π
D.若 = 2时,直线 x = 是函数 f (x)图象的一条对称轴
3
【答案】C
3 x 1 3 1
【详解】由题意,函数 f (x) = sin x + sin2 = sin x cos x = sin( x ),
2 2 2 2 2 6
对于 A 中,由 x (0, ),可得 x ( , ) ,
6 6 6
2
要使得 f (x)在 (0, )内单调,则满足 ,解得 ,
6 2 3
2
因为 0,所以0 ,所以 A 正确;
3
对于 B 中,由 x (0, ),可得 x ( , ) ,
6 6 6
1
要使得 f (x)在 (0, )内无零点,则 0,解得 ,
6 6
1
因为 0,所以0 ,所以 B 正确;
6
对于 C 中,函数 y = f (x) 的最小正周期为 ,可得 = ,解得 =1,所以 C 不正确;
对于 D 中,若 = 2,则函数 f (x) = sin(2x ),
6
2 3 2
当 x = 时,2x = ,此时 f ( ) =1,
3 6 2 3
2
则直线 x = 是函数 f (x)图象的一条对称轴,所以 D 正确.
3
故选:C.
10.在 ABC中, BAC = 90 ,BC = 2, 点P 在BC 边上,且 AP (AB + AC ) =1,则
AP 的取值范围是
1 1 2 2
(A) ( , 1] (B)[ ,1] (C) ( ,1] (D)[ ,1]
2 2 2 2
【答案】:A
【详解】以BC 的中点为原点,过O垂直于BC 的直线为 y 轴,BC 为 x轴,
建立平面直角坐标系,如图:
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
则B ( 1,0), (1,0),
设P (x,0), A(a,b), x 1,
OA =1, a2 +b2 =1,
则由 AP ( 1AB + AC ) =1,得 (x a, b) ( a, b) = ,
2
1
化简ax = ,
2
2 2
所以 AP = (x a) + b2 = x2 2ax + a2 + b2 = x2 ,
由 a2 +b2 =1,因为a 1,所以 a 1,
1 1
所以 x = ,
2a 2
1
所以 AP = x 的取值范围为 ,1 .
2
故选:A
二.填空题(共 5题,每题 5 分,共 25分)
11.若 z (1+ i) = 2+3i,( z C ) . z 的虚部______
5 2+3i 1+5i
【答案】: , z = =
2 1+ i 2
π
12.已知 ABC 中, A = , a = 13 ,b = 2,则c = .
6
【答案】: 3 3
13.在 ABC 中, A = 30 , AC = 2 3,满足此条件 ABC 有两解,则 BC边长度的取值
范围为 .
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
【答案】: ( 3,2 3)
10
14.已知sin + 2cos = , tan 2 = ______
2
3
【答案】: ,设OA = (2,1) ,OB = (cos ,sin ) ,OA为角 的终边
4
10 10
所以OA OB = 5 cos AOB = AOB = =
2 2 4 4
1
1
1 4 3 tan 2 = tan 2 = = =
2 tan 2 1 4
15.设 ABC 的内角 A,B,C 所对边的长分别为a,b,c
①若 A B ,则sin A sin B;
②若cos A cos B .则 A B;
③若a2 tan B = b2 tan A,则 ABC 一定为等腰直角三角形;
④若sin2 A+ cos2 C cos2 B ,则 ABC 一定为钝角三角形;
⑤若 tan A+ tan B + tan C 0,则 ABC 一定为锐角三角形.
则上述命题中正确的是________.(写出所有正确命题的编号)
【答案】①②④⑤
【详解】对于命题①②,在 ABC 中,有 A B a b sin A sin B ,
显然cos A cos B A B.
因此命题①②正确.
对于命题③,有a2 tan B = b2 tan A sin3 Acos A = sin3 Bcos B ,
记 f (x) = sin3 xcos x,则 f (0) = f = 0,
2
于是 f (x) 在 0, 上不单调,因此必然存在 f (A) = f (B) 且 A B,命题错误.
2
对于命题④,根据条件,有 sin2 A sin2 C + sin2 B 0 a2 + b2 c2 ,
因此角 C 为钝角,命题正确.
对于命题⑤,根据三角恒等式,有 tan A+ tan B + tanC = tan A tan B tanC,
于是命题正确.
故选:①②④⑤
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
三.解答题(共 3道答题,共 35分)
16.(本题 10 分)
在平面直角坐标系中,O为原点, A( 2,2) , B (3,1)
(1)BO在直线 AB 上的投影是BC ,求OC
(2)若四边形 AOBD 是以OB 为底的直角梯形,求点OD
解:(1)设OC =OB + BA = (3,1)+ ( 5,1) = (3 5 ,1+ )
12 21 25
OC BA 26 14 = 0 = OC = , -----------4 分
13 13 13
(2)四边形 AOBD 是以OB 为底的直角梯形,且OA OB = 4 0, -----6 分
AD / /OB, AD ⊥ DB,-----8 分
设 D (x, y) AD = (x + 2, y 2) , BD = (x 3, y 1)
11
x =
3y 6 = x + 2 5 x = 2
或 (舍)------10 分
(x + 2)(x 3)+ ( y 2)( y 1) = 0 17 y = 2y =
5
17.(本题 13 分)
在 ABC中, BC = 4, AC = 13 , AB =1.
(I)求 B;
(II)若 D为 BC 边上一点,再从条件①、条件②、条件③这三个条件中选择一个作为已
知,使 ABD 存在且唯一确定,求 ABD 的面积.
π
条件①: ADB = ;
4
2 2
条件②: AD = ;
3
条件③: ABD 的周长为3+ 3 .
注:如果选择的条件不符合要求,第(Ⅱ)问得 0 分;如果选择多个符合要求的条件
分别解答,按第一个解答计分.
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
解:(Ⅰ)在△ABC 中,由余弦定理得
BC2 + AB2 AC2
cos B =
2BC AB
又因为 BC = 4, AC = 13 , AB =1,
42 +12 ( 13)2 1
所以cos B = = .
2 4 1 2
π
又 B (0, π) ,所以 B = . ......................................... ...........................5 分
3
π
(II)选择条件①: ADB = .
4
AD 1
AD AB =
在△ADB 中,由正弦定理 = ,得 3 2 ,
sin B sin ADB
2 2
6
所以 AD = .
2
所以 sin BAD = sin( B + ADB)
= sin Bcos ADB +cos Bsin ADB
3 2 1 2
= +
2 2 2 2
6 + 2
= .
4
1
所以 S ABD = AB ADsin BAD .
2
1 6 6 + 2
= 1
2 2 4
3+ 3
= . ......................................................................13 分
8
选择条件③:由余弦定理 AD2 = AB2 + BD2 2AB BDcos B , AB + BD + AD = 3 3 ,
2
得 (2 + 3 BD) =1+ BD2 BD ,
解得 BD = 2,
1 1 3 3
所以 S = AB BD sin B = 1 2 = . ........................ ...............13 分 ABD
2 2 2 2
18. (本题 12 分)
π π
已知函数 f (x) = 2 sin (2x + ) 的图象上所有点向右平移 个单位长度,所得函数
2 8
{#{QQABABYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
图象关于原点对称.
(1)求 的值;
1
(2)设 g (x) = f (x) 2cos2 x + ,若 g (x)在区间 (0,m)上有且只有一个零点,求m的取值
2
范围.
π π
(1)解:将函数 f (x) = 2 sin (2x + ) 的图象上所有点向右平移 个单位长度,
2 8
π π
可得到函数 y = 2 sin 2 x + = 2 sin 2x + ,-------2 分
8 4
π π
由题意可知,函数 y = 2 sin 2x + 为奇函数,则 = kπ (k Z),
4 4
π π π
可得 = + kπ (k Z),又因为 ,则 = .----------------4 分
4 2 4
π
(2)解:由(1)可知, f (x) = 2 sin 2x + = sin 2x + cos 2x,----------6 分
4
1 1 1
则 g (x) = f (x) 2cos2 x + = sin 2x + cos 2x (1+ cos 2x)+ = sin 2x ,-------8 分
2 2 2
因为0 x m,则0 2x 2m ,
1
由 g (x) = 0,可得sin 2x = ,---------10 分
2
π 5π π 5π
因为 g (x)在区间 (0,m)上有且只有一个零点,则 2m ,解得 m .
6 6 12 12
π 5π
因此,实数m的取值范围是 , .-------------------------12 分
12 12
{#{QQABBAYQShA5oggCYIQwIJJbAAACASh4CrQQ1lqKCCwgmGQkkJAAChALCUQgkgwGRwCAOAuAAIAQACAQwYBFFAABBIA=A}=#}}#}
同课章节目录
