七年级数学机会的均等与不等2
图片预览

文档简介
机会的均等与不等(二)
知识技能目标
1.了解随机事件的成功率的概念;
2.会求不确定事件的成功率.
过程性目标
让学生感受随机事件的不确定性,体会随机事件的实验成功率随实验次数的增加而逐渐趋稳.
教学过程
一、创设情境
在一次实验中,不确定事件是否会发生是无法预料的.如果发生了,我们就说它在这次实验中成功了;反之,我们就说它在这次实验中失败了.
下面我们一起来做个实验:与你的同伴合作,做一做抛掷两枚硬币的游戏,每人各抛10次,一位同学抛的时候,另一位同学帮着记录实验结果.看看不确定事件“出现两个正面”在你们俩的实验中各成功了几次.
二、探究归纳
1.下表是小华和小明的实验记录
在小华的10次实验中,成功2次,成功的频率(简称成功率)是 2/10 ,也就是20%;小明的成功率是10%.那么,10次实验中,小华和小明的失败率依次是______和_______,小华和小明成功率的差距是____.
2.下表是某班四个小组40位同学在共计400次实验中成功掷出“两个正面”的次数.
这个统计表除了告诉我们每个学生的实验结果外,还传达了哪些信息呢?
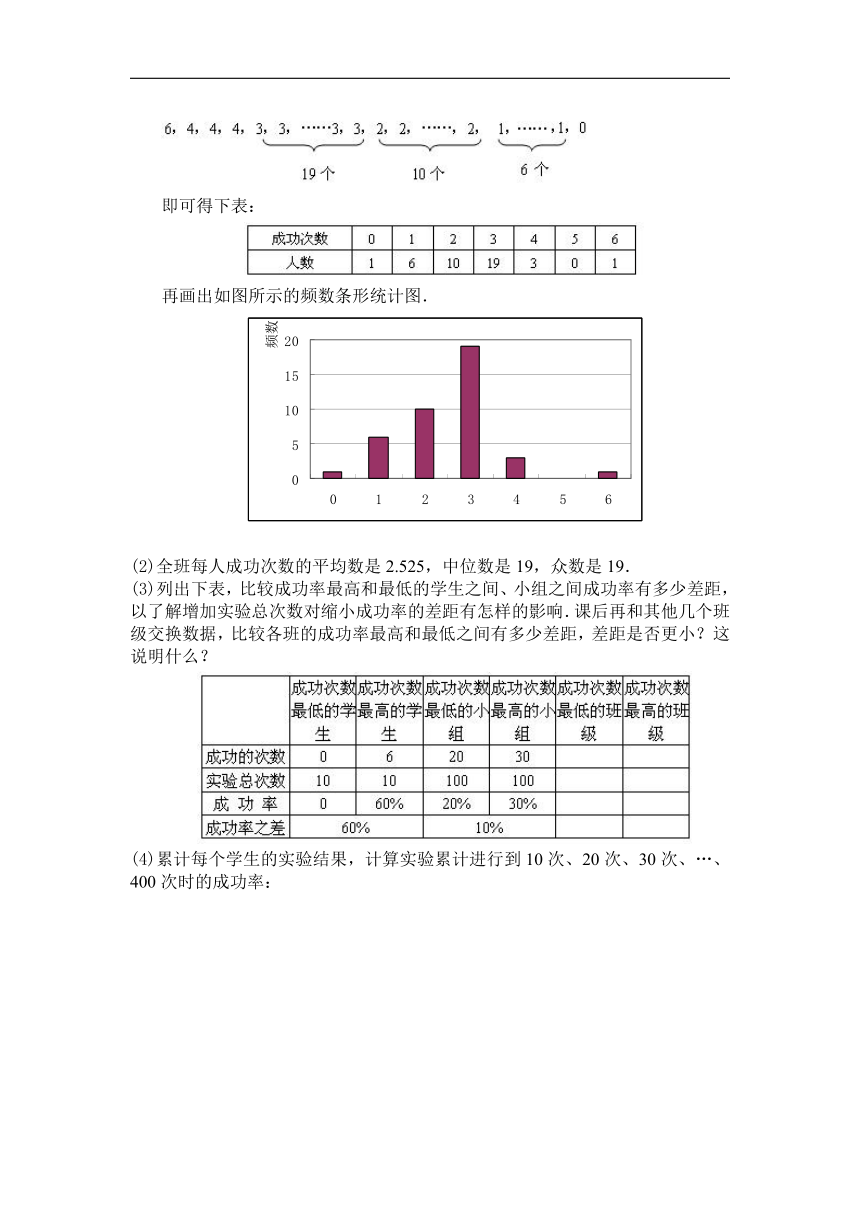
(1)先将学生的成功次数按照大小重新排列:
即可得下表:
再画出如图所示的频数条形统计图.
(2)全班每人成功次数的平均数是2.525,中位数是19,众数是19.
(3)列出下表,比较成功率最高和最低的学生之间、小组之间成功率有多少差距,以了解增加实验总次数对缩小成功率的差距有怎样的影响.课后再和其他几个班级交换数据,比较各班的成功率最高和最低之间有多少差距,差距是否更小?这说明什么?
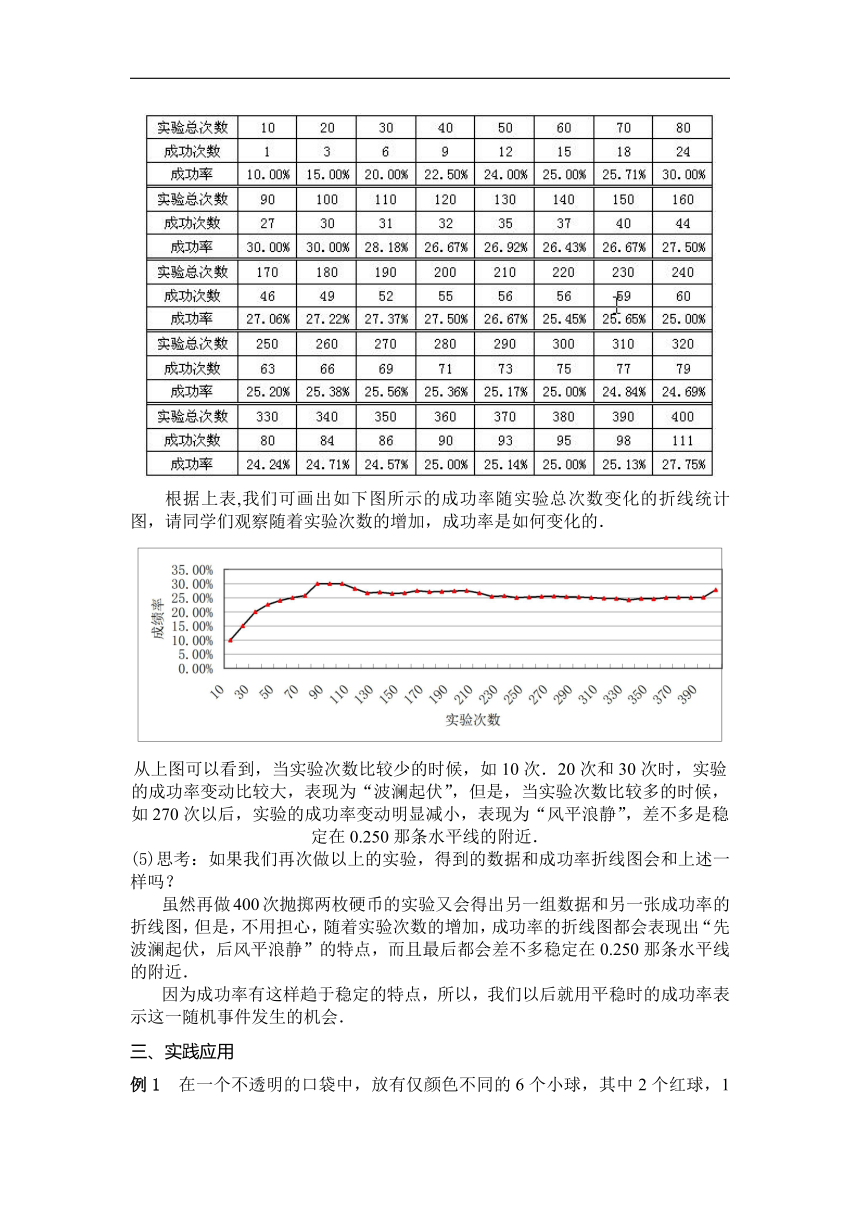
(4)累计每个学生的实验结果,计算实验累计进行到10次、20次、30次、…、400次时的成功率:
根据上表,我们可画出如下图所示的成功率随实验总次数变化的折线统计图,请同学们观察随着实验次数的增加,成功率是如何变化的.
从上图可以看到,当实验次数比较少的时候,如10次.20次和30次时,实验的成功率变动比较大,表现为“波澜起伏”,但是,当实验次数比较多的时候,如270次以后,实验的成功率变动明显减小,表现为“风平浪静”,差不多是稳定在0.250那条水平线的附近.
(5)思考:如果我们再次做以上的实验,得到的数据和成功率折线图会和上述一样吗?
虽然再做400次抛掷两枚硬币的实验又会得出另一组数据和另一张成功率的折线图,但是,不用担心,随着实验次数的增加,成功率的折线图都会表现出“先波澜起伏,后风平浪静”的特点,而且最后都会差不多稳定在0.250那条水平线的附近.
因为成功率有这样趋于稳定的特点,所以,我们以后就用平稳时的成功率表示这一随机事件发生的机会.
三、实践应用
例1 在一个不透明的口袋中,放有仅颜色不同的6个小球,其中2个红球,1个白球,3个黑球.从中任取一个,取到黑球的成功率是多少?
分析 成功率是指成功的频率,只要抓住球的总数和黑球的个数就可计算.
解 取到黑球的成功率是:3/6=50%.
例2 某同学抛掷两个硬币,分10组实验,每组20次,下面是共计200次实验中记录下的数据:
(1)在他的每次实验中,掷出_________、_________和________都是不确定事件;
(2)在他的10组实验中,掷出“两个正面”的成功次数最多的是第________组实验,掷出“两个正面”失败次数最多的是第______组实验;
(3)在他的第一组实验中,掷出“两个正面”的成功率是________,在他的前两组实验中,掷出“两个正面”的成功率是___________;
(4)累计实验结果,计算实验累计到10次,20次,30次,……,200次时抛出“两个正面”的成功率,并画出成功率随实验总次数变化的图像,观察图象,成功率大致稳定在哪个数值的附近?
分析 这题要求有一定的识表能力,同时要理解成功与失败的意义,会画图象.
解 (1)掷出“两个正面”、“一个正面”、“两个反面”等都是不确定事件;
(2)七、九;
(3)5/20 =25% , 8/40=20%;
(4)
从上可以看出,抛出“两个正面”的成功率稳定在25%左右.
四、交流反思
今天我们一起学习了随机事件的成功与失败的意义,能根据实验结果求出成功率.随着实验次数的增加,成功率的折线图会表现出“先波澜起伏,后风平浪静”的特点,即成功率会稳定在某数值附近.
五、检测反馈
1. 某位同学抛掷两枚硬币,分10组实验,每组20次,下面是共计200次实验中记录下的结果.
(1)在他的每次实验中,抛出_________、________和_______都是不确定事件;
(2)在他的10组实验中,抛出“两个正面”成功次数最多的是他第_______组实验,抛出“两个正面”失败次数最多的是他的第____组实验;
(3)在他的第1组实验中,抛出“两个正面”的成功率是__________,在他的前两组(第1组和第2组)实验中,抛出“两个正面”的成功率是_______,在他的前七组(从第1组至第7组)实验中,抛出“两个正面” 的成功率是________,在他的前八组(从第1组至第8组)实验中,抛出“两个正面” 的成功率是________.
(4)在他的10组实验中,抛出“两个正面”的成功率是__________,抛出“一个正面”的成功率是___________,抛出“没有正面”的成功率是_________,这三个成功率的和是__________.
2.随意抛掷一枚质地均匀的硬币,正面朝上的成功率有多大?当抛掷的次数较少时,似乎毫无规律.历史上曾有许多数学家对此进行研究,做了成千上万次实验,下面是四位数学家做的实验的记录:
(1)观察表格,成功率随抛掷次数的增加有什么变化?
(2)画出成功率随抛掷次数变化的折线统计图.
知识技能目标
1.了解随机事件的成功率的概念;
2.会求不确定事件的成功率.
过程性目标
让学生感受随机事件的不确定性,体会随机事件的实验成功率随实验次数的增加而逐渐趋稳.
教学过程
一、创设情境
在一次实验中,不确定事件是否会发生是无法预料的.如果发生了,我们就说它在这次实验中成功了;反之,我们就说它在这次实验中失败了.
下面我们一起来做个实验:与你的同伴合作,做一做抛掷两枚硬币的游戏,每人各抛10次,一位同学抛的时候,另一位同学帮着记录实验结果.看看不确定事件“出现两个正面”在你们俩的实验中各成功了几次.
二、探究归纳
1.下表是小华和小明的实验记录
在小华的10次实验中,成功2次,成功的频率(简称成功率)是 2/10 ,也就是20%;小明的成功率是10%.那么,10次实验中,小华和小明的失败率依次是______和_______,小华和小明成功率的差距是____.
2.下表是某班四个小组40位同学在共计400次实验中成功掷出“两个正面”的次数.
这个统计表除了告诉我们每个学生的实验结果外,还传达了哪些信息呢?
(1)先将学生的成功次数按照大小重新排列:
即可得下表:
再画出如图所示的频数条形统计图.
(2)全班每人成功次数的平均数是2.525,中位数是19,众数是19.
(3)列出下表,比较成功率最高和最低的学生之间、小组之间成功率有多少差距,以了解增加实验总次数对缩小成功率的差距有怎样的影响.课后再和其他几个班级交换数据,比较各班的成功率最高和最低之间有多少差距,差距是否更小?这说明什么?
(4)累计每个学生的实验结果,计算实验累计进行到10次、20次、30次、…、400次时的成功率:
根据上表,我们可画出如下图所示的成功率随实验总次数变化的折线统计图,请同学们观察随着实验次数的增加,成功率是如何变化的.
从上图可以看到,当实验次数比较少的时候,如10次.20次和30次时,实验的成功率变动比较大,表现为“波澜起伏”,但是,当实验次数比较多的时候,如270次以后,实验的成功率变动明显减小,表现为“风平浪静”,差不多是稳定在0.250那条水平线的附近.
(5)思考:如果我们再次做以上的实验,得到的数据和成功率折线图会和上述一样吗?
虽然再做400次抛掷两枚硬币的实验又会得出另一组数据和另一张成功率的折线图,但是,不用担心,随着实验次数的增加,成功率的折线图都会表现出“先波澜起伏,后风平浪静”的特点,而且最后都会差不多稳定在0.250那条水平线的附近.
因为成功率有这样趋于稳定的特点,所以,我们以后就用平稳时的成功率表示这一随机事件发生的机会.
三、实践应用
例1 在一个不透明的口袋中,放有仅颜色不同的6个小球,其中2个红球,1个白球,3个黑球.从中任取一个,取到黑球的成功率是多少?
分析 成功率是指成功的频率,只要抓住球的总数和黑球的个数就可计算.
解 取到黑球的成功率是:3/6=50%.
例2 某同学抛掷两个硬币,分10组实验,每组20次,下面是共计200次实验中记录下的数据:
(1)在他的每次实验中,掷出_________、_________和________都是不确定事件;
(2)在他的10组实验中,掷出“两个正面”的成功次数最多的是第________组实验,掷出“两个正面”失败次数最多的是第______组实验;
(3)在他的第一组实验中,掷出“两个正面”的成功率是________,在他的前两组实验中,掷出“两个正面”的成功率是___________;
(4)累计实验结果,计算实验累计到10次,20次,30次,……,200次时抛出“两个正面”的成功率,并画出成功率随实验总次数变化的图像,观察图象,成功率大致稳定在哪个数值的附近?
分析 这题要求有一定的识表能力,同时要理解成功与失败的意义,会画图象.
解 (1)掷出“两个正面”、“一个正面”、“两个反面”等都是不确定事件;
(2)七、九;
(3)5/20 =25% , 8/40=20%;
(4)
从上可以看出,抛出“两个正面”的成功率稳定在25%左右.
四、交流反思
今天我们一起学习了随机事件的成功与失败的意义,能根据实验结果求出成功率.随着实验次数的增加,成功率的折线图会表现出“先波澜起伏,后风平浪静”的特点,即成功率会稳定在某数值附近.
五、检测反馈
1. 某位同学抛掷两枚硬币,分10组实验,每组20次,下面是共计200次实验中记录下的结果.
(1)在他的每次实验中,抛出_________、________和_______都是不确定事件;
(2)在他的10组实验中,抛出“两个正面”成功次数最多的是他第_______组实验,抛出“两个正面”失败次数最多的是他的第____组实验;
(3)在他的第1组实验中,抛出“两个正面”的成功率是__________,在他的前两组(第1组和第2组)实验中,抛出“两个正面”的成功率是_______,在他的前七组(从第1组至第7组)实验中,抛出“两个正面” 的成功率是________,在他的前八组(从第1组至第8组)实验中,抛出“两个正面” 的成功率是________.
(4)在他的10组实验中,抛出“两个正面”的成功率是__________,抛出“一个正面”的成功率是___________,抛出“没有正面”的成功率是_________,这三个成功率的和是__________.
2.随意抛掷一枚质地均匀的硬币,正面朝上的成功率有多大?当抛掷的次数较少时,似乎毫无规律.历史上曾有许多数学家对此进行研究,做了成千上万次实验,下面是四位数学家做的实验的记录:
(1)观察表格,成功率随抛掷次数的增加有什么变化?
(2)画出成功率随抛掷次数变化的折线统计图.
