2023-2024学年湖南省长沙市浏阳高二下学期期末质量监测数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年湖南省长沙市浏阳高二下学期期末质量监测数学试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 196.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 00:00:00 | ||
图片预览





文档简介
2023-2024学年湖南省浏阳市高二下学期期末质量监测数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知向量,,且,则( )
A. B. C. D.
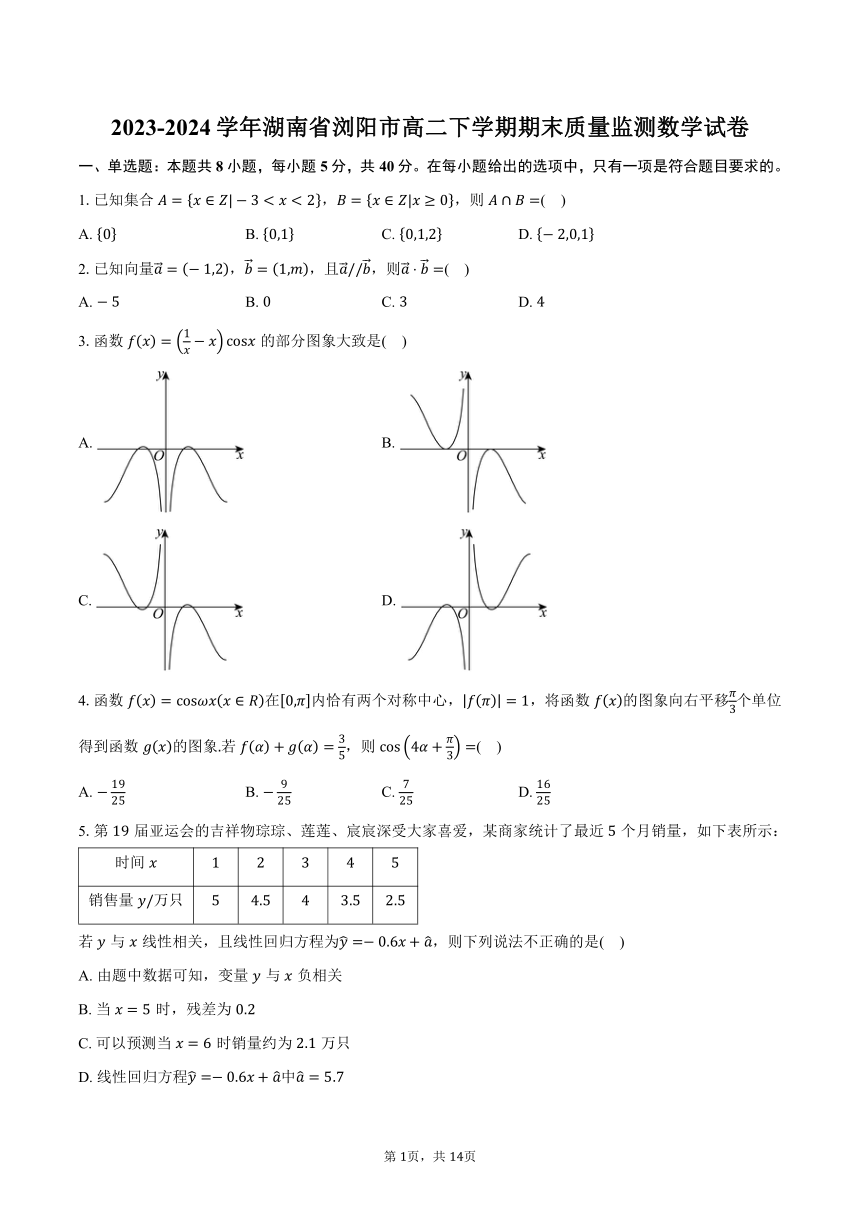
3.函数的部分图象大致是( )
A. B.
C. D.
4.函数在内恰有两个对称中心,,将函数的图象向右平移个单位得到函数的图象若,则( )
A. B. C. D.
5.第届亚运会的吉祥物琮琮、莲莲、宸宸深受大家喜爱,某商家统计了最近个月销量,如下表所示:
时间
销售量万只
若与线性相关,且线性回归方程为,则下列说法不正确的是( )
A. 由题中数据可知,变量与负相关
B. 当时,残差为
C. 可以预测当时销量约为万只
D. 线性回归方程中
6.某体育器材厂生产一批篮球,单个篮球的质量单位:克服从正态分布,从这一批篮球中随机抽检个,则被抽检的篮球的质量不小于克的个数约为( )
A. B. C. D.
7.若,且能被整除,则的最小值为( )
A. B. C. D.
8.现有名男生和名女生计划利用假期到某地景区旅游,由于是旅游的旺季,他们在景区附近订购了一家酒店的间风格不同的房间,并约定每个房间都要住人,每个房间最多住人,且男女不能混住.则不同的安排方法有种
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列命题中正确的是( )
A. 若,则
B. 若,则
C. 已知,是关于的方程的一个根,则
D. 若复数满足,则的最大值为
10.下列说法中,正确的是( )
A. 数据的第百分位数为
B. 已知随机变量服从正态分布,;则
C. 已知两个变量具有线性相关关系,其回归直线方程为;若,,,则
D. 若样本数据的方差为,则数据的方差为
11.对于任意的,表示不超过的最大整数十八世纪,被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”下列说法正确的是( )
A. 函数,的图象关于原点对称
B. 函数,的值域为
C. 对于任意的,,不等式恒成立
D. 不等式的解集为
三、填空题:本题共3小题,每小题5分,共15分。
12.函数且的图象恒过定点_______.
13.已知,则 .
14.已知在直三棱柱中,,且此三棱柱有内切球,则此三棱柱的内切球与外接球的表面积之比为_________.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知
Ⅰ若展开式的第项和第项的二项式系数相等,求的值,并求常数项
Ⅱ若展开式中所有项的系数之和为,求展开式中二项式系数最大的项.
16.本小题分
已知的内角,,的对边分别为,的面积为
.
求;
若,且的周长为,设为边中点,求.
17.本小题分
有台车床加工同一型号的零件,第台加工的次品率为,第,台加工的次品率均为,加工出来的零件混放在一起.已知第,,台车床加工的零件数分别占总数的,,.
任取一个零件,计算它是次品的概率;
如果取到的零件是次品,计算它是第台车床加工的概率.
18.本小题分
刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体每个顶点均有个面角,每个面角均为,故其各个顶点的曲率均为如图,在直三棱柱中,点的曲率为,,分别为,的中点,且.
证明:平面.
证明:平面平面.
若,求二面角的正切值.
19.本小题分
数列中,从第二项起,每一项与其前一项的差组成的数列称为的一阶差数列,记为,依此类推,的一阶差数列称为的二阶差数列,记为,如果一个数列的阶差数列是等比数列,则称数列为阶等比数列
已知数列满足,.
(ⅰ)求,,;
(ⅱ)证明:是一阶等比数列;
已知数列为二阶等比数列,其前项分别为,,,,,求及满足为整数的所有值.
答案解析
1.
【解析】解:,,
.
故选:.
2.
【解析】解:因为,所以,
所以.
3.
【解析】解:因为函数的定义域为,关于原点对称,
又,
所以函数为奇函数,排除选项;
因为,故排除;
当时,,则,且,
所以,排除.
故选D
4.
【解析】解:由得,
因为函数在内恰有两个对称中心,所以,解得,
又,所以,即,所以,
将函数的图象向右平移个单位得到函数,
即,
因为
,
所以.
故选C.
5.
【解析】
解:对于选项A,从数据看 随 的增大而减小,所以变量 与 负相关,故A正确;
对于选项B,由表中数据知 , ,
所以样本中心点为 ,将样本中心点 代入 中得 ,
所以线性回归方程为 ,所以 , ,故B错误;
对于选项C,当 时销量约为 万只,故C正确;
对于选项D,由上 ,故D正确.
6.
【解析】解:由题意得,,
,
,
所以被抽检的篮球的质量不小于克的个数约为.
故选D.
7.
【解析】解:
,
因为能被整除,
所以若能被整除,则能被整除,则的最小值为.
故选D.
8.
【解析】解:名女生需要住个房间或个房间.
若名女生住个房间,则不同的方法种数为 ,
若名女生住个房间,则不同的方法种数为 ,
则不同的安排方法有 种.
故选: .
9.
【解析】解:对于,由,则,A正确;
对于,,则,B错误;
对于,由是关于的方程的一个根,则,
所以,解得,所以,C正确;
对于,设,则,,
由可得,,故在复平面内所对应的点为以为圆心,半径为的圆,
,
表示圆上的点到点的距离,故的最大值为,故D正确.
故选:.
10.
【解析】解:对数据排列:,因为第百分位数为中位数,所以百分位数为,故 A错误;
因为随机变量服从正态分布,,所以,
所以,所以,所以,故 B正确;
因为,,,则,故 C正确;
因为样本数据的方差为,所以数据的方差为,故 D错误.
故选BC.
11.
【解析】解:对选项,当时,,
当时,,,
所以,不是奇函数,不关于原点对称,故错误;
对选项,因为,所以,
所以的值域为故正确.
对选项,,,,所以,
则,故正确.
对选项,不等式即,所以,
所以,即不等式的解集为,故D正确.
故选:.
12.
【解析】解:由对数的性质可知:,得,
当时,,
函数且的图象恒过点,
故答案为.
13.
【解析】解:令,即,因此原等式为,项为,
故答案为.
14.
【解析】解:设 ,因为 ,所以 ,
设 的内切圆的半径为 ,则 ,
即 ,解得 ,
因为三棱柱 有内切球,
所以 ,
因为 , ,
所以直三棱柱 的外接球的直径就是以 为棱的长方体的对角线,
其长为 ,
所以三棱锥 的内切球的表面积为 ,
三棱锥的外接球的表面积为 ,
所以三棱柱 的内切球与外接球的表面积之比为 .
故答案为: .
15.解:Ⅰ因为展开式的第项和第项的二项式系数相等,
所以,解得,
展开式的通项为,
令,得,
故常数项为.
Ⅱ令,得所有项的系数之和为,解得.
由于是偶数,所以展开式中共有项,且第项的二项式系数最大,
所以展开式中二项式系数最大的项为.
【解析】本题考查二项式定理的运用,考查学生的计算能力,正确运用展开式的通项是关键,属于中档题.
Ⅰ因为展开式的第项和第项的二项式系数相等,求出的值,再得出通项公式,令指数为,得到的值,即可得到常数项;
Ⅱ令,得出的值,由二项式定理的性质可得展开式中二项式系数最大的项.
16.解:依题意,,
所以,
由正弦定理可得,,
由余弦定理,,解得 ,
因为,所以 ;
依题意,,
因为,解得,
因为,
所以,
所以.
【解析】本题考查正弦定理及余弦定理,考查利用向量的数量积求向量的模,属于中档题.
由条件结合正弦定理及余弦定理即可求得,从而可求得;
由条件结合余弦定理及向量的数量积运算即可求得.
17.解:设“任取一个零件为次品”,“零件为第台车床加工”,则,,,两两互斥.根据题意得
,,,
,.
由全概率公式,得
.
“如果取到的零件是次品,计算它是第台车床加工的概率”,就是计算在发生的条件下,事件发生的概率.
.
类似地,可得
,.
【解析】本题考查条件概率,解题关键是引入字母表示事件,“任取一个零件为次品”,“零件为第台车床加工”,把所求概率事件用,表示后根据条件概率公式计算.
首先用数学语言表示已知条件,设“任取一个零件为次品”,“零件为第台车床加工”,则,,,两两互斥.,,,,.
由条件概率公式计算;
由条件概率公式计算.
18.解:在直三棱柱 中, 平面, 平面,
则 , ,所以点的曲率为 ,
所以 因为 ,所以为正三角形.
因为为的中点,所以 .
又 平面, 平面,所以 ,
因为 , 平面 ,所以 平面 .
取 的中点,连接,.
因为为的中点,所以 且 .
又 且 ,所以 且 ,
所以四边形为平行四边形,则 .
由知 平面 ,则 平面 .
又 平面 ,所以平面 平面 .
取的中点,连接,则 .
因为 平面, 平面,所以 ,
因为 , 平面 ,所以 平面 .
又 平面 ,所以 ,过作 的垂线,垂足为,连接,
则 ,又 ,、 平面 ,所以 平面 ,
又 平面 , ,
所以为二面角 的平面角的补角.
设 , ,则 , , .
由等面积法可得 ,则 ,
则 ,故二面角 的正切值为 .
【解析】本题考查了线面垂直的判定、面面垂直的判定和二面角,是中档题.
由题意可得 ,根据线面垂直的性质可得 ,结合线面垂直的判定定理即可证明;
如图,易证 ,由得 平面 ,结合面面垂直的判定定理即可证明;
如图,根据线面垂直的判定定理可得 平面 ,则 ,易证 ,则为二面角 的平面角的补角,结合等面积法求得,即可求解.
19.解:由,,
易求得,,,
由一阶差数列的定义得:
.
因为,所以,
所以当时有,
所以,
变形得,
即,,
又因为,所以,
所以为等比数列,即是一阶等比数列.
由题意知的二阶差数列为等比数列,设公比为,
则,,
所以,
由题意易求得,
所以,
所以,
即.
所以为整数当且仅当为整数,
由已知时符合题意,,,,,时不符合题意,
当时,,
所以原题等价于为整数,
因为,
显然不含质因子,所以必为的倍数,
设,,所以,
将带入式,
当为奇数时,为偶数,式为的倍数
当为偶数时,为奇数,为偶数,式为的倍数,
又因为与互质,所以式为整数.
综上,当,时,为整数.
【解析】由定义直接求值即可;
利用等比数列的定义直接证明;
由题,可知的二阶差数列为等比数列,设公比为,利用等比数列的知识求解即可.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知向量,,且,则( )
A. B. C. D.
3.函数的部分图象大致是( )
A. B.
C. D.
4.函数在内恰有两个对称中心,,将函数的图象向右平移个单位得到函数的图象若,则( )
A. B. C. D.
5.第届亚运会的吉祥物琮琮、莲莲、宸宸深受大家喜爱,某商家统计了最近个月销量,如下表所示:
时间
销售量万只
若与线性相关,且线性回归方程为,则下列说法不正确的是( )
A. 由题中数据可知,变量与负相关
B. 当时,残差为
C. 可以预测当时销量约为万只
D. 线性回归方程中
6.某体育器材厂生产一批篮球,单个篮球的质量单位:克服从正态分布,从这一批篮球中随机抽检个,则被抽检的篮球的质量不小于克的个数约为( )
A. B. C. D.
7.若,且能被整除,则的最小值为( )
A. B. C. D.
8.现有名男生和名女生计划利用假期到某地景区旅游,由于是旅游的旺季,他们在景区附近订购了一家酒店的间风格不同的房间,并约定每个房间都要住人,每个房间最多住人,且男女不能混住.则不同的安排方法有种
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列命题中正确的是( )
A. 若,则
B. 若,则
C. 已知,是关于的方程的一个根,则
D. 若复数满足,则的最大值为
10.下列说法中,正确的是( )
A. 数据的第百分位数为
B. 已知随机变量服从正态分布,;则
C. 已知两个变量具有线性相关关系,其回归直线方程为;若,,,则
D. 若样本数据的方差为,则数据的方差为
11.对于任意的,表示不超过的最大整数十八世纪,被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”下列说法正确的是( )
A. 函数,的图象关于原点对称
B. 函数,的值域为
C. 对于任意的,,不等式恒成立
D. 不等式的解集为
三、填空题:本题共3小题,每小题5分,共15分。
12.函数且的图象恒过定点_______.
13.已知,则 .
14.已知在直三棱柱中,,且此三棱柱有内切球,则此三棱柱的内切球与外接球的表面积之比为_________.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知
Ⅰ若展开式的第项和第项的二项式系数相等,求的值,并求常数项
Ⅱ若展开式中所有项的系数之和为,求展开式中二项式系数最大的项.
16.本小题分
已知的内角,,的对边分别为,的面积为
.
求;
若,且的周长为,设为边中点,求.
17.本小题分
有台车床加工同一型号的零件,第台加工的次品率为,第,台加工的次品率均为,加工出来的零件混放在一起.已知第,,台车床加工的零件数分别占总数的,,.
任取一个零件,计算它是次品的概率;
如果取到的零件是次品,计算它是第台车床加工的概率.
18.本小题分
刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体每个顶点均有个面角,每个面角均为,故其各个顶点的曲率均为如图,在直三棱柱中,点的曲率为,,分别为,的中点,且.
证明:平面.
证明:平面平面.
若,求二面角的正切值.
19.本小题分
数列中,从第二项起,每一项与其前一项的差组成的数列称为的一阶差数列,记为,依此类推,的一阶差数列称为的二阶差数列,记为,如果一个数列的阶差数列是等比数列,则称数列为阶等比数列
已知数列满足,.
(ⅰ)求,,;
(ⅱ)证明:是一阶等比数列;
已知数列为二阶等比数列,其前项分别为,,,,,求及满足为整数的所有值.
答案解析
1.
【解析】解:,,
.
故选:.
2.
【解析】解:因为,所以,
所以.
3.
【解析】解:因为函数的定义域为,关于原点对称,
又,
所以函数为奇函数,排除选项;
因为,故排除;
当时,,则,且,
所以,排除.
故选D
4.
【解析】解:由得,
因为函数在内恰有两个对称中心,所以,解得,
又,所以,即,所以,
将函数的图象向右平移个单位得到函数,
即,
因为
,
所以.
故选C.
5.
【解析】
解:对于选项A,从数据看 随 的增大而减小,所以变量 与 负相关,故A正确;
对于选项B,由表中数据知 , ,
所以样本中心点为 ,将样本中心点 代入 中得 ,
所以线性回归方程为 ,所以 , ,故B错误;
对于选项C,当 时销量约为 万只,故C正确;
对于选项D,由上 ,故D正确.
6.
【解析】解:由题意得,,
,
,
所以被抽检的篮球的质量不小于克的个数约为.
故选D.
7.
【解析】解:
,
因为能被整除,
所以若能被整除,则能被整除,则的最小值为.
故选D.
8.
【解析】解:名女生需要住个房间或个房间.
若名女生住个房间,则不同的方法种数为 ,
若名女生住个房间,则不同的方法种数为 ,
则不同的安排方法有 种.
故选: .
9.
【解析】解:对于,由,则,A正确;
对于,,则,B错误;
对于,由是关于的方程的一个根,则,
所以,解得,所以,C正确;
对于,设,则,,
由可得,,故在复平面内所对应的点为以为圆心,半径为的圆,
,
表示圆上的点到点的距离,故的最大值为,故D正确.
故选:.
10.
【解析】解:对数据排列:,因为第百分位数为中位数,所以百分位数为,故 A错误;
因为随机变量服从正态分布,,所以,
所以,所以,所以,故 B正确;
因为,,,则,故 C正确;
因为样本数据的方差为,所以数据的方差为,故 D错误.
故选BC.
11.
【解析】解:对选项,当时,,
当时,,,
所以,不是奇函数,不关于原点对称,故错误;
对选项,因为,所以,
所以的值域为故正确.
对选项,,,,所以,
则,故正确.
对选项,不等式即,所以,
所以,即不等式的解集为,故D正确.
故选:.
12.
【解析】解:由对数的性质可知:,得,
当时,,
函数且的图象恒过点,
故答案为.
13.
【解析】解:令,即,因此原等式为,项为,
故答案为.
14.
【解析】解:设 ,因为 ,所以 ,
设 的内切圆的半径为 ,则 ,
即 ,解得 ,
因为三棱柱 有内切球,
所以 ,
因为 , ,
所以直三棱柱 的外接球的直径就是以 为棱的长方体的对角线,
其长为 ,
所以三棱锥 的内切球的表面积为 ,
三棱锥的外接球的表面积为 ,
所以三棱柱 的内切球与外接球的表面积之比为 .
故答案为: .
15.解:Ⅰ因为展开式的第项和第项的二项式系数相等,
所以,解得,
展开式的通项为,
令,得,
故常数项为.
Ⅱ令,得所有项的系数之和为,解得.
由于是偶数,所以展开式中共有项,且第项的二项式系数最大,
所以展开式中二项式系数最大的项为.
【解析】本题考查二项式定理的运用,考查学生的计算能力,正确运用展开式的通项是关键,属于中档题.
Ⅰ因为展开式的第项和第项的二项式系数相等,求出的值,再得出通项公式,令指数为,得到的值,即可得到常数项;
Ⅱ令,得出的值,由二项式定理的性质可得展开式中二项式系数最大的项.
16.解:依题意,,
所以,
由正弦定理可得,,
由余弦定理,,解得 ,
因为,所以 ;
依题意,,
因为,解得,
因为,
所以,
所以.
【解析】本题考查正弦定理及余弦定理,考查利用向量的数量积求向量的模,属于中档题.
由条件结合正弦定理及余弦定理即可求得,从而可求得;
由条件结合余弦定理及向量的数量积运算即可求得.
17.解:设“任取一个零件为次品”,“零件为第台车床加工”,则,,,两两互斥.根据题意得
,,,
,.
由全概率公式,得
.
“如果取到的零件是次品,计算它是第台车床加工的概率”,就是计算在发生的条件下,事件发生的概率.
.
类似地,可得
,.
【解析】本题考查条件概率,解题关键是引入字母表示事件,“任取一个零件为次品”,“零件为第台车床加工”,把所求概率事件用,表示后根据条件概率公式计算.
首先用数学语言表示已知条件,设“任取一个零件为次品”,“零件为第台车床加工”,则,,,两两互斥.,,,,.
由条件概率公式计算;
由条件概率公式计算.
18.解:在直三棱柱 中, 平面, 平面,
则 , ,所以点的曲率为 ,
所以 因为 ,所以为正三角形.
因为为的中点,所以 .
又 平面, 平面,所以 ,
因为 , 平面 ,所以 平面 .
取 的中点,连接,.
因为为的中点,所以 且 .
又 且 ,所以 且 ,
所以四边形为平行四边形,则 .
由知 平面 ,则 平面 .
又 平面 ,所以平面 平面 .
取的中点,连接,则 .
因为 平面, 平面,所以 ,
因为 , 平面 ,所以 平面 .
又 平面 ,所以 ,过作 的垂线,垂足为,连接,
则 ,又 ,、 平面 ,所以 平面 ,
又 平面 , ,
所以为二面角 的平面角的补角.
设 , ,则 , , .
由等面积法可得 ,则 ,
则 ,故二面角 的正切值为 .
【解析】本题考查了线面垂直的判定、面面垂直的判定和二面角,是中档题.
由题意可得 ,根据线面垂直的性质可得 ,结合线面垂直的判定定理即可证明;
如图,易证 ,由得 平面 ,结合面面垂直的判定定理即可证明;
如图,根据线面垂直的判定定理可得 平面 ,则 ,易证 ,则为二面角 的平面角的补角,结合等面积法求得,即可求解.
19.解:由,,
易求得,,,
由一阶差数列的定义得:
.
因为,所以,
所以当时有,
所以,
变形得,
即,,
又因为,所以,
所以为等比数列,即是一阶等比数列.
由题意知的二阶差数列为等比数列,设公比为,
则,,
所以,
由题意易求得,
所以,
所以,
即.
所以为整数当且仅当为整数,
由已知时符合题意,,,,,时不符合题意,
当时,,
所以原题等价于为整数,
因为,
显然不含质因子,所以必为的倍数,
设,,所以,
将带入式,
当为奇数时,为偶数,式为的倍数
当为偶数时,为奇数,为偶数,式为的倍数,
又因为与互质,所以式为整数.
综上,当,时,为整数.
【解析】由定义直接求值即可;
利用等比数列的定义直接证明;
由题,可知的二阶差数列为等比数列,设公比为,利用等比数列的知识求解即可.
第1页,共1页
同课章节目录
