【举一反三题型总结】苏教版五上 第二单元 梯形的面积(知识点+例题+变式题)
文档属性
| 名称 | 【举一反三题型总结】苏教版五上 第二单元 梯形的面积(知识点+例题+变式题) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 19:15:29 | ||
图片预览




文档简介
梯形的面积知识点梳理+题型总结
知识点:梯形的面积公式:
梯形面积=(上底+下底)×高÷2
梯形上底=面积×2÷高-下底
梯形下底=面积×2÷高-上底
梯形高=面积×2÷底
知识点:梯形的面积公式基础应用
【例题】 两个完全相同的梯形可以拼成一个( )。这个平行四边形的底等于( ),平行四边形的高等于( )。每个梯形的面积等于拼成的平行四边形的面积的( ),因为平行四边形的面积等于( ),所以梯形的面积等于( )。
答案:平行四边形,梯形的上底+下底,梯形的高,一半,底×高,(上底+下底)×高÷2
【变式题】 一个长方形被分割成两个完全一样的梯形。如果长方形的长是10cm,宽是5cm,那么其中一个梯形的面积是( )。
答案:25平方厘米
【变式题】 一个梯形的面积是42平方米,它的上、下底之和与一个平行四边形的底边相等,高与平行四边形的高相等,这个平行四边形的面积是( )平方米。
答案:84平方米
重难点一:梯形的面积的逆公式
【例题】 一个梯形的上底是8cm,下底是10cm,面积是45cm 。这个梯形的高是多少厘米
答案:梯形高=面积×2÷底 ,45×2÷(8+10)=5厘米
【变式题】 一个梯形的面积是150平方厘米,它的上底是37厘米,下底是13厘米,则它的高是( )厘米。
答案:梯形高=面积×2÷底 ,150×2÷(37+13)=6厘米
【变式题】 一个梯形上底是16分米,高是20分米,两个这样的梯形面积是12平方米,这个梯形的下底长多少分米
答案:梯形下底=面积×2÷高-上底 ,12平方米=12平方分米,1200×2÷20-16=104分米
重难点二:梯形底和高的变化与面积变化的变化
【例题】 一个梯形的高不变,上底扩大为原来的2倍,下底也扩大为原来的2倍,它的面积就扩大为原来的( )倍。
答案:2倍
【变式题】一个梯形原来的面积是180平方厘米,如果它的上底、下底均不变,高扩大到原来的4倍,那么现在的面积是( )平方厘米;如果它的上底和下底均扩大到原来的3倍,高扩大到原来的2倍,那么现在的面积是( )平方厘米。
答案:720平方厘米,1080平方厘米
重难点三:篱笆问题
【例题】 如下图,李大爷用篱笆靠墙围成了一个直角梯形的养鸡场,篱笆长86米,养鸡场的面积是多少平方米
答案:根据题意可知,上底与下底的和是86-26=60厘米,利用梯形的面积公式,60×26÷2=780平方米
【变式题】 张爷爷靠墙用篱笆围了一个直角梯形的鸡舍,篱笆长50米,鸡舍的面积是多少平方米
答案:上底与下底的和50-10=40米,40×10÷2=200平方米
拓展点一:运用分析法解决梯形中求面积最大的问题
【例题】在一个上底是11分米,下底是18分米,高是22分米的梯形中,剪下一个最大的三角形,剩下的面积是多少
答案:方法一(11+18)×22÷2=319(平方分米)18×222=198(平方分米)319-198=121(平方分米)
方法二11×22÷2=121(平方分米)
答:剩下的面积是121平方分米。
解析:此类习题可借助画图并根据数量关系“梯形的面积一最大三角形的面积=剩下的面积”解决;也可直接根据“底×高÷2”求出三角形的面积。
【变式题】在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少
答案:方法一:(5+7)×4÷2-5×4=4(cm2)方法二:(7-5)×4÷2=4(cm2)[提示:
在梯形中剪去一个最大的平行四边形,这个平行四边形应该是以梯形的上底为底,梯形的高为高的平行四边形,剩下的图形是一个三角形。
【变式题】已知一个直角梯形上底是84厘米,下底是156厘米,在这个直角梯形中剪去一个最大的三角形(如图),剩下的面积是3780平方厘米。原来梯形的面积是多少
答案:3780×2÷84=90(厘米)
(84+156)×90÷2=10800(平方厘米)
拓展点二:添加辅助线解题
【例题】 如图,一个平行四边形被分割成一个梯形和一个三角形。如果梯形的面积比三角形的面积大12平方米,那么梯形的面积是( )平方米,三角形的面积是( )平方米。
答案:梯形与三角形的面积的和是16x6=96(平方米),梯形与三角形的面积的差是19平方米则梯形的面积是(96+12)÷2=54(平方米故答案为:54.
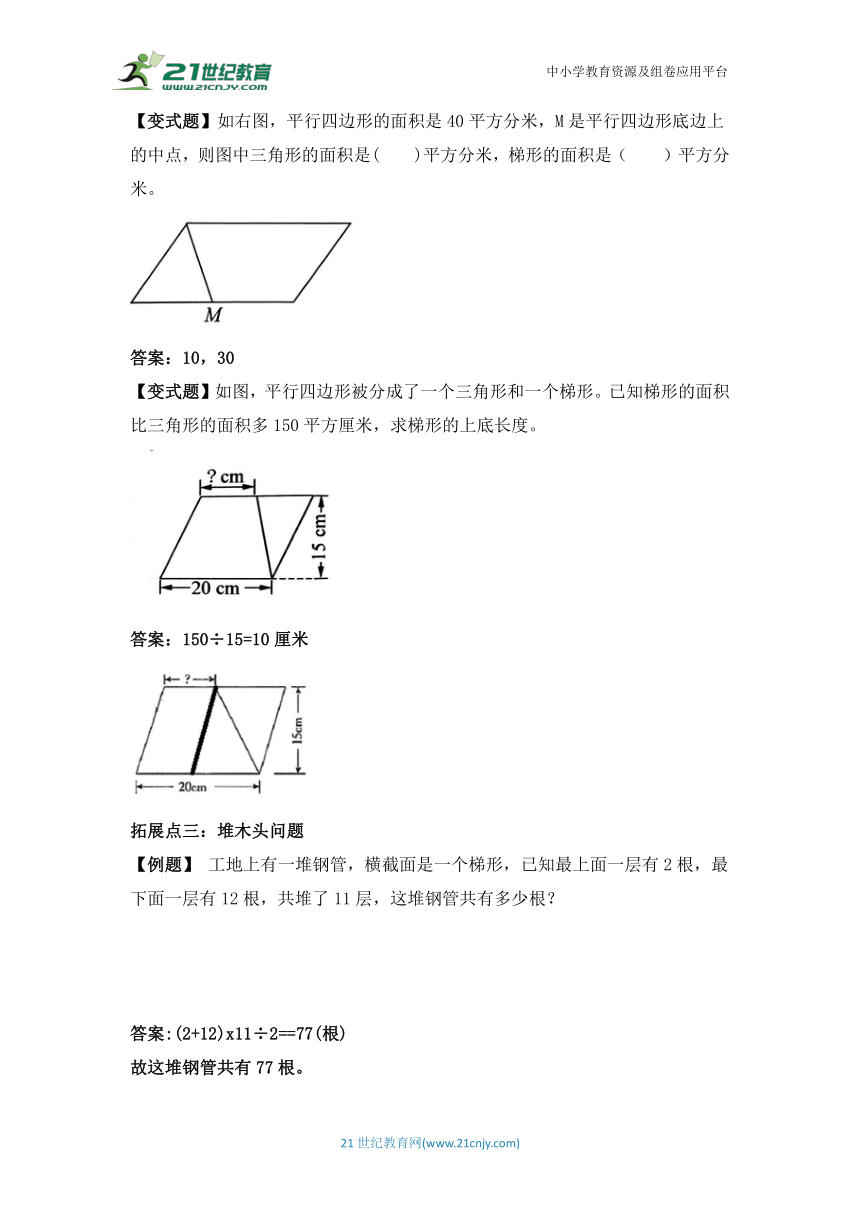
【变式题】如右图,平行四边形的面积是40平方分米,M是平行四边形底边上的中点,则图中三角形的面积是( )平方分米,梯形的面积是( )平方分米。
答案:10,30
【变式题】如图,平行四边形被分成了一个三角形和一个梯形。已知梯形的面积比三角形的面积多150平方厘米,求梯形的上底长度。
答案:150÷15=10厘米
拓展点三:堆木头问题
【例题】 工地上有一堆钢管,横截面是一个梯形,已知最上面一层有2根,最下面一层有12根,共堆了11层,这堆钢管共有多少根?
答案:(2+12)x11÷2==77(根)
故这堆钢管共有77根。
解析:本题是一道关于梯形面积公式灵活应用的问题关键是确定平面图形是梯形;【解题方法提示】分析题意,用上层的根数加上下层的根数的和乘以层数除以2.即可求出钢管的根数;联系已知数据,根据上述公式进行计算,即可求出这堆钢管的根数。
【变式题】 一堆木头整齐地叠放在地上,最下面一层有 25 根,最上面一层有6根,每下面一层都要比它上面一层多一根。这堆木头一共有几根?
答案:(6+25)×20÷2=310根
【变式题】 一堆钢管,最上面一层有10根,最底层有30根,而且下一层总比上一层多1根。这堆钢管一共有多少根?
答案:(10+30)×21÷2=420根
一、选择题
1.王叔叔准备用长120米的栅栏,在农场的墙壁旁圈一块梯形形状的地用于种菜(如图所示),这块地的面积是( )平方米。
A.3200 B.1600
C.2400 D.4800
2.一堆圆木,堆成梯形的形状,下层18根,上层7根,每相邻两层差一根,这堆圆木共有( )根。
A.57 B.50 C.150 D.180
3.如下图,梯形甲的面积( )梯形乙的面积。
A.大于 B.等于 C.小于 D.无法确定
二、填空题
4.小刚同学通过如上图所示的操作,把梯形转化成平行四边形。已知原来梯形的高是8厘米,A、B两点是梯形两条腰的中点。线段AB长6厘米。那么转化后平行四边形的底是( )厘米,原来梯形的面积是( )平方厘米。
5.如图,梯形的面积是54平方厘米,那么梯形的高是( )厘米,阴影部分的面积是( )平方厘米,在该图形中画一个最大的平行四边形,那么这个平行四边形的面积是( )平方厘米。
6.如图,把一个平行四边形剪成一个三角形和一个梯形,如果平行四边形的高是0.6分米,那么三角形的面积是( )平方分米,梯形的面积是( )平方分米。
7.一个梯形的面积是60平方厘米,如果高不变,把它的上底延长5厘米,下底缩短5厘米后,梯形的面积是( )平方厘米。
8.有一堆钢管,最上层有5根,最下层有15根,每相邻两层相差1根,共有11层,这堆钢管共有( )根。
9.一堆钢管,最下面一层有24根,每增加一层根数就减少1根,一共堆了8层,这堆钢管一共有( )根。
10.一块面积为45平方米的三角形菜地,它的高是15米,它的底是( )米;一个梯形的面积是18平方厘米,上底与下底的和是9厘米,高是( )厘米。
11.如图所示,长方形与平行四边形部分重叠,已知梯形甲的面积是35cm2。则梯形乙的面积是( )cm2。
三、计算题
12.计算下面图形的面积。
13.求下面图形的面积。(单位:cm)
四、作图题
14.如图每个小方格边长1厘米,请在方格中画出面积是12平方厘米的平行四边形,再画出与它面积相等的三角形和梯形各一个。
五、解答题
15.用两个完全一样的梯形拼成一个平行四边形(如下图),每个梯形的面积是多少平方厘米?
16.如图,长方形被分成了一个三角形和一个梯形。已知三角形的面积比梯形少180平方厘米,求三角形和梯形的面积。
17.一个梯形的下底长是18厘米,如果把上底延长12厘米,就成了一个平行四边形,面积增加了24平方厘米。那么原来梯形的面积是多少平方厘米?
18.一个梯形的上底是10厘米,如果把上底延长5厘米就变成了一个面积120平方厘米的平行四边形,原来梯形的面积是多少平方厘米?
19.绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如图),草坪的面积是多少平方米?
20.一个牧场的形状如图。
这个牧场的面积是多少平方米?是多少公顷?
21.实验小学的报告厅一共有20排座位。其中第一排有10个座位,第二排有12个座位,后面每一排的座位数都比前一排多2个。实验小学的报告厅一共有多少个座位?
22.王老师请广告公司制作一块梯形广告牌,这块广告牌的上底是3.6米,下底是8.4米,高是4米。如果这个广告公司制作广告牌每平方米收费25元,那么王老师要付给这个广告公司多少元?
23.如下图,梯形的面积是64平方厘米,阴影部分的面积是多少?
24.如图,两个完全相同的直角梯形重叠在一起,求阴影部分的面积。(单位:厘米)
25.如图所示,两个完全一样的直角三角形重叠在一起,求阴影部分的面积。(单位:cm)
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】结合题意观察图可知:这块地的面积也就是梯形的面积,梯形的面积=(上底+下底)×高÷2,用栅栏总长度120米减去梯形的高40米,即可求出梯形的上底+下底的长度。据此解答。
【详解】(120-40)×40÷2
=80×40÷2
=3200÷2
=1600(平方米)
所以,这块地的面积是1600平方米。
故答案为:B
2.C
【分析】借鉴梯形面积公式,圆木总根数=(上层根数+下层根数)×层数÷2,总层数=下层根数-上层根数+1,据此列式计算。
【详解】18-7+1=12(层)
(7+18)×12÷2
=25×12÷2
=150(根)
这堆圆木共有150根。
故答案为:C
3.B
【分析】观察图形可知,甲图是长方形面积减去空白三角形面积,乙图面积是平行四边形面积减去空白三角形面积;根据长方形面积公式:面积=长×宽;平行四边形面积公式:面积=底×高;长方形的宽=平行四边形的底;长方形的长=平行四边形的高,由此可知,长方形面积=平行四边形面积;由于空白三角形是公共部分的面积,所以甲的面积等于乙的面积,据此解答。
【详解】根据分析可知,如下图,梯形甲的面积等于乙图面积。
故答案为:B
【点睛】明确平行四边形面积与长方形面积的关系是解答本题的关键。
4. 12 48
【分析】根据题意,把梯形转化成平行四边形,那么梯形的面积等于平行四边形的面积。
观察图形可知,平行四边形的底等于AB的2倍,平行四边形的高等于梯形高的一半,根据平行四边形的面积=底×高,求出平行四边形的面积,也是原来梯形的面积。
【详解】平行四边形的底:6×2=12(厘米)
平行四边形的高:8÷2=4(厘米)
面积:12×4=48(平方厘米)
那么转化后平行四边形的底是12厘米,原来梯形的面积是48平方厘米。
5. 7.2 21.6 43.2
【分析】根据公式:梯形的高=面积×2÷(上底+下底),即可求出梯形的高;阴影部分是个三角形,根据公式:三角形的面积=底×高÷2,即可求出阴影部分的面积;这个梯形内最大的平行四边形的底与梯形的上底相等,高与梯形的高相等,根据公式:平行四边形的面积=底×高,即可求出平行四边形的面积。
【详解】54×2÷(6+9)
=54×2÷15
=108÷15
=7.2(厘米);
6×7.2÷2
=43.2÷2
=21.6(平方厘米);
6×7.2=43.2(平方厘米)。
即梯形的高是7.2厘米,阴影部分的面积是21.6平方厘米,平行四边形的面积是43.2平方厘米。
6. 0.126 0.294
【分析】看图,三角形和梯形的高,与平行四边形的高相等。三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,据此列式求出这个三角形和梯形的面积。
【详解】0.42×0.6÷2
=0.252÷2
=0.126(平方分米)
(0.7+0.7-0.42)×0.6÷2
=0.98×0.6÷2
=0.294(平方分米)
所以,三角形的面积是0.126平方分米,梯形的面积是0.294平方分米。
7.60
【分析】根据题意,梯形的高不变,把它的上底延长5厘米,下底缩短5厘米,则梯形的上、下底之和不变,根据梯形的面积=(上底+下底)×高÷2可知,梯形的面积不变。
【详解】梯形的上底延长5厘米,下底缩短5厘米后,那么:
梯形的面积=(上底+5+下底-5)×高÷2=(上底+下底)×高÷2
即梯形的上、下底之和不变,高不变,则梯形的面积不变,所以梯形的面积是60平方厘米。
8.110
【分析】
最上层有5根,最下层有15根,每相邻两层相差1根,共有11层,则可以看成一个梯形,按照梯形的面积的面积求出钢管的个数。梯形的面积=(上底+下底)×高÷2,上底是5,下底是15,一共有11层,则高是11。
【详解】(5+15)×11÷2
=20×11÷2
=110(根)
则这堆钢管共有110根。
9.164
【分析】因为每增加一层根数就减少1根,所以最上层的根数等于最下层的根减去层数加1,据此前项最上层的根数,然后根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】(24-8+1+24)×8÷2
=(16+1+24)×8÷2
=(17+24)×8÷2
=41×8÷2
=328÷2
=164(根)
这堆钢管一共有164根。
10. 6 4
【分析】(1)三角形的面积=底×高÷2,则三角形的底=三角形的面积×2÷高。
(2)梯形的面积=(上底+下底)×高÷2,则梯形的高=梯形的面积×2÷(上底+下底)。
【详解】45×2÷15
=90÷15
=6(米)
则三角形的底是6米。
18×2÷9
=36÷9
=4(厘米)
则梯形的高是4厘米。
11.35
【分析】根据图示可知,长方形与平行四边形等底等高,所以长方形的面积等于平行四边形的面积。S甲=S长方形-S空白,S乙=S平行四边形-S空白,所以梯形乙的面积和梯形甲的面积相等,是35cm2。
【详解】根据分析,梯形乙的面积和梯形甲的面积相等,是35cm2。
12.84cm2;54m2;192cm2
【分析】(1)根据平行四边形的面积=底×高,代入数据计算即可求解。
(2)观察图形可知,组合图形的面积=三角形的面积+梯形的面积,根据三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算即可求解。
(3)如下图,补齐缺口处,那么组合图形的面积=梯形的面积-正方形的面积,根据梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,代入数据计算即可求解。
【详解】(1)8×10.5=84(cm2)
平行四边形的面积是84cm2。
(2)9×4÷2+(9+3)×6÷2
=36÷2+12×6÷2
=18+36
=54(m2)
组合图形的面积是54m2。
(3)(8+24)×(8+8)÷2-8×8
=32×16÷2-64
=256-64
=192(cm2)
组合图形的面积是192cm2。
13.700cm2;282cm2;64cm2
【分析】(1)组合图形的面积=梯形的面积+正方形的面积,根据梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,代入数据计算求解。
(2)组合图形的面积=平行四边形的面积+三角形的面积,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,代入数据计算求解。
(3)组合图形的面积=长方形的面积-梯形的面积,根据长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,代入数据计算求解。
【详解】(1)(20+40)×10÷2+20×20
=60×10÷2+400
=300+400
=700(cm2)
组合图形的面积是700cm2。
(2)12×16+20×9÷2
=192+90
=282(cm2)
组合图形的面积是282cm2。
(3)10×8-(6+10)×2÷2
=80-16×2÷2
=80-16
=64(cm2)
组合图形的面积是64cm2。
14.见详解
【分析】每个图形的面积是12平方厘米,将12拆分成6×2,根据平行四边形的面积公式,用6厘米当作平行四边形的底,2厘米当平行四边形的高;根据三角形的面积=底×高÷2,将12×2拆分成3×8,用8厘米当三角形的底,3厘米当三角形的高;根据梯形的面积=(上底+下底)×高÷2,将12×2拆分成6×4,再将6拆分成2+4,然后用2厘米当梯形的上底,4厘米当梯形的下底,4厘米当梯形的高,据此画图。
【详解】如图:
(答案不唯一)
15.320平方厘米
【分析】根据题意,用两个完全一样的梯形拼成一个底为40厘米、高为16厘米的平行四边形,根据平行四边形的面积=底×高,求出平行四边形的面积,也就是两个梯形的面积,再除以2,即是每个梯形的面积。
【详解】40×16÷2
=640÷2
=320(平方厘米)
答:每个梯形的面积是320平方厘米。
16.210平方厘米;390平方厘米
【分析】通过做辅助线可知,梯形比三角形多的就是小长方形的面积,根据长方形面积=长×宽,可以求出小长方形的宽,也就是梯形的上底。三角形的底=30厘米-小长方形的宽,三角形的高是20厘米。
根据公式:三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】
如图所示:
180÷20=9(厘米)
30-9=21(厘米)
21×20÷2
=420÷2
=210(平方厘米)
(9+30)×20÷2
=39×20÷2
=780÷2
=390(平方厘米)
答:三角形的面积是210平方厘米,梯形的面积是390平方厘米。
17.48平方厘米
【分析】由题意可知:增加部分是一个三角形,其面积和底已知,于是即可求出三角形的高,也就等于知道了梯形的高,进而依据梯形的面积公式即可求解。
【详解】24×2÷12
=48÷12
=4(厘米)
(18-12+18)×4÷2
=24×4÷2
=48(平方厘米)
答:梯形的面积是48平方厘米。
18.100平方厘米
【分析】读题可知,平行四边形的底=梯形下底,平行四边形的高=梯形的高,梯形上底+5厘米=下底,根据平行四边形的高=面积÷底,梯形面积=(上底+下底)×高÷2,列式解答即可。
【详解】10+5=15(厘米)
120÷15=8(厘米)
(10+15)×8÷2
=25×8÷2
=100(平方厘米)
答:原来梯形的面积是100平方厘米。
19.512平方米
【分析】由图可知,草坪的面积=梯形草坪的面积-长方形的花坛,根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据解答即可。
【详解】(20+36)×20÷2
=56×20÷2
=1120÷2
=560(平方米)
12×4=48(平方米)
560-48=512(平方米)
答:草坪的面积是512平方米。
20.40000平方米;4公顷
【分析】牧场的面积=两个梯形的面积,根据梯形的面积=(上底+下底)×高÷2,代入数据,即可求出牧场的面积,再根据1公顷=10000平方米,低级单位化高级单位除以进率即可解答。
【详解】(30+220)×(230-150)÷2
=250×80÷2
=20000÷2
=10000(平方米)
(180+220)×150÷2
=400×150÷2
=60000÷2
=30000(平方米)
10000+30000=40000(平方米)
40000平方米=4公顷
答:这个牧场的面积是40000平方米,是4公顷。
21.580个
【分析】
后面每一排的座位数都比前一排多2个,共有20排座位,因此最后一排座位数=第一排座位数+2×(总排数-1),座位的摆放类似一个梯形,根据梯形面积公式,座位总数=(第一排座位数+最后一排座位数)×排数÷2,据此列式解答。
【详解】最后一排座位数:10+2×(20-1)
=10+2×19
=10+38
=48(个)
座位总数:(10+48)×20÷2
=58×20÷2
=580(个)
答:实验小学的报告厅一共有580个座位。
22.600元
【分析】根据梯形面积=(上底+下底)×高÷2,求出广告牌面积,广告牌面积×每平方米收费=要付的钱数,据此列式解答。
【详解】(3.6+8.4)×4÷2×25
=12×4÷2×25
=24×25
=600(元)
答:王老师要付给这个广告公司600元。
23.52平方厘米
【分析】阴影部分是底是13厘米,高等于梯形高的三角形;根据梯形的面积公式:面积=(上底+下底)×高÷2,高=面积×2÷(上底+下底),代入数据,求出梯形的高,也就是阴影部分三角形的高;再根据三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】64×2÷(3+13)
=128÷16
=8(厘米)
13×8÷2
=104÷2
=52(平方厘米)
答:阴影部分面积是52平方厘米。
24.33平方厘米
【分析】如图所示,因为空白a是两个直角梯形的公共部分,去掉公共部分,则剩下的部分底面积也相等,即空白b和阴影部分的面积相等,而空白b的下底已知,高就是3厘米,上底可以求出,于是利用梯形的面积公式即(上底+下底)×高÷2可求解。
【详解】(12-2+12)×3÷2
=22×3÷2
=66÷2
=33(平方厘米)
答:阴影部分的面积是33平方厘米。
【点睛】解答此题的关键是明白阴影部分的面积就等于空白b的面积,从而可以利用梯形面积公式求解。
25.18cm2
【分析】阴影部分面积=大三角形的面积先减去一个小三角形面积,左边梯形面积也是由大三角形面积减去小三角形面积,所以梯形面积与阴影部分面积相等,根据梯形面积公式:(上底+下底)×高÷2,上底是(6-3)cm,下底是6cm,高是4cm,代入数据,即可解答。
【详解】(6-3+6)×4÷2
=(3+6)×4÷2
=9×4÷2
=36÷2
=18(cm2)
答:阴影部分面积是18cm2。
【点睛】本题考查组合图形面积的计算,根据图形的特征,通过转化的方法,将阴影部分面积转化为梯形,从而求出面积。
知识点:梯形的面积公式:
梯形面积=(上底+下底)×高÷2
梯形上底=面积×2÷高-下底
梯形下底=面积×2÷高-上底
梯形高=面积×2÷底
知识点:梯形的面积公式基础应用
【例题】 两个完全相同的梯形可以拼成一个( )。这个平行四边形的底等于( ),平行四边形的高等于( )。每个梯形的面积等于拼成的平行四边形的面积的( ),因为平行四边形的面积等于( ),所以梯形的面积等于( )。
答案:平行四边形,梯形的上底+下底,梯形的高,一半,底×高,(上底+下底)×高÷2
【变式题】 一个长方形被分割成两个完全一样的梯形。如果长方形的长是10cm,宽是5cm,那么其中一个梯形的面积是( )。
答案:25平方厘米
【变式题】 一个梯形的面积是42平方米,它的上、下底之和与一个平行四边形的底边相等,高与平行四边形的高相等,这个平行四边形的面积是( )平方米。
答案:84平方米
重难点一:梯形的面积的逆公式
【例题】 一个梯形的上底是8cm,下底是10cm,面积是45cm 。这个梯形的高是多少厘米
答案:梯形高=面积×2÷底 ,45×2÷(8+10)=5厘米
【变式题】 一个梯形的面积是150平方厘米,它的上底是37厘米,下底是13厘米,则它的高是( )厘米。
答案:梯形高=面积×2÷底 ,150×2÷(37+13)=6厘米
【变式题】 一个梯形上底是16分米,高是20分米,两个这样的梯形面积是12平方米,这个梯形的下底长多少分米
答案:梯形下底=面积×2÷高-上底 ,12平方米=12平方分米,1200×2÷20-16=104分米
重难点二:梯形底和高的变化与面积变化的变化
【例题】 一个梯形的高不变,上底扩大为原来的2倍,下底也扩大为原来的2倍,它的面积就扩大为原来的( )倍。
答案:2倍
【变式题】一个梯形原来的面积是180平方厘米,如果它的上底、下底均不变,高扩大到原来的4倍,那么现在的面积是( )平方厘米;如果它的上底和下底均扩大到原来的3倍,高扩大到原来的2倍,那么现在的面积是( )平方厘米。
答案:720平方厘米,1080平方厘米
重难点三:篱笆问题
【例题】 如下图,李大爷用篱笆靠墙围成了一个直角梯形的养鸡场,篱笆长86米,养鸡场的面积是多少平方米
答案:根据题意可知,上底与下底的和是86-26=60厘米,利用梯形的面积公式,60×26÷2=780平方米
【变式题】 张爷爷靠墙用篱笆围了一个直角梯形的鸡舍,篱笆长50米,鸡舍的面积是多少平方米
答案:上底与下底的和50-10=40米,40×10÷2=200平方米
拓展点一:运用分析法解决梯形中求面积最大的问题
【例题】在一个上底是11分米,下底是18分米,高是22分米的梯形中,剪下一个最大的三角形,剩下的面积是多少
答案:方法一(11+18)×22÷2=319(平方分米)18×222=198(平方分米)319-198=121(平方分米)
方法二11×22÷2=121(平方分米)
答:剩下的面积是121平方分米。
解析:此类习题可借助画图并根据数量关系“梯形的面积一最大三角形的面积=剩下的面积”解决;也可直接根据“底×高÷2”求出三角形的面积。
【变式题】在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少
答案:方法一:(5+7)×4÷2-5×4=4(cm2)方法二:(7-5)×4÷2=4(cm2)[提示:
在梯形中剪去一个最大的平行四边形,这个平行四边形应该是以梯形的上底为底,梯形的高为高的平行四边形,剩下的图形是一个三角形。
【变式题】已知一个直角梯形上底是84厘米,下底是156厘米,在这个直角梯形中剪去一个最大的三角形(如图),剩下的面积是3780平方厘米。原来梯形的面积是多少
答案:3780×2÷84=90(厘米)
(84+156)×90÷2=10800(平方厘米)
拓展点二:添加辅助线解题
【例题】 如图,一个平行四边形被分割成一个梯形和一个三角形。如果梯形的面积比三角形的面积大12平方米,那么梯形的面积是( )平方米,三角形的面积是( )平方米。
答案:梯形与三角形的面积的和是16x6=96(平方米),梯形与三角形的面积的差是19平方米则梯形的面积是(96+12)÷2=54(平方米故答案为:54.
【变式题】如右图,平行四边形的面积是40平方分米,M是平行四边形底边上的中点,则图中三角形的面积是( )平方分米,梯形的面积是( )平方分米。
答案:10,30
【变式题】如图,平行四边形被分成了一个三角形和一个梯形。已知梯形的面积比三角形的面积多150平方厘米,求梯形的上底长度。
答案:150÷15=10厘米
拓展点三:堆木头问题
【例题】 工地上有一堆钢管,横截面是一个梯形,已知最上面一层有2根,最下面一层有12根,共堆了11层,这堆钢管共有多少根?
答案:(2+12)x11÷2==77(根)
故这堆钢管共有77根。
解析:本题是一道关于梯形面积公式灵活应用的问题关键是确定平面图形是梯形;【解题方法提示】分析题意,用上层的根数加上下层的根数的和乘以层数除以2.即可求出钢管的根数;联系已知数据,根据上述公式进行计算,即可求出这堆钢管的根数。
【变式题】 一堆木头整齐地叠放在地上,最下面一层有 25 根,最上面一层有6根,每下面一层都要比它上面一层多一根。这堆木头一共有几根?
答案:(6+25)×20÷2=310根
【变式题】 一堆钢管,最上面一层有10根,最底层有30根,而且下一层总比上一层多1根。这堆钢管一共有多少根?
答案:(10+30)×21÷2=420根
一、选择题
1.王叔叔准备用长120米的栅栏,在农场的墙壁旁圈一块梯形形状的地用于种菜(如图所示),这块地的面积是( )平方米。
A.3200 B.1600
C.2400 D.4800
2.一堆圆木,堆成梯形的形状,下层18根,上层7根,每相邻两层差一根,这堆圆木共有( )根。
A.57 B.50 C.150 D.180
3.如下图,梯形甲的面积( )梯形乙的面积。
A.大于 B.等于 C.小于 D.无法确定
二、填空题
4.小刚同学通过如上图所示的操作,把梯形转化成平行四边形。已知原来梯形的高是8厘米,A、B两点是梯形两条腰的中点。线段AB长6厘米。那么转化后平行四边形的底是( )厘米,原来梯形的面积是( )平方厘米。
5.如图,梯形的面积是54平方厘米,那么梯形的高是( )厘米,阴影部分的面积是( )平方厘米,在该图形中画一个最大的平行四边形,那么这个平行四边形的面积是( )平方厘米。
6.如图,把一个平行四边形剪成一个三角形和一个梯形,如果平行四边形的高是0.6分米,那么三角形的面积是( )平方分米,梯形的面积是( )平方分米。
7.一个梯形的面积是60平方厘米,如果高不变,把它的上底延长5厘米,下底缩短5厘米后,梯形的面积是( )平方厘米。
8.有一堆钢管,最上层有5根,最下层有15根,每相邻两层相差1根,共有11层,这堆钢管共有( )根。
9.一堆钢管,最下面一层有24根,每增加一层根数就减少1根,一共堆了8层,这堆钢管一共有( )根。
10.一块面积为45平方米的三角形菜地,它的高是15米,它的底是( )米;一个梯形的面积是18平方厘米,上底与下底的和是9厘米,高是( )厘米。
11.如图所示,长方形与平行四边形部分重叠,已知梯形甲的面积是35cm2。则梯形乙的面积是( )cm2。
三、计算题
12.计算下面图形的面积。
13.求下面图形的面积。(单位:cm)
四、作图题
14.如图每个小方格边长1厘米,请在方格中画出面积是12平方厘米的平行四边形,再画出与它面积相等的三角形和梯形各一个。
五、解答题
15.用两个完全一样的梯形拼成一个平行四边形(如下图),每个梯形的面积是多少平方厘米?
16.如图,长方形被分成了一个三角形和一个梯形。已知三角形的面积比梯形少180平方厘米,求三角形和梯形的面积。
17.一个梯形的下底长是18厘米,如果把上底延长12厘米,就成了一个平行四边形,面积增加了24平方厘米。那么原来梯形的面积是多少平方厘米?
18.一个梯形的上底是10厘米,如果把上底延长5厘米就变成了一个面积120平方厘米的平行四边形,原来梯形的面积是多少平方厘米?
19.绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如图),草坪的面积是多少平方米?
20.一个牧场的形状如图。
这个牧场的面积是多少平方米?是多少公顷?
21.实验小学的报告厅一共有20排座位。其中第一排有10个座位,第二排有12个座位,后面每一排的座位数都比前一排多2个。实验小学的报告厅一共有多少个座位?
22.王老师请广告公司制作一块梯形广告牌,这块广告牌的上底是3.6米,下底是8.4米,高是4米。如果这个广告公司制作广告牌每平方米收费25元,那么王老师要付给这个广告公司多少元?
23.如下图,梯形的面积是64平方厘米,阴影部分的面积是多少?
24.如图,两个完全相同的直角梯形重叠在一起,求阴影部分的面积。(单位:厘米)
25.如图所示,两个完全一样的直角三角形重叠在一起,求阴影部分的面积。(单位:cm)
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】结合题意观察图可知:这块地的面积也就是梯形的面积,梯形的面积=(上底+下底)×高÷2,用栅栏总长度120米减去梯形的高40米,即可求出梯形的上底+下底的长度。据此解答。
【详解】(120-40)×40÷2
=80×40÷2
=3200÷2
=1600(平方米)
所以,这块地的面积是1600平方米。
故答案为:B
2.C
【分析】借鉴梯形面积公式,圆木总根数=(上层根数+下层根数)×层数÷2,总层数=下层根数-上层根数+1,据此列式计算。
【详解】18-7+1=12(层)
(7+18)×12÷2
=25×12÷2
=150(根)
这堆圆木共有150根。
故答案为:C
3.B
【分析】观察图形可知,甲图是长方形面积减去空白三角形面积,乙图面积是平行四边形面积减去空白三角形面积;根据长方形面积公式:面积=长×宽;平行四边形面积公式:面积=底×高;长方形的宽=平行四边形的底;长方形的长=平行四边形的高,由此可知,长方形面积=平行四边形面积;由于空白三角形是公共部分的面积,所以甲的面积等于乙的面积,据此解答。
【详解】根据分析可知,如下图,梯形甲的面积等于乙图面积。
故答案为:B
【点睛】明确平行四边形面积与长方形面积的关系是解答本题的关键。
4. 12 48
【分析】根据题意,把梯形转化成平行四边形,那么梯形的面积等于平行四边形的面积。
观察图形可知,平行四边形的底等于AB的2倍,平行四边形的高等于梯形高的一半,根据平行四边形的面积=底×高,求出平行四边形的面积,也是原来梯形的面积。
【详解】平行四边形的底:6×2=12(厘米)
平行四边形的高:8÷2=4(厘米)
面积:12×4=48(平方厘米)
那么转化后平行四边形的底是12厘米,原来梯形的面积是48平方厘米。
5. 7.2 21.6 43.2
【分析】根据公式:梯形的高=面积×2÷(上底+下底),即可求出梯形的高;阴影部分是个三角形,根据公式:三角形的面积=底×高÷2,即可求出阴影部分的面积;这个梯形内最大的平行四边形的底与梯形的上底相等,高与梯形的高相等,根据公式:平行四边形的面积=底×高,即可求出平行四边形的面积。
【详解】54×2÷(6+9)
=54×2÷15
=108÷15
=7.2(厘米);
6×7.2÷2
=43.2÷2
=21.6(平方厘米);
6×7.2=43.2(平方厘米)。
即梯形的高是7.2厘米,阴影部分的面积是21.6平方厘米,平行四边形的面积是43.2平方厘米。
6. 0.126 0.294
【分析】看图,三角形和梯形的高,与平行四边形的高相等。三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,据此列式求出这个三角形和梯形的面积。
【详解】0.42×0.6÷2
=0.252÷2
=0.126(平方分米)
(0.7+0.7-0.42)×0.6÷2
=0.98×0.6÷2
=0.294(平方分米)
所以,三角形的面积是0.126平方分米,梯形的面积是0.294平方分米。
7.60
【分析】根据题意,梯形的高不变,把它的上底延长5厘米,下底缩短5厘米,则梯形的上、下底之和不变,根据梯形的面积=(上底+下底)×高÷2可知,梯形的面积不变。
【详解】梯形的上底延长5厘米,下底缩短5厘米后,那么:
梯形的面积=(上底+5+下底-5)×高÷2=(上底+下底)×高÷2
即梯形的上、下底之和不变,高不变,则梯形的面积不变,所以梯形的面积是60平方厘米。
8.110
【分析】
最上层有5根,最下层有15根,每相邻两层相差1根,共有11层,则可以看成一个梯形,按照梯形的面积的面积求出钢管的个数。梯形的面积=(上底+下底)×高÷2,上底是5,下底是15,一共有11层,则高是11。
【详解】(5+15)×11÷2
=20×11÷2
=110(根)
则这堆钢管共有110根。
9.164
【分析】因为每增加一层根数就减少1根,所以最上层的根数等于最下层的根减去层数加1,据此前项最上层的根数,然后根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】(24-8+1+24)×8÷2
=(16+1+24)×8÷2
=(17+24)×8÷2
=41×8÷2
=328÷2
=164(根)
这堆钢管一共有164根。
10. 6 4
【分析】(1)三角形的面积=底×高÷2,则三角形的底=三角形的面积×2÷高。
(2)梯形的面积=(上底+下底)×高÷2,则梯形的高=梯形的面积×2÷(上底+下底)。
【详解】45×2÷15
=90÷15
=6(米)
则三角形的底是6米。
18×2÷9
=36÷9
=4(厘米)
则梯形的高是4厘米。
11.35
【分析】根据图示可知,长方形与平行四边形等底等高,所以长方形的面积等于平行四边形的面积。S甲=S长方形-S空白,S乙=S平行四边形-S空白,所以梯形乙的面积和梯形甲的面积相等,是35cm2。
【详解】根据分析,梯形乙的面积和梯形甲的面积相等,是35cm2。
12.84cm2;54m2;192cm2
【分析】(1)根据平行四边形的面积=底×高,代入数据计算即可求解。
(2)观察图形可知,组合图形的面积=三角形的面积+梯形的面积,根据三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算即可求解。
(3)如下图,补齐缺口处,那么组合图形的面积=梯形的面积-正方形的面积,根据梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,代入数据计算即可求解。
【详解】(1)8×10.5=84(cm2)
平行四边形的面积是84cm2。
(2)9×4÷2+(9+3)×6÷2
=36÷2+12×6÷2
=18+36
=54(m2)
组合图形的面积是54m2。
(3)(8+24)×(8+8)÷2-8×8
=32×16÷2-64
=256-64
=192(cm2)
组合图形的面积是192cm2。
13.700cm2;282cm2;64cm2
【分析】(1)组合图形的面积=梯形的面积+正方形的面积,根据梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,代入数据计算求解。
(2)组合图形的面积=平行四边形的面积+三角形的面积,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,代入数据计算求解。
(3)组合图形的面积=长方形的面积-梯形的面积,根据长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,代入数据计算求解。
【详解】(1)(20+40)×10÷2+20×20
=60×10÷2+400
=300+400
=700(cm2)
组合图形的面积是700cm2。
(2)12×16+20×9÷2
=192+90
=282(cm2)
组合图形的面积是282cm2。
(3)10×8-(6+10)×2÷2
=80-16×2÷2
=80-16
=64(cm2)
组合图形的面积是64cm2。
14.见详解
【分析】每个图形的面积是12平方厘米,将12拆分成6×2,根据平行四边形的面积公式,用6厘米当作平行四边形的底,2厘米当平行四边形的高;根据三角形的面积=底×高÷2,将12×2拆分成3×8,用8厘米当三角形的底,3厘米当三角形的高;根据梯形的面积=(上底+下底)×高÷2,将12×2拆分成6×4,再将6拆分成2+4,然后用2厘米当梯形的上底,4厘米当梯形的下底,4厘米当梯形的高,据此画图。
【详解】如图:
(答案不唯一)
15.320平方厘米
【分析】根据题意,用两个完全一样的梯形拼成一个底为40厘米、高为16厘米的平行四边形,根据平行四边形的面积=底×高,求出平行四边形的面积,也就是两个梯形的面积,再除以2,即是每个梯形的面积。
【详解】40×16÷2
=640÷2
=320(平方厘米)
答:每个梯形的面积是320平方厘米。
16.210平方厘米;390平方厘米
【分析】通过做辅助线可知,梯形比三角形多的就是小长方形的面积,根据长方形面积=长×宽,可以求出小长方形的宽,也就是梯形的上底。三角形的底=30厘米-小长方形的宽,三角形的高是20厘米。
根据公式:三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】
如图所示:
180÷20=9(厘米)
30-9=21(厘米)
21×20÷2
=420÷2
=210(平方厘米)
(9+30)×20÷2
=39×20÷2
=780÷2
=390(平方厘米)
答:三角形的面积是210平方厘米,梯形的面积是390平方厘米。
17.48平方厘米
【分析】由题意可知:增加部分是一个三角形,其面积和底已知,于是即可求出三角形的高,也就等于知道了梯形的高,进而依据梯形的面积公式即可求解。
【详解】24×2÷12
=48÷12
=4(厘米)
(18-12+18)×4÷2
=24×4÷2
=48(平方厘米)
答:梯形的面积是48平方厘米。
18.100平方厘米
【分析】读题可知,平行四边形的底=梯形下底,平行四边形的高=梯形的高,梯形上底+5厘米=下底,根据平行四边形的高=面积÷底,梯形面积=(上底+下底)×高÷2,列式解答即可。
【详解】10+5=15(厘米)
120÷15=8(厘米)
(10+15)×8÷2
=25×8÷2
=100(平方厘米)
答:原来梯形的面积是100平方厘米。
19.512平方米
【分析】由图可知,草坪的面积=梯形草坪的面积-长方形的花坛,根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据解答即可。
【详解】(20+36)×20÷2
=56×20÷2
=1120÷2
=560(平方米)
12×4=48(平方米)
560-48=512(平方米)
答:草坪的面积是512平方米。
20.40000平方米;4公顷
【分析】牧场的面积=两个梯形的面积,根据梯形的面积=(上底+下底)×高÷2,代入数据,即可求出牧场的面积,再根据1公顷=10000平方米,低级单位化高级单位除以进率即可解答。
【详解】(30+220)×(230-150)÷2
=250×80÷2
=20000÷2
=10000(平方米)
(180+220)×150÷2
=400×150÷2
=60000÷2
=30000(平方米)
10000+30000=40000(平方米)
40000平方米=4公顷
答:这个牧场的面积是40000平方米,是4公顷。
21.580个
【分析】
后面每一排的座位数都比前一排多2个,共有20排座位,因此最后一排座位数=第一排座位数+2×(总排数-1),座位的摆放类似一个梯形,根据梯形面积公式,座位总数=(第一排座位数+最后一排座位数)×排数÷2,据此列式解答。
【详解】最后一排座位数:10+2×(20-1)
=10+2×19
=10+38
=48(个)
座位总数:(10+48)×20÷2
=58×20÷2
=580(个)
答:实验小学的报告厅一共有580个座位。
22.600元
【分析】根据梯形面积=(上底+下底)×高÷2,求出广告牌面积,广告牌面积×每平方米收费=要付的钱数,据此列式解答。
【详解】(3.6+8.4)×4÷2×25
=12×4÷2×25
=24×25
=600(元)
答:王老师要付给这个广告公司600元。
23.52平方厘米
【分析】阴影部分是底是13厘米,高等于梯形高的三角形;根据梯形的面积公式:面积=(上底+下底)×高÷2,高=面积×2÷(上底+下底),代入数据,求出梯形的高,也就是阴影部分三角形的高;再根据三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】64×2÷(3+13)
=128÷16
=8(厘米)
13×8÷2
=104÷2
=52(平方厘米)
答:阴影部分面积是52平方厘米。
24.33平方厘米
【分析】如图所示,因为空白a是两个直角梯形的公共部分,去掉公共部分,则剩下的部分底面积也相等,即空白b和阴影部分的面积相等,而空白b的下底已知,高就是3厘米,上底可以求出,于是利用梯形的面积公式即(上底+下底)×高÷2可求解。
【详解】(12-2+12)×3÷2
=22×3÷2
=66÷2
=33(平方厘米)
答:阴影部分的面积是33平方厘米。
【点睛】解答此题的关键是明白阴影部分的面积就等于空白b的面积,从而可以利用梯形面积公式求解。
25.18cm2
【分析】阴影部分面积=大三角形的面积先减去一个小三角形面积,左边梯形面积也是由大三角形面积减去小三角形面积,所以梯形面积与阴影部分面积相等,根据梯形面积公式:(上底+下底)×高÷2,上底是(6-3)cm,下底是6cm,高是4cm,代入数据,即可解答。
【详解】(6-3+6)×4÷2
=(3+6)×4÷2
=9×4÷2
=36÷2
=18(cm2)
答:阴影部分面积是18cm2。
【点睛】本题考查组合图形面积的计算,根据图形的特征,通过转化的方法,将阴影部分面积转化为梯形,从而求出面积。
