【举一反三题型总结】苏教版五上 第二单元 简单的组合图形和不规则图形的面积(知识点+例题+变式题)
文档属性
| 名称 | 【举一反三题型总结】苏教版五上 第二单元 简单的组合图形和不规则图形的面积(知识点+例题+变式题) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 19:15:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
组合图形和不规则图形的面积知识点梳理+题型总结
联系已学知识认识简单的组合图形,能把组合图形分解成已经学过的平面图形并计算出面积。
运用数方格法对不规则图形的面积进行估算,初步体会化难为易、化繁为简的解题策略和数学方法。
能用多种策略解决问题,激发探究数学问题的积极性。
1、组合图形的面积
在计算组合图形的面积时,通常先把组合图形分割成已学过的简单图形,分别计算出各个简单图形的面积,再把它们加起来,也可以把组合图形补成一个简单的图形,再用补成的简单图形的面积减去补上的简单图形的面积。
2、不规则图形的面积
求不规则图形的面积,可以用数方格法进行估计。估计时,先数整格的,再数不满整格的,不满整格的按半格计算。
重难点一:用分割和添补法解决简单组合图形的问题
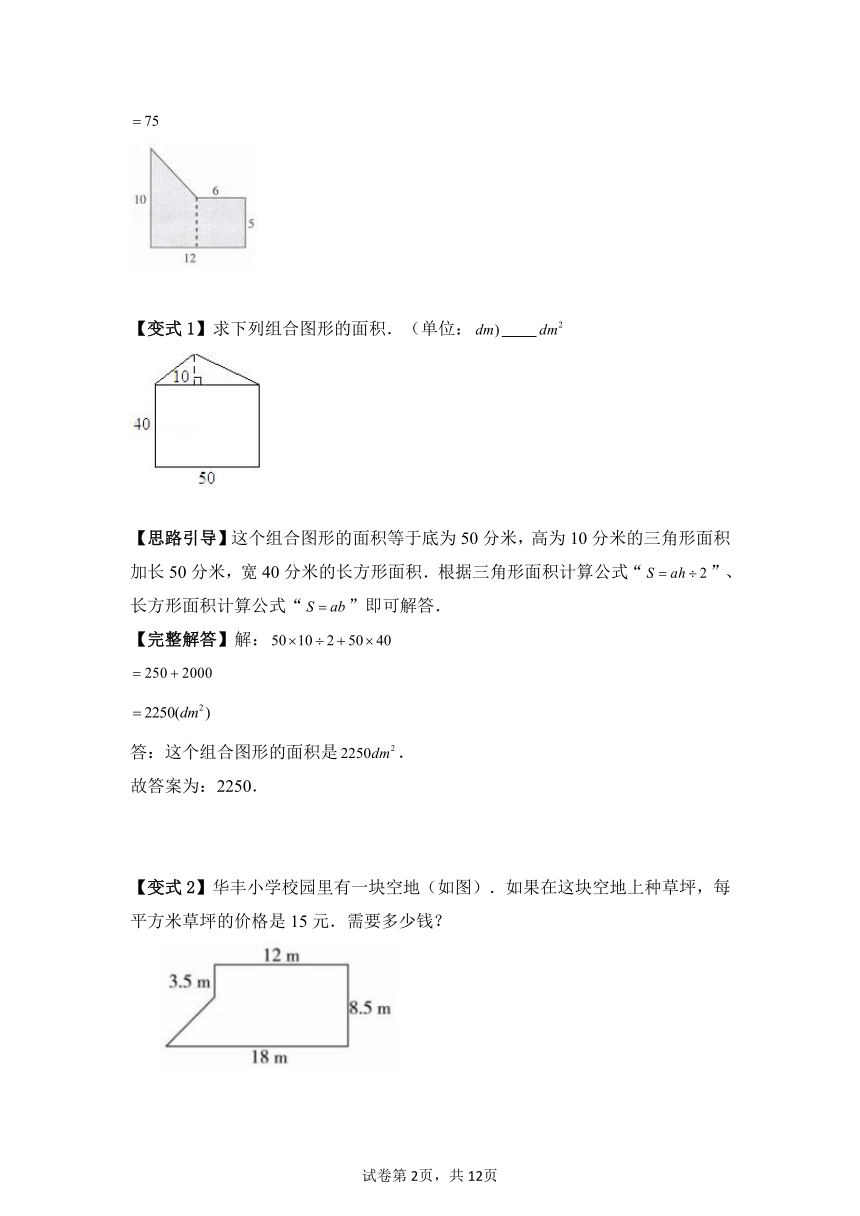
【例题】 求下面各图形的面积。(单位:厘米)
梯形的高:
【变式1】求下列组合图形的面积.(单位:
【思路引导】这个组合图形的面积等于底为50分米,高为10分米的三角形面积加长50分米,宽40分米的长方形面积.根据三角形面积计算公式“”、长方形面积计算公式“”即可解答.
【完整解答】解:
答:这个组合图形的面积是.
故答案为:2250.
【变式2】华丰小学校园里有一块空地(如图).如果在这块空地上种草坪,每平方米草坪的价格是15元.需要多少钱?
【思路引导】如图,,这块空地的面积长方形的面积三角形的面积,长方形的长是,宽是;三角形的底是,高是,根据长方形和三角形的面积公式,求出这块地的面积,然后再根据乘法的意义,乘上15即可.
【完整解答】解:
(平方米)
(元
答:需要1755元钱.
【变式3】 如图,在四边形ABCD中,∠CBA和∠CDA都是直角,AD=10厘米,BC=6厘米,∠BAD=45°,求四边形ABCD的面积。
【完整解答】解:,
,
(平方厘米),
答:四边形的面积是20平方厘米.
重难点二:不规则图形面积的计算
【例题】下面是一个湖泊的平面图(每个小方格表示1公顷)。你能估计这个湖泊的面积大约是多少公顷吗?
①只数整格的,实际面积比数出的结果要大一些。
②把不满整格的也当作整格数,实际面积比数出的要小一些。
答案:整格的有55个,面积是55公顷。不满整格的有36个,面积大约是18公顷。
55+18=73(公顷)
答:这个湖泊的面积大约是73公顷。
分析:求不规则图形的面积,可以用数方格的方法进行估算。估算时,先数整格
的,再数不满整格的,不满整格的按半格计算,最后把两个结果相加,这样得到
的近似数最接近实际结果,比较合理。
【变式题】数一数,算一算。(每个小方格表示1平方厘米)
(1)如下图,一朵花所占的格子中,整格的有( )个,不满整格的有( )个,面积大约是( )平方厘米。
(2)如下图,一片树叶所占的格子中,整格的有( )个,不满整格的有( )个,面积大约是( )平方厘米。
答案:(1)6,16,14
(2)30,26,43
一、选择题
1.下图中树叶的面积大约是( )平方厘米。
A.26 B.56 C.39 D.22
2.如图,平行四边形的面积是18平方厘米,那么长方形的面积( )。
A.大于18平方厘米 B.等于18平方厘米
C.小于18平方厘米 D.无法比较
3.如图中阴影甲的面积比阴影乙的面积大( )。
A.6平方厘米 B.8平方厘米
C.4平方厘米 D.10平方厘米
二、填空题
4.下图平行四边形的面积是16平方厘米,涂色部分的面积是( )。
三、计算题
5.求下面图形的面积。
6.计算下面图形的面积。
7.计算下面图形中涂色部分的面积。(单位:厘米)
8.计算下面图形的面积。
9.计算下面图形涂色部分的面积。(单位:厘米)
(1)
(2)
10.如下图所示,求阴影部分的面积。(单位:米)
11.求彩色部分的面积(单位:厘米)。
12.如图,四边形ACDB和四边形DEFG都是正方形,已知厘米,厘米,求三角形BCF的面积。
13.计算下面图形阴影部分的面积。(单位:厘米)
14.求阴影部分面积。(单位:厘米)
四、解答题
15.如图,大正方形的边长是14厘米,小正方形的边长是10厘米。求阴影部分的面积。
16.如图,一块长方形草地,长方形的长是16米,宽是12米,中间铺了两条石子路(如图示意),那么草地部分面积有多少平方米?
17.一块近似平行四边形的草坪,被一条长方形的石子路分成了两块(如图)。已知平行四边形的底是39米,小路宽1米。这个草坪的面积是多少平方米?
18.王亮家要粉刷一面墙(如图,中间是窗户)。(单位:米)
(1)请你帮他算一算,要粉刷多大的面积?
(2)如果每平方米要用涂料2千克,一共要买多少千克涂料?
19.数学实践活动课中,李明把一张平行四边形的纸剪成一个三角形和一个梯形(如下图)。已知三角形的面积和梯形的面积相差18平方厘米,剪出的梯形面积是多少平方厘米?
20.如图所示,长方形的长和宽分别是8厘米和6厘米,阴影部分的总面积是16平方厘米。求四边形ABCD的面积。
21.已知一个四边形中∠B=∠D=90°,∠C=45°,AD=4cm,试求出这个四边形的面积是多少?(单位:厘米)
22.如下图所示,四边形ABCD周长为18cm,图中P点到四边形ABCD的距离相同为3cm,求四边形ABCD的面积。
23.在平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,求平行四边形ABCD面积。
24.如下图,一个长方形被一些直线分成若干个小块,已知三角形ADG的面积是11平方厘米,三角形BCH的面积是23平方厘米,求四边形EGFH的面积。
25.如图,已知三角形ABC中,DC=2BD,CE=4AE。阴影部分面积是20平方厘米,求三角形ABC的面积。
26.如图,四边形ABCD是边长为8厘米的正方形,梯形AEBD的两条对角线交于O,三角形AOE的面积比三角形BOD的面积小16平方厘米。求梯形AEBD的面积。
27.图中两个正方形的边长分别是10厘米和8厘米,求阴影部分的面积?
28.四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。三角形CDH的面积是多少平方厘米?
29.如图,平行四边形BCEF中,厘米,直角三角形中,厘米,阴影部分面积比三角形ADH的面积大8平方厘米。求AH长多少厘米?
30.在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)
31.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?
32.如图平行四边形ABCD的边BC长为10厘米,直角三角形BCE的直角边CE长为8厘米.已知两块阴影部分的面积之和比三角形EFG的面积大10平方厘米.CF长是多少厘米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】先数完整的格子数量,再数不足一格的数量,不足一格的按半格计算,最后求和即可。
【详解】整格有22个,半格有34个。
22+34÷2
=22+17
=39(平方厘米)
下图中树叶的面积大约是39平方厘米。
故答案为:C
【点睛】熟练掌握数格法求不规则图形的面积的方法是解答本题的关键。
2.B
【分析】把长方形沿对角线分成两个完全一样的三角形,每个三角形的底等于平行四边形的底,每个三角形的高等于平行四边形的高,因为等底等高的平行四边形的面积是三角形面积的2倍,所以这两个三角形(阴影部分)的面积等于平行四边形,也就是长方形的面积等于平行四边形的面积;据此解答即可。
【详解】因为等底等高的平行四边形的面积是三角形面积的2倍,所以这两个三角形(阴影部分)的面积等于平行四边形,也就是长方形的面积等于平行四边形的面积。
故答案为:B
【点睛】此题考查的目的是理解掌握等底等高的三角形与平行四边形面积之间的关系及应用,等底等高的平行四边形与长方形面积之间的关系及应用。
3.A
【分析】求阴影甲与阴影乙的面积差,实际上是求大三角形与正方形的面积差,将数据代入三角形和正方形的面积
【详解】(6+8)×6÷2-6×6
=14×6÷2-36
=42-36
=6(平方厘米)。
【点睛】本题的关键是将阴影部分的面积进行转化。
4.8平方厘米
【分析】根据观察图可知涂色部分是一个三角形,该三角形和平行四边形等底等高,所以涂色部分的面积是该四边形面积的一半,据此分析即可。
【详解】由分析可知,涂色部分的面积是平行四边形面积的一半,
所以涂色部分面积为:
16÷2=8(平方厘米)
【点睛】本题主要考查了等底等高的平行四边形和三角形的面积关系,即等底等高的三角形的面积是平行四边形的一半,要求学生熟练掌握并且会灵活运用。
5.143cm2
【分析】由图可知,图形的面积=三角形的面积+长方形的面积,根据三角形的面积=底×高÷2,长方形的面积=长×宽,代入数据进行解答即可。
【详解】(8+7)×(20-14)÷2
=15×6÷2
=90÷2
=45(cm2)
45+7×14
=45+98
=143(cm2)
图形的面积是143cm2。
6.84cm2;54m2;192cm2
【分析】(1)根据平行四边形的面积=底×高,代入数据计算即可求解。
(2)观察图形可知,组合图形的面积=三角形的面积+梯形的面积,根据三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算即可求解。
(3)如下图,补齐缺口处,那么组合图形的面积=梯形的面积-正方形的面积,根据梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,代入数据计算即可求解。
【详解】(1)8×10.5=84(cm2)
平行四边形的面积是84cm2。
(2)9×4÷2+(9+3)×6÷2
=36÷2+12×6÷2
=18+36
=54(m2)
组合图形的面积是54m2。
(3)(8+24)×(8+8)÷2-8×8
=32×16÷2-64
=256-64
=192(cm2)
组合图形的面积是192cm2。
7.42平方厘米;26平方厘米
【分析】(1)涂色部分的面积=平行四边形的面积-三角形的面积。根据平行四边形的面积=底×高,用8×6求出平行四边形的面积(48平方厘米);三角形的底是8-3-2=3(厘米),根据三角形的面积=底×高÷2,用3×4÷2求出三角形的面积(6平方厘米);用48-6求出涂色部分的面积。
(2)如下图,涂色部分的面积=正方形ABCD的面积+正方形CEFG的面积-三角形ABD的面积-三角形BEF的面积。根据正方形的面积=边长×边长,用8×8求出正方形ABCD的面积(64平方厘米),用6×6求出正方形CEFG的面积(36平方厘米);根据三角形的面积=底×高÷2,用8×8÷2求出三角形ABD的面积(32平方厘米),用(8+6)×6÷2求出三角形BEF的面积(42平方厘米);最后用64+36-32-42求出涂色部分的面积。
【详解】8×6-(8-3-2)×4÷2
=48-3×4÷2
=48-12÷2
=48-6
=42(平方厘米)
涂色部分面积是42平方厘米。
8×8+6×6-8×8÷2-(8+6)×6÷2
=64+36-32-14×6÷2
=100-32-84÷2
=68-42
=26(平方厘米)
涂色部分面积是26平方厘米。
8.1050cm2;42cm2
【分析】第一个图形是平行四边形,其中一条边是30cm,另在这条边上的高是35cm,根据平行四边形面积=底×高,计算得出面积;第二个图形是一个梯形和一个长方形组合起来的图形,根据梯形面积=(上底+下底)×高÷2,长方形面积=长×宽,两个面积相加得出答案。
【详解】第一个图形面积为:(cm2);
第二个图形面积为:
(cm2)
9.(1)36平方厘米
(2)33.75平方厘米
【分析】(1)观察图形可得:涂色部分的面积=底为12厘米、高为6厘米的平行四边形的面积-底为12厘米、高为6厘米的三角形的面积,然后再根据平行四边形的面积公式S=ah、三角形的面积公式S=ah÷2进行解答。
(2)观察图形可得:涂色部分的面积=长为5厘米、宽为2.5厘米的长方形的面积+上底为2.5厘米、下底为6厘米、高为(10-5)厘米的梯形的面积,然后再根据长方形的面积公式S=ab、梯形的面积公式S=(a+b)h÷2进行解答。
【详解】(1)12×6-12×6÷2
=72-36
=36(平方厘米)
涂色部分的面积是36平方厘米。
(2)5×2.5+(2.5+6)×(10-5)÷2
=12.5+8.5×5÷2
=12.5+21.25
=33.75(平方厘米)
涂色部分的面积是33.75平方厘米。
10.31.5平方米
【分析】由题意可以看出,阴影部分面积等于边长是9米的正方形面积的一半加上边长是6米的正方形面积,再减去底为(9+6)米,高为6米的三角形面积.根据正方形的面积计算公式“S=a2”及三角形面积计算公式“S=ab”即可求出阴影部分面积。
【详解】9×9×+6×6-×(9+6)×6
=81×+36-×15×6
=40.5+36-45
=76.5-45
=31.5(平方米)
阴影部分面积是31.5平方米。
11.13.5平方厘米
【分析】观察图形可知,彩色部分是一个三角形,三角形的底是(5+4)厘米,高是3厘米。三角形的面积=底×高÷2,据此代入数据计算。
【详解】(5+4)×3÷2
=9×3÷2
=13.5(平方厘米)
则彩色部分的面积是13.5平方厘米。
12.32平方厘米
【分析】观察图形可知,三角形BCF的面积等于正方形ACDB、正方形DEFG和三角形BGF的面积和减去三角形ACB和三角形CEF的面积,据此解题即可。
【详解】[8×8+6×6+6×(8-6)÷2]-[8×8÷2+(8+6)×6÷2]
=[8×8+6×6+6×2÷2]-[8×8÷2+14×6÷2]
=[64+36+6]-[32+42]
=106-74
=32(平方厘米)
三角形BCF的面积是32平方厘米。
13.33.75平方厘米;30平方厘米
【分析】由图可知,此图可以分割成如下图所示图形,阴影面积=长方形面积+三角形面积,根据长方形面积计算公式S=ab和三角形的面积公式S=ah÷2即可求解;
由图可知,阴影面积=大三角形面积-小三角形面积,利用三角形的面积公式S=ah÷2即可求解。
【详解】2.5×10+(6-2.5)×(10-5)÷2
=25+3.5×5÷2
=25+8.75
=33.75(平方厘米)
10×(10+6)÷2-10×10÷2
=10×16÷2-50
=80-50
=30(平方厘米)
14.64平方厘米;42平方厘米;50平方厘米
【详解】图1阴影部分的面积:
16×16-(16×16÷2+16×8÷2)
=256-(128+64)
=64(平方厘米)
图2阴影部分的面积:
10×10+8×8-10×10÷2-(10+8)×8÷2
=164-50-72
=42(平方厘米)
设图3小正方形的边长为a,则阴影部分的面积:
×10×10+×(a+10)×a-×(a+10)×a
=×10×10
=50(平方厘米)
15.98平方厘米。
【分析】
通过观察图形可知,如图:阴影部分的面积等于长(14+10)厘米,宽14厘米的长方形的面积减去空白部分3个三角形的面积(1号三角形的底和高都为14厘米;2号三角形的底为14+10=24厘米,高为10厘米;3号三角形的底为10厘米,高为14-10=4厘米),根据长方形的面积公式;S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】(14+10)×14-14×14÷2-(14+10)×10÷2-(14-10)×10÷2
=24×14-196÷2-24×10÷2-4×10÷2
=336-98-120-20
=238-120-20
=118-20
=98(平方厘米)
答:阴影部分的面积是98平方厘米。
16.140平方米
【分析】用平移的方法,把分割开的四块草地拼成一个新的长方形,这个新的长方形的长为(16-2)米、宽为(12-2)米,根据长方形的面积=长×宽,即可求出草地部分的面积。
【详解】(16-2)×(12-2)
=14×10
=140(平方米)
答:草地部分面积有140平方米。
17.912平方米
【分析】这个草坪的面积等于底为39米,高为24米的平行四边形的面积减去一个长为24米,宽为1米的长方形石子路的面积,分别利用平行四形和长方形的面积公式,代入数据即可求出这个草坪的面积。
【详解】39×24-1×24
=936-24
=912(平方米)
答:这个草坪的面积是912平方米。
【点睛】此题主要考查组合图形的面积的计算方法,熟练运用平行四形和长方形的面积公式解决问题。
18.(1)17平方米
(2)34千克
【分析】(1)根据墙的示意图,粉刷部分的面积是上面的三角形面积加下面的正方形面积减去长方形(窗)的面积;
(2)用每平方米用的涂料2千克乘粉刷面积就可以求出一共要买多少千克涂料,据此解答。
【详解】(1)(1+4+1)×1÷2+4×4-1×2
=3+16-2
=17(平方米)
答:要粉刷多大的面积是17平方米。
(2)2×17=34(千克)
答:一共要买34千克涂料。
【点睛】考查组合图形面积的计算及解决实际问题。
19.39平方厘米
【分析】根据平行四边形面积公式:面积=底×高;代入数据,求出平行四边形面积;三角形面积+梯形面积=平行四边形面积;三角形面积和梯形面积相差18平方厘米,即三角形面积+三角形面积+18=平行四边形面积,三角形面积=(平行四边形面积-18)÷2,据此求出三角形面积,进而求出梯形面积。
【详解】(10×6-18)÷2
=(60-18)÷2
=42÷2
=21(平方厘米)
21+18=39(平方厘米)
答:剪出的梯形面积是39平方厘米。
【点睛】利用平行四边形面积公式,根据三角形面积与梯形面积之间的关系,三角形、梯形和平行四边形面积之间的关系,进行解答。
20.4平方厘米
【分析】根据三角形的面积公式得出△AEF和△AGH的面积和正好等于长方形EFGH的面积的面积的一半,根据长方形的面积求出△ECH的面积,结合图形求出即可。
【详解】△AEF和△AGH的面积和正好等于长方形EFGH的面积的面积的一半,即
×8×6
=4×6
=24(平方厘米)
四边形EFGH是长方形,△ECH的面积是长方形面积的
×8×6
=2×6
=12(平方厘米)
所以,四边形ABCD的面积是:
12-(24 -16)
=12-8
=4(平方厘米)
答:四边形ABCD的面积是4平方厘米。
【点睛】本题考查了三角形的面积和正方形的面积的应用,主要考查学生能否根据图形把求不规则图形的面积转化成求规图形的面积。
21.42平方厘米
【分析】延长BA和CD,相较于一点于E,那么四边形的面积=三角形BCE的面积-三角形ADE的面积。
【详解】
如图所示,∠E=45°,所以三角形AED是等腰直角三角形,AD=DE=4cm,三角形BCE也是等腰直角三角形,BC=BE=10cm。所以四边形的面积为:
10×10÷2-4×4÷2
=50-8
=42(平方厘米)
【点睛】此题考查了组合图形的面积计算,运用了填补法。认真观察图形解答即可。
22.27平方厘米
【分析】根据题意,把P点与ABCD四个点连接,把四边形ABCD分成四个三角形,如图,三角形APB,三角形BPC,三角形CPD,三角形DPA,根据三角形面积公式:底×高÷2,三角形APB的面积=AB×3÷2;三角形BPC的面积=BC×3÷2;三角形CPD的面积=CD×3÷2;三角形DPA的面积=AD×3÷2,四个三角形相加,就是四边形ABCD的面积,即:AB×3÷2+BC×3÷2+CD×3÷2+DA×3÷2,再化为:(AB+BC+CD+DA)×3÷2,即四边形ABCD的周长×3÷2 代入数据,即可解答。
【详解】18×3÷2
=54÷2
=27(平方厘米)
答:四边形ABCD的面积是27平方厘米。
【点睛】解答本题的关键是把四边形平成四个高是3厘米的三角形,再利用三角形面积公式,求出四边形的面积。
23.54平方厘米
【分析】根据题意可知,AE=EF=EB,由此可知三角形AEG=三角形EFG=三角形FBG,三角形ABG的面积=6×3=18平方厘米;AG=2CG,由此可知三角形CBG的面积=三角形ABG面积÷2,即三角形CBG的面积=18÷2=9平方厘米,三角形ABC的面积=三角形ABG的面积+CBG的面积=18+9=27平方厘米,平行四边形ABCD的面积=三角形ABC的面积×2,用27×2,即可解答。
【详解】三角形ABG的面积:
6×3=18(平方厘米)
三角形CBG的面积:
18÷2=9(平方厘米)
三角形ABC的面积:
18+9=27(平方厘米)
平行四边形ABCD的面积:
27×2=54(平方厘米)
答:平行四边形ABCD的面积是54平方厘米。
【点睛】解答本题的关键是利用三角形等底等高,求出三角形面积,再利用三角形面积求出平行四边形面积。
24.34平方厘米
【分析】由题意可知:S△ADE+S△ECB=S△DCF,等式的两边分别去掉公共部分,即S△DGE+S△EHC,则剩余的部分的面积仍然相等,即S△ADG +S△ADG =S四边形EGFH,据此代入数据即可求解。
【详解】因为S△ADE+S△ECB=S△DCF
等式的两边分别去掉公共部分,即S△DGE+S△EHC
即S△ADG +S△BCH =S四边形EGFH
11+23=34(平方厘米)
答:求四边形EGFH的面积是34平方厘米。
【点睛】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半。
25.150平方厘米
【分析】如果两个三角形的高相等,那么这两个三角形的面积比等于它们底的比,先求出三角形DCE的面积,再求三角形ABD的面积然后加上阴影部分面积即可求大三角形的面积。
【详解】由题意可知:三角形DCE面积=三角形ADE面积×4
20×4=80(平方厘米)
三角形ADB面积:
三角形ADC面积×
=(三角形ADE面积+三角形DCE面积)×
=(20+80)×
=100×
=50(平方厘米)
三角形ABC面积=50+80+20=150(平方厘米)
答:三角形ABC的面积是150平方厘米。
【点睛】此题关键是利用“如果两个三角形的高相等,那么这两个三角形的面积比等于它们底的比”求解。
26.48平方厘米
【分析】在梯形AEBD中,三角形ABD和三角形EBD是同底等高,所以三角形ABD面积=三角形EBD面积,进而求出三角形AOD面积=三角形EBO的面积;因为三角形BOD面积比三角形AOE的面积大16平方厘米,因此三角形BOD面积+三角形AOD的面积(即三角形ABD的面积)-(三角形EBO的面积+三角形AOE的面积)=16,由于三角形ABD的面积=正方形ABCD面积的一半,所以三角形EBO的面积+三角形AOE的面积=三角形ABD的面积-16平方厘米,根据三角形面积公式:底×高÷2,三角形ABD的面积=8×8÷2=32;三角形EBO的面积+三角形AOE的面积=32-16=16,梯形AEBD的面积=三角形EOB的面积+三角形AOE的面积+三角形ABD的面积,即32+16=48平方厘米,据此解答。
【详解】三角形AOE的面积+三角形EBO的面积:
8×8÷1-16
=64÷2-16
=32-16
=16(平方厘米)
梯形面积:
32+16=48(平方厘米)
答:梯形AEBD的面积是48平方厘米。
【点睛】解答本题关键明确等底等高的三角形面积相等,利用等量代换的方法进行解答。
27.50平方厘米
【分析】如图,要求阴影部分的面积,可以先求三角形BCD和梯形CEFD的面积,然后减去下面三角形BEF的面积,据此解答。
【详解】S△BCD+S梯形CEFD-S△BEF=阴影面积
10×10÷2+(8+10)×8÷2-8×(10+8)÷2
=50+72-72
=50(平方厘米)
答:阴影部分的面积是50平方厘米。
【点睛】此题主要考查学生利用灵活转化的思想球图形面积的能力。
28.7平方厘米
【分析】如下图所示,连接FD,则三角形FDC和三角形AFD等底等高,则二者的面积相等,分别减去公共部分三角形FHD,则剩余部分的面积仍然相等,即三角形AFH和三角形CDH的面积相等,据此即可得解。
【详解】连接FD,则三角形FDC和三角形AFD等底等高,则二者的面积相等,分别减去公共部分三角形FHD,则剩余部分的面积仍然相等;
即三角形AFH和三角形CDH的面积相等,所以三角形CDH的面积也等于7平方厘米。
答:三角形CDH的面积是7平方厘米。
【点睛】解答此题的主要依据是:等底等高的三角形的面积相等。
29.4厘米
【分析】根据题意可知,阴影部分面积比三角形ADH面积大8平方厘米,那么阴影部分面积加上梯形DBCH的面积比三角形ABC的面积大8平方厘米,已知三角形底是BC=8厘米,高AC=10厘米,根据三角形面积公式:底×高÷2,求出三角形ABC的面积,再加上8平方厘米就等于阴影部分面积与梯形面积DBCH的面积和,即平行四边形FBCE的面积,已知BC=8厘米,根据平行四边形面积公式:底×高,即可求出CH的长,再用AC的长减去CH的长,即可求出AH的长。
【详解】(8×10÷2+8)÷8
=(80÷2+8)÷8
=(40+8)÷8
=48÷8
=6(厘米)
10-6=4(厘米)
答:AH的长是4厘米。
【点睛】解答本题的关键是明确平行四边形面积与三角形ABC的关系,再利用三角形面积公式、平行四边形面积公式,进行解答。
30.64平方厘米
【分析】连接DB,(图如下)三角形ABC分成两个三角形ABD与三角形CDB;由此可知,三角形ABD的高与三角形CDB的高相等,等于正方形的边长,根据三角形面积公式:底×高÷2,求出正方形的边长,再根据正方形面积公式:边长×边长,求出正方形面积。
【详解】连接DB
设正方形边长为a
三角形ABC的面积:
40×10÷2
=400÷2
=200(平方厘米)
三角形ABD的面积:
40×a÷2
=20a(平方厘米)
三角形CDB的面积:
10×a÷2
=5a(平方厘米)
20a+5a=200
25a=200
a=200÷25
a=8(厘米)
正方形面积:
8×8=64(平方厘米)
答:正方形面积是64平方厘米。
【点睛】解答本题的关键是连接BD,再根据三角形面积在之间的关系,求出正方形的边长,再根据正方形面积公式,求出正方形面积。
31.18平方厘米
【分析】根据题意可知,BO=2DO,三角形DOC与三角形COB的高相等,三角形DOC的面积等于三角形COB面积的一半;已知三角形COB(阴影部分)面积是4平方厘米,三角形DOC的面积=4÷2=2平方厘米;三角形ADC与三角形BDC是等底等高,三角形ADC的面积等于三角形BDC的面积,三角形DOA的面积等于三角形COB (阴影部分)面积=4平方厘米;三角形ADO与三角形ABO是等高,且BO=2DO,三角形ABO的面积等于三角形ADO面积×2,即4×2=8平方厘米,把三角形COB的面积+三角形COD的面积+三角形AOD的面积+三角形ABO的面积,就是梯形ABCD的面积,即可解答。
【详解】BO=2DO
三角形DOC的面积:
4÷2=2(平方厘米)
三角形AOD面积=三角形COB的面积=4平方厘米
三角形ABO的面积=三角形AOD的面积×2
=4×2
=8(平方厘米)
梯形ABCD的面积:
4+2+4+8
=6+4+8
=10+8
=18(平方厘米)
【点睛】解答本题的关键明确等高的三角形中,三角形底边的比等于它们面积比,再根据阴影部分面积进行计算即可。
32.5厘米
【分析】“两块阴影部分的面积之和比三角形EFG的面积大10平方厘米”那么图中阴影部分面积加上中间梯形的面积(即这个平行四边形的面积)仍比三角形EFG的面积加上梯形的面积之和(即三角形BCE的面积)大10平方厘米,所以可得等量关系:平行四边形的面积=三角形BCE的面积+10平方厘米;据此解答.
【详解】8×10÷2=40(平方厘米)
40+10=50(平方厘米)
50÷10=5(厘米)
所以CF长为5厘米.
21世纪教育网(www.21cnjy.com)
组合图形和不规则图形的面积知识点梳理+题型总结
联系已学知识认识简单的组合图形,能把组合图形分解成已经学过的平面图形并计算出面积。
运用数方格法对不规则图形的面积进行估算,初步体会化难为易、化繁为简的解题策略和数学方法。
能用多种策略解决问题,激发探究数学问题的积极性。
1、组合图形的面积
在计算组合图形的面积时,通常先把组合图形分割成已学过的简单图形,分别计算出各个简单图形的面积,再把它们加起来,也可以把组合图形补成一个简单的图形,再用补成的简单图形的面积减去补上的简单图形的面积。
2、不规则图形的面积
求不规则图形的面积,可以用数方格法进行估计。估计时,先数整格的,再数不满整格的,不满整格的按半格计算。
重难点一:用分割和添补法解决简单组合图形的问题
【例题】 求下面各图形的面积。(单位:厘米)
梯形的高:
【变式1】求下列组合图形的面积.(单位:
【思路引导】这个组合图形的面积等于底为50分米,高为10分米的三角形面积加长50分米,宽40分米的长方形面积.根据三角形面积计算公式“”、长方形面积计算公式“”即可解答.
【完整解答】解:
答:这个组合图形的面积是.
故答案为:2250.
【变式2】华丰小学校园里有一块空地(如图).如果在这块空地上种草坪,每平方米草坪的价格是15元.需要多少钱?
【思路引导】如图,,这块空地的面积长方形的面积三角形的面积,长方形的长是,宽是;三角形的底是,高是,根据长方形和三角形的面积公式,求出这块地的面积,然后再根据乘法的意义,乘上15即可.
【完整解答】解:
(平方米)
(元
答:需要1755元钱.
【变式3】 如图,在四边形ABCD中,∠CBA和∠CDA都是直角,AD=10厘米,BC=6厘米,∠BAD=45°,求四边形ABCD的面积。
【完整解答】解:,
,
(平方厘米),
答:四边形的面积是20平方厘米.
重难点二:不规则图形面积的计算
【例题】下面是一个湖泊的平面图(每个小方格表示1公顷)。你能估计这个湖泊的面积大约是多少公顷吗?
①只数整格的,实际面积比数出的结果要大一些。
②把不满整格的也当作整格数,实际面积比数出的要小一些。
答案:整格的有55个,面积是55公顷。不满整格的有36个,面积大约是18公顷。
55+18=73(公顷)
答:这个湖泊的面积大约是73公顷。
分析:求不规则图形的面积,可以用数方格的方法进行估算。估算时,先数整格
的,再数不满整格的,不满整格的按半格计算,最后把两个结果相加,这样得到
的近似数最接近实际结果,比较合理。
【变式题】数一数,算一算。(每个小方格表示1平方厘米)
(1)如下图,一朵花所占的格子中,整格的有( )个,不满整格的有( )个,面积大约是( )平方厘米。
(2)如下图,一片树叶所占的格子中,整格的有( )个,不满整格的有( )个,面积大约是( )平方厘米。
答案:(1)6,16,14
(2)30,26,43
一、选择题
1.下图中树叶的面积大约是( )平方厘米。
A.26 B.56 C.39 D.22
2.如图,平行四边形的面积是18平方厘米,那么长方形的面积( )。
A.大于18平方厘米 B.等于18平方厘米
C.小于18平方厘米 D.无法比较
3.如图中阴影甲的面积比阴影乙的面积大( )。
A.6平方厘米 B.8平方厘米
C.4平方厘米 D.10平方厘米
二、填空题
4.下图平行四边形的面积是16平方厘米,涂色部分的面积是( )。
三、计算题
5.求下面图形的面积。
6.计算下面图形的面积。
7.计算下面图形中涂色部分的面积。(单位:厘米)
8.计算下面图形的面积。
9.计算下面图形涂色部分的面积。(单位:厘米)
(1)
(2)
10.如下图所示,求阴影部分的面积。(单位:米)
11.求彩色部分的面积(单位:厘米)。
12.如图,四边形ACDB和四边形DEFG都是正方形,已知厘米,厘米,求三角形BCF的面积。
13.计算下面图形阴影部分的面积。(单位:厘米)
14.求阴影部分面积。(单位:厘米)
四、解答题
15.如图,大正方形的边长是14厘米,小正方形的边长是10厘米。求阴影部分的面积。
16.如图,一块长方形草地,长方形的长是16米,宽是12米,中间铺了两条石子路(如图示意),那么草地部分面积有多少平方米?
17.一块近似平行四边形的草坪,被一条长方形的石子路分成了两块(如图)。已知平行四边形的底是39米,小路宽1米。这个草坪的面积是多少平方米?
18.王亮家要粉刷一面墙(如图,中间是窗户)。(单位:米)
(1)请你帮他算一算,要粉刷多大的面积?
(2)如果每平方米要用涂料2千克,一共要买多少千克涂料?
19.数学实践活动课中,李明把一张平行四边形的纸剪成一个三角形和一个梯形(如下图)。已知三角形的面积和梯形的面积相差18平方厘米,剪出的梯形面积是多少平方厘米?
20.如图所示,长方形的长和宽分别是8厘米和6厘米,阴影部分的总面积是16平方厘米。求四边形ABCD的面积。
21.已知一个四边形中∠B=∠D=90°,∠C=45°,AD=4cm,试求出这个四边形的面积是多少?(单位:厘米)
22.如下图所示,四边形ABCD周长为18cm,图中P点到四边形ABCD的距离相同为3cm,求四边形ABCD的面积。
23.在平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,求平行四边形ABCD面积。
24.如下图,一个长方形被一些直线分成若干个小块,已知三角形ADG的面积是11平方厘米,三角形BCH的面积是23平方厘米,求四边形EGFH的面积。
25.如图,已知三角形ABC中,DC=2BD,CE=4AE。阴影部分面积是20平方厘米,求三角形ABC的面积。
26.如图,四边形ABCD是边长为8厘米的正方形,梯形AEBD的两条对角线交于O,三角形AOE的面积比三角形BOD的面积小16平方厘米。求梯形AEBD的面积。
27.图中两个正方形的边长分别是10厘米和8厘米,求阴影部分的面积?
28.四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。三角形CDH的面积是多少平方厘米?
29.如图,平行四边形BCEF中,厘米,直角三角形中,厘米,阴影部分面积比三角形ADH的面积大8平方厘米。求AH长多少厘米?
30.在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)
31.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?
32.如图平行四边形ABCD的边BC长为10厘米,直角三角形BCE的直角边CE长为8厘米.已知两块阴影部分的面积之和比三角形EFG的面积大10平方厘米.CF长是多少厘米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】先数完整的格子数量,再数不足一格的数量,不足一格的按半格计算,最后求和即可。
【详解】整格有22个,半格有34个。
22+34÷2
=22+17
=39(平方厘米)
下图中树叶的面积大约是39平方厘米。
故答案为:C
【点睛】熟练掌握数格法求不规则图形的面积的方法是解答本题的关键。
2.B
【分析】把长方形沿对角线分成两个完全一样的三角形,每个三角形的底等于平行四边形的底,每个三角形的高等于平行四边形的高,因为等底等高的平行四边形的面积是三角形面积的2倍,所以这两个三角形(阴影部分)的面积等于平行四边形,也就是长方形的面积等于平行四边形的面积;据此解答即可。
【详解】因为等底等高的平行四边形的面积是三角形面积的2倍,所以这两个三角形(阴影部分)的面积等于平行四边形,也就是长方形的面积等于平行四边形的面积。
故答案为:B
【点睛】此题考查的目的是理解掌握等底等高的三角形与平行四边形面积之间的关系及应用,等底等高的平行四边形与长方形面积之间的关系及应用。
3.A
【分析】求阴影甲与阴影乙的面积差,实际上是求大三角形与正方形的面积差,将数据代入三角形和正方形的面积
【详解】(6+8)×6÷2-6×6
=14×6÷2-36
=42-36
=6(平方厘米)。
【点睛】本题的关键是将阴影部分的面积进行转化。
4.8平方厘米
【分析】根据观察图可知涂色部分是一个三角形,该三角形和平行四边形等底等高,所以涂色部分的面积是该四边形面积的一半,据此分析即可。
【详解】由分析可知,涂色部分的面积是平行四边形面积的一半,
所以涂色部分面积为:
16÷2=8(平方厘米)
【点睛】本题主要考查了等底等高的平行四边形和三角形的面积关系,即等底等高的三角形的面积是平行四边形的一半,要求学生熟练掌握并且会灵活运用。
5.143cm2
【分析】由图可知,图形的面积=三角形的面积+长方形的面积,根据三角形的面积=底×高÷2,长方形的面积=长×宽,代入数据进行解答即可。
【详解】(8+7)×(20-14)÷2
=15×6÷2
=90÷2
=45(cm2)
45+7×14
=45+98
=143(cm2)
图形的面积是143cm2。
6.84cm2;54m2;192cm2
【分析】(1)根据平行四边形的面积=底×高,代入数据计算即可求解。
(2)观察图形可知,组合图形的面积=三角形的面积+梯形的面积,根据三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算即可求解。
(3)如下图,补齐缺口处,那么组合图形的面积=梯形的面积-正方形的面积,根据梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,代入数据计算即可求解。
【详解】(1)8×10.5=84(cm2)
平行四边形的面积是84cm2。
(2)9×4÷2+(9+3)×6÷2
=36÷2+12×6÷2
=18+36
=54(m2)
组合图形的面积是54m2。
(3)(8+24)×(8+8)÷2-8×8
=32×16÷2-64
=256-64
=192(cm2)
组合图形的面积是192cm2。
7.42平方厘米;26平方厘米
【分析】(1)涂色部分的面积=平行四边形的面积-三角形的面积。根据平行四边形的面积=底×高,用8×6求出平行四边形的面积(48平方厘米);三角形的底是8-3-2=3(厘米),根据三角形的面积=底×高÷2,用3×4÷2求出三角形的面积(6平方厘米);用48-6求出涂色部分的面积。
(2)如下图,涂色部分的面积=正方形ABCD的面积+正方形CEFG的面积-三角形ABD的面积-三角形BEF的面积。根据正方形的面积=边长×边长,用8×8求出正方形ABCD的面积(64平方厘米),用6×6求出正方形CEFG的面积(36平方厘米);根据三角形的面积=底×高÷2,用8×8÷2求出三角形ABD的面积(32平方厘米),用(8+6)×6÷2求出三角形BEF的面积(42平方厘米);最后用64+36-32-42求出涂色部分的面积。
【详解】8×6-(8-3-2)×4÷2
=48-3×4÷2
=48-12÷2
=48-6
=42(平方厘米)
涂色部分面积是42平方厘米。
8×8+6×6-8×8÷2-(8+6)×6÷2
=64+36-32-14×6÷2
=100-32-84÷2
=68-42
=26(平方厘米)
涂色部分面积是26平方厘米。
8.1050cm2;42cm2
【分析】第一个图形是平行四边形,其中一条边是30cm,另在这条边上的高是35cm,根据平行四边形面积=底×高,计算得出面积;第二个图形是一个梯形和一个长方形组合起来的图形,根据梯形面积=(上底+下底)×高÷2,长方形面积=长×宽,两个面积相加得出答案。
【详解】第一个图形面积为:(cm2);
第二个图形面积为:
(cm2)
9.(1)36平方厘米
(2)33.75平方厘米
【分析】(1)观察图形可得:涂色部分的面积=底为12厘米、高为6厘米的平行四边形的面积-底为12厘米、高为6厘米的三角形的面积,然后再根据平行四边形的面积公式S=ah、三角形的面积公式S=ah÷2进行解答。
(2)观察图形可得:涂色部分的面积=长为5厘米、宽为2.5厘米的长方形的面积+上底为2.5厘米、下底为6厘米、高为(10-5)厘米的梯形的面积,然后再根据长方形的面积公式S=ab、梯形的面积公式S=(a+b)h÷2进行解答。
【详解】(1)12×6-12×6÷2
=72-36
=36(平方厘米)
涂色部分的面积是36平方厘米。
(2)5×2.5+(2.5+6)×(10-5)÷2
=12.5+8.5×5÷2
=12.5+21.25
=33.75(平方厘米)
涂色部分的面积是33.75平方厘米。
10.31.5平方米
【分析】由题意可以看出,阴影部分面积等于边长是9米的正方形面积的一半加上边长是6米的正方形面积,再减去底为(9+6)米,高为6米的三角形面积.根据正方形的面积计算公式“S=a2”及三角形面积计算公式“S=ab”即可求出阴影部分面积。
【详解】9×9×+6×6-×(9+6)×6
=81×+36-×15×6
=40.5+36-45
=76.5-45
=31.5(平方米)
阴影部分面积是31.5平方米。
11.13.5平方厘米
【分析】观察图形可知,彩色部分是一个三角形,三角形的底是(5+4)厘米,高是3厘米。三角形的面积=底×高÷2,据此代入数据计算。
【详解】(5+4)×3÷2
=9×3÷2
=13.5(平方厘米)
则彩色部分的面积是13.5平方厘米。
12.32平方厘米
【分析】观察图形可知,三角形BCF的面积等于正方形ACDB、正方形DEFG和三角形BGF的面积和减去三角形ACB和三角形CEF的面积,据此解题即可。
【详解】[8×8+6×6+6×(8-6)÷2]-[8×8÷2+(8+6)×6÷2]
=[8×8+6×6+6×2÷2]-[8×8÷2+14×6÷2]
=[64+36+6]-[32+42]
=106-74
=32(平方厘米)
三角形BCF的面积是32平方厘米。
13.33.75平方厘米;30平方厘米
【分析】由图可知,此图可以分割成如下图所示图形,阴影面积=长方形面积+三角形面积,根据长方形面积计算公式S=ab和三角形的面积公式S=ah÷2即可求解;
由图可知,阴影面积=大三角形面积-小三角形面积,利用三角形的面积公式S=ah÷2即可求解。
【详解】2.5×10+(6-2.5)×(10-5)÷2
=25+3.5×5÷2
=25+8.75
=33.75(平方厘米)
10×(10+6)÷2-10×10÷2
=10×16÷2-50
=80-50
=30(平方厘米)
14.64平方厘米;42平方厘米;50平方厘米
【详解】图1阴影部分的面积:
16×16-(16×16÷2+16×8÷2)
=256-(128+64)
=64(平方厘米)
图2阴影部分的面积:
10×10+8×8-10×10÷2-(10+8)×8÷2
=164-50-72
=42(平方厘米)
设图3小正方形的边长为a,则阴影部分的面积:
×10×10+×(a+10)×a-×(a+10)×a
=×10×10
=50(平方厘米)
15.98平方厘米。
【分析】
通过观察图形可知,如图:阴影部分的面积等于长(14+10)厘米,宽14厘米的长方形的面积减去空白部分3个三角形的面积(1号三角形的底和高都为14厘米;2号三角形的底为14+10=24厘米,高为10厘米;3号三角形的底为10厘米,高为14-10=4厘米),根据长方形的面积公式;S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】(14+10)×14-14×14÷2-(14+10)×10÷2-(14-10)×10÷2
=24×14-196÷2-24×10÷2-4×10÷2
=336-98-120-20
=238-120-20
=118-20
=98(平方厘米)
答:阴影部分的面积是98平方厘米。
16.140平方米
【分析】用平移的方法,把分割开的四块草地拼成一个新的长方形,这个新的长方形的长为(16-2)米、宽为(12-2)米,根据长方形的面积=长×宽,即可求出草地部分的面积。
【详解】(16-2)×(12-2)
=14×10
=140(平方米)
答:草地部分面积有140平方米。
17.912平方米
【分析】这个草坪的面积等于底为39米,高为24米的平行四边形的面积减去一个长为24米,宽为1米的长方形石子路的面积,分别利用平行四形和长方形的面积公式,代入数据即可求出这个草坪的面积。
【详解】39×24-1×24
=936-24
=912(平方米)
答:这个草坪的面积是912平方米。
【点睛】此题主要考查组合图形的面积的计算方法,熟练运用平行四形和长方形的面积公式解决问题。
18.(1)17平方米
(2)34千克
【分析】(1)根据墙的示意图,粉刷部分的面积是上面的三角形面积加下面的正方形面积减去长方形(窗)的面积;
(2)用每平方米用的涂料2千克乘粉刷面积就可以求出一共要买多少千克涂料,据此解答。
【详解】(1)(1+4+1)×1÷2+4×4-1×2
=3+16-2
=17(平方米)
答:要粉刷多大的面积是17平方米。
(2)2×17=34(千克)
答:一共要买34千克涂料。
【点睛】考查组合图形面积的计算及解决实际问题。
19.39平方厘米
【分析】根据平行四边形面积公式:面积=底×高;代入数据,求出平行四边形面积;三角形面积+梯形面积=平行四边形面积;三角形面积和梯形面积相差18平方厘米,即三角形面积+三角形面积+18=平行四边形面积,三角形面积=(平行四边形面积-18)÷2,据此求出三角形面积,进而求出梯形面积。
【详解】(10×6-18)÷2
=(60-18)÷2
=42÷2
=21(平方厘米)
21+18=39(平方厘米)
答:剪出的梯形面积是39平方厘米。
【点睛】利用平行四边形面积公式,根据三角形面积与梯形面积之间的关系,三角形、梯形和平行四边形面积之间的关系,进行解答。
20.4平方厘米
【分析】根据三角形的面积公式得出△AEF和△AGH的面积和正好等于长方形EFGH的面积的面积的一半,根据长方形的面积求出△ECH的面积,结合图形求出即可。
【详解】△AEF和△AGH的面积和正好等于长方形EFGH的面积的面积的一半,即
×8×6
=4×6
=24(平方厘米)
四边形EFGH是长方形,△ECH的面积是长方形面积的
×8×6
=2×6
=12(平方厘米)
所以,四边形ABCD的面积是:
12-(24 -16)
=12-8
=4(平方厘米)
答:四边形ABCD的面积是4平方厘米。
【点睛】本题考查了三角形的面积和正方形的面积的应用,主要考查学生能否根据图形把求不规则图形的面积转化成求规图形的面积。
21.42平方厘米
【分析】延长BA和CD,相较于一点于E,那么四边形的面积=三角形BCE的面积-三角形ADE的面积。
【详解】
如图所示,∠E=45°,所以三角形AED是等腰直角三角形,AD=DE=4cm,三角形BCE也是等腰直角三角形,BC=BE=10cm。所以四边形的面积为:
10×10÷2-4×4÷2
=50-8
=42(平方厘米)
【点睛】此题考查了组合图形的面积计算,运用了填补法。认真观察图形解答即可。
22.27平方厘米
【分析】根据题意,把P点与ABCD四个点连接,把四边形ABCD分成四个三角形,如图,三角形APB,三角形BPC,三角形CPD,三角形DPA,根据三角形面积公式:底×高÷2,三角形APB的面积=AB×3÷2;三角形BPC的面积=BC×3÷2;三角形CPD的面积=CD×3÷2;三角形DPA的面积=AD×3÷2,四个三角形相加,就是四边形ABCD的面积,即:AB×3÷2+BC×3÷2+CD×3÷2+DA×3÷2,再化为:(AB+BC+CD+DA)×3÷2,即四边形ABCD的周长×3÷2 代入数据,即可解答。
【详解】18×3÷2
=54÷2
=27(平方厘米)
答:四边形ABCD的面积是27平方厘米。
【点睛】解答本题的关键是把四边形平成四个高是3厘米的三角形,再利用三角形面积公式,求出四边形的面积。
23.54平方厘米
【分析】根据题意可知,AE=EF=EB,由此可知三角形AEG=三角形EFG=三角形FBG,三角形ABG的面积=6×3=18平方厘米;AG=2CG,由此可知三角形CBG的面积=三角形ABG面积÷2,即三角形CBG的面积=18÷2=9平方厘米,三角形ABC的面积=三角形ABG的面积+CBG的面积=18+9=27平方厘米,平行四边形ABCD的面积=三角形ABC的面积×2,用27×2,即可解答。
【详解】三角形ABG的面积:
6×3=18(平方厘米)
三角形CBG的面积:
18÷2=9(平方厘米)
三角形ABC的面积:
18+9=27(平方厘米)
平行四边形ABCD的面积:
27×2=54(平方厘米)
答:平行四边形ABCD的面积是54平方厘米。
【点睛】解答本题的关键是利用三角形等底等高,求出三角形面积,再利用三角形面积求出平行四边形面积。
24.34平方厘米
【分析】由题意可知:S△ADE+S△ECB=S△DCF,等式的两边分别去掉公共部分,即S△DGE+S△EHC,则剩余的部分的面积仍然相等,即S△ADG +S△ADG =S四边形EGFH,据此代入数据即可求解。
【详解】因为S△ADE+S△ECB=S△DCF
等式的两边分别去掉公共部分,即S△DGE+S△EHC
即S△ADG +S△BCH =S四边形EGFH
11+23=34(平方厘米)
答:求四边形EGFH的面积是34平方厘米。
【点睛】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半。
25.150平方厘米
【分析】如果两个三角形的高相等,那么这两个三角形的面积比等于它们底的比,先求出三角形DCE的面积,再求三角形ABD的面积然后加上阴影部分面积即可求大三角形的面积。
【详解】由题意可知:三角形DCE面积=三角形ADE面积×4
20×4=80(平方厘米)
三角形ADB面积:
三角形ADC面积×
=(三角形ADE面积+三角形DCE面积)×
=(20+80)×
=100×
=50(平方厘米)
三角形ABC面积=50+80+20=150(平方厘米)
答:三角形ABC的面积是150平方厘米。
【点睛】此题关键是利用“如果两个三角形的高相等,那么这两个三角形的面积比等于它们底的比”求解。
26.48平方厘米
【分析】在梯形AEBD中,三角形ABD和三角形EBD是同底等高,所以三角形ABD面积=三角形EBD面积,进而求出三角形AOD面积=三角形EBO的面积;因为三角形BOD面积比三角形AOE的面积大16平方厘米,因此三角形BOD面积+三角形AOD的面积(即三角形ABD的面积)-(三角形EBO的面积+三角形AOE的面积)=16,由于三角形ABD的面积=正方形ABCD面积的一半,所以三角形EBO的面积+三角形AOE的面积=三角形ABD的面积-16平方厘米,根据三角形面积公式:底×高÷2,三角形ABD的面积=8×8÷2=32;三角形EBO的面积+三角形AOE的面积=32-16=16,梯形AEBD的面积=三角形EOB的面积+三角形AOE的面积+三角形ABD的面积,即32+16=48平方厘米,据此解答。
【详解】三角形AOE的面积+三角形EBO的面积:
8×8÷1-16
=64÷2-16
=32-16
=16(平方厘米)
梯形面积:
32+16=48(平方厘米)
答:梯形AEBD的面积是48平方厘米。
【点睛】解答本题关键明确等底等高的三角形面积相等,利用等量代换的方法进行解答。
27.50平方厘米
【分析】如图,要求阴影部分的面积,可以先求三角形BCD和梯形CEFD的面积,然后减去下面三角形BEF的面积,据此解答。
【详解】S△BCD+S梯形CEFD-S△BEF=阴影面积
10×10÷2+(8+10)×8÷2-8×(10+8)÷2
=50+72-72
=50(平方厘米)
答:阴影部分的面积是50平方厘米。
【点睛】此题主要考查学生利用灵活转化的思想球图形面积的能力。
28.7平方厘米
【分析】如下图所示,连接FD,则三角形FDC和三角形AFD等底等高,则二者的面积相等,分别减去公共部分三角形FHD,则剩余部分的面积仍然相等,即三角形AFH和三角形CDH的面积相等,据此即可得解。
【详解】连接FD,则三角形FDC和三角形AFD等底等高,则二者的面积相等,分别减去公共部分三角形FHD,则剩余部分的面积仍然相等;
即三角形AFH和三角形CDH的面积相等,所以三角形CDH的面积也等于7平方厘米。
答:三角形CDH的面积是7平方厘米。
【点睛】解答此题的主要依据是:等底等高的三角形的面积相等。
29.4厘米
【分析】根据题意可知,阴影部分面积比三角形ADH面积大8平方厘米,那么阴影部分面积加上梯形DBCH的面积比三角形ABC的面积大8平方厘米,已知三角形底是BC=8厘米,高AC=10厘米,根据三角形面积公式:底×高÷2,求出三角形ABC的面积,再加上8平方厘米就等于阴影部分面积与梯形面积DBCH的面积和,即平行四边形FBCE的面积,已知BC=8厘米,根据平行四边形面积公式:底×高,即可求出CH的长,再用AC的长减去CH的长,即可求出AH的长。
【详解】(8×10÷2+8)÷8
=(80÷2+8)÷8
=(40+8)÷8
=48÷8
=6(厘米)
10-6=4(厘米)
答:AH的长是4厘米。
【点睛】解答本题的关键是明确平行四边形面积与三角形ABC的关系,再利用三角形面积公式、平行四边形面积公式,进行解答。
30.64平方厘米
【分析】连接DB,(图如下)三角形ABC分成两个三角形ABD与三角形CDB;由此可知,三角形ABD的高与三角形CDB的高相等,等于正方形的边长,根据三角形面积公式:底×高÷2,求出正方形的边长,再根据正方形面积公式:边长×边长,求出正方形面积。
【详解】连接DB
设正方形边长为a
三角形ABC的面积:
40×10÷2
=400÷2
=200(平方厘米)
三角形ABD的面积:
40×a÷2
=20a(平方厘米)
三角形CDB的面积:
10×a÷2
=5a(平方厘米)
20a+5a=200
25a=200
a=200÷25
a=8(厘米)
正方形面积:
8×8=64(平方厘米)
答:正方形面积是64平方厘米。
【点睛】解答本题的关键是连接BD,再根据三角形面积在之间的关系,求出正方形的边长,再根据正方形面积公式,求出正方形面积。
31.18平方厘米
【分析】根据题意可知,BO=2DO,三角形DOC与三角形COB的高相等,三角形DOC的面积等于三角形COB面积的一半;已知三角形COB(阴影部分)面积是4平方厘米,三角形DOC的面积=4÷2=2平方厘米;三角形ADC与三角形BDC是等底等高,三角形ADC的面积等于三角形BDC的面积,三角形DOA的面积等于三角形COB (阴影部分)面积=4平方厘米;三角形ADO与三角形ABO是等高,且BO=2DO,三角形ABO的面积等于三角形ADO面积×2,即4×2=8平方厘米,把三角形COB的面积+三角形COD的面积+三角形AOD的面积+三角形ABO的面积,就是梯形ABCD的面积,即可解答。
【详解】BO=2DO
三角形DOC的面积:
4÷2=2(平方厘米)
三角形AOD面积=三角形COB的面积=4平方厘米
三角形ABO的面积=三角形AOD的面积×2
=4×2
=8(平方厘米)
梯形ABCD的面积:
4+2+4+8
=6+4+8
=10+8
=18(平方厘米)
【点睛】解答本题的关键明确等高的三角形中,三角形底边的比等于它们面积比,再根据阴影部分面积进行计算即可。
32.5厘米
【分析】“两块阴影部分的面积之和比三角形EFG的面积大10平方厘米”那么图中阴影部分面积加上中间梯形的面积(即这个平行四边形的面积)仍比三角形EFG的面积加上梯形的面积之和(即三角形BCE的面积)大10平方厘米,所以可得等量关系:平行四边形的面积=三角形BCE的面积+10平方厘米;据此解答.
【详解】8×10÷2=40(平方厘米)
40+10=50(平方厘米)
50÷10=5(厘米)
所以CF长为5厘米.
21世纪教育网(www.21cnjy.com)
