江苏省海安县08-09学年高二上学期期末调研(数学理)
文档属性
| 名称 | 江苏省海安县08-09学年高二上学期期末调研(数学理) |

|
|
| 格式 | rar | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-11 00:00:00 | ||
图片预览


文档简介
江苏省海安县08-09学年高二上学期期末调研
(数学理科)试卷
(满分160分,考试时间120分钟)
一、填空题 本大题共14小题,每小题5分,共70分. 把答案填写在答题卡相应位置.
1. 三鹿婴幼儿奶粉事件发生后,质检总局紧急开展液态奶三聚氰胺的专项检查. 设?蒙牛、
?伊利、光明三家公司生产的某批次液态奶分别是2400箱、3600箱和4000箱,?现从中
?共抽取500箱进行检验,则这三家公司生产的液态奶被抽取的箱数依次为 ▲ .
2. 命题“=0”的否定是 ▲ .
3. 双曲线的离心率是 ▲ .
4. 将容量为100的样本数据分为8个组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
14
15
13
12
9
则第3组的频率为 ▲ .
5. 在平面直角坐标系xOy中,“ab>0”是“方程的曲线为椭圆”的 ▲ 条
?件(填写“充分不必要”、“必要不充分”、“充分必要”和“既不充分也不必要”之一).
6. 样本a1, a2, a3, …, a10的平均数为,样本b1, b2, b3, …, b20的平均数为, 则
?样本a1,a2,a3,…,a10, b1,b2,b3,…,b20的平均数为 ▲ (用,表示).
7. 根据如图所示的伪代码表示的算法,可得f(1)+f(4)= ▲ .
8. 从装有5只红球、5只白球的袋中任意取出3只球,有下
列事件:21世纪教育网
①“取出2只红球和1只白球”与“取出1只红球和2只白球”;
②“取出2只红球和1只白球”与“取出3只红球”; 21世纪教育网
③“取出3只红球”与“取出3只球中至少有1只白球”;
④“取出3只红球”与“取出3只白球”.
其中是对立事件的是 ▲ (写序号).
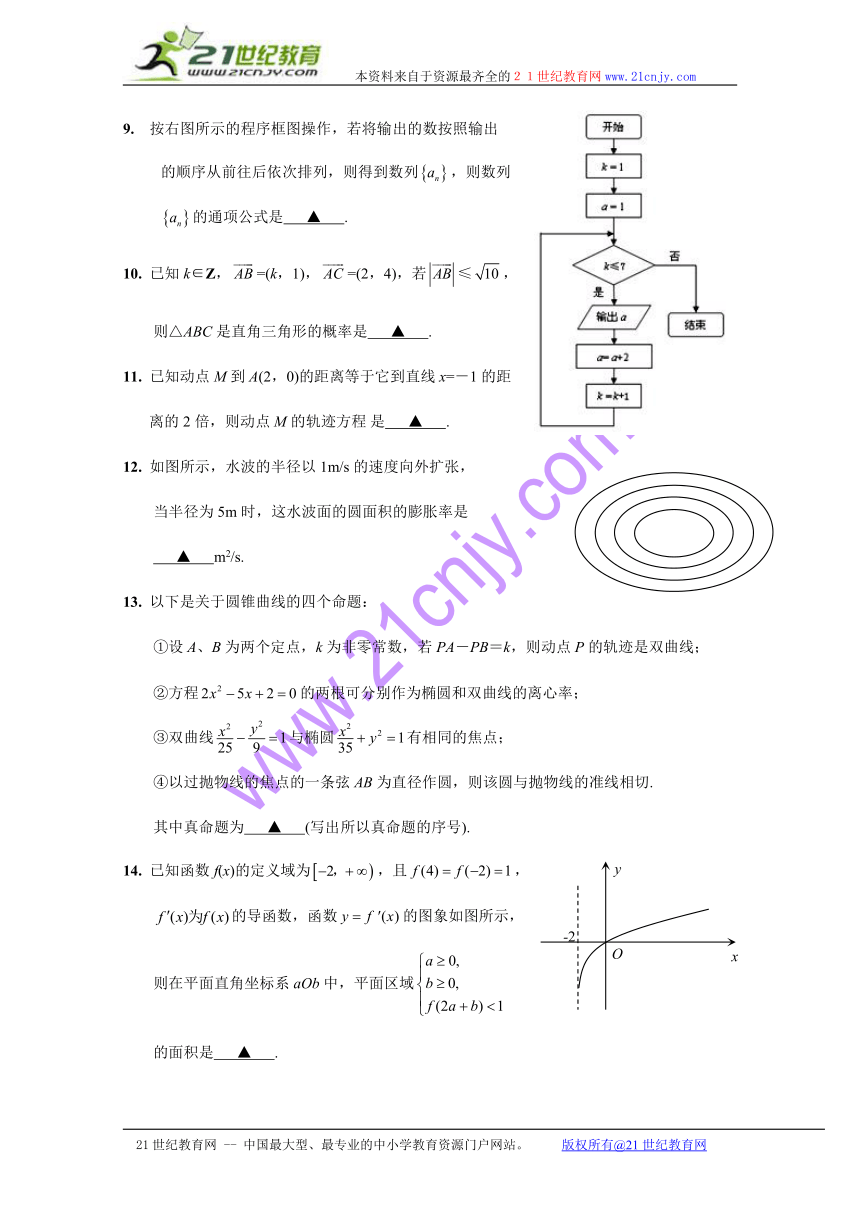
9. 按右图所示的程序框图操作,若将输出的数按照输出
?的顺序从前往后依次排列,则得到数列,则数列
?的通项公式是 ▲ .
10. 已知k∈Z,=(k,1),=(2,4),若≤,
则△ABC是直角三角形的概率是 ▲ . 21世纪教育网
11. 已知动点M到A(2,0)的距离等于它到直线x=-1的距
?离的2倍,则动点M的轨迹方程?是 ▲ .
12. 如图所示,水波的半径以1m/s的速度向外扩张,
当半径为5m时,这水波面的圆面积的膨胀率是
▲ m2/s.
13. 以下是关于圆锥曲线的四个命题:
①设A、B为两个定点,k为非零常数,若PA-PB=k,则动点P的轨迹是双曲线;
②方程的两根可分别作为椭圆和双曲线的离心率;
③双曲线与椭圆有相同的焦点;21世纪教育网
④以过抛物线的焦点的一条弦AB为直径作圆,则该圆与抛物线的准线相切.
其中真命题为 ▲ (写出所以真命题的序号).
14. 已知函数f(x)的定义域为,且,
的导函数,函数的图象如图所示,
则在平面直角坐标系aOb中,平面区域
的面积是 ▲ .
二、解答题:本大题共6小题,共90分. 请将解答填写在答题卡规定的区域内,否则答题无效. 解答应写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
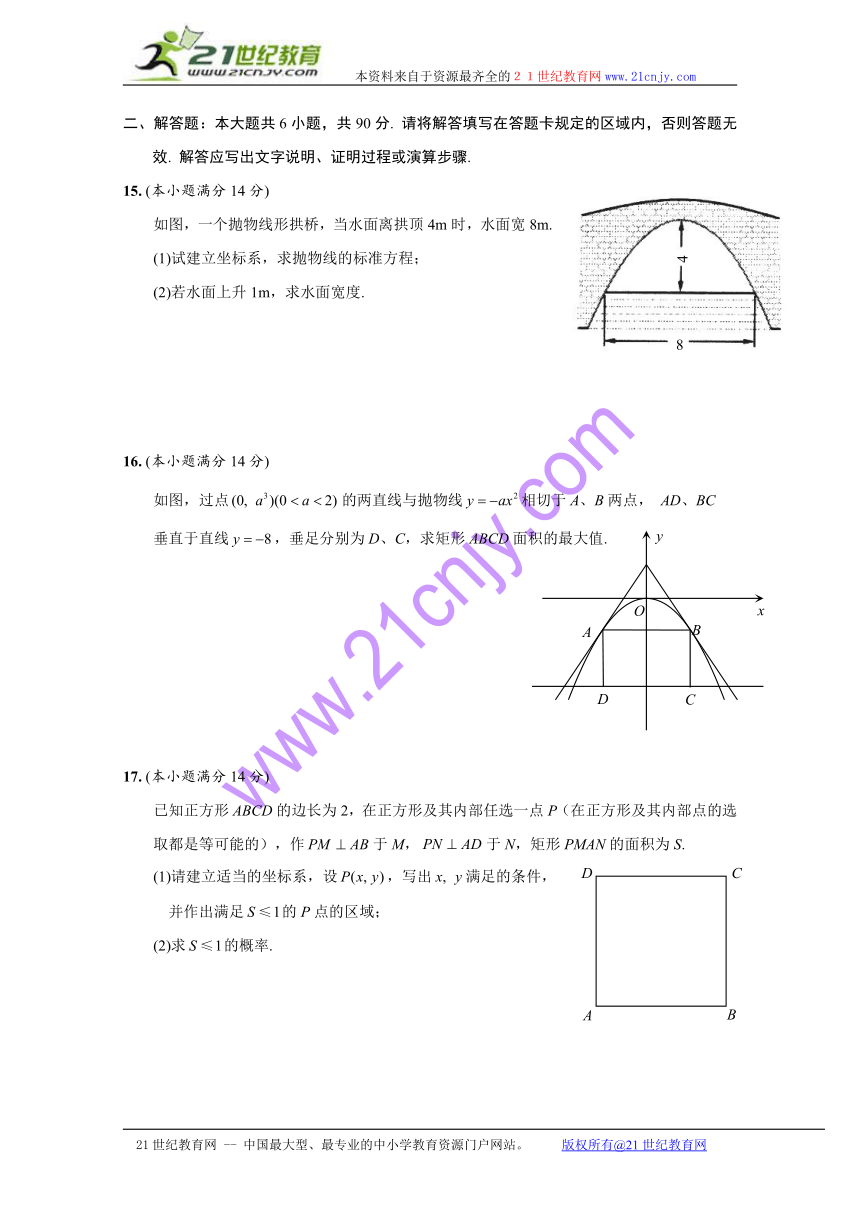
如图,一个抛物线形拱桥,当水面离拱顶4m时,水面宽8m.
(1)试建立坐标系,求抛物线的标准方程;
(2)若水面上升1m,求水面宽度. 21世纪教育网
16. (本小题满分14分)
如图,过点的两直线与抛物线相切于A、B两点, AD、BC
垂直于直线,垂足分别为D、C,求矩形ABCD面积的最大值.
17. (本小题满分14分)
已知正方形ABCD的边长为2,在正方形及其内部任选一点P(在正方形及其内部点的选取都是等可能的),作于M,于N,矩形PMAN的面积为S.
(1)请建立适当的坐标系,设,写出满足的条件,
并作出满足的P点的区域;
(2)求的概率.
18. (本小题满分16分)
如图所示,多面体ABCDS中,四边形ABCD为矩形,SD⊥AD,SD⊥AB,且=2,
,M、N分别为AB、CD中点.
(1)求证:SM⊥AN;
(2)求二面角A—SC—D的余弦值;
19. (本小题满分16分)
(1)证明:函数f ( x ) =在上是单调增函数;
(2)证明:. 21世纪教育网
20. (本小题满分16分)
如图,A为椭圆上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,AF1=3AF2.
(1) 求椭圆的离心率;
(2) 设,证明:当A点在椭圆上运动时,是定值.
高二(理科)数学参考答案及评分标准200901
填空题(5分×14=70分)
1. 120,180,200 2. 3. 2
4. 0.14 5. 必要不充分 6.
7. 1 ?8. ③ ?9.
10. 11. 12.
13. ②③④ 14. 4
二、解答题
15. (14分) 21世纪教育网
(1)如图建立坐标系,设抛物线的标准方程为. ------------------3分
由已知条件可知,点B的坐标是,代入方程,
得,即. -----------------------6分
所以,所求抛物线标准方程是 -----------------------7分
(2)若水面上升1m,则, ?-----------------------10分
代入,得,. ------------------13分
所以这时水面宽为m. -----------------------14分
16.(14分) 21世纪教育网
设切点为,则, -----------------------1分
因为,所以切线方程为, 即,----------3分
因为切线过点,所以,即,于是.--------------5分
将代入得. ------------------7分
(若设切线方程为,代入抛物线方程后由得到切点坐标,亦予认可.)
所以, ---------------------8分
所以矩形面积为, ----------------------9分
于是. -----------------------10分
所以当时,;当时,; ----------------------12分
故当时,S有最大值为. -----------------------14分
17.(14分)
(1)以直线AB为x轴,AD为y轴,A为坐标原点建立直角坐标系. ---------------------1分
因为点在正方形及其内部,
所以S=xy. -----------------------3分
故满足满足的点满足的条件是 --------5分
P点的区域如图. -----------------------7分
(2) P点所在的区域面积,---------------------12分
而正方形ABCD的面积为4,
所以的概率为. ------------------14分
18. (16分)
(1)建立如图所示的空间直角坐标系,则
A(0, 1, 0), N(0, 0, 1), S(, 0, 0), M(0, 1, 1), C(0, 0, 2),
-----------------------3分
, ,-----------------------6分
于是,
` 所以SM⊥SM. -----------------------8分
(2)设平面ASC的法向量为,
,,
则且,21世纪教育网
令,则. . -------------------12分
又平面SDC的一个法向量. -----------------------13分
设二面角A-SC-D的平面角为,则,
所以二面角A-SC-D的余弦值为. -----------------------16分
19.(1)对于函数,.------------2分
当时,; -----------------------4分
当时,. -------------------6分
故当时,总有. -----------------------7分
所以函数在区间上是单调增函数. -------------------8分
(2)由(1)知,, ---------------------10分
而. ----------------------11分
. --------------------14分
于是,即. -------------------16分
20.(1)设,则.
由题设及椭圆定义得 ---------------------2分
消去m得,所以离心率. -----------------------4分
(2)由(1)知:,所以椭圆方程可化为. ----------------------6分
设,,则.
若A为椭圆的长轴端点,则或,21世纪教育网
所以. ------------------7分
若A为椭圆上异于长轴端点的任意一点,则由得
,所以. -----------------8分
又直线的方程为, -----------------------9分
所以由得. -------------10分
因为,
所以, ---------------------12分
由韦达定理得,所以, --------------------13分
由对称性得. ----------------------14分
所以. ---------------15分
综上证得,当A点在椭圆上运动时,为定值6. ----------------------16分
(数学理科)试卷
(满分160分,考试时间120分钟)
一、填空题 本大题共14小题,每小题5分,共70分. 把答案填写在答题卡相应位置.
1. 三鹿婴幼儿奶粉事件发生后,质检总局紧急开展液态奶三聚氰胺的专项检查. 设?蒙牛、
?伊利、光明三家公司生产的某批次液态奶分别是2400箱、3600箱和4000箱,?现从中
?共抽取500箱进行检验,则这三家公司生产的液态奶被抽取的箱数依次为 ▲ .
2. 命题“=0”的否定是 ▲ .
3. 双曲线的离心率是 ▲ .
4. 将容量为100的样本数据分为8个组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
14
15
13
12
9
则第3组的频率为 ▲ .
5. 在平面直角坐标系xOy中,“ab>0”是“方程的曲线为椭圆”的 ▲ 条
?件(填写“充分不必要”、“必要不充分”、“充分必要”和“既不充分也不必要”之一).
6. 样本a1, a2, a3, …, a10的平均数为,样本b1, b2, b3, …, b20的平均数为, 则
?样本a1,a2,a3,…,a10, b1,b2,b3,…,b20的平均数为 ▲ (用,表示).
7. 根据如图所示的伪代码表示的算法,可得f(1)+f(4)= ▲ .
8. 从装有5只红球、5只白球的袋中任意取出3只球,有下
列事件:21世纪教育网
①“取出2只红球和1只白球”与“取出1只红球和2只白球”;
②“取出2只红球和1只白球”与“取出3只红球”; 21世纪教育网
③“取出3只红球”与“取出3只球中至少有1只白球”;
④“取出3只红球”与“取出3只白球”.
其中是对立事件的是 ▲ (写序号).
9. 按右图所示的程序框图操作,若将输出的数按照输出
?的顺序从前往后依次排列,则得到数列,则数列
?的通项公式是 ▲ .
10. 已知k∈Z,=(k,1),=(2,4),若≤,
则△ABC是直角三角形的概率是 ▲ . 21世纪教育网
11. 已知动点M到A(2,0)的距离等于它到直线x=-1的距
?离的2倍,则动点M的轨迹方程?是 ▲ .
12. 如图所示,水波的半径以1m/s的速度向外扩张,
当半径为5m时,这水波面的圆面积的膨胀率是
▲ m2/s.
13. 以下是关于圆锥曲线的四个命题:
①设A、B为两个定点,k为非零常数,若PA-PB=k,则动点P的轨迹是双曲线;
②方程的两根可分别作为椭圆和双曲线的离心率;
③双曲线与椭圆有相同的焦点;21世纪教育网
④以过抛物线的焦点的一条弦AB为直径作圆,则该圆与抛物线的准线相切.
其中真命题为 ▲ (写出所以真命题的序号).
14. 已知函数f(x)的定义域为,且,
的导函数,函数的图象如图所示,
则在平面直角坐标系aOb中,平面区域
的面积是 ▲ .
二、解答题:本大题共6小题,共90分. 请将解答填写在答题卡规定的区域内,否则答题无效. 解答应写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
如图,一个抛物线形拱桥,当水面离拱顶4m时,水面宽8m.
(1)试建立坐标系,求抛物线的标准方程;
(2)若水面上升1m,求水面宽度. 21世纪教育网
16. (本小题满分14分)
如图,过点的两直线与抛物线相切于A、B两点, AD、BC
垂直于直线,垂足分别为D、C,求矩形ABCD面积的最大值.
17. (本小题满分14分)
已知正方形ABCD的边长为2,在正方形及其内部任选一点P(在正方形及其内部点的选取都是等可能的),作于M,于N,矩形PMAN的面积为S.
(1)请建立适当的坐标系,设,写出满足的条件,
并作出满足的P点的区域;
(2)求的概率.
18. (本小题满分16分)
如图所示,多面体ABCDS中,四边形ABCD为矩形,SD⊥AD,SD⊥AB,且=2,
,M、N分别为AB、CD中点.
(1)求证:SM⊥AN;
(2)求二面角A—SC—D的余弦值;
19. (本小题满分16分)
(1)证明:函数f ( x ) =在上是单调增函数;
(2)证明:. 21世纪教育网
20. (本小题满分16分)
如图,A为椭圆上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,AF1=3AF2.
(1) 求椭圆的离心率;
(2) 设,证明:当A点在椭圆上运动时,是定值.
高二(理科)数学参考答案及评分标准200901
填空题(5分×14=70分)
1. 120,180,200 2. 3. 2
4. 0.14 5. 必要不充分 6.
7. 1 ?8. ③ ?9.
10. 11. 12.
13. ②③④ 14. 4
二、解答题
15. (14分) 21世纪教育网
(1)如图建立坐标系,设抛物线的标准方程为. ------------------3分
由已知条件可知,点B的坐标是,代入方程,
得,即. -----------------------6分
所以,所求抛物线标准方程是 -----------------------7分
(2)若水面上升1m,则, ?-----------------------10分
代入,得,. ------------------13分
所以这时水面宽为m. -----------------------14分
16.(14分) 21世纪教育网
设切点为,则, -----------------------1分
因为,所以切线方程为, 即,----------3分
因为切线过点,所以,即,于是.--------------5分
将代入得. ------------------7分
(若设切线方程为,代入抛物线方程后由得到切点坐标,亦予认可.)
所以, ---------------------8分
所以矩形面积为, ----------------------9分
于是. -----------------------10分
所以当时,;当时,; ----------------------12分
故当时,S有最大值为. -----------------------14分
17.(14分)
(1)以直线AB为x轴,AD为y轴,A为坐标原点建立直角坐标系. ---------------------1分
因为点在正方形及其内部,
所以S=xy. -----------------------3分
故满足满足的点满足的条件是 --------5分
P点的区域如图. -----------------------7分
(2) P点所在的区域面积,---------------------12分
而正方形ABCD的面积为4,
所以的概率为. ------------------14分
18. (16分)
(1)建立如图所示的空间直角坐标系,则
A(0, 1, 0), N(0, 0, 1), S(, 0, 0), M(0, 1, 1), C(0, 0, 2),
-----------------------3分
, ,-----------------------6分
于是,
` 所以SM⊥SM. -----------------------8分
(2)设平面ASC的法向量为,
,,
则且,21世纪教育网
令,则. . -------------------12分
又平面SDC的一个法向量. -----------------------13分
设二面角A-SC-D的平面角为,则,
所以二面角A-SC-D的余弦值为. -----------------------16分
19.(1)对于函数,.------------2分
当时,; -----------------------4分
当时,. -------------------6分
故当时,总有. -----------------------7分
所以函数在区间上是单调增函数. -------------------8分
(2)由(1)知,, ---------------------10分
而. ----------------------11分
. --------------------14分
于是,即. -------------------16分
20.(1)设,则.
由题设及椭圆定义得 ---------------------2分
消去m得,所以离心率. -----------------------4分
(2)由(1)知:,所以椭圆方程可化为. ----------------------6分
设,,则.
若A为椭圆的长轴端点,则或,21世纪教育网
所以. ------------------7分
若A为椭圆上异于长轴端点的任意一点,则由得
,所以. -----------------8分
又直线的方程为, -----------------------9分
所以由得. -------------10分
因为,
所以, ---------------------12分
由韦达定理得,所以, --------------------13分
由对称性得. ----------------------14分
所以. ---------------15分
综上证得,当A点在椭圆上运动时,为定值6. ----------------------16分
同课章节目录
