3.34函数的应用 课件(共17张PPT)-高中数学人教B版(2019)必修第一册
文档属性
| 名称 | 3.34函数的应用 课件(共17张PPT)-高中数学人教B版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 690.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
3.4函数的应用(一)
例1 设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额
与3.1.2例8相同,全年综合所得收入额为(单位:元),应缴纳综合所得个
(1)求y 关于的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全
年应缴纳多少综合所得个税
税税额为 y(单位:元).
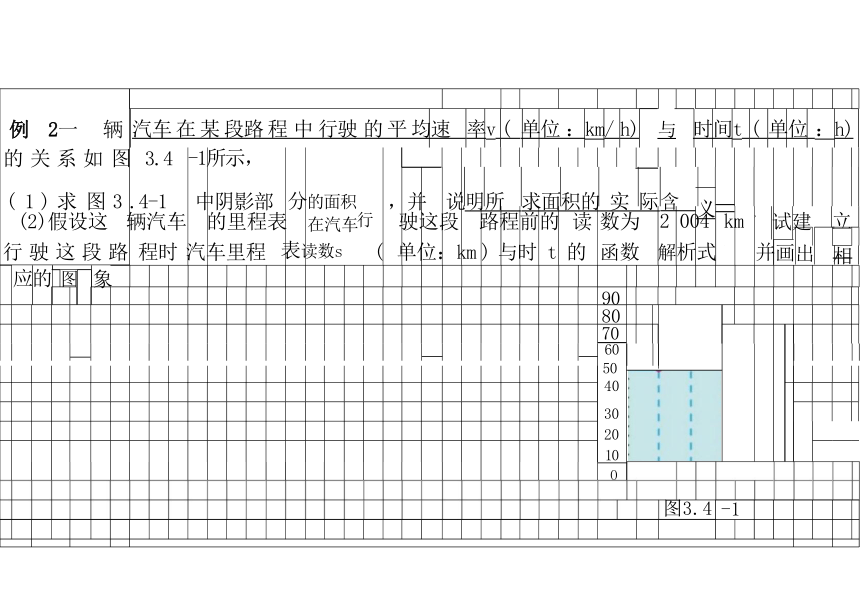
例 2一 辆 汽车 在 某 段路 程 中 行驶 的 平 均速 率v ( 单位 :km/ h) 与 时间t ( 单位 :h)
的 关 系 如 图 3.4 -1所示,
60
50
( 1 ) 求 图 3 .4-1 中阴影部 分的面积行 ,并 说明所 求面积的 实 际 含 义
(2)假设这 辆汽车 的里程表 在汽车 驶这段 路程前的 读 数为 2 004 km 试建 立
,
行 驶 这 段 路 程时 汽车里程 表读数s ( 单位:km ) 与时 t 的 函数 解析式 并画出 相
应的 图 象
,
90 80 70
40
30 20 10 O
图3.4 -1
[微 练 习 ]
市 场 营 销 人 员 的 个 人 月 收 入 与 其 每月 的销 量 成 一 次 函 数 关
1. 某 公 司
如 图 所 示 , 由 图 中 给 出 的 信 息 可 知 , 营销人 y 员没有销售量时的收 个收入/元 入 是 ( )
1300 x
800
l 2销售量/万件
0
A. 3 10 元 B. 3 00 元 C . 39 0 元 D. 2 80 元
B [ 由 图象 知 , , 当 该 =0 次 函 , 数 y 过 = ( 30 , 0.] 80 0) , (2 , 3 0 0) , 可 求 得 解 析 式 y =
50 0x + 30 0(x ≥ 0) x 时
系,
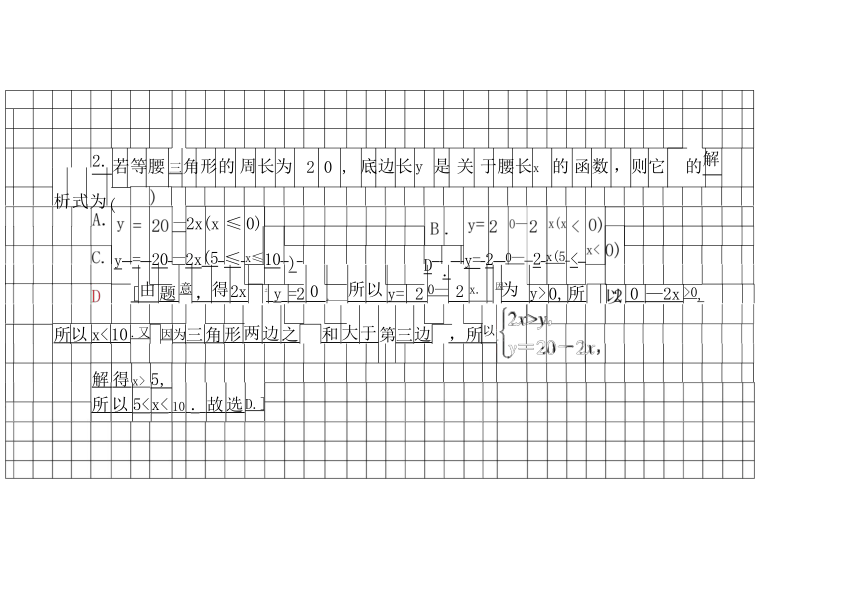
2. 若等腰 三角形的 周长为 2 0 , 底边长 y 是 关 于腰长x 的 函数 ,则它 的解
析式为(
—2x(x ≤ 0)
y = 20 —2x(5 ≤ x≤10 ) D . y= 2 0— 2 x(5 <
[由 题 意 ,得 2x y =2 0 , 所 以 y= 2 0— 2 x. 为 y> 0, 所 0 —2x >0,
所以 x< 10 .又 因为三 角 形 两 边 之 和 大 于 第三 边 ,所以
解 得 x> 5, 所 以 5< x< 10 . 故 选 D.]
因
+
A、B两地每台电脑的运费分别是40元、30元,乙地运往 A、B两地每台电脑
的运费分别是80元、50元.设甲地调运x 台电脑至B 地,该公司运往A 、B
两地的总运费为y 元 .
(1)求y 关于x 的函数关系式;
(2)若总运费不超过1000元,问有几种调运方案
(3)哪种方案总运费最低 并求出最低运费
探究点一 一次函数模型
[ 例 1] 某电脑公司在甲、乙两地各有一个分公司,甲地分公司现有电脑
6台,乙地分公司有同一型号的电脑12台.现A 地某单位向该公司购买该型
号的电脑10台,B 地某单位向该公司购买该型号的电脑8台. 已知甲地运往
地应 [解 调 ] 运( ( 8— ) x 甲 )台 地 电 调 运 x 至 台 B 电 地 脑 , 到 运 B 地 A , 地 则 剩 (8 下( — 6 x) —x ) 台 电 4) 运 脑 脑 台 到 ( A O≤ 地 , 乙
12—
脑 往 = (x + x ≤ 6,
x ∈ N) .
运
费 y = 30 x + 40 × (6 x ) + 50 × (8 x )+ 80 ×( x + 4) = 2 0x 十
9 60 (x ∈ N , 且 0 ≤x ≤ 6)
.
(2) 令 y ≤10 00 , 即 2 0x + 96 0 ≤ 0 00 , 得 x ≤ 2.
0≤ x ≤ 6, N
又 x∈ ,
∴0 ≤ x ≤2 , x ∈ N.
2 , 即 有 3 种 调 运 方 案
∴ x = 0 , , .
(3) ∵y 0≤ = x 2 0x + 96 0 N, 是 R 上 的 增 函 数 ,
又 ≤ 6, x ∈
∴当 x= 0 时 , y 有 最 小 值 9 6 0.
∴ 从 甲 地 运 6 台 到 A 地 , 从 乙 地 运 8 台 到 B 地 、 运 4 台到 A 地 , 此 时 运
费最 低 , 最 低 为 96 0
元 .
调
电
次 函 数 模 型 的 特 点 和 求 解 方 法
一
( ) 一 次 函 数 模 型 的 突 出 特 点 是 其 图象 是 一 条 直 线 .
(2 ) 解 一 次 函 数 模 型 时 , 注 意 待 定 系 数 法 的 应 用 , 主 要 步 骤 是 : 设 元 、 列
式 、 求 解 .
探究点二 二次函数模型
[例2] 某水果批发商销售进价为每箱40元的苹果,假设每箱售价不低于
50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每 天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元)之间的函数关系式;
(2)求该批发商平均每天的销售利润 w (元)与销售单价x(元)之间的函数关
系式;
(3)当每箱苹果的售价为多少元时,每天可以获得最大利润 最大利润是
多少
[ 解](1)根据题意,得y=90-3 (x—50),
化简得y=—3x+240(50≤x≤55,x∈N).
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利
润,所以w= (一3x+240)(x—40)=—3x +360x—9600(50≤x≤55,x∈N).
(3)因为w=—3x +360x—9600=-3(x—60) +1200,
所以当x<60 时 ,w 随 x 的增大而增大. 又50≤x≤55,x∈N,
所以当x=55 时 ,w 有最大值,最大值为1125.
所以当每箱苹果的售价为55元时,每天可以获得最大利润,最大利润是
1 1 2 5 元
二次函数模型的应用
根据实际问题建立二次函数模型后,可利用配方法、判别式法、换元法以
及函数的单调性等方法求最值,从而解决实际问题中的利润最大、用料最省等 最值问题.
[提醒] 利用二次函数求最值时,应特别注意取得最值时的自变量的值与
实际意义是否相符.
[例3] 国庆期间,某旅行社组团去风景区旅游,若旅行团人数为30人或
少于30人,则每人需交费用900元;若旅行团人数多于30人,则给予优惠: 每多1人,人均费用减少10元,直到达到75人为止.此次旅游旅行社需支付
各 种 费 用 共 计 1 5 0 0 0 元 .
(2)旅行团人数为多少时,旅行社可获得的利润最大
探究点三 分段函数模型
(1)写出每人需交费用y 关于x 的函数;
时
[ 解 ] ( ) 当 01 20 0 0 x,
润
(2) 设 旅 行 社 所 利 为 S 元 , 则 当 0< x≤ 7 5时 ,S= x (1 20 0 0 x) 5 0 00 =— 10x + 1 20 0 x— 150 0
当 30 — 0,
即
, 3 0< x 0 ≤7 5.
为 当 0数 ,
所 以 x =3 0 时 S max = 12 0 00 ;
当 30以 当 x =6 0 时 , 2 0 00 > 2 0 . 00
所 S ma x=
以 当 旅 行 团 人数 为 6 0 时 , 旅 行 社可 获 得 的 利 润 最 大 .
获
所
因
,
应用分段函数时的三个注意点 “段”一定要分得合理,不重不漏(关键词: “段”). 定义域为对应每一段自变量取值范围的并集(关键词 :
(1)分段函数的 (2)分段函数的
定义
域).
(3)分段函数的值域求法为: 域). 逐 段 求函数 值的范 围 , 最后再 结论(关 键词:
下
值
而
种
1. 某 工 3 厂6 年年 年 来生产某 产品 的 情况是 6年来 :前 这种 3年 产品 年 的 产 总 量的 产量 增 C 长 与 速 时 度 越 来
越 快 , 后
产量保 持不变 则该 厂 间t (年 )
的 函 数 关 系 图象 正确的 是( C )
C C
3 0 A 0 3 B 3 L C 3 t
D
[ 前 年 年 产量 的增长 速 度越 来 变 越 快 , 说明 呈 高 速 增 长 , 只 有 A , C 图
A
象 符 合 要 求 , 后 3 年 年 产 量 保 持不 , 故 选 A .]
(
3
0
,
A D
氧
随 着 下 的 含 氧 量 也
2. 海拔 高 升高 , 大 气 压强 降 ,空 气 随 之 下 降 ,
且 含 氧 量 , y(g 则 /m y与 )与 x 大 的 气 函 压 数 强 x 关系 (k 为 Pa) 成 正比 例 函 数 关 系 , 当 x = 36 kPa 时 , y =
0 8 g /m
( )
A. y = 3x (x ≥ 0) B. y =3x
D.
A [ 虑 由 到 题 含 意 氧 设 量 y = kx 能 (k 为 ≠ 负 0) , , 可 将( 知 36 x , ≥0 108) .] 代 入 解析 式可 得 k = 3 , 故 y =
,考
3x 不可
.某 人 定 制了 一 批 地 砖 , 每 块 地砖(如图所示)是边长为1
3
m 的 正 ,△ 方形 ABC D, 点 E,F 分 别 在 边 B C 和 C D 上 , 且 C E
=C F C E, F E,△A B 和 E和 四边 四边 形A 形 E A F EFD D的三 均由单一材料制成.制 种材料的每平方米价 F
成 △CF △ ABE
格 块 依 地 次 砖 为3所 0 需 元 的 、 材 20 料 元 费 、 用 1 最 0 省 元 问 : 点 E在什么位置时,每B
E C
[解 ] 设 CE = x m , 则 B E= ( - x)m , 每块 地 砖所 需 的 材 料费 用 为 W 元 ,
则
当 时 , W 有 最 小 值 , 即 费 用 最 省
故 当 点 E 与 点 C 相 距 0 .2 5 m 时 , 每 块 地 砖 所 需 的 材 料 费 用 最 省
3.4函数的应用(一)
例1 设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额
与3.1.2例8相同,全年综合所得收入额为(单位:元),应缴纳综合所得个
(1)求y 关于的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全
年应缴纳多少综合所得个税
税税额为 y(单位:元).
例 2一 辆 汽车 在 某 段路 程 中 行驶 的 平 均速 率v ( 单位 :km/ h) 与 时间t ( 单位 :h)
的 关 系 如 图 3.4 -1所示,
60
50
( 1 ) 求 图 3 .4-1 中阴影部 分的面积行 ,并 说明所 求面积的 实 际 含 义
(2)假设这 辆汽车 的里程表 在汽车 驶这段 路程前的 读 数为 2 004 km 试建 立
,
行 驶 这 段 路 程时 汽车里程 表读数s ( 单位:km ) 与时 t 的 函数 解析式 并画出 相
应的 图 象
,
90 80 70
40
30 20 10 O
图3.4 -1
[微 练 习 ]
市 场 营 销 人 员 的 个 人 月 收 入 与 其 每月 的销 量 成 一 次 函 数 关
1. 某 公 司
如 图 所 示 , 由 图 中 给 出 的 信 息 可 知 , 营销人 y 员没有销售量时的收 个收入/元 入 是 ( )
1300 x
800
l 2销售量/万件
0
A. 3 10 元 B. 3 00 元 C . 39 0 元 D. 2 80 元
B [ 由 图象 知 , , 当 该 =0 次 函 , 数 y 过 = ( 30 , 0.] 80 0) , (2 , 3 0 0) , 可 求 得 解 析 式 y =
50 0x + 30 0(x ≥ 0) x 时
系,
2. 若等腰 三角形的 周长为 2 0 , 底边长 y 是 关 于腰长x 的 函数 ,则它 的解
析式为(
—2x(x ≤ 0)
y = 20 —2x(5 ≤ x≤10 ) D . y= 2 0— 2 x(5 <
[由 题 意 ,得 2x y =2 0 , 所 以 y= 2 0— 2 x. 为 y> 0, 所 0 —2x >0,
所以 x< 10 .又 因为三 角 形 两 边 之 和 大 于 第三 边 ,所以
解 得 x> 5, 所 以 5< x< 10 . 故 选 D.]
因
+
A、B两地每台电脑的运费分别是40元、30元,乙地运往 A、B两地每台电脑
的运费分别是80元、50元.设甲地调运x 台电脑至B 地,该公司运往A 、B
两地的总运费为y 元 .
(1)求y 关于x 的函数关系式;
(2)若总运费不超过1000元,问有几种调运方案
(3)哪种方案总运费最低 并求出最低运费
探究点一 一次函数模型
[ 例 1] 某电脑公司在甲、乙两地各有一个分公司,甲地分公司现有电脑
6台,乙地分公司有同一型号的电脑12台.现A 地某单位向该公司购买该型
号的电脑10台,B 地某单位向该公司购买该型号的电脑8台. 已知甲地运往
地应 [解 调 ] 运( ( 8— ) x 甲 )台 地 电 调 运 x 至 台 B 电 地 脑 , 到 运 B 地 A , 地 则 剩 (8 下( — 6 x) —x ) 台 电 4) 运 脑 脑 台 到 ( A O≤ 地 , 乙
12—
脑 往 = (x + x ≤ 6,
x ∈ N) .
运
费 y = 30 x + 40 × (6 x ) + 50 × (8 x )+ 80 ×( x + 4) = 2 0x 十
9 60 (x ∈ N , 且 0 ≤x ≤ 6)
.
(2) 令 y ≤10 00 , 即 2 0x + 96 0 ≤ 0 00 , 得 x ≤ 2.
0≤ x ≤ 6, N
又 x∈ ,
∴0 ≤ x ≤2 , x ∈ N.
2 , 即 有 3 种 调 运 方 案
∴ x = 0 , , .
(3) ∵y 0≤ = x 2 0x + 96 0 N, 是 R 上 的 增 函 数 ,
又 ≤ 6, x ∈
∴当 x= 0 时 , y 有 最 小 值 9 6 0.
∴ 从 甲 地 运 6 台 到 A 地 , 从 乙 地 运 8 台 到 B 地 、 运 4 台到 A 地 , 此 时 运
费最 低 , 最 低 为 96 0
元 .
调
电
次 函 数 模 型 的 特 点 和 求 解 方 法
一
( ) 一 次 函 数 模 型 的 突 出 特 点 是 其 图象 是 一 条 直 线 .
(2 ) 解 一 次 函 数 模 型 时 , 注 意 待 定 系 数 法 的 应 用 , 主 要 步 骤 是 : 设 元 、 列
式 、 求 解 .
探究点二 二次函数模型
[例2] 某水果批发商销售进价为每箱40元的苹果,假设每箱售价不低于
50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每 天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元)之间的函数关系式;
(2)求该批发商平均每天的销售利润 w (元)与销售单价x(元)之间的函数关
系式;
(3)当每箱苹果的售价为多少元时,每天可以获得最大利润 最大利润是
多少
[ 解](1)根据题意,得y=90-3 (x—50),
化简得y=—3x+240(50≤x≤55,x∈N).
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利
润,所以w= (一3x+240)(x—40)=—3x +360x—9600(50≤x≤55,x∈N).
(3)因为w=—3x +360x—9600=-3(x—60) +1200,
所以当x<60 时 ,w 随 x 的增大而增大. 又50≤x≤55,x∈N,
所以当x=55 时 ,w 有最大值,最大值为1125.
所以当每箱苹果的售价为55元时,每天可以获得最大利润,最大利润是
1 1 2 5 元
二次函数模型的应用
根据实际问题建立二次函数模型后,可利用配方法、判别式法、换元法以
及函数的单调性等方法求最值,从而解决实际问题中的利润最大、用料最省等 最值问题.
[提醒] 利用二次函数求最值时,应特别注意取得最值时的自变量的值与
实际意义是否相符.
[例3] 国庆期间,某旅行社组团去风景区旅游,若旅行团人数为30人或
少于30人,则每人需交费用900元;若旅行团人数多于30人,则给予优惠: 每多1人,人均费用减少10元,直到达到75人为止.此次旅游旅行社需支付
各 种 费 用 共 计 1 5 0 0 0 元 .
(2)旅行团人数为多少时,旅行社可获得的利润最大
探究点三 分段函数模型
(1)写出每人需交费用y 关于x 的函数;
时
[ 解 ] ( ) 当 0
润
(2) 设 旅 行 社 所 利 为 S 元 , 则 当 0
当 30 — 0,
即
, 3 0< x 0 ≤7 5.
为 当 0
所 以 x =3 0 时 S max = 12 0 00 ;
当 30
所 S ma x=
以 当 旅 行 团 人数 为 6 0 时 , 旅 行 社可 获 得 的 利 润 最 大 .
获
所
因
,
应用分段函数时的三个注意点 “段”一定要分得合理,不重不漏(关键词: “段”). 定义域为对应每一段自变量取值范围的并集(关键词 :
(1)分段函数的 (2)分段函数的
定义
域).
(3)分段函数的值域求法为: 域). 逐 段 求函数 值的范 围 , 最后再 结论(关 键词:
下
值
而
种
1. 某 工 3 厂6 年年 年 来生产某 产品 的 情况是 6年来 :前 这种 3年 产品 年 的 产 总 量的 产量 增 C 长 与 速 时 度 越 来
越 快 , 后
产量保 持不变 则该 厂 间t (年 )
的 函 数 关 系 图象 正确的 是( C )
C C
3 0 A 0 3 B 3 L C 3 t
D
[ 前 年 年 产量 的增长 速 度越 来 变 越 快 , 说明 呈 高 速 增 长 , 只 有 A , C 图
A
象 符 合 要 求 , 后 3 年 年 产 量 保 持不 , 故 选 A .]
(
3
0
,
A D
氧
随 着 下 的 含 氧 量 也
2. 海拔 高 升高 , 大 气 压强 降 ,空 气 随 之 下 降 ,
且 含 氧 量 , y(g 则 /m y与 )与 x 大 的 气 函 压 数 强 x 关系 (k 为 Pa) 成 正比 例 函 数 关 系 , 当 x = 36 kPa 时 , y =
0 8 g /m
( )
A. y = 3x (x ≥ 0) B. y =3x
D.
A [ 虑 由 到 题 含 意 氧 设 量 y = kx 能 (k 为 ≠ 负 0) , , 可 将( 知 36 x , ≥0 108) .] 代 入 解析 式可 得 k = 3 , 故 y =
,考
3x 不可
.某 人 定 制了 一 批 地 砖 , 每 块 地砖(如图所示)是边长为1
3
m 的 正 ,△ 方形 ABC D, 点 E,F 分 别 在 边 B C 和 C D 上 , 且 C E
=C F C E, F E,△A B 和 E和 四边 四边 形A 形 E A F EFD D的三 均由单一材料制成.制 种材料的每平方米价 F
成 △CF △ ABE
格 块 依 地 次 砖 为3所 0 需 元 的 、 材 20 料 元 费 、 用 1 最 0 省 元 问 : 点 E在什么位置时,每B
E C
[解 ] 设 CE = x m , 则 B E= ( - x)m , 每块 地 砖所 需 的 材 料费 用 为 W 元 ,
则
当 时 , W 有 最 小 值 , 即 费 用 最 省
故 当 点 E 与 点 C 相 距 0 .2 5 m 时 , 每 块 地 砖 所 需 的 材 料 费 用 最 省
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
