3.2单调性 课件(共29张PPT)-高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.2单调性 课件(共29张PPT)-高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 16:49:02 | ||
图片预览






文档简介
(共29张PPT)
第3章函数的概念与性质
3.2.1 函数的单调性
03. 分段函数图象应用
分段图象
01. 分段函数求值
目录
学习目标
1.理解函数的单调性及其几何意义,能运用函数图象理解
和研究函数的单调性.
2.会用函数单调性的定义判断(或证明)一些函数的单调性.
3.会求一些具体函数的单调区间.
Topic.01
01 情景导入
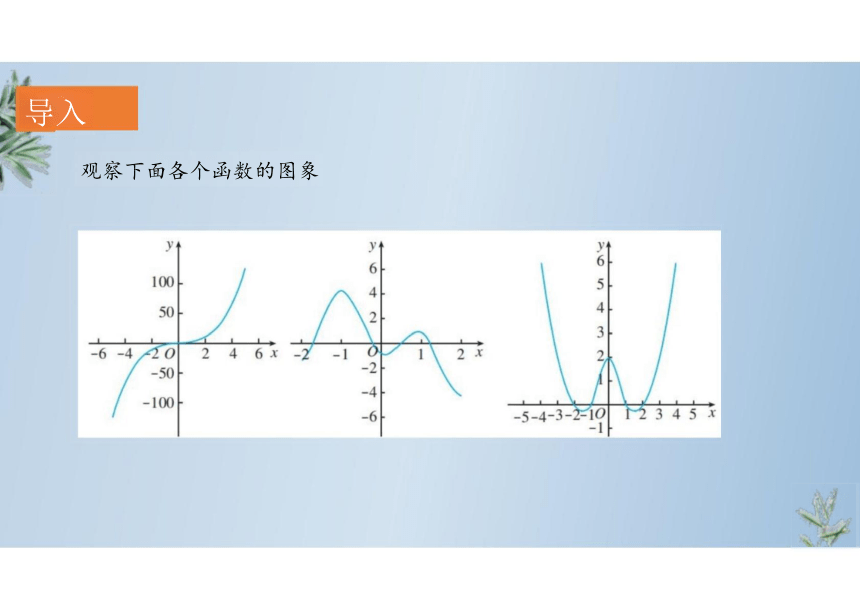
导入
观察下面各个函数的图象
问题1:函数图象都有什么特征
图一为上升趋势,图二、图三有上升也有下降趋势.
问题2:反映了函数的哪些性质
函数值随着自变量的增大而增大(或减小)的性质,即反映了
函数图 象的单调性。
Topic.02
02 函数的单调性
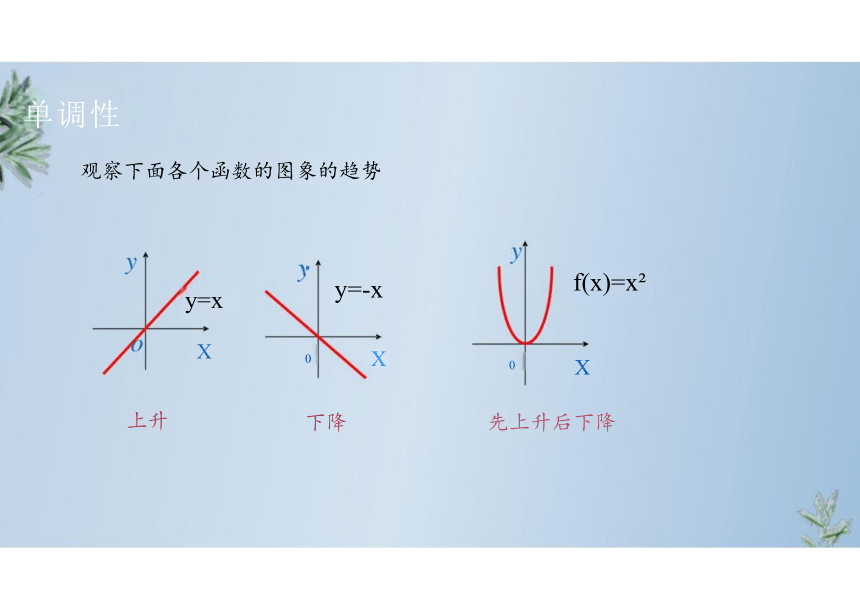
单调性
观察下面各个函数的图象的趋势
f(x)=x
0 X
先上升后下降
y=-x
0 X
下降
y=x
X
上升
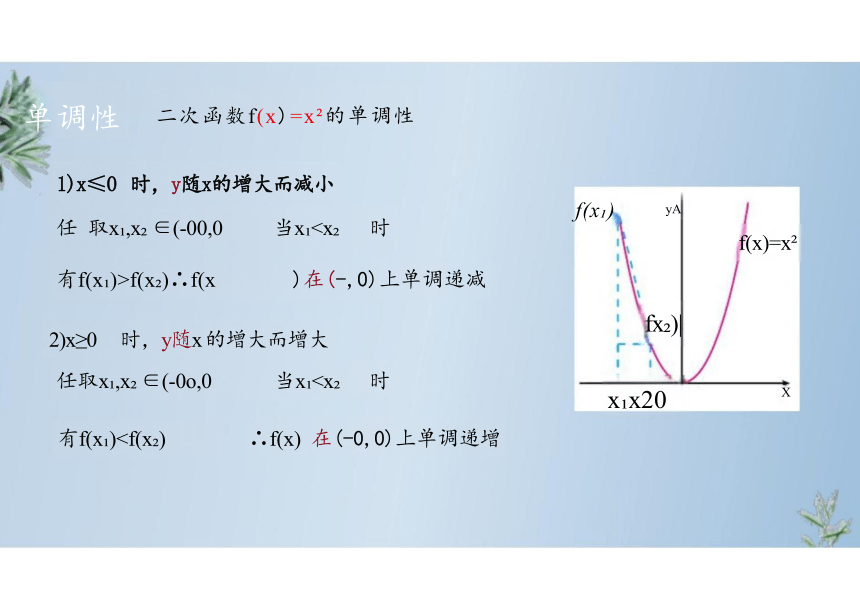
单调性 二次函数f(x)=x 的单调性
1)x≤0 时,y随x的增大而减小
任 取x ,x ∈(-00,0 当x有f(x )>f(x )∴f(x )在(-,0)上单调递减
2)x≥0 时,y随x 的增大而增大
任取x ,x ∈(-0o,0 当x有f(x )f(x ) yA
fx )|
x x20
f(x)=x
X
单调性
函数f(x) 的定义域I, 区 间DEI, 在区间D 上的任意两个自变量的值x ,x
y 个 y=f(x)
增函数 Vx ,X ∈D, 当x那么就称函数f(x) 在区间D上单调递增。 0 x x x
x
x
f
f
Vx ,X ∈D, 当xf(x ),
那么就称函数f(x)在区间D 上单调递减
y=f(x)
x x x
y
f(x,) f(x )
0
减函数
函数单调性定义的等价形式(对于任意的x ,x ∈A 且x ≠x ):
一 f(x) 在D 上为增函数;
f(x) 在D上为减函数;
(3)(x -x )(f(x )-f(x ))>0 f(x) 在 D上为增函数;
(4)(x -x )(f(x )-f(x ))<0 f(x) 在D 上为减函数.
一
思考1:函 数f(x)在定义域的某区间上存在x ,X 满足x且f(x )不一定是增函数,如右图
思考2:函数的单调性是对定义域内某个区间而言的,
(1)你能举出在整个定义域内是单调递增的函数例子吗
(2)你能举出在定义域内的某些区间单调递增但在另一些区间上单
调递减的函数例子吗
(1)定义域内是单调递增的函数
f(x)=2x+4
(2)某些区间单调递增但在另一些区间上单调
递减如右图
Topic.03
03 函数单调性的证明
证明单调性
判断(证明)单调性:
→单调递增
单调递减
xf(x )→
x证明单调性
1.根据定义,研究函数f(x)=kx+b(k≠0) 的单调性
解:函数 f(x)=kx+b(k≠0) 的定义域是R, 对于任意的x ,x ∈R 且x都有f(x )-f(x )=(kx +b)-(kx +b)=k(x -x )
由 x < x 知 x -x < 0 ,
当 k>0 时,f(x )-f(x )<0 ,即 f(x )这时,函数 f(x)=kx+b(k≠0) 是增函数;
当k<0 时 ,k(x -x )>0 ,即 f(x )-f(x )>0 ,f(x )>f(x )
这时,函数 f(x)=kx+b(k≠0) 是减函数;
证明单调性
用定义证明函数的单调性的步骤:
1. 取数:任取x ,x ∈D, 且x2. 作差:f(x )一f(x );
3.变形:通常是因式分解和配方;
4.定号:判断差f(x )一f(x )的正负;
5.结论:指出函数f(x)在给定的区间D 上的单调性.
证明单调性
2.利用单调性的定义判断函数
变形
∵-10,xi+1>0,x +1>0.
,即fx)-fx )>0.fx) >x ).
(-1,+)上单调递减.
Vxi,x ∈(-1,+0),设xi则f(x )-f(x )
取值
作差
定号
结论
(-1,+0)上的单调性.
· ·
··
Topic.04
04 函数单调性应用
求单调区间
1.f(x)的图像如士所示,则函数f(x)的单调递减区 间是 ( D )
A.(-1,0) B.(1,+00)
C.(-1,0)U(1,+oo) D.(-1,0),(1,+oo)
YA
3
2
-3/ -2-1 01
0 2 4 6
-2
2.函数f(x)=x -2x-3的单调增区间是 [1,+oo]
[变式]函数f(x)=kx -2x-3|的单调增区间是 I-1,1]和(3,+oo)
3函数f(x)=-x +2kx|+1的单调减区间是 I -1,01和(1,+oo).
求单调区间
2 3 X
0
作出函数 的图象,如图所示
函数f(x)的单调递减区间为(-00,1)和[1,2];单调递增区间为(2,+0).
y个
-20
-3 -1 2 x
求单调区间
3.作出函数
的图象,并指出函数的单调区间.
求单调区间
注意:
(1)函数在某个区间上单调递增(减),但是在整个定义域上不一定都是单调递增(减).如函数
0)在区间(-0,0)和(0,+0)上都单调递减,但是在整个定义域上不具有单调性.
(2)当一个函数出现两个或两个以上的单调区间时,不能用“U” 连接,而应该用“ 和”或 “,”连
接.如函数 在区间(-~,0)和(O,+一上都单调递减,不能认为 的单调递减区间为(-
0,0)U(0,+0).
思考:试判 的单调性
①增+增=增 y=x +2x,x∈R
②减+减=减
,xe(0,+co)
④减一增=减 ,xe(,+o)
注:“增一增”、“减一减”无法确定单调性
求单调区间
③增一减=增
4.( 多选题)下列函数在(-o,0) 上单调递增的是(CD).
Ixl x2 X
求单调区间
由题意知函数fx) 是定义在(-1,1)上的减函数,
又fm -1)102
故实数m 的取值范围是(1,2).
所以
应用
1.已知函数fx) 的定义域为R, 且对于Vx1,x ∈(-1,1), 都
fm-1)因为函数fx) 的定义域为R, 且对于Vx,x ∈R, 都 ,所以函数
则不等式(×1)><2-)
所以不等式的解集为
2.已知函数fx) 的定义域为R,且对于Vx ,x ∈R,都
由fx-1)>f2-x), 得x-1>2-x, 解 得
f(x)在定义域R 上单调递增.
的解集为
Topic.05
05 课堂小结
课堂小结
总结:
1.函数单调性定义。
2.函数单调性证明
3 .函数单调性的应用
第3章函数的概念与性质
3.2.1 函数的单调性
03. 分段函数图象应用
分段图象
01. 分段函数求值
目录
学习目标
1.理解函数的单调性及其几何意义,能运用函数图象理解
和研究函数的单调性.
2.会用函数单调性的定义判断(或证明)一些函数的单调性.
3.会求一些具体函数的单调区间.
Topic.01
01 情景导入
导入
观察下面各个函数的图象
问题1:函数图象都有什么特征
图一为上升趋势,图二、图三有上升也有下降趋势.
问题2:反映了函数的哪些性质
函数值随着自变量的增大而增大(或减小)的性质,即反映了
函数图 象的单调性。
Topic.02
02 函数的单调性
单调性
观察下面各个函数的图象的趋势
f(x)=x
0 X
先上升后下降
y=-x
0 X
下降
y=x
X
上升
单调性 二次函数f(x)=x 的单调性
1)x≤0 时,y随x的增大而减小
任 取x ,x ∈(-00,0 当x
2)x≥0 时,y随x 的增大而增大
任取x ,x ∈(-0o,0 当x
fx )|
x x20
f(x)=x
X
单调性
函数f(x) 的定义域I, 区 间DEI, 在区间D 上的任意两个自变量的值x ,x
y 个 y=f(x)
增函数 Vx ,X ∈D, 当x
x
x
f
f
Vx ,X ∈D, 当x
那么就称函数f(x)在区间D 上单调递减
y=f(x)
x x x
y
f(x,) f(x )
0
减函数
函数单调性定义的等价形式(对于任意的x ,x ∈A 且x ≠x ):
一 f(x) 在D 上为增函数;
f(x) 在D上为减函数;
(3)(x -x )(f(x )-f(x ))>0 f(x) 在 D上为增函数;
(4)(x -x )(f(x )-f(x ))<0 f(x) 在D 上为减函数.
一
思考1:函 数f(x)在定义域的某区间上存在x ,X 满足x
思考2:函数的单调性是对定义域内某个区间而言的,
(1)你能举出在整个定义域内是单调递增的函数例子吗
(2)你能举出在定义域内的某些区间单调递增但在另一些区间上单
调递减的函数例子吗
(1)定义域内是单调递增的函数
f(x)=2x+4
(2)某些区间单调递增但在另一些区间上单调
递减如右图
Topic.03
03 函数单调性的证明
证明单调性
判断(证明)单调性:
→单调递增
单调递减
x
x
1.根据定义,研究函数f(x)=kx+b(k≠0) 的单调性
解:函数 f(x)=kx+b(k≠0) 的定义域是R, 对于任意的x ,x ∈R 且x
由 x < x 知 x -x < 0 ,
当 k>0 时,f(x )-f(x )<0 ,即 f(x )
当k<0 时 ,k(x -x )>0 ,即 f(x )-f(x )>0 ,f(x )>f(x )
这时,函数 f(x)=kx+b(k≠0) 是减函数;
证明单调性
用定义证明函数的单调性的步骤:
1. 取数:任取x ,x ∈D, 且x
3.变形:通常是因式分解和配方;
4.定号:判断差f(x )一f(x )的正负;
5.结论:指出函数f(x)在给定的区间D 上的单调性.
证明单调性
2.利用单调性的定义判断函数
变形
∵-1
,即fx)-fx )>0.fx) >x ).
(-1,+)上单调递减.
Vxi,x ∈(-1,+0),设xi
取值
作差
定号
结论
(-1,+0)上的单调性.
· ·
··
Topic.04
04 函数单调性应用
求单调区间
1.f(x)的图像如士所示,则函数f(x)的单调递减区 间是 ( D )
A.(-1,0) B.(1,+00)
C.(-1,0)U(1,+oo) D.(-1,0),(1,+oo)
YA
3
2
-3/ -2-1 01
0 2 4 6
-2
2.函数f(x)=x -2x-3的单调增区间是 [1,+oo]
[变式]函数f(x)=kx -2x-3|的单调增区间是 I-1,1]和(3,+oo)
3函数f(x)=-x +2kx|+1的单调减区间是 I -1,01和(1,+oo).
求单调区间
2 3 X
0
作出函数 的图象,如图所示
函数f(x)的单调递减区间为(-00,1)和[1,2];单调递增区间为(2,+0).
y个
-20
-3 -1 2 x
求单调区间
3.作出函数
的图象,并指出函数的单调区间.
求单调区间
注意:
(1)函数在某个区间上单调递增(减),但是在整个定义域上不一定都是单调递增(减).如函数
0)在区间(-0,0)和(0,+0)上都单调递减,但是在整个定义域上不具有单调性.
(2)当一个函数出现两个或两个以上的单调区间时,不能用“U” 连接,而应该用“ 和”或 “,”连
接.如函数 在区间(-~,0)和(O,+一上都单调递减,不能认为 的单调递减区间为(-
0,0)U(0,+0).
思考:试判 的单调性
①增+增=增 y=x +2x,x∈R
②减+减=减
,xe(0,+co)
④减一增=减 ,xe(,+o)
注:“增一增”、“减一减”无法确定单调性
求单调区间
③增一减=增
4.( 多选题)下列函数在(-o,0) 上单调递增的是(CD).
Ixl x2 X
求单调区间
由题意知函数fx) 是定义在(-1,1)上的减函数,
又fm -1)
故实数m 的取值范围是(1,2).
所以
应用
1.已知函数fx) 的定义域为R, 且对于Vx1,x ∈(-1,1), 都
fm-1)
则不等式(×1)><2-)
所以不等式的解集为
2.已知函数fx) 的定义域为R,且对于Vx ,x ∈R,都
由fx-1)>f2-x), 得x-1>2-x, 解 得
f(x)在定义域R 上单调递增.
的解集为
Topic.05
05 课堂小结
课堂小结
总结:
1.函数单调性定义。
2.函数单调性证明
3 .函数单调性的应用
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
