中考复习-系统性工程

课件26张PPT。中考复习：系统性的工程团结就是力量！ 每一个老师所取得的每一次成果，都是我们全数学级集体力量的体现，是我们集体智慧的结晶。
对于中考复习，我们也是一直以来坚持群策群力，分工合作。第一轮复习前即进行版块分工，进行知识点归纳，基本技能归纳，题型归纳。第二轮复习前进行版块题型预测，以及知识点交叉可能性交流。 一、情感教育：关注每一个学生二、知识点把握：第一轮复习把书读厚，第二轮复习把书读薄。三、课堂教学：向45分钟要效率 中考是每一个学生参与的比赛，中考成绩也离不开每一个同学的积极努力。复习阶段压力大，有一部份学生，尤其是学困生容易心理失衡，从而导致学习没有积极性，甚至产生自暴自弃心理。只有细心关注学生情绪变化，关心学生身体健康，生活习惯，才能与学生同甘共苦，共创佳绩。 一、情感教育：关注每一个学生针对性措施：分层教学，制定个性化目标。 （1）第一轮复习抓双基：基础知识，基本技能；关注知识的外延，把书读厚。（2）第二轮复习抓思想方法，以思想方法为纲，做到纲举目张；关注知识的内涵，把书读薄。
二、知识点把握：第一轮复习把书读厚，第二轮复习把书读薄。浙江杭州2008小张根据某媒体上报道的一张条形统计图（如右），在随笔中写道：“……今年在我市的中学生艺术节上，参加合唱比赛的人数比去年激增……”。小张说得对不对？为什么？请你用一句话对小张的说法作个评价：
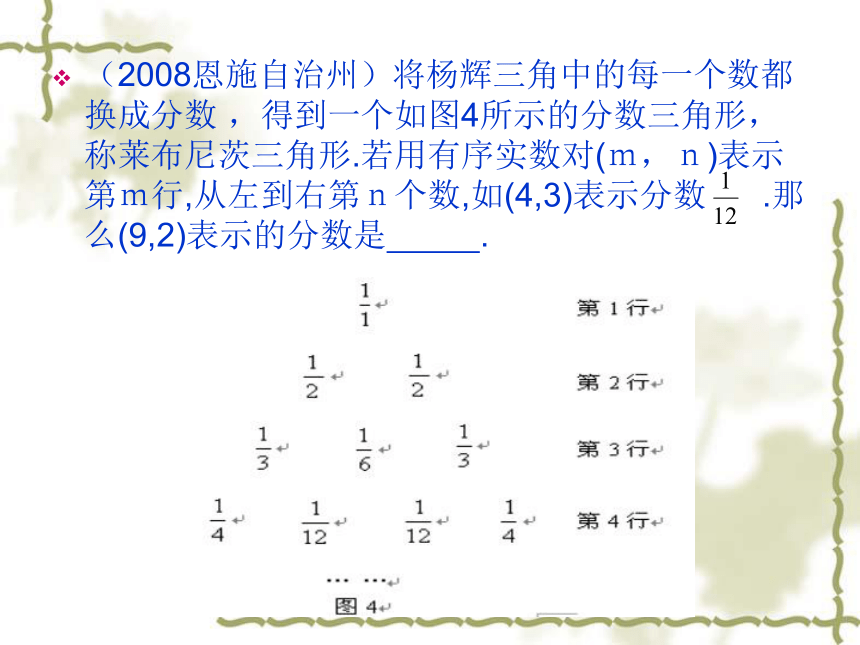
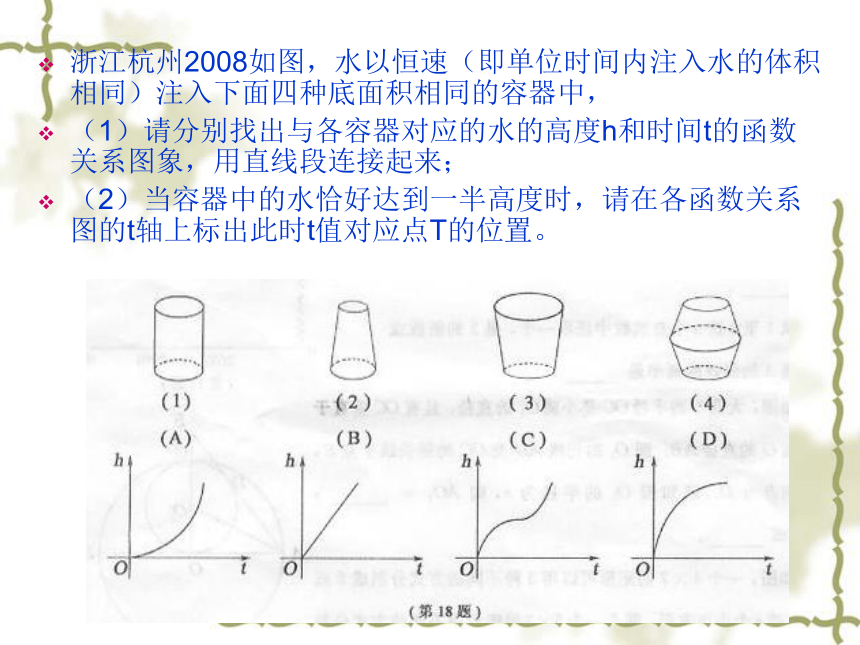
______________________________________（2008恩施自治州）将杨辉三角中的每一个数都换成分数 ，得到一个如图4所示的分数三角形，称莱布尼茨三角形.若用有序实数对(ｍ，ｎ)表示第ｍ行,从左到右第ｎ个数,如(4,3)表示分数 .那么(9,2)表示的分数是 . 数学思想方法是数学的灵魂。数学教材编写及教学始终反映着两条线，即数学基础知识和数学思想方法，数学知识以显性形式展示，而数学思想方法则以隐性形式存在，它们交相辉映，构建了生机勃勃的数学知识、思想、方法体系.初中数学中常用的思想方法有：①数学方法：配方法、换元法、待定系数法、消元法等； ②数学逻辑方法：分析法、综合法等； ③数学思维方法：分析与综合、特殊与一般、类比、归纳和演绎等；④数学思想：函数与方程思想、数形结合思想、分类讨论思想、转化（化归）思想等. 浙江杭州2008如图，水以恒速（即单位时间内注入水的体积相同）注入下面四种底面积相同的容器中，
（1）请分别找出与各容器对应的水的高度h和时间t的函数关系图象，用直线段连接起来；
（2）当容器中的水恰好达到一半高度时，请在各函数关系图的t轴上标出此时t值对应点T的位置。浙江金华2008如图，第（1）个多边形由正三角形“扩展”而来，边数记为a3，第（2）个多边形由正方形“扩展”而来，边数记为a4，…，依此类推,由正边形“扩展”而来的多边形的边数记为（n≥3）.则 a5 的值是 ▲ ,当 的结果是197/600时，n的值 ▲ . （福建福州2008）如图，在反比例函数y=2/x（x>0）的图象上，有点P1,P2,P3,P4，它们的横坐标依次为1，2，3，4．分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1,S2,S3，则S1+S2+S3= ． 教学的主要阵地是课堂，只有切实提高课堂教学的效率，才能使学生快乐学习，学得轻松，学得有效果。三、课堂教学：向45分钟要效率功夫在课外：
备课充分一点，课堂效率就高一点；
教师多做一点，学生效果就好一点；
练习精练一点，学生压力就小一点。1、请研究二次函数y=x2+4x+3的图象及其性质，并尽可能多地写出有关结论。 解（1）图象的开口方向:
（2）顶点坐标：
（3）对称轴：
（4）图象与x轴的交点为：
（5）图象与y轴的交点为：
（6）图象与y轴的交点关于
对称轴的对称点坐标为：
（7）最大值或最小值：
（8）y的正负性：
（9）图象的平移：
（10）图象在x轴上截得的线段长（11）对称抛物线.　串“知识点” 1、某海滨浴场的沿岸可以看作直线，如图所示，1号救生员在岸边的A点看到海中的B点有人求救，便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助；若每位救生员在岸上 跑步的速度都是6米/秒，在水中游泳的速度都是2米/秒。 1. 请问1号救生员的做法是否合理？ 2. 若2号救生员从A 跑到D再跳入海中游到B点救助,请问谁先到达B？　串“典型图形” 2、如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB＝45°,量得BC长为100米,求河的宽度（即求BC边上的高）.3、外国船只，除特许外，不得进入我国海洋100海里以内的
区域。如图，设A、B是我们的观察站，A和B之间的距离为
160海里，海岸线是过A、B的一条直线。一外国船只在P点，
在A点测得∠BAP=450，同时在B点测得∠ABP=600，问此时
是否要向外国船只发出警告，令其退出我国海域.
┓C
问题1：楼房AB的高度是多少?问题2：楼房CD的高度是多少?5、为打捞一失事飞机上的黑匣子，潜水员在A处以每小时8海里的速度向正东方向划行，在A处测得黑匣子B在北偏东60度的方向，半小时后到达C处，测得B在北偏东30度的方向，问潜水员继续向东划行时,距B的最近距离是多少?（精确到0.1m)ADCB北北30゜60゜？EF 如图，长方形ABCD中有一个小正方形AEFG，点E、G分别在AB、AD上，点F在正方形ABCD的内部，试说明线段BE与DG之间的关系. BE⊥DGBE=DGEGFM 一图多变 一图多变BE⊥DGBE=DGABCDEGABCDEGABCDEGABCDEGFFFGABCDEFGABCDEFGHPQR 一图多变（08福建南平26题） （1）如图1，图2，图3，在 中，分别以为边，向外作正三角形，正四边形，正五边形，相交于点O．①如图1，求证： ；
②探究：如图1， ；
如图2， ；
如图3， ．
（2）如图4，已知：AB,AD是以AB为边向外所作正n边形的一组邻边；AC,AE是以AC为边向外所作正n边形的一组邻边．BE,CD的延长相交于点O．
①猜想：如图4，∠BOC （用含n的式子表示）；
②根据图4证明你的猜想． （08义乌）如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka， CG=kb (a≠b，k＞0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（3）在第(2)题图5中，连结DG、BE，且a=3，b=2，
k= ，求 的值．多一些指导，少一些灌输；
多一些讨论，少一些讲解；
多一些归纳，少一些重复；
多一些学趣，少一些压力 。